基于改进残差网络的雷达辐射源信号识别

郭恩泽，张洪德*，杨 雷，刘益岑，彭镜轩，张 磊

(1.中国人民解放军陆军工程大学 通信士官学校，重庆 400035；2.中国人民解放军陆军工程大学 通信工程学院，江苏 南京 210007；3.信号盲处理国家级重点实验室，四川 成都 610041)

0 引言

雷达辐射源识别是实施雷达对抗的前提和基础，是在雷达信号截获、分选的基础上，通过分析雷达信号的工作参数和特征参数，利用这些参数推断该雷达的体制、用途、型号、威胁等级和部署地点等信息，为己方进行电子对抗决策提供重要的情报支撑，其识别水平是衡量雷达对抗设备技术先进程度的重要标志[1]。随着电磁环境的信号日趋密集、雷达体制的多样化及普遍存在的噪声等影响，传统的参数匹配法[2]和通过将信号进行时域[3]、频域和时频域[4]等变换，然后人工提取脉内特征进行分类识别的方法，存在低信噪比下识别率低[5]、泛化能力弱[6]和鲁棒性差等缺点。

当前，深度学习方法在图像分类[7]、计算机视觉[8]和语音识别[9]等方面取得了瞩目的成绩，国内外学者逐渐开始利用深度学习的方法进行雷达辐射源识别的研究[10]。其中，典型的深度学习模型是卷积神经网络(Convolutional Neural Network，CNN)，利用CNN在解决计算机视觉任务上的强大性能，对雷达辐射源信号进行一定的变换，提取其二维图像特征(较为常用的是时频分布特征)作为样本训练CNN模型，然后进行分类识别[11]。文献[12]首先将雷达信号变换为雷达时频图像，然后利用设计的CNN对时频图进行分类识别，在信噪比为-8 dB条件下，对8种雷达信号的识别率可以达到98.31%。相比于结构简单的的网络模型，AlexNet[13]，VGGNet[14]，GoogLeNet[15]等网络模型有着高效的结构设计、提取更多特征的深层结构及成熟的性能，在ImageNet比赛中均取得了优秀的成绩。部分学者开始利用这些网络模型进行雷达时频图像识别，文献[16-18]利用AlexNet模型对雷达辐射源信号、雷达干扰信号和低截获概率雷达信号进行分类识别，取得了良好的识别率，比采用非深度学习的分类方法和利用LeNet5 CNN模型分类的方法识别效果更好、抗噪性能更强。文献[19]利用VGGNet模型对5种雷达辐射源信号进行分类识别，在信噪比为-12 dB的噪声条件下，识别率达到90%。文献[20]利用GoogLeNet的预训练模型对窄带雷达群目标进行识别，在小样本条件下取得了较高的识别率。近年来，为了提高识别速度，方便网络模型在便携设备上应用，轻量级神经网络以其高效的网络计算方式成为研究的热点[21]，2016年—2019年，轻量化的CNN SqueezeNet，MobileNetV2[22]等模型相继被提出。文献[23]设计了轻量级神经网络对8种电磁调制信号进行识别，在信噪比为-6～6 dB的噪声条件下获得96.1%的综合识别率。

上述方法从不同的角度进行了探索，其主要研究不足在于：为了提取更为复杂的目标特征，上述网络模型都有着较深的网络层数和较大的参数量，不可避免地带来了梯度传播时的消失或者爆炸现象，会导致网络误差不断增大，网络的识别正确率出现饱和甚至是下降的现象。残差网络通过在前向神经网络上增加一个跳跃从而绕过一些网络层，实现快捷连接，解决了以上问题。因此，本文在分析雷达信号时频图特性的基础上，借鉴轻量化[21-23]和图像识别相关研究[24]的网络设计思想，设计一种以残差网络为主体结构[25]的改进残差网络模型，该模型兼顾了性能和复杂度。

1 雷达信号模型与时频分析处理

在高斯白噪声环境下，侦察接收机接收雷达信号的模型可表示为：

x(t)=s(t)+n(t)，

(1)

式中，s(t)为雷达信号；n(t)为高斯白噪声。

雷达信号s(t)又可以表示为：

s(t)=Ae{j[2πf0 t+φ(t)+φ]}，

(2)

式中，A为辐射源幅度；f0为辐射源信号载频；φ为初始相位；φ(t)为脉内调制信息。辐射源的特征差异集中体现在φ(t)，本文主要考虑7种调制方式:常规脉冲信号(CW)、线性调频信号(LFM)、非线性调频信号(NLFM)、二相编码信号(BPSK)、四相编码信号(QPSK)、二相频率编码信号(BFSK)以及四相频率编码信号(QFSK)。

传统的信号处理中，主要是在时域和频域分析信号。信号的时域表示信号随时间的变化关系，信号的频域表示信号在整个时间内的全部频谱成分。因此，时域和频域分析并不能揭示频率随时间的变化关系。时频分析能够同时在时域和频域描述信号，将一维的时域信号转化为二维的时间和频率密度函数，揭示了信号能量随时间和频率的变化关系，有助于在信号识别时提取更多的信号特征。本文利用短时傅里叶变换(STFT)作为时频分析的方法，给定一个信号s(t)，其短时傅里叶变换可定义为：

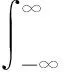
(3)

式中，h(t)为加窗函数。可以看出，变换域同时涵盖了时间和频率的调制信息，而且可以利用深度CNN对图像识别的强大功能处理二维时频图。

信噪比为0 dB时，7类雷达信号的时频分布图像图如图1所示。可以看出，BPSK，CW，LFM能量分布比较特殊，与其他信号差异明显，而其他4种信号时频图像特征在一定程度上被噪声“淹没”，尤其对于相似度较高的BFSK，QFSK信号，当信噪比较低时，识别容易产生混淆。

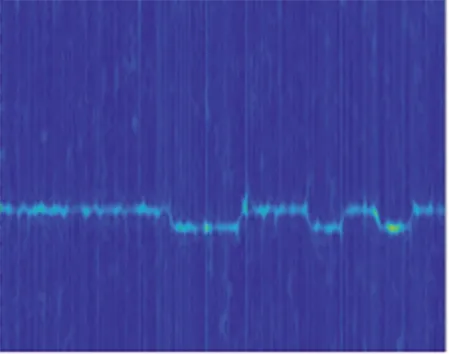
(a) BFSK

(b) BPSK

(c) CW

(d) LFM

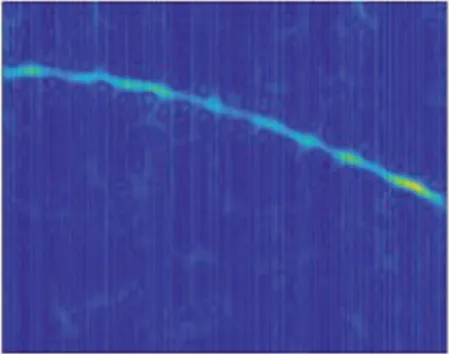
(e) NLFM

(f) QFSK

(g) QPSK图1 7类雷达信号的STFT时频分布Fig.1 STFT time-frequency distribution of seven types of radar signals

2 基于改进残差网络的雷达辐射源识别

2.1 CNN训练理论推导

CNN的训练过程是构建代价函数，通过学习来找到最合适的权重和偏置，使得代价函数接近最小值。其中，梯度下降法是该过程的核心，梯度就是函数上升最快的方向，要使代价函数下降最快，应沿着梯度的反方向[26]。

假设输出类别为N，第i个输出可表示为卷积核的权重w和卷积核的偏置b的函数zi(w,b)，经过激活函数f后的输出ai(w,b)可表示为:

ai(w,b)=f(zi(w,b))。

(4)

假设各学习数据输出对应的正确解为ti，总共有M个训练样本,则第k个训练样本图像的平方误差函数Ck可表示为：

(5)

利用全体训练样本的平方误差总和构建代价函数C：

(6)

根据代价函数，梯度下降法的数学表示为：

(7)

在误差反向传播算法中引入神经元输出误差δi的概念，δi可表示为：

δi=(ai-ti)f′(zi)。

(8)

根据δi可以求出：

(9)

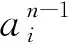
由式(7)～式(9)可知，仅需要计算出输出层的神经元误差，然后通过将误差一层一层反向传播，可以计算出其他神经元误差，进而计算出下降梯度，更新网络模型中的参数值。误差反向传播算法确定CNN参数的流程如图2所示。

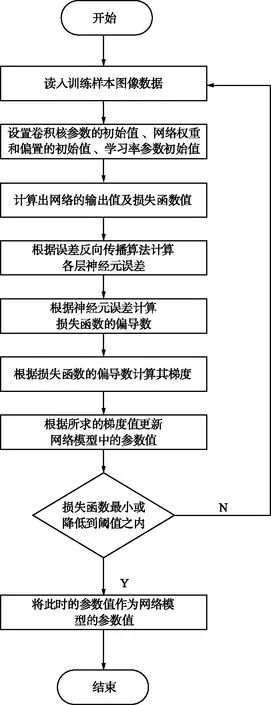
图2 误差反向传播算法确定CNN参数的流程Fig.2 Flow chart of error backpropagation algorithm to determine parameters of CNN

2.2 残差网络原理

自AlexNet之后，CNN层数不断加深，网络拟合能力越来越强，但网络的识别率却趋于饱和，甚至有下降的趋势，训练误差也不再减小。分析原因：一是由于深度网络不易优化，有效信息难以被直接利用；二是由于反向传播的梯度计算是在上一层基础上进行的，网络深度加深会使梯度复乘，使梯度在多层反向传播时越来越小，最终导致梯度消失。

残差网络基于残差结构的设计，实现快捷连接(Shortcut Connection)，解决了以上问题。残差网络模块如图3所示，假设CNN某一层输入为X，在经过网络传输处理之后，得到的期望输出为H(X)。残差模块的引入改变了网络学习目标，使其不再学习一个完整的输出H(X)，而是学习输出与输入之间的差别，即残差F(X)：

F(X)=H(X)-X。

(10)

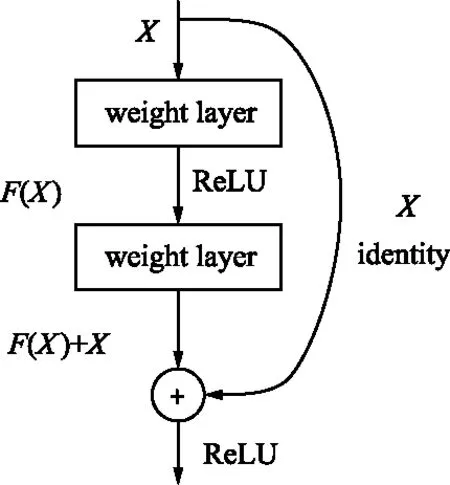
图3 残差网络模块Fig.3 Residual network module

当网络达到某一个深度时，如果网络的训练已经达到最优状态，此时的错误率最低，再往下加深，网络会出现退化问题。此时,X就是最优输入，接下来仅需要建立恒等快捷映射(H(X)等于X)，令F(X)等于0即可，这样网络深度增加，训练误差也不再上升。

当上下2层的通道数不一致时，即输出F(X)与X维度不一致，可以在做快捷连接时，对X做一定的线性变换，此时H(X)可表示为：

H(X)=F(X)+W*X，

(11)

式中，W为卷积操作，在实际模型中，通常用1×1的卷积核进行升维或者降维操作，以便和F(X)保持维度一致。

2.3 改进残差网络模型设计

2.3.1 改进残差网络模型设计方法描述

残差网络由于其独特的快捷连接设计，在一定程度上保证了信息的完整性，解决了传统卷积在信息传递时出现的信息丢失和损耗问题，避免了由于网络过深导致的性能下降问题，进一步提高了对目标的分类识别率。因此，本文选择残差结构为主体，设计适合雷达信号识别的深度学习网络模型。

目前，残差网络模型共有5种不同的深度，分别是：ResNet18，ResNet34，ResNet50，ResNet101，ResNet152，模型后面的数字代表残差模型的网络深度。有研究表明，残差网络的效果类似于不同深度网络模型的集成。因此，在一定程度上，随着残差网络模型的深度增加，其性能也越来越好。然而，上述模型在追求性能的同时，模型规模和计算量也成倍增长，很难取得性能与复杂度的双重提升。深入分析发现，由于残差结构的优越性，残差网络深度相对较浅时，随着模型深度的增加，模型性能提升幅度较大，当模型深度达到一定程度之后，再增加深度，模型性能提升幅度较小，并逐渐趋近于饱和。例如，文献[25]利用ImageNet数据集对上述残差模型进行训练和测试，结果表明，34层的残差模型比18层的残差模型错误率低3.3%；50层的残差模型比34层的残差模型错误率低1.7%；152层的残差模型比50层的残差模型错误率低1.4%。因此，需要根据所要识别目标，设计合适的残差模型深度，平衡模型性能和复杂度。

雷达辐射源信号时频图不同于实际生活中的图像数据，与真实图像相比，细微特征不够丰富、表达特征的信息相对较少、图像质量较差，而目前的残差网络模型主要针对真实图像设计。因此，需要根据雷达信号时频图的特点，选择合适的残差模型体量以及输出维度。

与此同时，文献[24]对残差网络进行深入研究，通过可视化分析和实验结果发现，最大池化层(Maxpoling)会导致高幅度高频率的激活值，增加网格(Gridding)效应。为了进一步提升网络模型性能，使用卷积层替代最大池化层。本文设计改进残差网络模型也借用这一设计思想。

2.3.2 改进残差网络模型框架

综上分析，本文设计了一种改进的残差网络模型，采用文献[25]提出的残差网络主干结构，与文献[25]模型框架对比如表1所示。由5个卷积部分、一个最大池化层、一个全局平均池化层(Average Pool)和一个全连接层构成。5个卷积部分构建残差连接，conv2_x～conv5_x的残差连接输入与输出维度不匹配，需采用1×1卷积核对输入特征图进行升维。为了提升模型的训练速度，有效缓解梯度弥散、消失等问题，各个卷积层进行非线性激活操作之前，先进行批量标准化操作，即增加一个BN(Batch Normalization)层[27]。

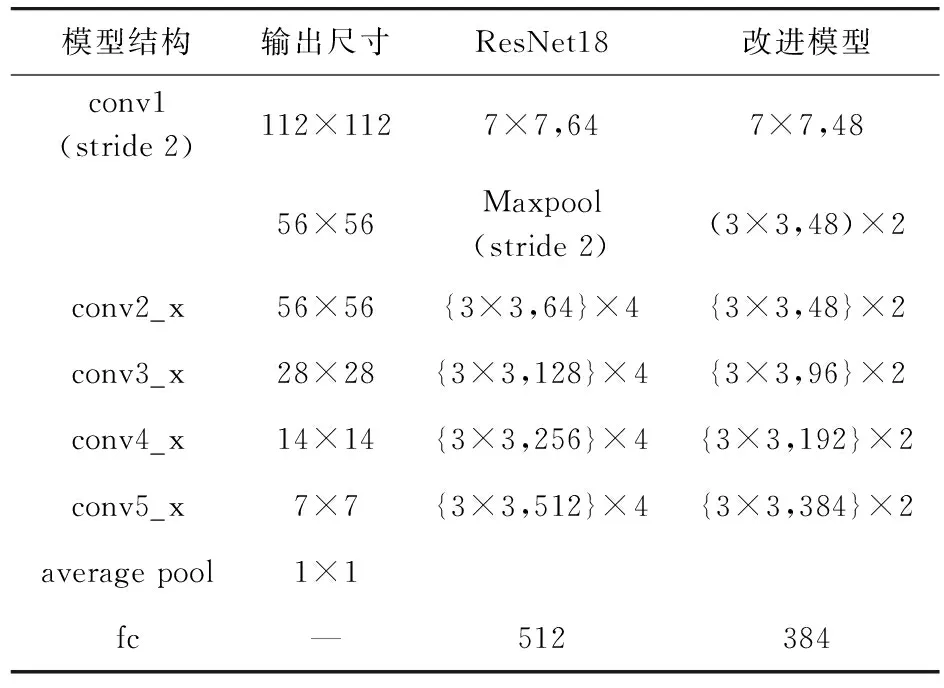
表1 改进残差网络模型与ResNet18结构对比Tab.1 Comparison between improved residual network model and ResNet18 structure

与文献[25]所设计的残差网络模型ResNet18相比，本文改进后的残差网络模型有以下几点创新：① 精简网络模型深度。ResNet18模型conv2_x～conv5_x卷积部分共有16个卷积层，精简后的模型conv2_x～conv5_x卷积部分仅有8个卷积层。② 压缩特征图维度。ResNet18模型conv1～conv5_x卷积部分输出特征图维度分别为64，64，128，256，512。改进后的模型conv1～conv5_x卷积部分输出特征图维度分别为48，48，96，192，384，是原来维度大小的75%，相应地，输入softmax分类器的特征维度也得到同等程度的降低。③ 利用2个3×3卷积层代替ResNet18模型的最大池化层。2个3×3卷积层均不进行激活和批量归一化操作，具备一定的滤波作用，减少网格效应[24]。

改进后的模型通过优化设计残差网络模型的结构，使其拥有更为强大的特征提取性能。同时，结合雷达时频图像特点，精简网络模型深度和输出特征图维度，在一定程度上可以缓解“过拟合”问题和用于分类的特征维度过高导致的“维度灾难”问题[7]。

对比分析来看，改进后的残差网络模型深度低于ResNet18模型，可能导致识别性能有轻微下降，但是，改进后的网络通过优化输出特征图维度和减少网格效应的操作，会进一步提升模型性能。综合分析，改进后的残差网络模型性能应该接近ResNet18模型。但是，改进后的残差网络模型在参数量和网络复杂度等方面远低于ResNet18模型，相应的时效性也远胜于ResNet18模型[23]。查看Matlab软件生成的2种模型规模，ResNet18模型规模大小约为40.2 Mb，本文改进后的残差网络模型规模大小约为10.1 Mb，约为ResNet18模型规模的25.1%。

3 仿真实验与分析

为了验证本文改进残差网络模型的性能，从识别率验证、识别鲁棒性验证2个方面设计仿真实验并进行分析。实验均在Matlab2020b平台上完成，仿真环境搭载Intel Core i7 2.8 GHZ处理器，操作系统为Windows10专业版64位。

3.1 雷达信号仿真参数设置

仿真第2节所述的7种常见的雷达辐射源信号，信号载频为40 MHz。其中，BPSK和BFSK均采用13位的巴克码，QPSK和QFSK编码序列长度为6，LFM调频斜率为20 MHz/μs，NLFM调频指数为500，BFSK的2个频率分别为35，40 MHz，QFSK的4个频率分别为35，40，50，60 MHz。在-15～0 dB信噪比(步长为1 dB)条件下随机生成训练样本，每个信噪比对应100×7个样本，共计11 200个训练样本。随机选取70%的训练样本作为网络训练的训练集，30%的训练样本作为网络训练的验证集。在同样的信噪比条件下随机生成测试样本，每个信噪比对应50×7个样本，共计5 600个测试样本。所有样本利用Matlab中的批量调整图像数据的augmentedImageDatastore函数，将样本尺寸调整成与各网络模型输入尺寸相匹配。

3.2 不同网络模型识别率对比

CNN对雷达信号时频图像的识别流程如下：首先，将图像数据集分成训练集、验证集和测试集；其次，利用训练集和验证集完成网络模型的学习训练；最后，利用训练好的模型对测试集中的样本进行识别率测试实验。

为了验证本文提出的改进残差网络模型性能，本次实验设计实验组和对照组。利用文中改进残差网络模型进行雷达辐射源信号识别为实验组。文献[25]提出了ResNet18模型，利用该模型进行雷达辐射源识别，以此为对照组1；文献[15]提出了GoogLeNet模型，以此为对照组2；文献[22]提出了MobileNetV2模型，以此为对照组3；文献[18]提出了的利用AlexNet模型进行雷达辐射源识别，以此为对照组4。训练参数均设置如下：初始学习率为0.001，最大训练轮数为8，学习率减小因子为0.5，减小学习率的周期间隔为1，其他训练参数设置均为默认值。

利用各训练好的模型对测试集进行分类识别，在-15～0 dB信噪比条件下的综合识别率对比如表2所示。本文改进残差网络模型识别率为95.9%，与ResNet18识别率接近，比MobileNetV2高约1.4%，比AlexNet高约3.1%，比GoogLeNet高约5.6%。这说明具有残差结构的网络模型性能优越，以残差网络为主体结构设计网络模型具有科学性，因此，本文提出的改进残差网络模型对7种雷达信号具有较高的识别率。

表2 各类网络模型综合识别率对比Tab.2 Comparison of comprehensive recognition rates of various network models

3.3 不同网络模型鲁棒性对比

鲁棒性验证包括2种实验：一种是低信噪比条件下的识别率对比；另一种是低信噪比条件下不同信号的识别率对比。

各模型在不同信噪比条件下的识别率对比如图4所示。随着信噪比的提高，各网络模型对雷达辐射源信号的识别率不断提高，当信噪比大于-5 dB时，各网络模型的识别率均为100%。对比来看，在任意信噪比条件下，改进残差模型对7类信号的识别率接近ResNet18模型，均高于其他3种模型，而且信噪比相对越低，识别率高的幅度相对越大。这说明改进后的残差网络模型在低信噪比条件下对7种雷达信号的依然具有较高的识别率。

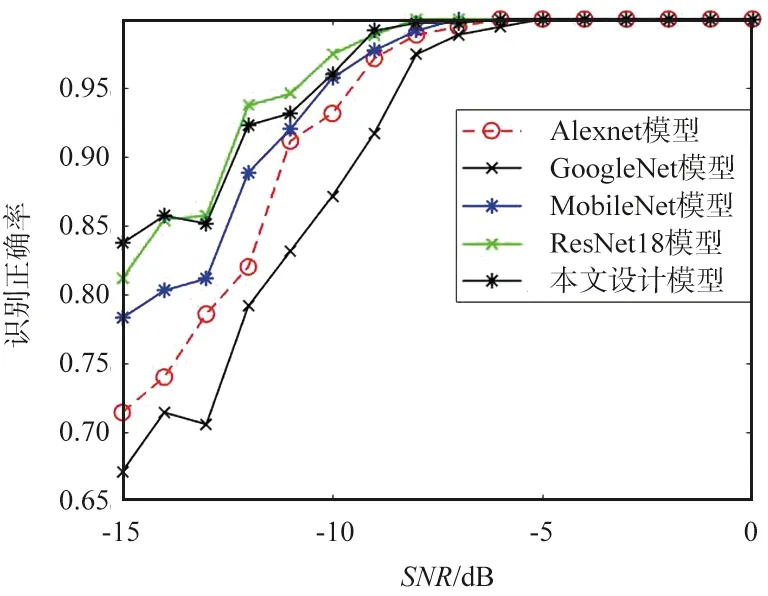
图4 各模型识别率对比Fig.4 Comparison of recognition rate of each model

在-15～-10 dB信噪比条件下，利用各模型对测试集信号进行分类识别，预测信号类别与真实信号类别生成的混淆矩阵如图5所示。BPSK，CW，LFM信号特征差异明显，所有模型各信噪比条件下均能对其进行准确识别，其余4种雷达辐射源信号，不同的网络模型有不同程度的混淆。对比来看，改进残差网络模型对ResNet18模型对NLFM信号的识别率低于其他4种模型，对BFSK，QFSK，QPSK信号的识别率均高于其他4种网络模型，而且改进残差网络模型对各类辐射源信号的识别较为稳定，对NLFM信号识别率最低，为66.3%，略逊于ResNet18模型，该模型对BFSK信号的识别率最低，为73.7%，远高于其他3种模型，AlexNet模型对QPSK信号的识别率不到50%；GoogLeNet模型对NLFM信号的识别率不到50%，对QPSK信号的识别率仅为55%；MobileNetV2模型对BFSK信号的识别率仅为50.67%。这说明改进后的残差网络模型在低信噪比条件下对“不易识别”的雷达信号依然具有较高且稳定的识别率。

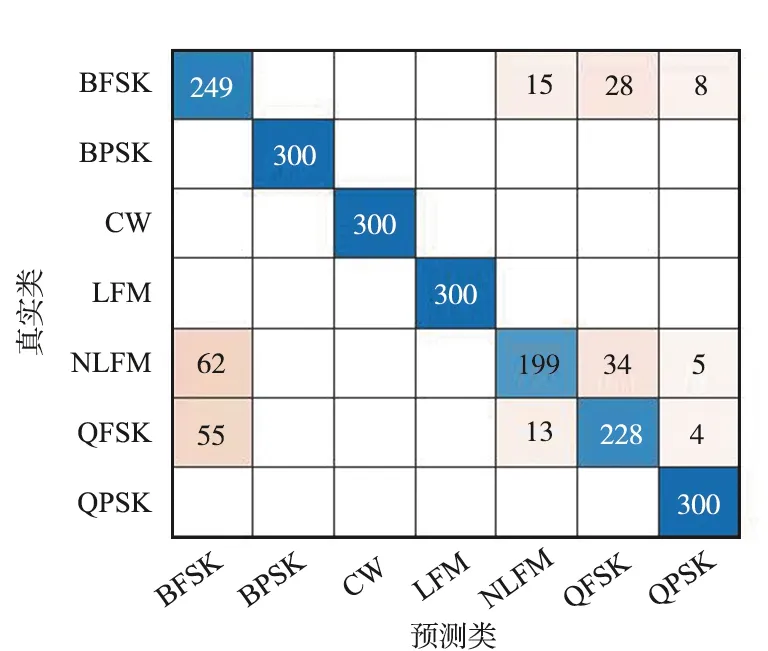
(a) 改进残差网络模型

(b) ResNet18模型

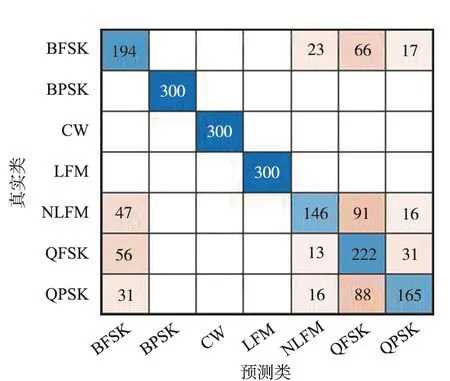
(c) GoogLeNet混淆矩阵

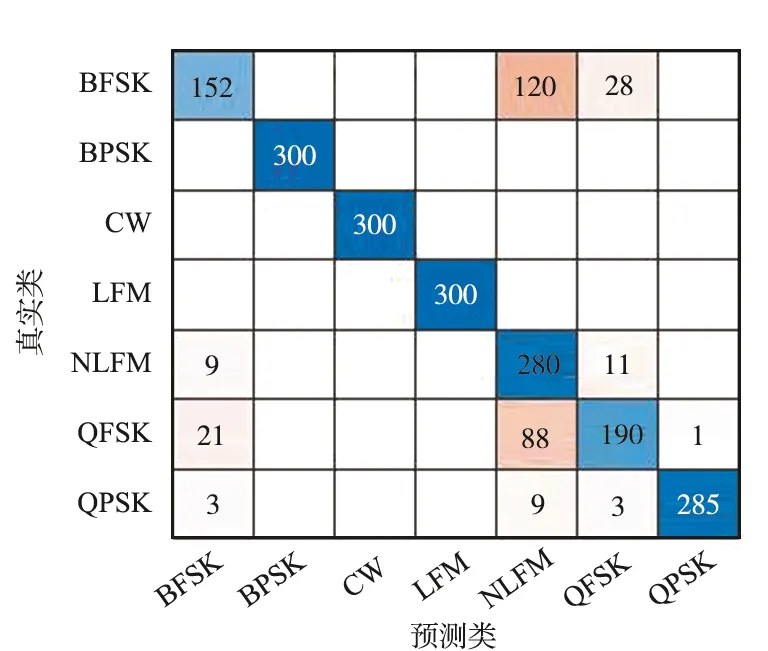
(d) MobileNetV2混淆矩阵

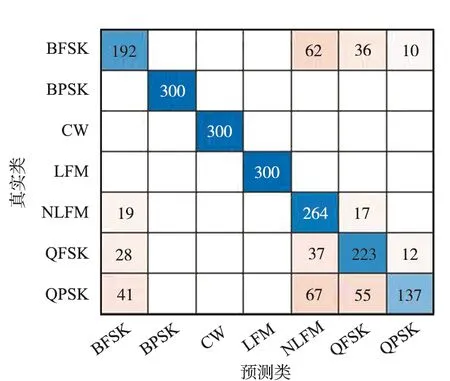
(e) AlexNet混淆矩阵图5 各网络模型混淆矩阵Fig.5 Confusion matrix of each network model

综合以上实验结果，可以验证本文提出的改进残差网络模型的有效性。改进残差网络模型具有残差网络的结构优势，能够缓解梯度消失的现象，保证有效信息传输。因此，识别率和鲁棒性均优于其他3种非残差网络模型。与残差网络ResNet18模型相比，在不同信噪比条件下的识别率和鲁棒性方面互有优劣，综合性能较为接近。但是，本文改进模型通过对模型体量和结构进行精简优化，兼顾了模型性能和复杂度。因此，改进后模型复杂度和模型规模大大减少，相应的时效性也得到提高，便于工程上的设计和应用。

4 结束语

本文提出了一种基于改进残差网络的雷达辐射源识别方法，改进后的残差网络模型以残差网络为主体结构，同时借鉴了轻量化与“去网格效应”的设计思想，在保证模型性能的同时，降低了模型的复杂度。实验结果证明，在综合考虑识别率、鲁棒性以及复杂度的情况下，本文改进后的模型性能优于其他文献提出的网络模型。同时，本文提出的模型以及设计方法可以为工程上的网络模型设计和应用提供参考。