NOMA增强的K层3D蜂窝网络建模与性能分析
赵家进,程 方,孙晶晶,邓炳光
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
0 引言
随着移动流量需求的不断增长和城市化进程的不断加快,蜂窝网络也从最初的发送功率大、密度小的宏基站逐步发展为发送功率小、密度大的微基站(Base Station,BS)、皮BS和家庭BS等[1-3]。因此对目前的蜂窝网络进行准确建模并准确分析网络性能至关重要。
采用随机几何理论进行蜂窝网络建模是目前的研究热点之一,通过随机几何理论中的点过程来模拟蜂窝网络中设备的分布,得到蜂窝网络的性能。目前大部分研究采用二维泊松点过程(Poisson Point Process,PPP)来建模蜂窝网络中BS和用户的分布[4-5]。但是仅仅适用于农村或者郊区场景,而不适用于城市高层场景中BS不仅在平面上随机分布,而且在高度上也随机分布的特性。因此,随机几何理论中的三维PPP则更符合城市高层场景中BS的分布情况[6-7]。
近年来,有部分研究进行了基于随机几何的三维蜂窝网络建模的研究。文献[7]考虑城市高层场景中单层三维蜂窝网络模型,将基站建模为三维PPP,推导了该网络的信干噪比(Signal to Interference plus Noise Ratio,SINR)覆盖率和特殊情况下的简洁表达式,分析了发送功率和有无噪声的影响。同时与实际情况中的实测数据进行了对比,证明采用三维PPP是更符合实际情况中BS的分布。文献[8]考虑密集城市环境下的最大瞬时SINR用户关联方案,分别推导了一般情况和干扰受限情况下的SINR覆盖率和平均用户速率,分析了网络中的发送功率、BS密度和路径损耗指数等的影响。文献[9]提出一种毫米波三维异构蜂窝网络模型,采用三维Matern硬核过程来建模网络中BS的分布,推导了该网络SINR覆盖率的表达式,为融合毫米波的下一代蜂窝网络提供了一个有效的模型。文献[6]提出三维密集小区无线网络,考虑视距和非视距条件下不同的信道模型,同时研究了真实传播的整体效应,获得了该网络的下行覆盖率。文献[10]提出了异构蜂窝网络的通用3-D模型,同时提出了一种新的传输方案来缓解干扰问题,并推导了一般的K层网络相应的覆盖率表达式,确定了新方案在增强网络干扰管理方面的优势。
作为一种新型的多址技术,非正交多址(Non-orthogonal Multiple Access,NOMA)可以在5G场景中发挥重要的作用。NOMA关键思想是在同一频段上对不同用户分配不同的功率,实现了在同一频段中以不同的服务质量服务多个用户。因此,NOMA技术可以提高蜂窝网络的频谱效率和改善蜂窝网络中用户的接入[11-12];同时,由于其独特的编码方式,NOMA可以降低设备功耗和网络传输时延,提高网络传输的可靠性。这使得NOMA在环境监测、智慧城市、车联网和工业控制等应用场景发挥重要的作用[13]。
NOMA与蜂窝网络融合,将NOMA技术加入目前的蜂窝网络建模与性能分析中是一种可行的方案。文献[14]首次采用随机几何理论将NOMA技术应用于蜂窝网络的分析,考虑了一种多输入多输出(Multiple Input Multiple Output,MIMO)-NOMA结合的多层蜂窝网络,宏BS采用MIMO技术服务多用户,其他BS层采用NOMA技术,其都服从独立的二维PPP,推导了SINR覆盖率和频谱效率的一般表达式,并分析了发送功率和功率分配因子等的影响,同时对比了正交多址(Orthogonal Multiple Access,OMA)的网络,证明所提网络具有优越的性能。文献[15-16]研究了NOMA增强无人机的网络,得到网络的中断概率和平均遍历速率的一般表达式。但目前还没有研究将NOMA技术融入到城市高层场景的蜂窝网络建模与性能分析中。因此,需要利用结合NOMA技术采用随机几何理论对城市高层场景的蜂窝网络进行建模与分析。
1 NOMA中K层3D模型
1.1 网络分布
城市高层场景示意如图1所示,考虑了城市高层场景中BS的分布,其在平面和垂直方向上都随机分布。本文建立了一种下行NOMA增强的K层3D蜂窝网络,每一层BS的分布服从三维PPP过程Φk,k=1,2,…,K,密度为λk,发送功率为Pk,该三维蜂窝网络模型中BS位置分布如图2所示。图中给出了3种类型的BS分布,从微BS到家庭BS,发送功率逐渐减小,但密度逐渐增加。每层BS采用NOMA技术以服务多个用户,如图3所示。假设仅考虑2种用户的情况,每个用户设备都配备一根天线并且都会与距离最近的BS通信。根据Slivnyak’s定理,主要对位于三维空间中原点处的典型用户进行分析。
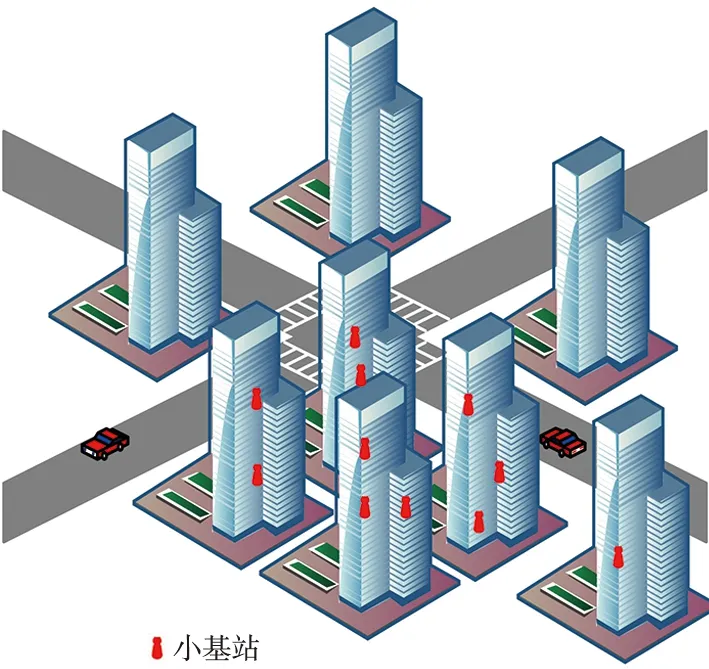
图1 城市高层场景示意Fig.1 Schematic diagram of urban high-rise scenes

图2 BS位置示意Fig.2 Schematic diagram of BS location

图3 网络模型Fig.3 Network model
与OMA中用户关联不同,NOMA通过给用户分配不同的功率来利用功率稀疏性进行多址接入。因此,对于典型用户,其接收到来自第i层第j个BS的平均接收功率为:
(1)
式中,Pi为第i层基站的发送功率;hi为小尺度衰落参数,假设每一层基站与用户之间经历平均值为1的瑞利衰落,可以表示为hi~exp(1);η为频率相关系数;αi为路径损耗指数;ri,j为典型用户与第i层第j个基站之间三维空间距离。
1.2 网络分布
在不损失通用性的情况下,考虑每个BS在前一轮用户关联过程中与一个用户关联,称为固定用户。为简单起见,假设关联用户和连接的第k层BS之间的距离是相同的,可以是任意值,表示为rk,而典型用户与每个BS的距离为随机值。与小尺度衰落相比,路径损耗为主要部分,因此在近用户侧应用串行干扰消除(Successive Interference Cancelation,SIC)操作。然而,并不预先确定典型用户是近用户(用户m)还是远用户(用户n),在分析用户的SINR时,需要有以下近用户情形和远用户情形。
① 近用户情形。当典型用户为近用户时,即典型用户到BS的距离小于关联用户到BS的距离(r (2) 如果成功解码固定用户的信息,固定用户的干扰就可以被消除,典型用户就可以解码自己的信息,对应的SINR表达式为: (3) 对于由相同BS服务的固定用户(即远用户),通过NOMA技术可以直接解码自己的信息,而典型用户的信息则作为干扰,因此,固定用户的SINR可以表示为: (4) ② 远用户情形。当典型用户为远用户时,即典型用户到BS的距离大于关联用户到BS的距离(r>rk),对应图2中用户n,对于固定用户将先解码典型用户的信息,对应的SINR可以表示为: (5) 如果成功解码典型用户的信息,典型用户的干扰就可以被消除,固定用户就可以解码自己的信息,对应的SINR表达式为: (6) 对于由相同BS服务的典型用户(即远用户),通过NOMA技术可以直接解码自己的信息,而固定用户的信息则作为干扰。因此,典型用户的SINR可以表示为: (7) 由于第k层BS和典型用户之间的距离是随机的,需要通过三维PPP的性质来推导。三维PPP中用户与BS之间距离为: (8) 因此,典型用户与距离最近的第k层BS之间距离的概率密度函数(Probability Density Function,PDF)为: (9) 典型用户与第k层BS关联的概率为: Ak= (10) 式中, 参考文献[8],可以得到: (11) 即典型用户与关联的第k层BS之间距离的概率分布函数为Frk,0(x)=1-[rk,0>x]。因此,典型用户与关联的第k层BS之间距离的PDF为: (12) 在得到用户接收到BS的总干扰后,需要对干扰进行拉普拉斯变换,是求SINR覆盖率的重要一步,干扰的拉普拉斯变换通过以下推导得到: LIr(s)=[exp(-sI)]= (13) 式中,步骤(a)由三维PPP的概率生成函数(Probability Generating Functional,PGFL)得到,函数形式为步骤(b)根据指数分布的矩母函数得到。 SINR覆盖率可以定义为一个典型用户在一定的SINR阈值下成功传输信号的概率,可以表示为: PC=(SINR>T)。 (14) 根据NOMA解码策略,考虑到典型用户为近用户和远用户这2种情形,分开对这2种情形的典型用户进行SINR覆盖率分析。 ① 近用户情形(r=rk)。典型用户成功解码自己信息的步骤为:典型用户先解码由相同BS服务的固定用户的信息,经过SIC过程,典型用户解码自己的信息。 因此,在近用户情形下,典型用户关联第k层BS,其SINR覆盖率可以表示为: PCk,near(r)=(SINRk,t→f,near>Tf,SINRk,t,near>Tt), (15) 式中,Tf,Tt分别表示固定用户和典型用户的SINR阈值。 典型用户为近用户,满足am,k-an,kTf≥0条件时,SINR覆盖率可以表示为: PCk,near(r)= (16) PCk,far(r)= (17) 因此,当典型用户与第k层BS关联时,典型用户的SINR覆盖率可以表示为: (18) 式中,Ak为典型用户关联第k层BS的概率。 得到SINR覆盖的表达式后,可以通过SINR覆盖率的表达式推导得到网络的频谱效率和ASE。 参考文献[17],频谱效率可以表示为 (19) 式中,PC(ω)为SINR覆盖率。 在所提网络模型中,典型用户关联第k层BS时,考虑到典型用户为近用户和远用户这2种情形,分成这2种情形来计算典型用户关联BS时的频谱效率。 ① 典型用户为近用户时,频谱效率可以表示为: (20) 式中, PCk,f,near(ω)=(SINRk,f,near>ω)= (21) PCk,t,near(ω)=(SINRk,t,near>ω)= (22) ② 典型用户为远用户时,频谱效率可以表示为: (23) 式中, PCk,f,far(ω)=(SINRk,f,far>ω)= (24) PCk,t,far(ω)=(SINRk,t,far>ω)= (25) 结合式(20)和式(23),第k层的可实现的频谱效率为 Rk=Rk,near+Rk,far。 (26) 在得到频谱效率的表达式后,ASE也就可以得到: ASEk=λkRk, (27) 式中,λk为第k层BS的密度;Rk为第k层的频谱效率。 采用蒙特卡罗仿真和数值结果来分析该NOMA增强的K层3D蜂窝网络。考虑该蜂窝网络包含3种类型的BS(微BS、皮BS和家庭BS),分析了网络中的相关参数如BS密度、功率分配因子对网络的相关性能的影响。除非另有说明,参数值如表1所示。 表1 网络仿真参数Tab.1 Network parameters for simulation 图4展示了在Tf=Tt=T时不同类型BS的SINR覆盖率与阈值的关系。从图中可以看出,覆盖率会随着阈值增加而减小,而阈值为1 dB时,3种类型BS的覆盖率都为0,主要是由于不满足am-anT≥0,使得阈值降为0。同时,微BS和皮BS的覆盖率曲线拟合,而家庭BS的覆盖率比前2种基站小一些,但整体上,该网络的3种类型BS提供差不多的覆盖。 图4 不同类型BS的覆盖率与阈值的关系Fig.4 Coverage probability as a function of the threshold for different types of BS 图5展示了不同功率分配因子下SINR覆盖率与典型用户的SINR阈值和固定用户的SINR阈值的关系的三维曲面图。从图中可以看出,覆盖率会随着2个阈值的增加而减小,而到达一定的阈值后覆盖率为0,这主要是由于到一定的阈值,就不满足am-anf≥0或am-anTt≥0这2个条件。同时可以看出,SINR覆盖率主要是随着典型用户的阈值Tt变化,而固定用户的阈值Tf则影响较小。 图5 不同功率分配因子下皮BS覆盖率与2个阈值的关系Fig.5 Coverage probability of pico BS as a function of two thresholds for different power allocation factors 图6展示了在Tf=Tt=T时不同功率分配因子下SINR覆盖率与SINR阈值的关系。随着对远用户的功率分配因子增加,覆盖率会逐渐增加,达到覆盖率为0的阈值越大,主要是由于需要满足am-anT≥0的条件,当am增加,an减小,从而使得达到覆盖率为0的阈值T增加。同时对比了采用OMA增强的三维蜂窝网络模型(典型用户没有近用户与远用户之分,也没有固定用户,即an→1)。可以看出采用OMA增强的模型比所提模型在覆盖率上有微弱优势。蒙特卡罗仿真结果和理论结果的拟合表明采用随机几何理论分析过程的正确性。 图6 不同功率分配因子下皮BS覆盖率与阈值的关系Fig.6 Coverage probability of pico BS as a function of the threshold for different power allocation factors 图7展示了网络的频谱效率与皮基站密度的关系。从图中可以看出,随着皮BS密度的增加,3种类型BS的频谱效率都逐渐减小,主要是由于皮BS密度增加,皮BS的个数增加,用户与最近的皮BS的距离减小,用户会更偏向于与皮BS相关联,使得另外2种类型BS的频谱效率减小,皮BS数量的增加也会使得皮基站的频谱效率减小。 图7 不同类型BS的频谱效率与皮BS密度的关系Fig.7 Spectral efficiency as a function of the densities of pico BS for different types of BS 图8展示了不同功率分配因子下皮BS频谱效率与密度的关系。随着皮BS密度的增加,其频谱效率减小,而OMA增强的皮BS频谱效率没有什么变化,而对远用户的功率分配因子增加,则会使得皮BS的频谱效率减小,在远用户的功率分配因子较大时,SINR覆盖率会较大,但频谱效率会较小。因此,需要考虑功率分配因子对SINR覆盖率和频谱效率的影响。同时,与采用OMA增强的皮BS相比,采用NOMA增强的皮BS可以大幅提升网络的频谱效率,这使得OMA增强的皮BS对SINR覆盖率上的微弱优势可以忽略不计。 图8 不同功率分配因子下皮BS频谱效率与皮BS密度的关系Fig.8 Spectral efficiency of pico BS as a function of the densities of pico BS for different power allocation factors 图9展示了网络的ASE与皮BS密度的关系,可以看出,随着皮BS密度的增加,皮BS的ASE会增加,而微BS和家庭BS的ASE减小,主要是由于皮BS频谱效率的降幅比皮BS密度的增小,使得皮BS的ASE随着皮BS密度的增加而增加,而微BS和家庭BS的ASE是频谱效率乘上相应BS的密度,所以和频谱效率趋势一样。 图9 不同类型BS的频谱效率与皮BS密度的关系Fig.9 ASE as a function of the densities of pico BS for different types of BS 图10展示了不同功率分配因子下皮BS频谱效率与其密度的关系。可以看出,皮BS的ASE随着远用户的功率分配因子增加而减小。同时可以看出采用NOMA增强的模型比OMA增强的模型在ASE上的优越性。 图10 不同功率分配因子下皮BS频谱效率与皮BS密度的关系Fig.10 ASE of pico BS as a function of the densities of pico BS for different power allocation factors 本文提出一种NOMA增强K层3D蜂窝网络模型,其中K层BS采用三维PPP进行建模。利用随机几何学中的理论,推导得到K层BS的SINR覆盖率、频谱效率和ASE的一般表达式。蒙特卡罗仿真与理论推导结果拟合,证明理论分析过程的正确性,同时分析皮BS密度,功率分配因子对网络的影响,对比OMA增强模型,所提NOMA增强的城市高层场景蜂窝网络模型的优越性。该模型可以在未来城市高层场景中BS的设计和部署提供一个理论上的参考。下一步的研究将放宽BS在同一频段只服务2个用户的假设,使得可以同时服务多个用户。
1.3 距离分布

2 关键性能指标
2.1 干扰的拉普拉斯变换

2.2 SINR覆盖率

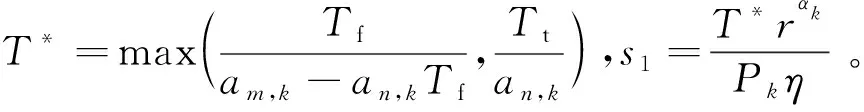
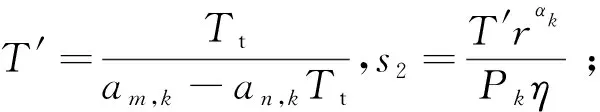

2.3 频谱效率及ASE

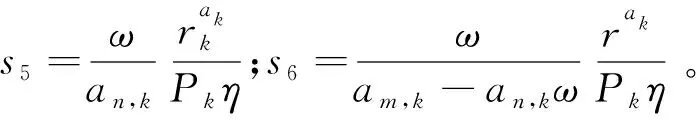
3 仿真与数值结果分析








4 结束语

