GaAs多线切割切片翘曲度的有限元分析

康洪亮

(中国电子科技集团公司第四十六研究所，天津 300220)

翘曲度（Warp）是描述晶片加工质量的一个重要几何参数。翘曲度定义为切片的中心平面与基准参考平面之间的最大距离与最小距离之差。翘曲度属于体缺陷，除在晶体生长中调整热场和拉晶参数外，切片线切工艺中钢线张紧力、钢线速度、进给速度、钢线线径、温度等都会影响翘曲度，研究线切工艺参数与切片翘曲度间关系，对于控制切片翘曲度具有重要意义。科研生产中当切片翘曲度指标超标时，需对影响翘曲度的工艺参数进行全面的分析研究，开展工艺试验，耗资费时。因此极有必要研究两者之间的理论关系，为优化相应工艺参数，达到快速改善切片翘曲度的目的。采用Abaqus软件对砷化镓晶棒线切过程进行有限元建模分析，在有限元模型中，晶片总厚度偏差为零，即可将未变形前切片面视为基准面，切片面受热变形后的平面视为中心平面。采用切片表面节点变形位移来间接反映切片翘曲度。

1 多线切割热分析理论基础

研究多线切割过程中的热力学问题主要包括两方面内容：传热问题分析，确定模型的线切温度场；热应力问题，确定模型的应力应变场。结合镀铜钢线锯切割砷化镓晶棒时，温度场直接影响切片热应力应变场，而热应力场对温度场耦合影响几乎可忽略，因此本文对砷化镓晶棒线切热分析选用Abaqus顺序耦合热应力分析法。

1 多线切割温度场分析基础理论

线切过程中砷化镓晶棒的温度随热载荷移动重新分布，线切温度场与热载荷加载时间有关，因此属于非稳态传热。

1.1 温度场数学模型

线切过程中，热源位置是变化的，根据傅立叶传热定律与能量守恒定律，建立砷化镓晶棒线切过程中无内热源三维传热瞬态温度场的微分方程：

式(1)中，kx、ky、kz分别为砷化镓晶体沿x、y、z方向的热传导系数；cT、ρ分别为晶体的比热容、密度；T为晶体温度。

式(1)左端表示由x、y、z方向传入晶体的热量，右端表示晶体升温所需热量。

在求解域（Ω）的温度场分布应满足的边界条件。边界条件分如下三类：

第一类边界条件Γ1(给定温度值)，是强制边界条件：

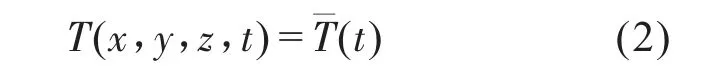
第二类边界条件Γ2(给定热流密度)：

式(3)中，qv为切口表面上的热流密度，nx、ny、nz为边界外法线的方向余弦。

热流密度为物体单位面积横截面在单位时间内通过的热量。对于线切加工的热流密度大致可以理解为施加在单位面积上的功率[1-4]：

式(4)中，P为线锯切割功率，ξ表示线锯切割能量损耗系数，为无量纲量，A为切口横截面积。线锯切割功率P可表示为钢丝张紧力与钢丝运动速度的乘积：

根据线锯切割加工原理得到线切能量损耗系数ξ可以近似表示为：

式(6)中，α为钢丝的弓角。

每一分析步材料切除层体积V可以近似表示为[1]：

式(7)中，L为钢丝与工件接触长度；d为切口宽度；h为每一分析步晶体进给长度。

因此，把式(5)和式(7)代入式(4)便可得到线切加工中的热流密度[1-3]：

式(8)中，vw为晶体进给速度；tinc为每一分析步时间。

第三类边界条件Γ3(给定对流换热系数)：

式(9)中，h为对流换热系数，自然对流换热系数与强制对流换热系数其值有所不同。

1.2 热应力分析基础理论

砷化镓晶体为脆性材料，本文不考虑其塑性，根据热弹性力学理论。当物体内部温度的分布不均会引起部件热胀冷缩，在部件内部产生热应力，依据线性热力学理论，物体内部微元体的总应变由温度变化引起的应变和应力引起应变两部分组成。则由温差ΔT引起的应变为εfij=[α]ΔT，总应变εij为：

式(10)指标形式为：

除了物理方程与普通的弹性问题有所不同，热应力问题的平衡方程、边界条件以及几何方程均相同，根据虚功原理δU-δW=0得：

将结构离散化求变分，最后得到单元节点力与节点位移关系式：

式(14)中：pfe为温度等效载荷。由于温度场直接影响切片热应变场，而热应变场对温度场的耦合影响几乎可忽略不计，因此本文选择顺序耦合热应力应变有限元分析模型。

2 砷化镓晶棒多线切割热分析有限元模型建立

首先建立砷化镓晶体线切温度场三维有限元模型，采用生死单元算法来模拟材料去除，通过施加动态载荷步来模拟热载荷的移动，在切口表面和新形成线切晶面设置为强迫对流换热边界，在晶体外表面设置为自然对流换热边界，如图1所示。

图1 砷化镓晶棒多线切割Abaqus有限元建模示意图

图1为砷化镓晶棒多线切割Abaqus有限元建模示意图。其中分析步类型设置为General：Heat transfer(Transient)，在Interaction功能模块中设置对流换热边界，在“预定义场”中设置初始温度边界条件为室温22℃，模型选用DC3D8(八节点隐式线性热传导单元)。

然后进行热应力分析，将温度场结果作为边界条件，删除之前定义的分析步和“预定义场”。分析步类型设置为General:Static，General，“预定义场”，在Load模块中Create Predefined Field，选定类别Other中Temperature，在Distribution里选择From results or database file：File name：导入文件名，文件为之前温度场结果文件，单元类型选择C3D8L（八节点六面体线性非协调模式单元）。

本文在计算热载荷qv时，室温设为22℃，钢丝速度为5 m/s、晶棒进给速度为0.15 mm/min，钢丝张紧力为20 N、钢丝弓角为1.5°。晶体表面与空气的自然对流换热系数一般为1～10 W/(m2·℃)，与冷却液的强迫对流换热系数为1×l04～3×l04W/(m2·℃)。但随着切割深度的不断增加，冷却液进入切缝的能力也在逐渐变化，参考文献[1]并结合实验，切缝中的对流换热系数可归纳为：

式(15)中，z为切割深度坐标，原点在晶棒圆心。

砷化镓晶棒材料属性见表1。

表1 砷化镓晶棒材料属性

3 热分析仿真结果分析与讨论

3.1 钢丝张紧力对翘曲度影响

在钢丝速度vc=5 m/s，晶棒进给速度vw=0.15 mm/min，钢丝线径d=0.12 mm时，通过改变式(8)中张紧力F1，分析钢丝张紧力与切片翘曲度之间关系，如图2所示。

图2 钢丝张紧力对砷化镓切片翘曲度的影响

从图2中可以看出，随着张紧力的增大，翘曲度逐渐减小。这是因为张紧力越大，钢丝绷得越紧，钢丝的弓角越小，切削能量损耗系数越小，进入切片内部热量减小，而切片散热能力大小基本相似，因此切片温升有所减小，切片翘曲度减小。然而钢丝张紧力过大时，钢丝易达到抗拉强度导致拉断，同时会降低导轮和过线轮的使用寿命，因此应该综合考虑选择基本满足晶片几何参数条件下的张紧力。

3.2 钢丝速度对翘曲度影响

在钢丝张紧力F1=20 N，进给速度vw=0.12～0.22 mm/min，钢丝线径d=0.12 mm时，通过改变式(8)中钢丝速度vc，分析钢丝速度与切片翘曲度之间关系，如图3所示。

图3 钢丝速度对砷化镓切片翘曲度的影响

图3为分别在不同的进给速度下钢丝速度对切片翘曲度影响。从图3中可以看出，同一进给速度下，随着钢丝速度增大切片翘曲度逐渐增大。这是因为钢丝速度越大，线锯切割功率越大，线切阻力越大，切削产生热量越多，而钢丝弓角保持不变，即切削热损耗系数不变，单位时间进入切片内热量增多，切片散热能力不变，切片翘曲度变大。

3.3 进给速度对翘曲度影响

在钢丝张紧力F1=20 N，钢丝速度vc=4.5～6.5 m/s，钢丝线径d=0.12 mm时，通过改变式(8)中晶棒进给速度vw，进一步分析进给速度对切片翘曲度的影响情况，结果如图4所示。可以看出同一钢丝速度下，随着进给速度增大，切片翘曲度逐渐增大。这是因为随着进给速度增大，单位时间内材料切除量增多，产生热量增多，同时切削热损耗系数也越大，单位时间进入切片内热量越多，而切片散热能力基本保持不变，切片翘曲度增大。比较图3与图4发现，相较于钢丝速度变化，进给速度变化对切片翘曲度影响更明显。

图4 进给速度对砷化镓切片翘曲度的影响

3.4 钢丝线径对翘曲度影响

在钢丝张紧力F1=20 N，钢丝速度vc=5 m/s，进给速度vw=0.15 mm/min时，通过改变钢丝线径d=0.12 mm，分析线径与翘曲度关系，如图5所示。

图5 不同线径对砷化镓切片翘曲度的影响

由于砷化镓晶棒价格昂贵，较小线径可提高单位尺寸砷化镓晶棒出片数，钢丝线径减小成为一种发展趋势。钢丝线径对切片翘曲度影响在计算模型中主要通过改变切缝宽度d体现。从图5可以看出：随着钢丝线径减小，切片翘曲度逐渐增大，这是因为随着钢丝线径减小，线切区域减小带来切缝变窄，单位面积作用热载荷增大，通过热传导进入切片热量增多，而切片散热能力减弱，升温越高，因此不同线径之间翘曲度相差明显。但线径过小，会导致线切过程中因偶发因素导致断线的几率升高，对于砷化镓晶棒而言，由于砷化镓材料硬度较小，断线后重新布线续切也会导致切片表面产生线痕。因此在实际生产中，需要综合考虑各方面因素，选择最优的线径。

4 结束语

本文建立了砷化镓晶棒多线切割顺序耦合热应变分析有限元模型，以切片表面节点位移反映切片翘曲度。首先建立温度场三维有限元模型，模拟切割过程温度场分布；然后以温度场结果为边界条件，建立热应变分析模型；按照不同的张紧力、进给速度、钢线速度等工艺参数组合进行仿真模拟，计算出相应的翘曲度值，研究翘曲度与各工艺参数之间的关系。结果表明：多线切工艺参数主要通过影响切片散热能力影响切片翘曲度。切片翘曲度随着钢丝速度和进给速度增大而增大，随着钢丝张紧力和线径增大而减小，且相对于钢丝速度进给速度变化对切片翘曲度影响更明显。在实际生产中选择工艺参数时，在设备允许的条件下应选择较大的钢线张紧力，在兼顾生产效率和成本的条件下，应选择较小的钢线速度、晶棒进给速度和钢线线径。