直写铸造蜡沉积成型数值模拟分析与实验

莫海军，王顺栋，梁道明

(华南理工大学机械与汽车工程学院,广东广州 510641)

0 前言

传统熔模铸造工艺中蜡模的制造通常借助金属模具完成，但是金属模具制作周期长、开模成本高，不适合单铸件或中小规模的生产，无法实现对零件研发的快速响应[1-2]。快速熔模铸造技术(Rapid Investment Casting, RIC)具有快速成型技术中成型时间短的优点，可将熔模铸造工艺的研发周期缩短至2周，降低95%的生产成本[3]。铸造蜡因其成型温度低、可重复利用、材料黏度随温度变化明显、同一温度下材料随着剪切速率增大而黏度降低[4]，符合快速成型技术材料的要求，引起了学者们的关注。OTTNAD等[5]提出了一个基于压电元件的定量供墨3D打印头并进行了蜡滴打印研究，验证了采用压电元件进行蜡滴打印的可行性。MA等[6]提出一种基于微流气动的挤出直写打印技术并进行了石蜡打印研究，验证了该方法的可行性。赵佳伟、彭子龙等[7-8]探究了蜡材料的其他成型方式，搭建了电场驱动的喷射打印平台，采用脉冲方式打印了80号微晶蜡滴。考虑对成型件的要求，本文作者采用热辅助直写技术打印铸造蜡材料。

铸造蜡热辅助直写(Direct Ink Writing，DIW)成型的过程中，经历挤出和沉积两个阶段，挤出段和沉积段具有相互耦合关系，两者共同作用于熔丝的成型。熔丝的几何特性、排列情况均会影响成型件层间间隙及冷却后熔丝间的黏结质量[9]。因此，精确控制熔融聚合物的挤出和沉积过程至关重要。现有研究中，挤出丝的几何结构通常被简化为具有圆形截面的广义圆柱体或具有长方形截面的广义长方体[10-12]。但是在实际打印过程中，熔丝的截面非理想几何形状，这会导致仿真结果存在误差，影响仿真精度[13]。另外，铸造蜡材料成型质量易受打印工艺参数的影响。因此，本文作者借助Fluent软件，对铸造蜡挤出沉积流场进行数值模拟分析。通过数值仿真与实际打印实验相结合的方式，分析挤出压力、喷头半径、喷头距基板距离及打印速度对熔丝打印及成型质量的影响，分析在不同打印参数下熔丝的形状，为DIW仿真中准确化简截面形状和实际铸造蜡DIW成型中的最优工艺参数选择提供参考。

1 铸造蜡DIW打印方案及挤出沉积理论模型

1.1 热辅助铸造蜡DIW打印方案

铸造蜡材料强度低，不易制作成卷材，与常见的DIW液态材料不同，常温下为固态。因此，需搭建一个热辅助DIW打印平台。在打印喷头处配备加热结构、隔热结构，实现对材料的加热和控温，将铸造蜡材料加热到熔融状态，便于打印。但这将导致打印喷头质量较大，为保证打印的精度，打印平台整体结构采用龙门式结构，采用双Z轴共同驱动打印喷头移动，如图1所示。打印过程：固态铸造蜡材料在加热腔中加热至熔融状态，受空压机提供的压力经过喷嘴从加热腔中均匀挤出，并按设定轨迹在挤出腔体和打印基板的相互移动配合下沉积在基板上，逐条逐层进行打印，最终打印成一个成型件。考虑到铸造蜡材料的硬度较低，熔丝太细会导致硬度不够，熔丝太粗精度降低，因此选用0.6、0.8 mm两种规格的喷嘴进行研究。

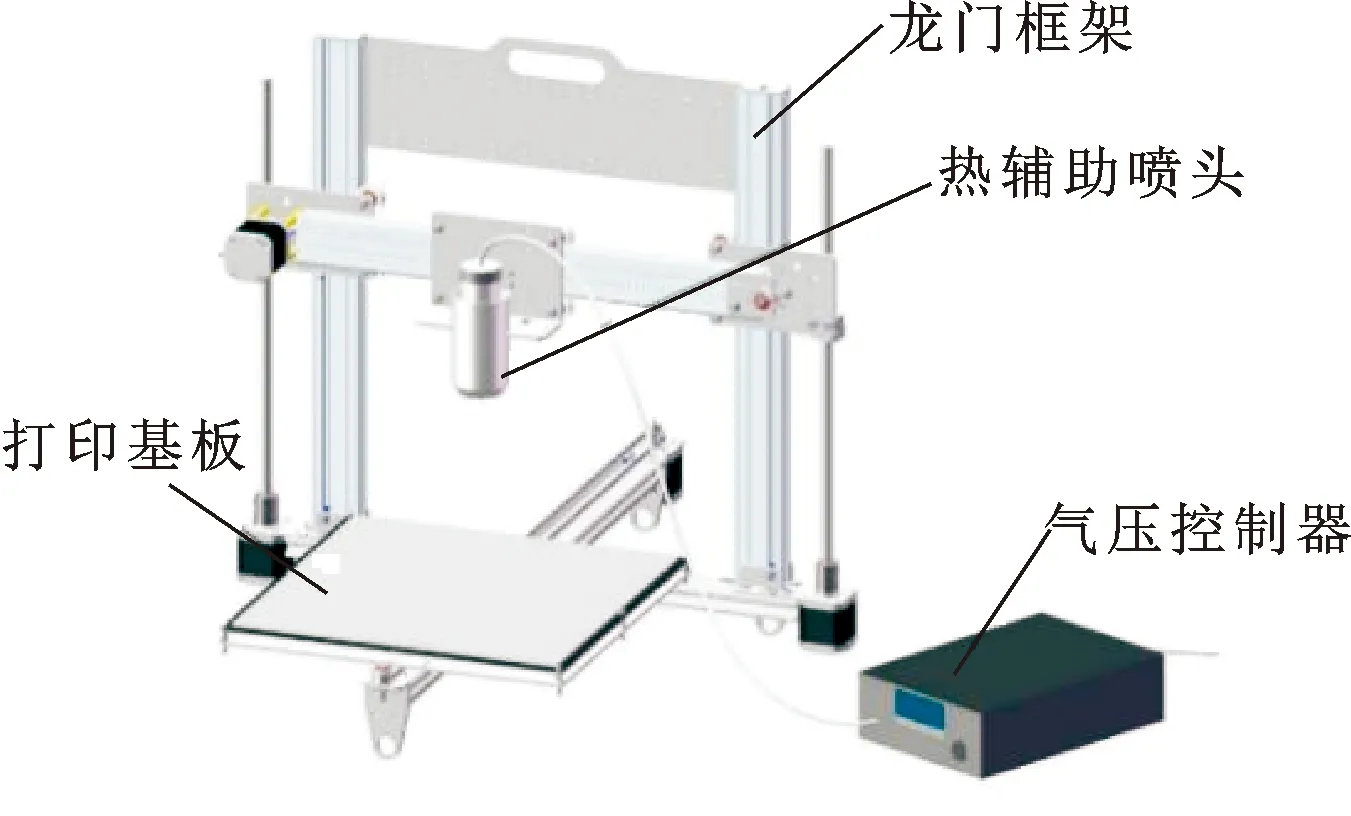
图1 铸造蜡热辅助DIW打印平台

1.2 挤出沉积流场理论模型的构建

熔融态铸造蜡材料DIW过程的实质是将黏性材料经外力挤出并沉积到相对移动的基板上，材料的形状在喷嘴和基板的共同作用下发生改变，材料形状的改变可以看作是流场的改变。熔丝形成的过程可以看作是黏度流体的自由表面流动，自由表面的变化是熔融状态铸造蜡流体和空气气液两相相互作用的结果。针对整个挤出沉积过程，作如下假设：

(1)材料是不可压缩的牛顿流体，密度为常数；

(2)整个挤出沉积过程时间短，忽略喷嘴与基板间小间隙的热量损失，所以整个挤出沉积过程看作是等温的，材料与空气之间无热交换，不考虑能量方程；

(3)忽略温度对黏度的影响；

(4)流体在喷嘴内部和基板上的流动可看作是与喷嘴内部和基板无相对滑动。

因此，文中涉及的挤出沉积过程可以看作为带有自由表面、黏性、不可压缩流体的恒温非稳态流动。基于Navier-Stokes方程和VOF方程建立理论模型。常黏度条件下不可压缩流体的Navier-Stokes方程为

(1)

不可压缩流体的连续性方程：

(2)

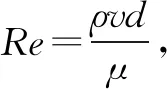
熔体的表面张力相对重力的作用程度通常用邦德数Bd来表征，当Bd较小时，液体在流动过程中，表面张力起主导作用。

(3)

式中：σ为表面张力系数，N/m；r为喷嘴的半径，m。

文中研究的铸造蜡材料表面张力系数σ为0.02 N/m，根据公式(3)可得材料在喷嘴处的Bd最大值为0.294 4，Bd小于1，因此材料在挤出过程中表面张力起主导作用，在计算过程中可以忽略重力。

因此，Navier-Stokes方程中的f化简为

(4)

此外，为获取两相界面的信息，得到打印材料的流动情况，采用流体体积(Volume of Fluids，VOF)法捕捉气液两相的交界面变化。

1.3 挤出喷头流场的数值分析

1.3.1 挤出喷头的几何结构及数值分析模型

挤出喷头的结构及尺寸如图2所示(以喷嘴0.6 mm为例)。其中，挤出腔体的内径为28 mm，喷嘴腔体的内径为1.6 mm，喷嘴口挤出腔体的内径为0.6 mm。流场分布可直接反映材料挤出的状态，文中借助Fluent软件对挤出腔体内的流场进行数值模拟，探究腔体内压力和挤出速度随轴线位置的变化。挤出腔体的上表面为流场入口，喷嘴挤出口腔体下表面为流场出口，入口和出口均设置为压力边界条件，进口压力(总压)设置为700 kPa，出口压力(静压)设置为0，腔体壁面为无滑移壁面条件。网格全部划分为结构化网格。

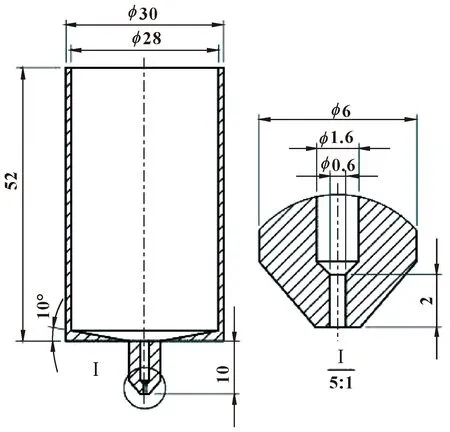
图2 挤出喷头剖面图

1.3.2 挤出喷头内流场分析

图3所示为稳态情况下挤出喷头内流场压力分布情况及挤出压力、材料挤出速度随中心轴轴向位置变化的情况。可以看出：在挤出腔体内部及喷嘴腔体内部流场的变化很小，在进入喷嘴口挤出腔体后流场发生了急剧的变化。由图3(b)(c)可以更直接地看出，挤出腔体内挤出速度非常慢，速度变化不明显，可以近似地看作等速运动；材料进入喷嘴腔体后，速度发生了轻微的变化，但依旧非常缓慢；当轴向位置为58 mm时，材料进入了喷嘴口挤出腔体，挤出速度急剧增加。这是因为喷嘴口挤出腔体半径突然减小，挤出压力变化量突然增大，所以挤出速度也突然增大。随着挤出压力的减小，喷嘴出口处的挤出速度又趋于稳定。所以在研究挤压沉积相互作用时，只取喷嘴出口挤出腔体进行研究。

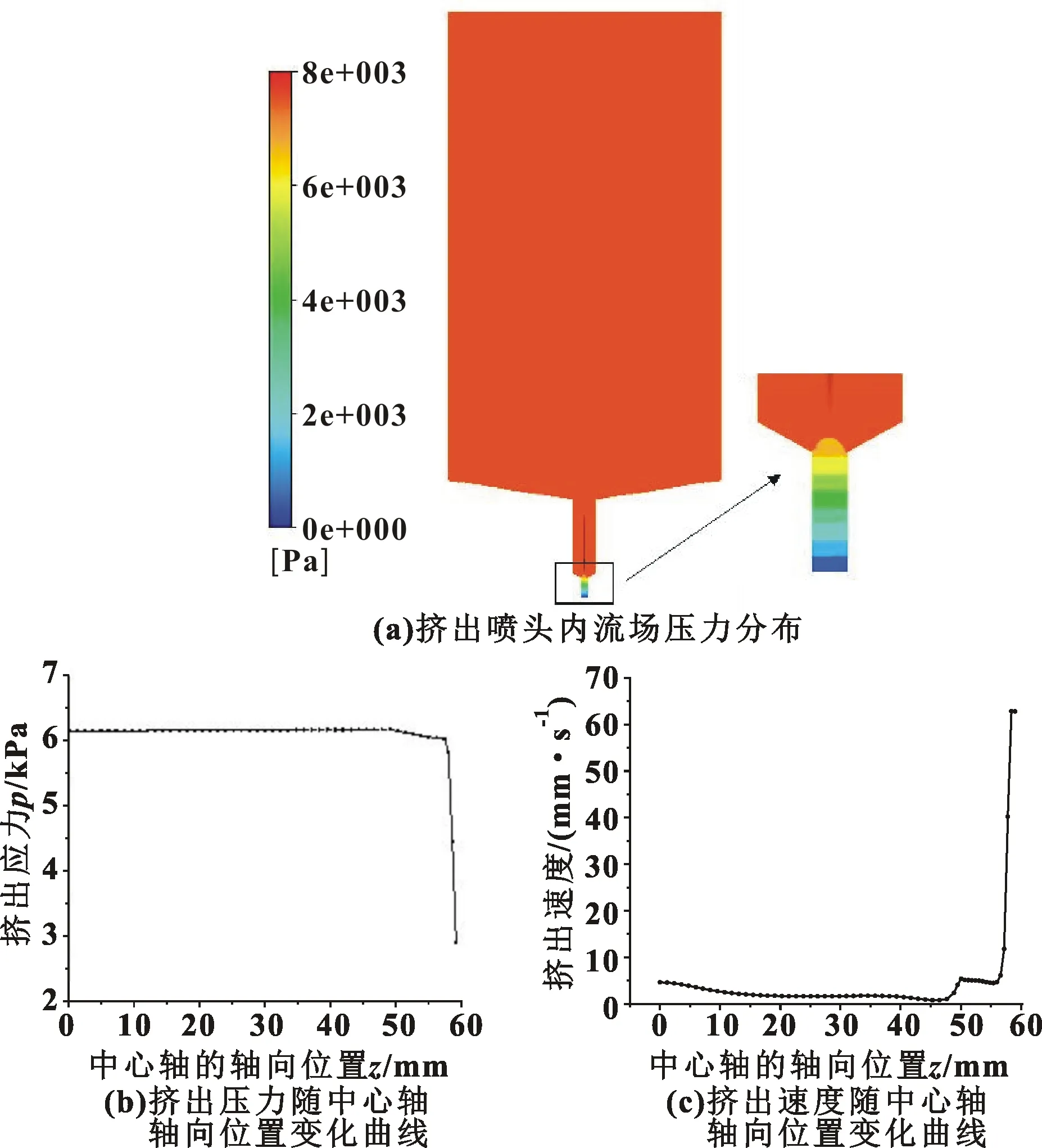
图3 挤出喷头流场特征分析

2 挤压沉积流场的数值分析

2.1 挤压沉积数值分析模型及网格划分

不适当的打印参数会造成熔丝过堆积或欠沉积，严重影响打印件的成型质量。因此，为探究挤压沉积的工艺参数对熔丝成型质量的影响，对挤压沉积进行数值仿真分析。

参考文献[14-15]，设置喷嘴为固定喷嘴，基板为移动基板，通过两者的相对运动实现熔融材料的快速打印。考虑到材料挤出后的流动问题，在喷嘴左侧增加一个长为14.5 mm的长方体，喷嘴右侧、前侧、后侧各增加长为1.5 mm的长方体作为外流场计算域，如图4所示。为减少计算量，文中只考虑熔融材料的单链挤出。其中，挤压口喷嘴内径为d、挤出口喷嘴长度为l、打印基板与喷嘴间的间隙距离为h。

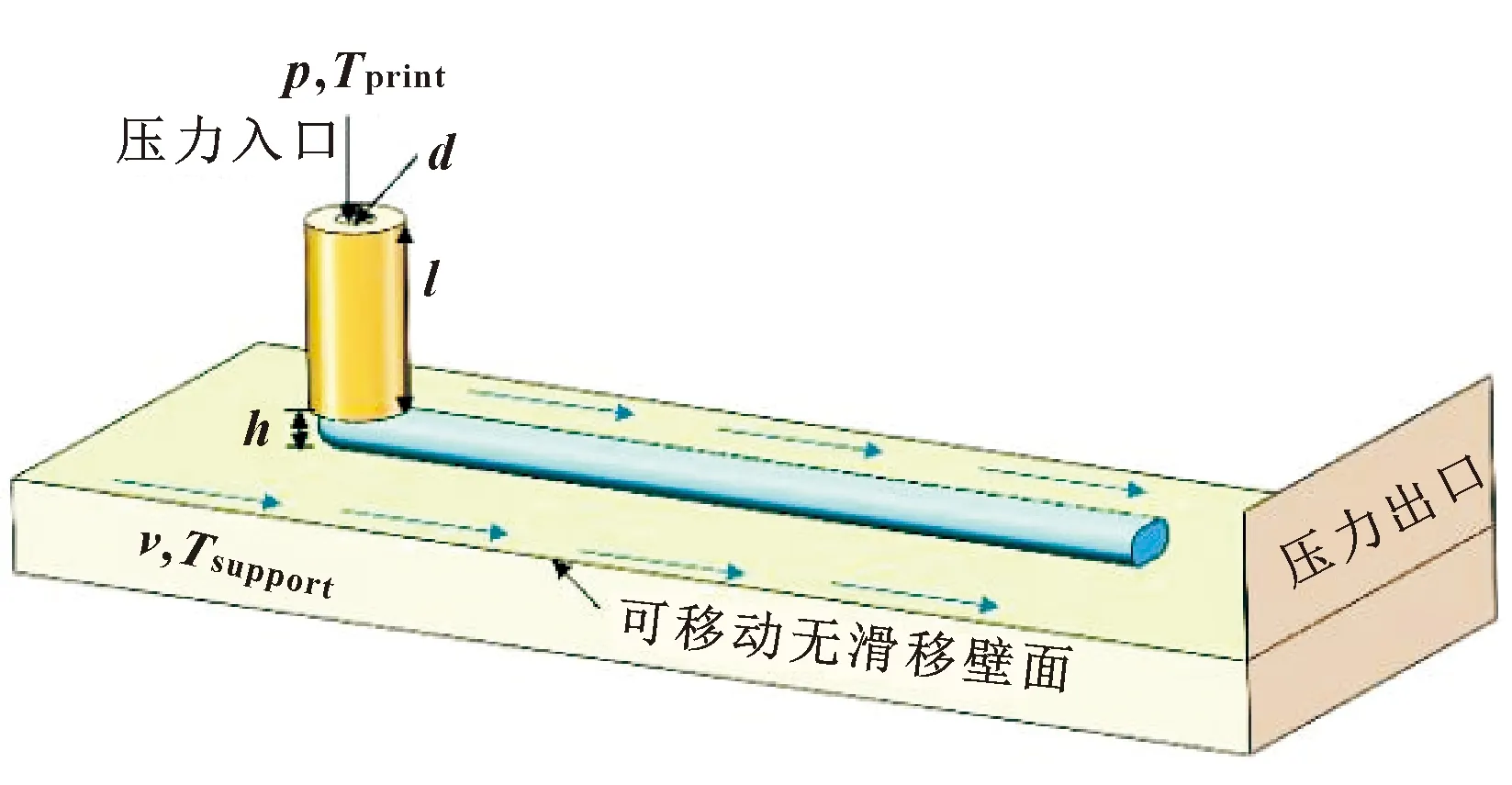
图4 铸造蜡DIW挤压沉积数值模型

控制方程采用有限体积法进行离散，采用压力求解器进行瞬态数值求解，选取Liamier模型，模型的相关参数均为默认。计算域入口采用压力入口边界条件，根据不同的喷嘴内径设置不同的入口压力，入口液相体积分数设置为1。材料与喷嘴内部接触的壁面均设置为无滑移壁面边界，基板上表面设置为可移动无滑移壁面边界条件，基板移动速度为v。基板移动方向的尾端界面设置为计算域出口，并设置为压力出口边界。外流场由长方体和圆柱体组成，几何形状规则，宜划分为六面体结构化网格，其中圆柱体部分采用O形划分法，在熔丝移动的区域进行适当的网格加密处理，网格的加密区域如图5所示。

图5 网格划分结果

2.2 工艺参数的选择与设置

根据第1.2节的假设，影响挤出沉积结果的工艺参数有打印温度、挤出速度、打印速度、间隙距离。其中，文中打印温度确定，只探究其他因素的影响。

(1)挤出速度v

由于文中采用的是气压挤出方式，挤出速度由挤出压力决定。两者关系如下：

挤压段的铸造蜡流动可以看作是不可压缩的黏性流体在竖直圆管中的层流流动，黏性流体的伯努利方程为

(5)

其中：ΔE为不可压缩的单位体积流体的平均能量损失，计算公式为

(6)

式中：λ为流体摩擦因数，该因数只与流体流动形式及管壁状况有关。

流体做层流运动时，流体摩擦因数为

(7)

将具体参数代入整理得，进出口压力差Δp与挤出速度v之间的关系式为

(8)

3D打印机的最优打印速度区间为30～80 mm/s，此研究设置打印速度为40 mm/s进行材料挤出沉积研究。因此，根据公式(8)设置不同喷嘴内径下的压力入口数值，如图6所示。

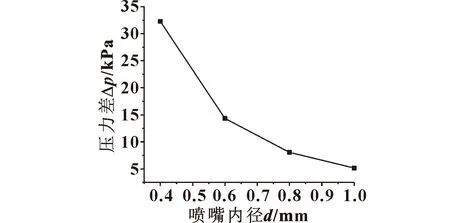
图6 平均挤出速度v=40 mm/s时，挤出压力与喷嘴内径关系

(2)打印速度/挤出速度(v/u)

当v/u<<1时，基板移动过慢，喷嘴口下的材料无法及时送出，材料易产生堆积，造成喷嘴堵塞。当v/u>>1时，基板移动过快，熔丝在打印过程中受基板摩擦力作用，会出现断丝现象。为避免熔融状态的铸造蜡材料堵塞喷嘴，在保证出丝顺畅时也提高打印效率，结合铸造蜡材料硬度较低的材料特性，取v/u值为1.0、1.25、1.5。

(3)间隙距离/喷嘴内径(h/d)

当h/d<<1时，材料堆积造成喷嘴堵塞。当h/d>>1时，喷嘴对材料无挤压作用，打印的熔丝与基板无足够的接触面积，无法黏结并沉积在基板上。在成型过程中，熔丝间通过搭接获得黏结力。为保证熔丝间的黏结，使熔丝间具有足够的接触面积，一般取h/d<1，结合铸造蜡材料黏度较低的特性，取h/d值为0.5、0.625、0.75。

综上，此研究中数值模拟计算所用工艺参数设置如表1所示。

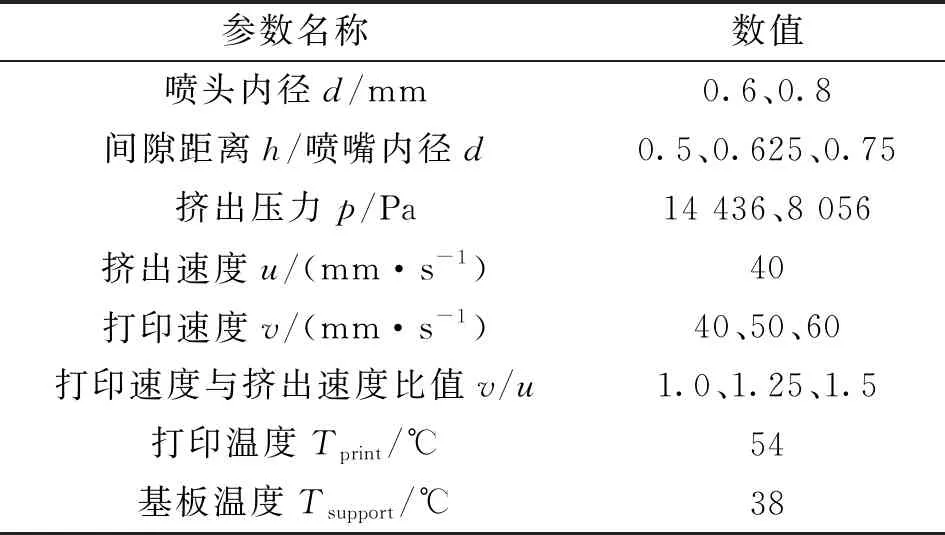
表1 工艺参数

2.3 熔丝截面几何形状的评价指标

3D打印出的熔丝的最常见的截面有圆形、椭圆形及胶囊形、长方形4种[16]，其几何特性如图7所示。胶囊形及长方形可保证熔丝之间具有足够的接触面积，保证熔丝之间的黏结力。为保证成型件的强度，熔丝之间的搭接面积越大越好，所以长方形是最理想的熔丝截面。为评估不同参数下打印熔丝的质量，采用以下2个评价指标进行评价：

图7 3D打印中常假设的熔丝理想截面[16]

(1)纵横比，即熔丝的长宽比W/H；

(2)紧凑度，即表示熔丝与熔丝之间填充空间的情况，可写为A/W·H。

3 仿真结果与分析

3.1 挤出沉积流场的基本运动规律

铸造蜡材料挤出沉积内外流场计算模型以喷嘴出口面的圆心为坐标原点，基板移动方向为X轴正方向，垂直向上为Z轴正方向。设置打印材料温度为54 ℃，在d=0.8 mm、h/d=0.5、h=0.4 mm、p=8 056 Pa、v/u=1.25、v=50 mm/s的条件下，t为0、0.027 5、0.201 5、0.301 5 s时，沉积的熔丝流形态如图8所示。可知：t=0.027 5 s时，材料和基板发生了接触，在基板和喷嘴作用下，材料截面发生膨胀，熔丝宽度大于喷嘴内径，材料在喷嘴的两侧面形成侧流，这是由于打印速度慢或间隙小的原因；t=0.201 5 s时，随着基板的移动，这种侧流对熔丝的影响消失，熔丝形状与宽度也趋于稳定；t=0.301 5 s时，沉积材料流在X轴正方向上已充分发展，熔丝形状趋于稳定。因此，后续测量熔丝截面时，也应在沉积流充分发展后再进行测量。

图8 不同时刻熔丝形态

当熔融材料流离开喷嘴与空气相接触时，流体受到的压力会随速度的变化而变化，此压力的变化是熔体变形的主要原因，此时速度为最大的影响因素。图9所示为t=0.301 5 s时材料沉积流的代表性速度流线，喷嘴出口熔丝流的平均速度为40 mm/s。可知：喷嘴内部中心轴部位材料的流动速度大于40 mm/s，近壁面速度小于40 mm/s，随着熔丝在基板上不断沉积，材料的速度逐渐趋近于基板移动速度60 mm/s。喷嘴下侧流线变宽的原因是，沉积的材料与喷嘴紧密接触，喷嘴对挤出后沉积的材料有压迫力，迫使喷嘴下方的材料横向发展发生材料聚集。当材料在此处过于横向发展时，会使得喷嘴下部相邻的熔丝叠加在一起，造成成型面不平整。

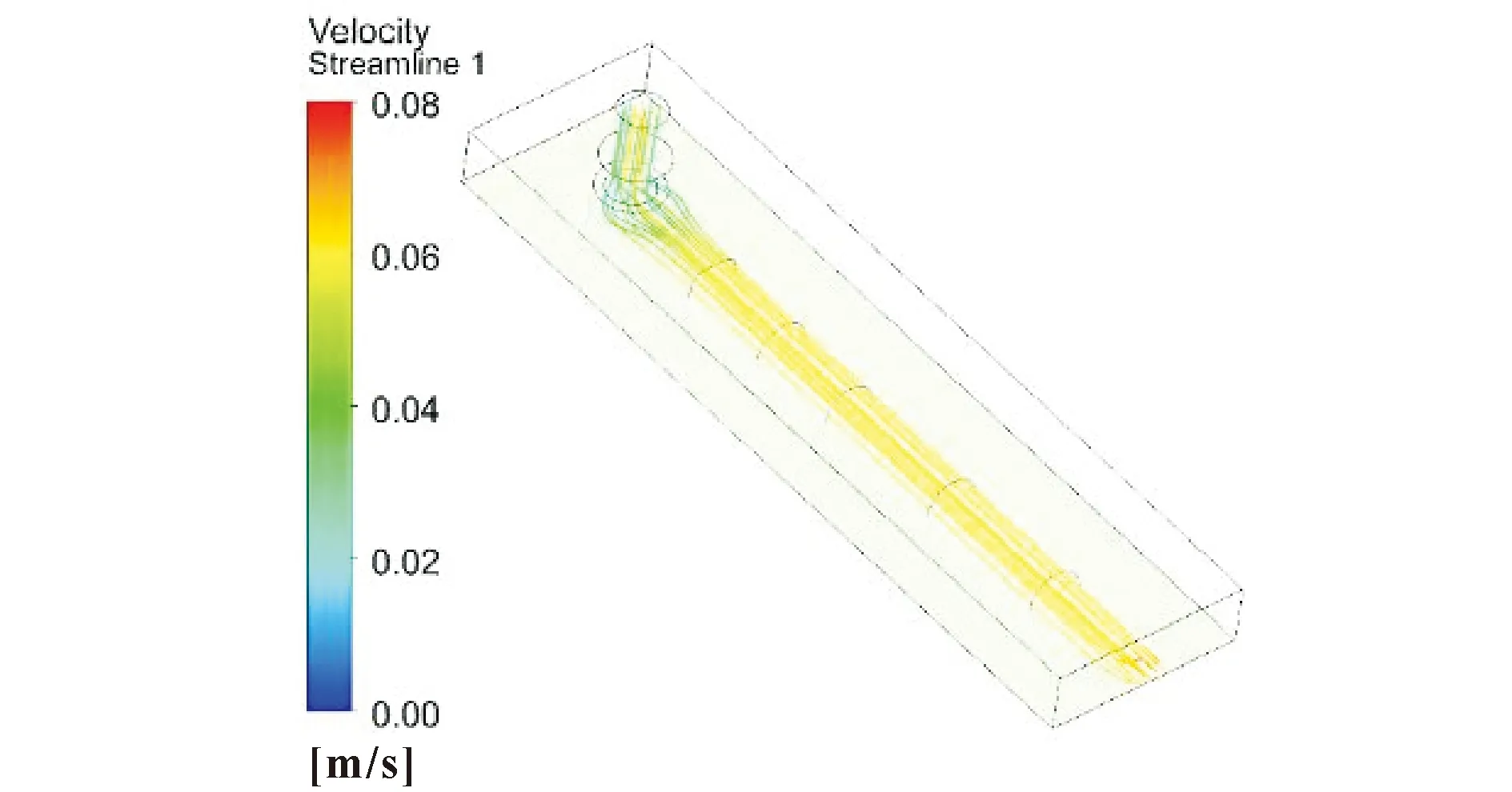
图9 t=0.301 5 s时沉积流速度流线

3.2 参数间隙距离/喷嘴内径(h/d)对熔丝几何特性的影响

选取h/d为0.5、0.625、0.75三种情况下的熔融沉积流场进行对比分析，为探究变化是否具有一致性，以0.6、0.8 mm两种内径的喷嘴为研究对象。此外，设置对应的挤出压力为14 436、8 056 Pa，此时喷嘴的平均挤出速度为40 mm/s，另设定打印速度为40 mm/s。

图10所示为不同h/d下，距喷嘴1.2 mm处的熔丝截面图。可知：随着h/d的减小，间隙距离减小，喷头对打印熔丝有更明显的挤压作用，熔丝截面由近圆形逐渐变成扁平的胶囊形，熔丝与基板的接触面积逐渐增大，黏结效果也逐渐变好。在h/d=0.5时，由于喷头的挤压作用，熔丝的宽度接近于喷嘴内径的1.65倍；在h/d=0.625时，熔丝的宽度接近于喷嘴内径的1.5倍；在h/d=0.75时，熔丝的宽度是喷嘴内径的1.25倍。此外，喷嘴内径越小这种挤压现象越明显。虽然h/d=0.75时，熔丝宽度与内径最接近，但h/d增大时，熔丝的沉积相对于喷头的打印动作滞后，熔丝与基板接触面积逐渐减小，无法与基板或下一层粘结在一起，易产生不规则的成型件，严重时会发生材料断裂的现象。h/d为0.5、0.625、0.75时，熔丝的高度均为喷嘴距基板间隙h的1.1倍左右，这与文献[15]中对聚乳酸材料的研究结果相同，当h/d<1时，熔丝高度主要受喷嘴距基板间隙的影响。

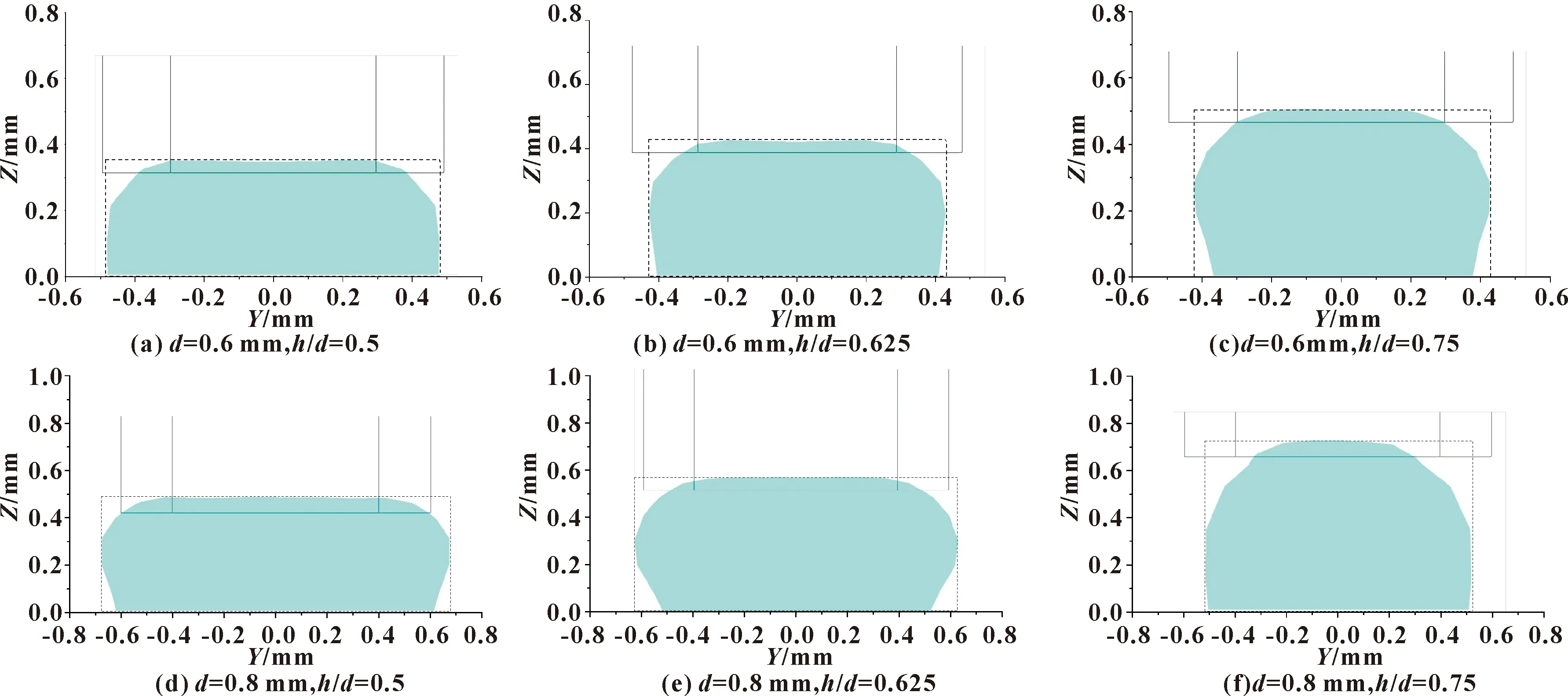
图10 v=40 mm/s时不同h/d下的截面形状

熔丝的纵横比和紧凑度随h/d变化的曲线如图11所示。可知：虽然喷嘴内径d不同时，评价指标的数值不相同，但整体趋势相同，随着h/d的增大，W逐渐减小、H逐渐增大，W/H逐渐减小，熔丝的紧凑度也逐渐减小。这说明，h/d越小，打印的熔丝间间隙越小，黏结效果越好。但h/d过小，会导致喷嘴两侧的侧流现象明显，使相邻熔丝叠加在一起。所以在保证打印质量和打印效率的前提下，应使得h/d尽量小。此外，随着h/d的变化，W的变化率小于H的变化率，证明了h/d对熔丝高度的影响更加明显。

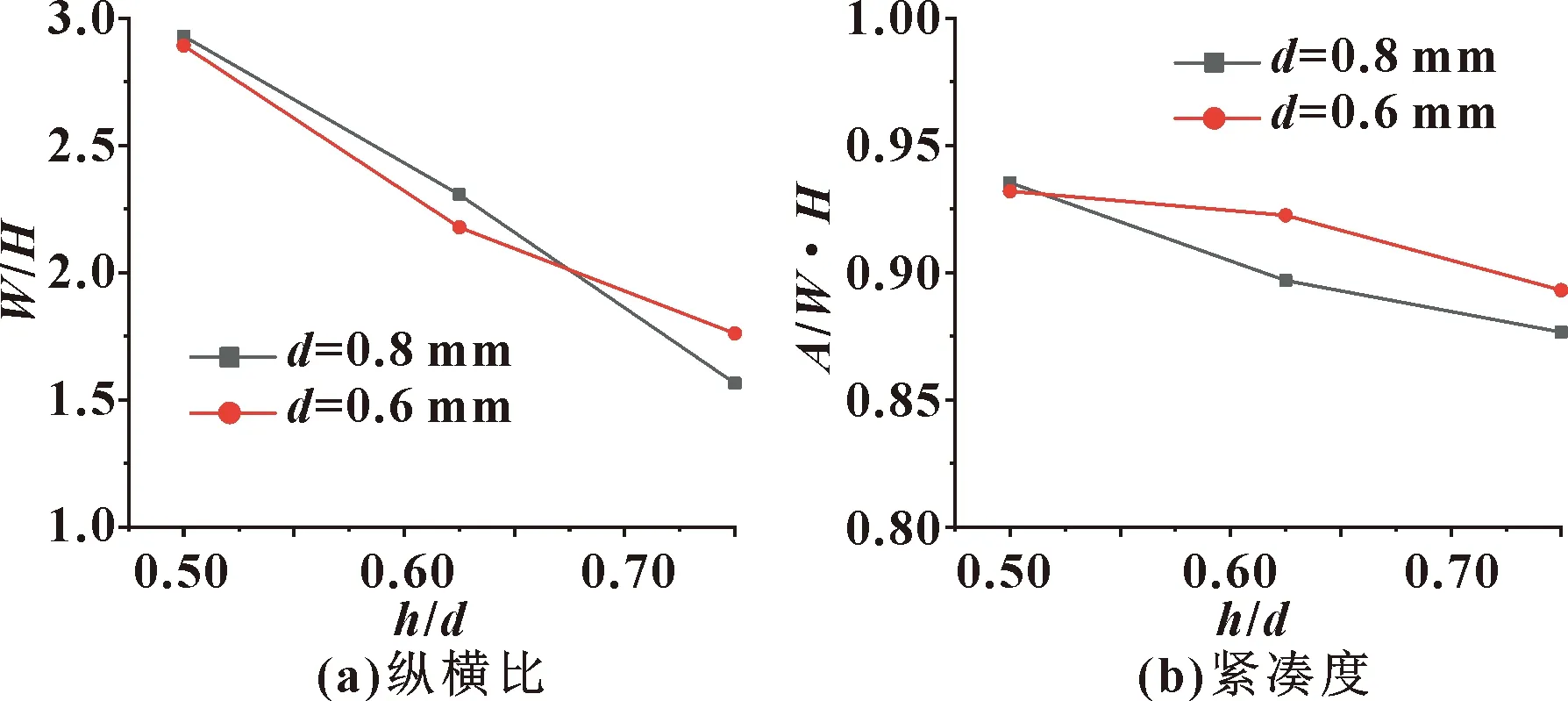
图11 熔丝的纵横比和紧凑度随h/d的变化曲线

3.3 参数打印速度/挤出速度(v/u )对熔丝几何特性的影响

选取v/u为1.0、1.25、1.5三种情况下的流场进行对比分析。为探究变化是否具有一致性，对不同间隙下的流场均进行分析。其他参数设置为喷嘴内径d=0.8 mm，挤出压力=8 056 Pa。图12所示为在不同间隙、不同速度比的情况下，距喷嘴2.2 mm处的熔丝截面。可知：随着参数v/u的变化，不同间隙下熔丝截面的变化规律基本一致；随着v/u的增大，基板对材料的作用力逐渐增大，熔丝的宽度逐渐减小，熔丝与基板接触面积逐渐减小，黏结效果变差，熔丝截面由扁平的胶囊形状逐渐演变成近圆形。在v/u为1.0、1.25时，v/u较小，材料会在基板上有过堆积现象，此时的熔丝横截面为类胶囊形；随着v/u的增大，在v/u=1.5时，熔丝截面的高度略小于v/u为1.0、1.25时的截面高度，但熔丝截面的宽度以10%～15%的比例减小。h/d越小，熔丝宽度随v/u增大而减小的效果越明显。当v/u继续增大，熔丝截面逐渐变形为圆形，熔丝间的黏结面积变小，熔丝间不易粘结。v/u的变化对熔丝宽度W的影响较大，对熔丝的高度H几乎无影响。

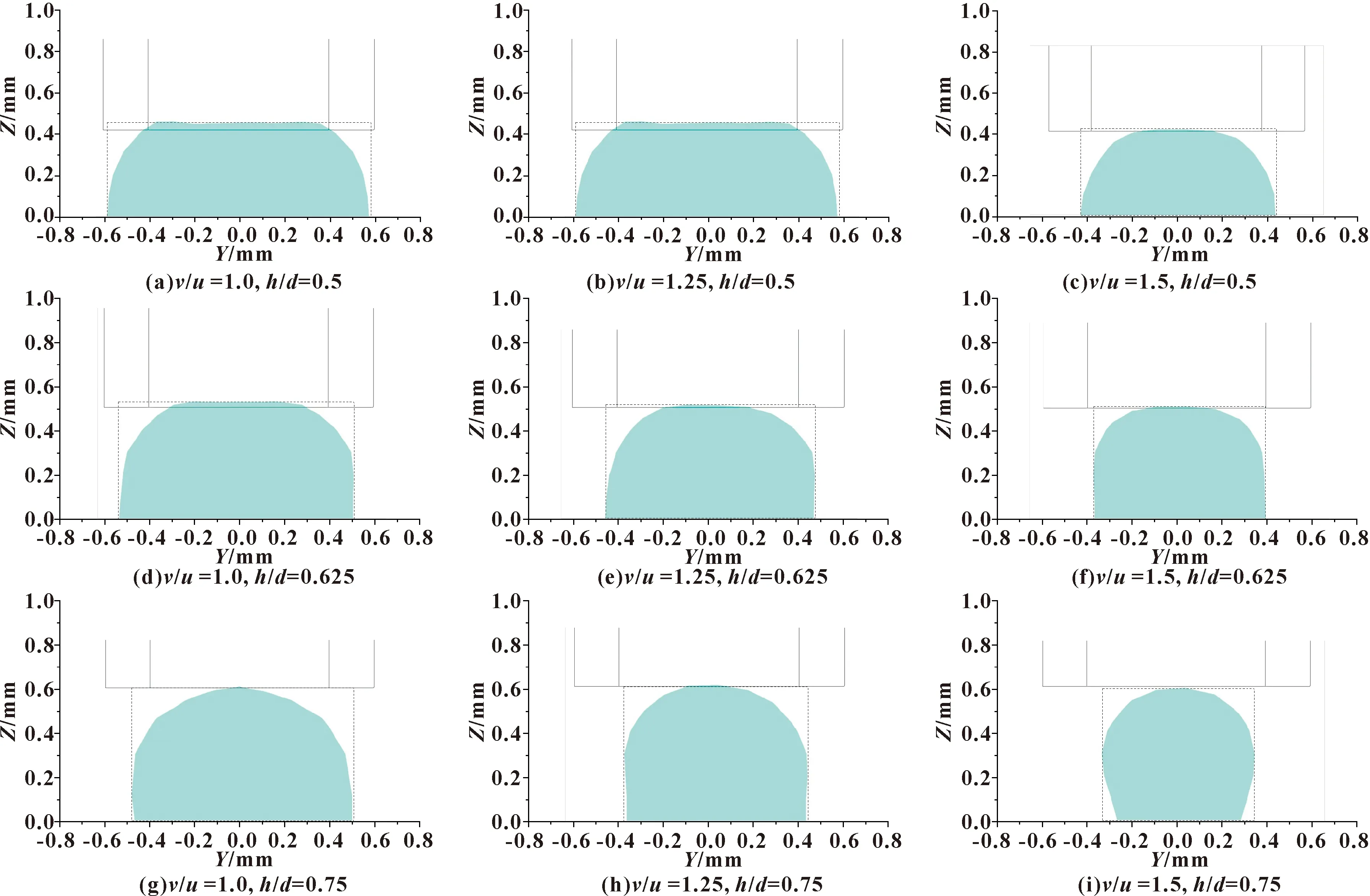
图12 d=0.8 mm时不同工况下测得的熔丝截面

图13所示为纵横比H/W、紧凑度A/W·H随v/u的变化折线图。可知：随着v/u的增大，纵横比W/H呈线性减小，但随着h/d的增大，纵横比W/H随v/u的变化越缓；h/d=0.5时，纵横比W/H随v/u变化曲线的斜率最大，h/d=0.75时，纵横比W/H随v/u变化曲线的斜率最小。这是因为h/d越大，喷头挤压作用越小，熔丝的高度变化越小；h/d为0.5、0.75时，随着v/u的增大，紧凑度先增大后减小；h/d=0.625时，随着v/u的增大，紧凑度先减小后增大；此实验没有得到紧凑度随v/u清晰的变化趋势。这是由于材料在喷嘴两侧侧流的影响。但从数值上看，在保证打印效率的前提下，v/u为1.25时打印的熔丝较好。

图13 纵横比和紧凑度随参数v/u的变化曲线

4 实际打印结果验证

本文作者利用搭建的3D打印平台(如图14所示)，对铸造蜡材料进行了挤出沉积实验，以喷嘴d=0.8 mm为例，设置喷嘴加热温度为54 ℃、平均挤出速度为40 mm/s、基板温度为35 ℃、3D打印机打印速度为40 mm/s。由于铸造蜡材料采用气动方式挤出，通过调节挤出压力，可使材料竖直挤出，挤出的压力设置为213.74 kPa左右时，可满足实验要求。材料挤出均匀后，再利用相机对挤出材料进行快速拍摄，计算出打印材料的实际平均挤出速度。

图14 铸造蜡热辅助DIW打印平台

通过改变G代码，分别设置首层打印高度为0.4、0.5、0.6 mm，在不同间隙比下进行打印实验。待熔丝冷却后，截取小段熔丝进行观测，在光学显微镜下观测熔丝截面并测量尺寸。结果表明，数值模拟和实际打印实验的沉积熔丝截面轮廓及几何特性的变化趋势具有很好的一致性，如图15所示，但截面的实际尺寸与数值模拟的结果存在一定的偏差，具体数据如表2所示。

图15 不同工况下实际打印熔丝的截面轮廓

表2 数值模拟与实验结果对比

图16所示为上述实验条件下数值模拟、实验及理想截面长方形和胶囊形的纵横比随h/d的变化趋势。可以看出：数值模拟比理想截面可以更准确地预测熔丝的几何特性。

图16 数值模拟、实验及理想截面纵横比的比较

文中的仿真中只考虑了绝热情况下熔丝挤出的情况，未考虑材料的凝固效应，且在实际打印过程中物理场复杂，非牛顿流体效应、非均匀挤出及材料与基板之间的传热等多种因素均会导致数值模拟结果与实验之间存在差异。但数值模拟能够以合理的一致性模拟出实际打印熔丝截面的大部分几何特征，且整体误差控制在10%以内，可以接受。所以该数值模型可适用于低黏度流体，尤其是铸造蜡的3D打印熔丝的几何形状估计，可为实际打印中准确控制熔丝形状提供参考。

5 结论

本文作者首先建立了铸造蜡DIW过程中挤出喷头内流场的数值模型并分析了流场特性，根据喷头内流场特性选取了喷嘴口挤出段进行挤出沉积段研究，建立了铸造蜡DIW挤压沉积流场的计算流体动力学模型，通过数值分析和实验的方法探究了工艺参数挤出压力、喷头半径、喷头距基板距离及打印速度对挤出熔丝成型及截面几何特性的影响，并采用纵横比和紧凑度对所得熔丝截面进行评价。主要结论如下：

(1)通过实验验证，验证了所建立的挤出沉积的数值模型可以实现在不同挤出压力、喷头半径、喷头距基板距离及打印速度工艺参数下对熔丝几何截面长宽及几何形状的准确性预测，还可为DIW仿真中准确化简截面形状提供参考；

(2)在铸造蜡DIW过程中，设置普通速度比即v/u=1.0，选择间隙h/d=0.625时，熔丝的打印结果最优；设置速度比v/u=1.25，选择间隙h/d=0.5时，熔丝的打印结果最优；设置速度比v/u=1.5，选择间隙h/d=0.625时，熔丝的打印结果最优。

由于文中的数值模型假设为绝热条件，模型预测的熔丝几何特性与实际结果存在偏差。虽然该误差在可接受范围内，但仍然有优化的空间。因此在后续的研究中，可以进一步考虑温度对熔丝成型的影响，从而提高数值模型预测的准确度。