室内走廊环境毫米波OAM信道特性分析与统计建模
廖 希 何昌文 王 洋* 万杨亮 陈前斌 张 杰
①(重庆邮电大学通信与信息工程学院 重庆 400065)
②(95696部队 重庆 400030)
③(谢菲尔德大学电子电气工程系 谢菲尔德 S10 2TN,UK)
1 引言
因轨道角动量(Orbital Angular Momentum,OAM)模态间正交性和完整性优势,OAM复用能够在有限信道资源上实现信息高质量和大容量传输,携带OAM的电磁涡旋通信技术能潜在地增加无线通信链路的系统容量和频谱效率[1–7],被视为第6代无线通信网络的关键技术之一。构建准确的涡旋信道模型是涡旋通信系统设计、性能评估、网络部署和优化的首要任务。
为了实现电磁涡旋通信系统,亟需在准确刻画OAM信道特性基础上,建立能够复现涡旋信号波前结构和幅值特性的OAM信道模型。建模实质是表征拓扑荷和传播距离等因素对涡旋信号幅度与相位的影响。现有的OAM信道模型主要包括自由空间传播模型[8]、利用螺旋相位因子的涡旋信道模型[9]、基于电磁场理论的涡旋信道模型[10]、基于拉盖尔-高斯模的涡旋信道模型[11],以及基于镜面反射的多径信道模型[12]。文献[8]建立了基于失调均匀同心圆形阵列的自由空间涡旋信道模型,并对多模式复用OAM多输入多输出(Multiple Input Multiple Output,MIMO)系统的频谱效率和能量效率进行了研究,结果表明频谱效率和能量效率优于传统MIMO系统。文献[13]建立了基于拉盖尔-高斯理论的自由空间涡旋信道模型,研究了信道传递函数、时域函数及路径损耗,结果表明与自由空间传播模型相比,提出模型能够更准确地刻画涡旋信道特性。文献[14]建立了基于螺旋相位因子的多天线电磁涡旋信道模型,利用该模型分析了最佳相位条件下的涡旋信道容量,结果表明相比传统MIMO系统,多天线电磁涡旋系统具有更高信道容量。上述研究表明,构建OAM信道是研究涡旋波传播特性以及进行OAM通信系统性能评估的前提[15]。
现有研究存在以下不足:一是在自由空间传播环境中构建的涡旋信道,仅考虑了路径损耗对涡旋信号的影响,而对涡旋信号相位结构变化的研究还不足;二是OAM通信系统更多是部署在多径环境中,自由空间传播环境下建立的涡旋信道不能准确地刻画出多径环境对涡旋信号的影响。针对多径传播,Yan等人[16]分析、仿真和测量了两径OAM信道(1条直射径和1条镜面反射径)引起的信道内和信道间串扰,结果表明OAM信道模态数越大,信道内串扰和信道间串扰越严重。基于光学射线理论,文献[17,18]通过计算传播距离,建立了OAM-MIMO通信系统的两径信道模型和峡谷环境下的6径信道模型,结果表明多径效应引起的相位畸变和信道串扰随着模态数增大而增大,模态数较小的涡旋信号可以获得更好的传输增益。Liang等人[19]构建了混合正交频分复用通信系统的稀疏多径信道模型,该模型包含1条直射径、1条1次反射径、1条2次反射径和1条3次反射径,能够描述简单通信场景下的涡旋信道特性。然而,OAM通信技术被期望应用到“室内、城区、隧道、高速铁路”等热点与特殊场景中,复杂多样的建筑物引起的多径干扰会改变波前相位,破坏涡旋波的形态,致使OAM信道呈现出复杂性、特殊性和时变性等特点。现有的自由空间传播信道模型、两径信道模型、稀疏多径信道模型尚不能准确刻画真实场景下OAM信道多径特性,因此有必要针对实际应用场景中多径传播机制构建准确的OAM信道模型。
信道建模方法主要有确定性建模法和统计性建模法[20]。现有的OAM信道建模本质上是确定性建模方法,核心思想是在已知传播环境详细电磁参数前提下,利用电波传播理论或光学射线理论来预测传播距离,因此严格依赖于传播场景及建筑物的分布,不适用于复杂的室内环境。在室内环境,毫米波能实现高速通信,但毫米波OAM信道特性尚未明确,尤其是波前相位和幅度随多径传播条件、模态数和传播距离等影响因子的变化规律,毫米波OAM信道统计性模型尚无。
针对以上问题,本文开展走廊场景毫米波OAM信道特性分析和统计建模研究,为室内毫米波OAM通信链路与系统仿真提供涡旋信道基础数据和统计模型。首先,在走廊场景中建立基于均匀圆形天线阵列(Uniform Circle Array, UCA)的OAM辐射传输系统;其次,基于光学射线理论推导视距(Line-of-Sight, LoS)和非视距(Non-LoS, NLoS)传播条件下的信号传播距离,结合UCA辐射理论构建OAM信道理论模型;然后,根据多径传播条件下毫米波OAM信道的波前相位和幅度统计值,结合拟合误差确定统计模型及参数;最后,研究不同传播条件、模态数和传播距离下波前相位与幅度衰落特性。
2 走廊传播环境
矩形长直狭窄走廊环境由地面、天花板和两面墙壁组成,分别是花岗岩、石膏板和白色瓷釉面砖材料,反射系数用Γ1,Γ2和Γ3表示。地面与天花板间距为3 m,两面墙壁间的距离为2.5 m,长度为3 m。图1(a)和图1(b)分别构建了LoS和NLoS传播条件的OAM辐射传输系统。考虑到天线阵列能够在所有频率范围内产生不同模态的涡旋波,系统模型的发射端是由N个阵元组成的UCA天线阵列,阵元用n表示,0≤n ≤N −1,接收端使用单个天线。图1(a)中收发端天线之间的第1菲涅尔区内不存在障碍物,存在1条直射径。图1(b)中存在1个几何尺寸略大于发射阵列尺寸的障碍物,导致仅有非视距信号。本文假设发射端UCA的中心O与接收端天线的水平距离为D,UCA阵列半径为Rt,阵列中心O距地面、天花板、墙1和墙2的距离分别为h1,h2, h3和h4。
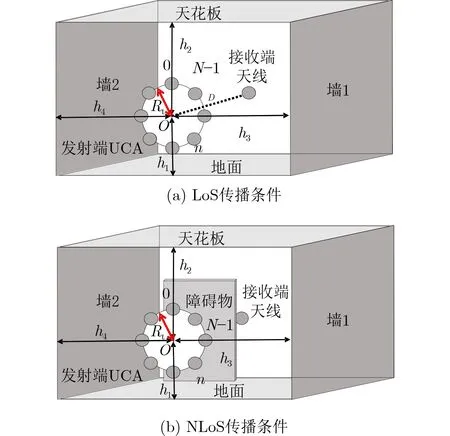
图1 OAM辐射传输系统
3 涡旋信道模型
本节基于光学射线理论建立了走廊场景LoS和NLoS传播条件的多径模型,推导传播路径的距离,基于UCA辐射理论建立OAM信道模型。
3.1 传播模型
为了更加直观地体现多径传播,图2(a)和图2(b)分别给出了狭窄走廊环境下LoS和NLoS传播条件多径传播模型的侧视图和俯视图。涡旋信号在走廊环境中传播时会发生直射、反射和散射等多径传播机制,使得接收端接收到的是来自不同路径涡旋信号的叠加信号。为了便于分析,本文只考虑直射传播和反射传播机制,且因3次及以上反射路径的信号强度过低,只考虑1次与2次反射路径。
图2(a)为LoS传播条件下多径传播模型的侧视图,传播路径包含1条直射路径,1条地面反射路径GR、1条天花板反射路径CR、2条墙壁反射路径WR、1条地面与天花板反射路径GC、2条地墙反射路径GW、1条天花板与地面反射路径CG、2条天花板与墙壁反射路径CW、2条双墙反射路径TW、2条墙地反射路径WG、2条墙壁与天花板反射路径WC等16条反射路径。图2(b)为NLoS传播条件下多径传播模型的俯视图,收发天线间不存在直射路径,只包含了16条反射路径。

图2 走廊环境多径传播模型

以此类推,可以推导出CR, WR, CG, CW,TW, WG和WC反射路径的传播距离。
3.2 信道模型
收发天线静止不动时传播信道传递函数可以表示为

其中,K表示多径数,ak, τk, θk分别表示幅度、传播时延和相位序列。对于静态传播信道,幅度和相位可以通过电场强度Ek(dn)获得,dn为不同路径下第n个阵元到观测点的距离,所以式(5)可以表示为
由此,可以依次推导出CR, WR, CG, CW,TW, WG和WC路径上的电场强度,最终获得LoS和NLoS传播条件的OAM信道传递函数。
4 结果与分析
本节基于OAM信道模型研究不同传播条件下毫米波频段涡旋波波前相位和幅度特性。以相位和幅度的统计结果为拟合目标,使用不同的概率统计模型进行拟合,采用均方根误差(Root Mean Squared Error, RMSE)作为评估指标,验证统计模型的准确性,并且对模型进行统计性分析。具体地,使用均匀分布描述不同传播条件下的OAM信道波前相位;使用莱斯因子确定符合的概率分布模型,利用Nakagami-m模型的衰落因子m确定不同传播条件下的幅度分布。
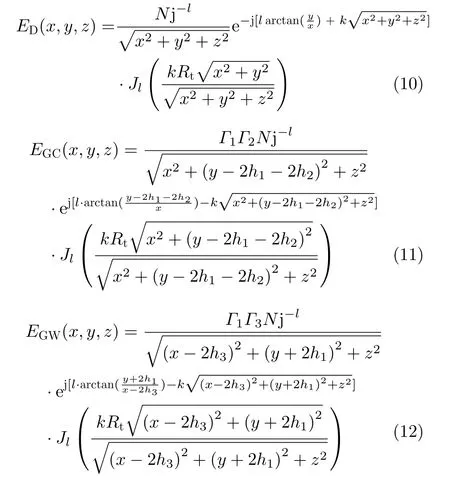
假设工作频率为30 GHz,阵列半径为0.02 m,由于阵元尺寸和阵列半径的限制,将阵元数设置为8,中心O与地面、天花板和两面墙壁的距离分别为1.5 m, 1.5 m, 1.2 m和1.3 m,地面、天花板和墙壁的反射系数分别为0.7, 0.91和0.75[24]。仿真采用的软件为MATLAB,主要参数如表1所示。
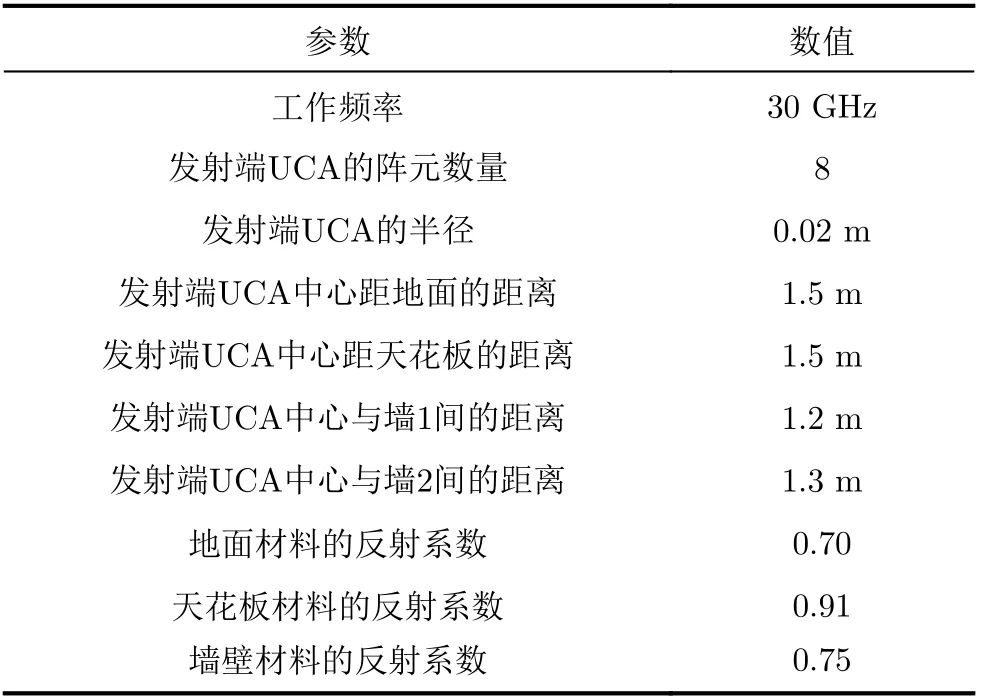
表1 仿真参数设置
4.1 波前相位
由文献[13]可知,OAM通信系统适用于短距离传输,因此设两个观测面距发射端UCA的距离分别为0.4 m和1 m,大小均为0 .4 m×0.4 m,模态数l分别为1, 2, 3。
图3是OAM多径信道的波前相位,图3(a)、图3(c)和图3(e)的观测面距发射端UCA的距离为1 m,图3(b)、图3(d)和图3(f)的观测面为0.4 m,图3(a)和图3(b)是直射径传播,图3(c)和图3(d)是3条传播路径(1条直射径和2条1次反射径),图3(b)和图3(e)是5条传播路径(1条直射径和4条1次反射径)。结果表明,相比1条直射径传播,多条路径传播的OAM信道相位发生了畸变,模态数越高,畸变越严重;对比不同传播路径,相同传播距离传播路径越多,相位畸变越严重,这是因为多径传播引起的信道间和信道内串扰,致使相位产生畸变,且随着模态数增大和传播路径增多而增大。对比不同传播距离,相同传播条件传播距离越远,相同观测平面内的信道相位畸变越严重,辨别OAM信道模态数的难度越大,这是由OAM波的发散性导致的。
基于图3的结果,对不同模态的OAM相位进行统计,由于1, 2, 3模态的概率密度分布相似,本文只给出模态数为1和2的相位分布,如图4所示,其中直方图为概率分布。结果表明信道相位符合均匀分布,概率分布表示为

图3 不同模态的OAM信道波前相位
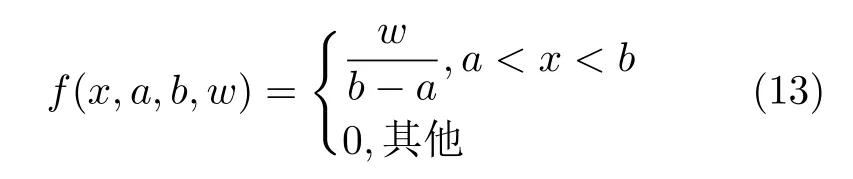
其中,w是调整拟合曲线的参数,a和b分别为数轴上的最小值和最大值。在表征波前相位分布中,a可以取0°,b可以取360°。图4中实线为均匀分布的拟合结果。
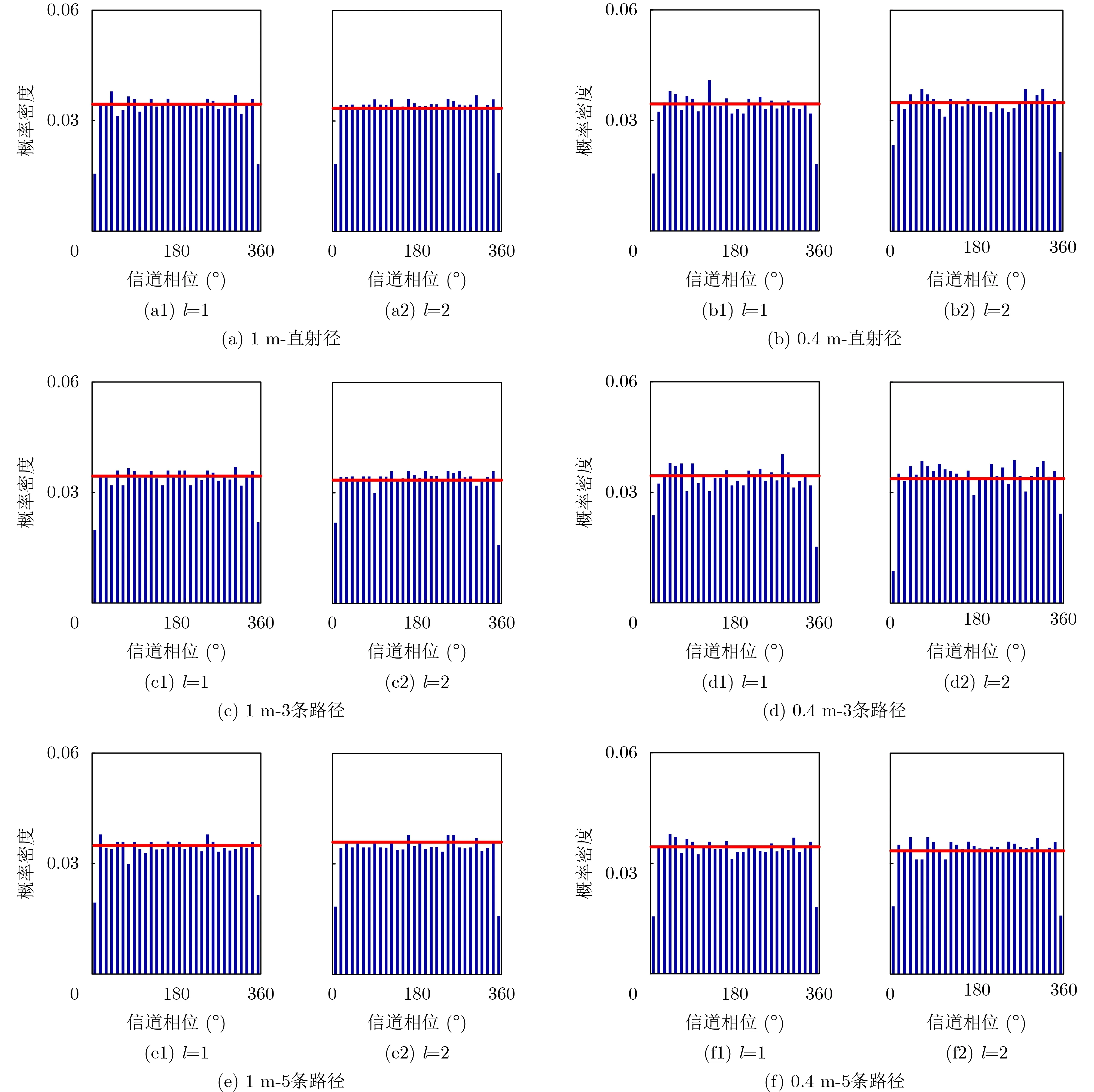
图4 OAM信道相位的统计概率及均匀分布拟合结果
不同传播条件下的均匀分布最佳拟合参数以及拟合误差如表2所示。结果表明波前相位分布值与均匀分布间的拟合误差RMSE约为0.5%,不同观测距离间的拟参数w差距在0.5以内,这说明均匀分布可以准确地表征OAM多径信道的波前相位统计特性。
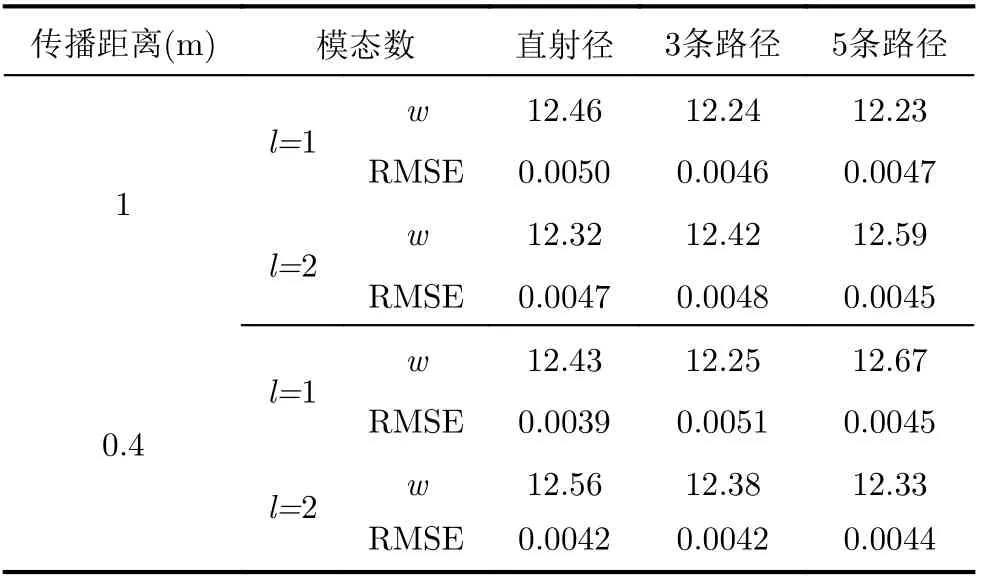
表2 最佳拟合参数w与拟合误差
4.2 信道幅度
为了获得多径传播条件下OAM信道幅度特性,图5给出了不同传播条件下不同传播距离的OAM信道幅度的变化规律,其中图5(a)为直射径传播,图5(b)为视距传播(1条直射径、4条1次反射径和12条2次反射径),图5(c)为非视距传播(4条1次反射径和12条2次反射径)。
从图5可以观察到,直射径和LoS传播条件下,OAM信道幅度随模态数增大而逐渐减小,相同传播距离时模态数越大,信道幅度衰减也越大;当传播距离小于0.4 m时,直射径和LoS传播条件的OAM信道幅度的动态变化范围为0~50 dBmV/m, NLoS传播条件的信道幅度仅仅在0~10 dBmV/m间波动,这是因为NLoS传播条件下,反射径对接收信号的贡献远远低于存在直射径的传播情况;当传播距离大于0.4 m时,直射径传播的信道幅度发生了平滑衰减,LoS和NLoS传播条件的信道幅度在0~10 dBmV/m间剧烈波动,这是因为OAM波的发散性使远距离传输时相位畸变严重,导致幅度剧烈波动,多径效应也导致远距离传输的信道幅度衰减增大。
LoS传播条件下,直射径功率与反射径功率之比定义为莱斯因子,表示为K,不同模态OAM多径信道的K值随传播距离的变化规律如图6所示。从图6可以观察到,当传播距离较小时(小于0.4 m),K值在0~20 dB之间波动,且由图5(a)和图5(b)可知,LoS传播条件下的信道幅度衰减与只有直射径传播的信道幅度衰减情况相似,此时直射径信号是接收信号中的主导分量,信道幅度分布可能接近于莱斯分布。当传播距离较大时(大于0.4 m),K值明显小于0 dB,且由图5(b)和图5(c)可知,LoS传播条件下的信道幅度衰减与NLoS传播条件下的信道幅度衰减情况相似,此时反射径信号是接收信号中的主导分量,信道幅度分布可能接近于瑞利分布。因此,本文提出利用Nakagami-m分布模型描述不同传播条件的OAM信道幅度分布。
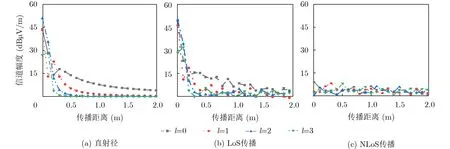
图5 OAM信道幅度

图6 莱斯因子随传播距离变化图
基于图5(b)和图5(c)的涡旋信号幅度,统计不同模态下较大传输距离(2 m)时OAM多径信道幅度的概率值,使用Nakagami-m分布模型描述信道幅度分布,根据衰落因子m判断信道幅度所服从的概率分布:
(1)m=1时,Nakagami-m分布退化为瑞利分布;
(2)m>1时,Nakagami-m分布与莱斯分布接近。
Nakagami-m分布模型表示为

图7给出了LoS和NLoS传播条件下的OAM多径信道幅度分布,直方图为信道模型统计值,实线为Nakagami-m分布拟合值。拟合参数及拟合误差如表3所示。
从图7和表3可以看出,信道幅度概率分布与Nakagami-m概率分布模型有较好的拟合程度,且衰落因子m都接近1,因此LoS和NLoS两种传播条件下的信道幅度概率分布都接近于瑞利分布。LoS传播条件下,σ随着模态数增大而减小,即多径信号平均功率减小,接收信号中直射径占主导地位;统计值与拟合值间的RMSE随模态数增加而减小,高模态的拟合误差低至0.6%,这说明瑞利分布模型能够较好地刻画出信道条件差的OAM 多径信道幅度变化;与LoS传播条件相反,NLoS 传播条件下σ随模态数增大而增大,说明信道幅度的衰减随模态数增大而减小,多径传播有利于高模态OAM多径信号接收。此外,信道模态数相同时,LoS传播条件下σ始终大于NLoS传播条件下的σ,这说明多径传播使信道幅度衰减更加严重。

图7 OAM多径信道幅度的统计概率及拟合结果
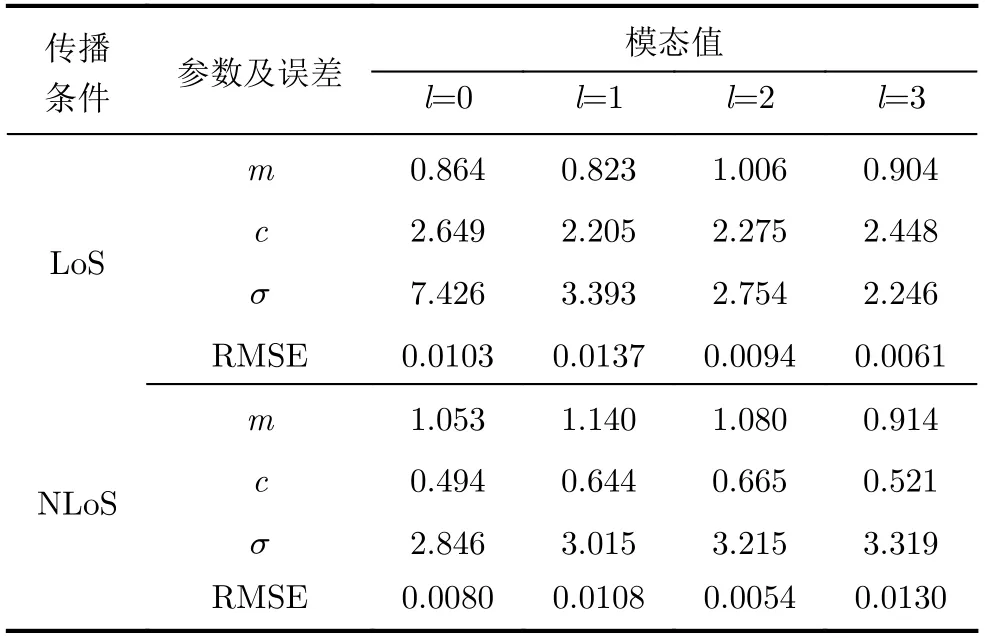
表3 Nakagami-m分布拟合参数和拟合误差
统计短距离(0.4 m)LoS传播条件下的OAM多径信道幅度概率值,使用Nakagami-m分布模型描述信道幅度值分布,幅度值概率分布和拟合结果分别如图8所示。直方图为幅度的概率分布,实线为Nakagami-m分布的拟合曲线。拟合参数及其误差如表4所示。
图8和表4表明,信道幅度概率分布与Nakagamim分布模型有较好的拟合程度,且m都大于1,因此LoS传播条件下,较短距离传播时的信道幅度概率分布更接近于莱斯分布。拟合误差RMSE在1%~1.5%范围内,σ随着模态数增大而增大,说明LoS传播条件下短距离传播时,OAM 信道幅度的衰减随模态数增大而减小。
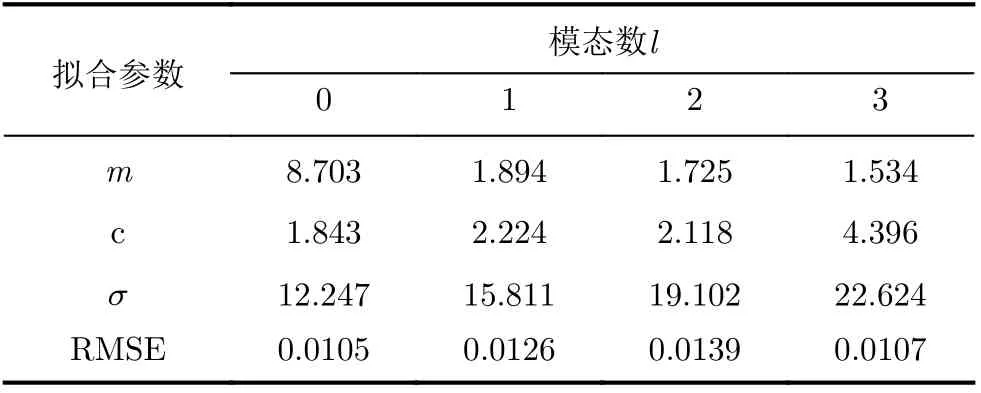
表4 LoS传播条件Nakagami-m分布拟合参数和拟合误差
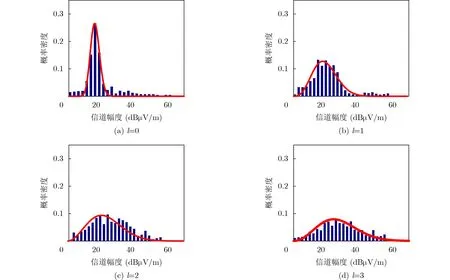
图8 短距离传播LoS条件下的OAM信道幅度统计概率及拟合结果
5 结束语
本文针对走廊环境下的毫米波OAM通信,提出了一种基于Nakagami-m分布的多径信道建模方法,研究了模态数、传播距离和传播条件对相位结构与信道幅度的影响。结果表明相位波前结构分布与模态数、观察距离和多径传播条件密切相关,且服从均匀分布;较大距离多径传输致使相位畸变严重,信道幅度波动较大,衰减较大,信道幅度分布接近于瑞利分布;较小距离LoS传播时,信道幅度分布接近于莱斯分布,较小模态数的涡旋信号有利于增大接收端的接收功率。本文基于Nakagamim分布拟合的长距离和短距离OAM多径信道参数,可以用于描述不同模态数、不同传播距离和不同传播条件下的 OAM 多径衰落信道特性,为室内场景毫米波OAM通信系统设计与性能评估提供了有用信息。

