基于Arnold变换的量子图像混沌加密方法

石金晶 陈 添 陈淑慧* 李 琴 施荣华

①(中南大学计算机学院 长沙 410083)

②(湘潭大学计算机学院 湘潭 411105)

1 引言

图像传输不仅携有通信者之间的敏感信息，还含有不可估量的样本数据，如何可靠有效地进行图像传输便成为网络通信中的重点研究方向之一。基于量子叠加和量子纠缠等特性，很多杰出的量子算法[1–4]被提出，从而威胁到大多基于数论的经典密码算法的安全性。因此在当今信息飞速发展的时代，设计出更加安全有效的图像密码算法至关重要。

早在2013年，Zhou等人[5]结合经典密码和量子几何转换首次提出了量子图像密码的概念，为图像加密提供了新的研究方向。目前为止，关于量子图像加密算法的研究方式主要分为两种：一种是基于量子仿射变换和随机旋转操作[6–8]来更改图像的像素位置和像素值以模糊明文图像；另一种则处于较新的研究领域，即基于混沌系统生成的混沌系数来控制量子逻辑门[9]。虽然后者发展不久，但在密码研究方面具有潜在的优势：根据混沌系统生成的混沌系数(随机数)使每次加密对象的处理参数均不同，从而比固定参数的加密方法更能抵抗重放攻击。

2013年Yang等人[10]首次将双重随机相位编码技术引入到量子密码研究当中，并结合量子傅里叶变换提出了量子图像加密算法。哈密顿量对初始参数的超敏感性可使量子系统呈现出混沌力学行为[11]，2013年Abd等人[12]便利用Goggin等人[13]提出的量子逻辑斯蒂(logistic)映射，设计了一种新的经典彩色图像加密方案，进一步增加了密钥空间与算法性能。接下来，为了改进经典图像加密算法的安全性及图像处理效率，Tan等人[14]利用陈氏超混沌系统[15]和量子傅里叶变换实现了量子彩色图像加密算法，该算法计算复杂度为O(n2)，相比于经典图像加密算法具有指数级优化。2016年Yang等人[16]通过构建1维量子细胞自动机实现了量子图像加密方案，在安全性和鲁棒性方面具有一定优势。2018年Liu等人[17]基于量子Arnold变换和量子比特随机旋转提出了双重量子图像加密方案，由量子傅里叶变换实现的量子比特随机旋转操作使得其计算复杂度为O(n2)。同年，Zhou等人[9]结合5D超混沌系统和量子交换操作来增强量子彩色图像加密方案中的随机性和不可预测性，相比于经典图像加密方案在有效性和安全性方面具有一定的改善。鉴于当前实际量子资源的稀缺性，为进一步降低计算复杂度，2018年Wang等人[18]使用小波变换存储图像的低频部分来缩小图像，旨在提高处理图像效率并降低计算复杂度到O(n)。但是，该方法由于不能完全解密出原始图像，因此不适用于要求高清晰度解密图像的场景当中。2019年，Khan等人[19]提出一种基于置换的特殊线性变换应用于量子图像加密算法，能够抵御一定程度的密钥攻击。2020年，Liu等人[20]基于位平面排列和正弦逻辑映射提出了一种新的量子图像加密算法，其加密图像有着更高的信息熵，但难以抵抗高裁剪攻击的情况。2021年，Liu等人[21]在此基础上采用Arnold变换和logistic映射进一步优化了加密图像的信息熵和抗噪声攻击性。可见，优化算法的安全性、计算复杂度与解密图像清晰度等各项评判指标仍是目前量子图像密码研究方向的重点。

基于混沌系统的量子图像加密算法具有密钥强敏感性和巨大的密钥空间，能够抵抗许多非法攻击[14,22,23]，提高图像密码方法的安全性与加解密效率。量子细胞神经网络作为混沌系统可以实时、并行地对信号进行处理，并被广泛应用于数据量大的图像处理当中。此外，相对于传统的细胞神经网络，量子细胞神经网络还具有低消耗、高集成的特点，因而更符合实际应用需求[16,23]。量子酉操作(量子逻辑门)具有可逆性，即在保证量子态不被破坏的情况下，量子逻辑门的输入、输出态可以进行相互转换，可用于提高解密图像的清晰度。为此，本文结合量子细胞神经网络和量子酉操作，提出一种新的量子灰度图像混沌加密方法，在确保量子图像加密算法安全的基础上，进一步优化解密图像清晰度及计算复杂度。此外，本方案中所涉及的图像处理操作包括量子细胞神经网络(混沌系统)均可由量子线路实现，表明本方案具有在量子设备上实现的前景。

2 理论基础

2.1 量子细胞神经网络的超混沌属性

混沌是非线性系统中普遍存在的现象。混沌系统[15,24]凭借不确定性、不可重复性和不可预测性被广泛应用于密码学中。超混沌系统属于高维度混沌模型，对于初始控制参数具有超敏感性。由多个量子细胞机构成的量子细胞神经网络属于一种超混沌系统[25,26]。具体来讲，量子细胞神经网络的第k个细胞机的动态特性表示为经网络的混沌属性，可以令w2为自变量，计算出该量子细胞神经网络的最大李雅普诺夫指数[28]。如图2所示，最大李雅普诺夫指数值均大于0，证明耦合2个细胞机的量子细胞神经网络模型系统便很容易产生超混沌现象。

图2 量子细胞神经网络的最大李雅普诺夫指数

2.2 新型量子图像表示方法

可见，相比于经典图像表示方法，该量子图像表示方式能指数级降低图像存储空间：对于同一个2n×2n大小的经典灰度图像，该量子图像表示方式所需量子比特数为8 +2n，而经典图像表示方法则需比特数8 ×2n×2n+n2。另外，相比于其他量子图像表示方法[30,31]，该量子图像表示方式可以平方级降低制备图像的时间复杂度，且能够完全正确地表示出经典图像[16]，量子线路如图3所示。

图 1 量子细胞神经网络中P 1, P 2, φ 1之间的轨迹曲线

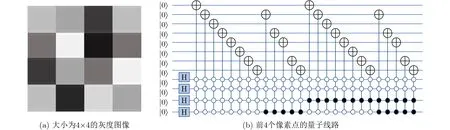
图3 新型量子图像表示量子线路图

2.3 量子Arnold变换

2.4 量子交换操作

在混淆像素位置之前，量子交换操作可以用于扩散图像像素值来增强密文图像的模糊性。量子交换操作Uxy的量子线路如图4所示，其应用到某一个像素值|f(x,y)〉上的表示为

图4 量子交换操作

3 量子灰度图像加密和解密方法

本节将着重介绍基于量子细胞神经网络的量子灰度图像加密和解密步骤。整体加解密过程如图5所示。图5所涉及的量子细胞神经网络超混沌同步技术可基于电路实现[36,37]，因此如何传输混沌信号(密钥参数)将不再赘述。值得注意的是，在3.1节和3.2节所涉及的处理对象均针对图像中的一个像素点。

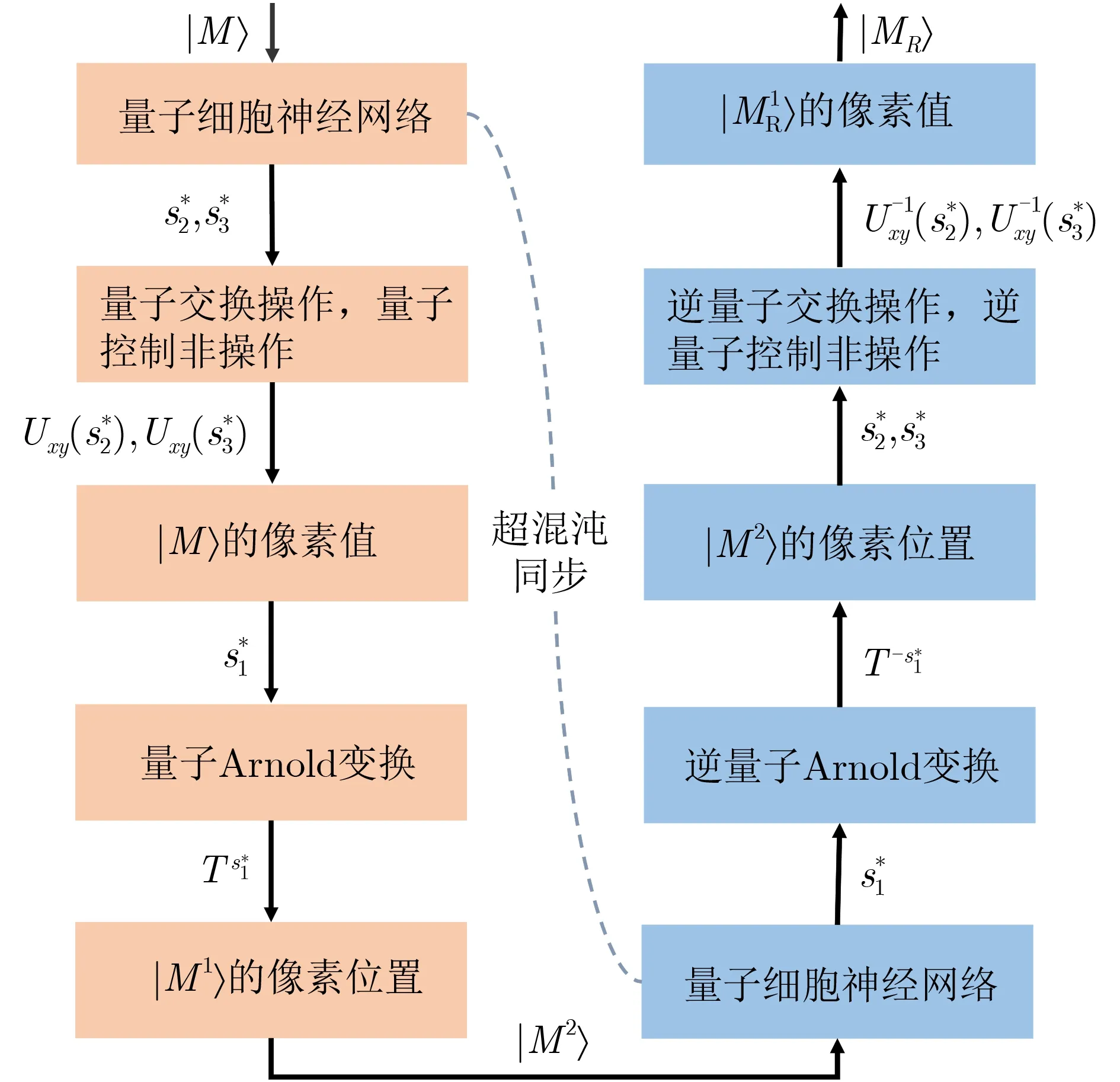
图5 图像加解密全过程

3.1 量子灰度图像加密步骤

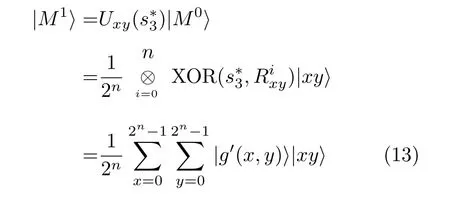
3.2 量子灰度图像解密步骤

b1b2w1w2P1(0)

(1)获取控制参数 , , , ，初始值 ,

4 仿真和理论分析

为了探求本方案的可行性及有效性，基于MATLAB平台，本文对方案加解密过程进行了仿真实验。所有的仿真实验均基于同一个量子细胞神经网络，并且给定的控制参数b1=b2=0.28,w1=0.7,w2=0.3 ， 初始值P1(0)=−0.348391961265269,P2(0)=3.18935060634640,φ1(0)=−0.0862955569903436,φ2(0)=5.76650621975721， 随机起始点N0=8，信号取值间隔N=10000。图6(a)、图6(b)分别展示了512×512大小的原始图像Woman和Pepper，图6(c)、图6(d)为Woman, Pepper加密后的图像。

图6 明文图像Woman, Pepper及相应密文图像

4.1 信息熵

信息熵(以下简称熵)是用于衡量一个图像(系统)混乱程度的重要指标[37]，其数学表达为

4.2 直方图分析

一个有效的图像密码算法应使不同密文图像具有相似的直方图。由图7可知，明文图像Woman和Pepper的直方图很不一样，但两者对应的密文图像直方图几乎一致，证明本方案具有有效性，能够较好地抵抗直方图攻击。

图7 明文图像Woman, Pepper及相应密文图像的直方图

表1 明文图像及相应密文图像的熵

其中，xi和yi为邻接像素。表2展示了明文图像及相应密文图像在水平、垂直、对角3个方向的相关性，从中可以看出，密文图像邻接像素相关性无论在哪个方向均接近于0。从图8可以看出，明文图像中邻接像素联系均很强-呈直线状，但密文图像中邻接像素联系均很弱-呈平铺状，证明本加密算法可强有力地混淆明文图像以很好地抵抗统计攻击。

图8 图像加密前后邻接像素的联系

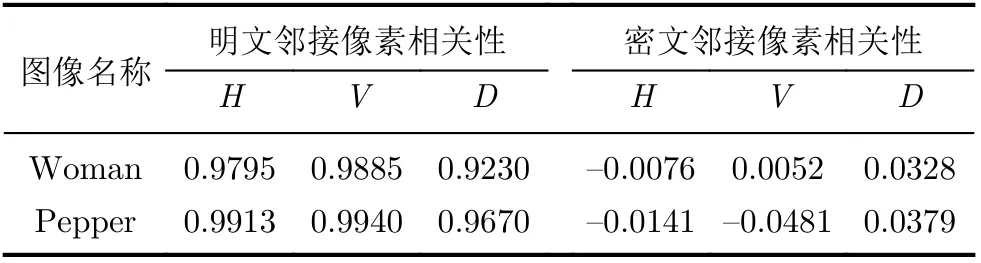
表2 明文图像及相应密文图像在水平、垂直、对角方向的相关性

4.4 密钥空间

对于图像加密算法来说，密钥空间需达到2100数量级才能较好地抵抗暴力攻击[38]。本方案中，密钥由b1,b2,w1,w2,P1(0),P2(0),φ1(0),φ2(0),N0,N构成。设非线性混沌系统中参数的有效精度为 1 0−14，结合本文中给出的实验数据，本图像算法的密钥空间可达到 10120≫2100。因此本方案具有巨大的密钥空间可以抵抗经典计算机甚至量子计算机带来的暴力攻击及唯密文攻击。

4.5 计算复杂度

4.6 密钥敏感性分析

密钥出现极其微小的改变从而导致获得非理想的解密图像，这种现象称为强密钥敏感性。密钥敏感性可由直观的解密图像变化来评估。以明文图像Lena为例，从图9可以看出，即使密钥有极小的偏移，也不能解密出正确的图像，说明本方案具有较强的密钥敏感性，能够抵抗密钥攻击，证明了本方案的安全性。

图9 不同密钥情况下解密出的Lena图像

5 结论

基于量子Arnold变换与量子逻辑操作，本文以确保图像算法安全为基础，利用超混沌系统量子细胞神经网络增强加密过程中的不确定性和不可预测性，提出一种量子灰度图像混沌密码方法。其具有以下优势：(1)为进一步模糊明文图像，对明文图像行像素值和列像素值均作了扩散处理。根据理论分析，本方案具有高安全性可以抵抗许多非法攻击，如熵攻击、统计攻击；(2)为进一步降低图像加密过程的计算复杂度，引入迭代量子Arnold变换、量子交换及量子控制非操作，将算法计算复杂度降为O(n)，为至今所提出的量子灰度图像密码方案中的较优值；(3)为进一步提高解密图像质量，图像加密操作全由可逆的量子逻辑门实现，在密钥完全正确的情况下，本文方案能以较高保真度(100 dB)恢复出明文图像。