基于改进离散蝙蝠算法的无线Mesh网络部分重叠信道分配

叶 方 孙 雪 李一兵

(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

(先进船舶通信与信息技术工业和信息化部重点实验室 哈尔滨 150001)

1 引言

无线Mesh网络(Wireless Mesh Networks, WMN)因其多跳、自组织、非视距传输等优点，以及在覆盖范围、成本控制、组网速度等方面的优良表现，广泛应用于灾后网络重建等应急通信场景[1,2]。然而随着网络规模的增大，网络拓扑复杂化，WMN中信道干扰的情况也会越来越严重，多射频多信道(Multi-Radio Multi-Channel, MRMC)技术是一种能够显著降低共信道干扰，提高网络性能的方案[3]，但也随之带来了频谱利用和链路冲突等问题。因传输范围远而被广泛使用的IEEE 802.11b/g标准中相邻信道的频谱部分重叠，正交信道只有3条[4]，因此如何在一定限制条件下合理高效地对有限频谱资源进行分配，在降低干扰的同时保持网络稳定是应急通信网络面临的重要挑战。

针对WMN信道分配中频谱资源有限的问题，Mishra等人[5]提出了干扰因子的概念来描述IEEE 802.11b/g标准中信道的重叠程度，研究表明利用部分重叠信道 (Partially Overlapped Channels, POCs)能够在一定程度上提高信道频谱资源复用。Bokhari等人[6]提出了一种利用部分重叠信道实现干扰感知的信道分配方法，证明了所提算法能够显著降低由MRMC引起的网络干扰，相比于仅使用正交信道网络性能提高了37.3%。文献[7]在保证网络连通性的同时使干扰最小化，证明了适当使用重叠信道的信道分配可以提高网络吞吐量，尤其是在密集拓扑网络中，然而该方法以牺牲时间复杂度为代价寻求性能的提升，需要设计更高效的算法降低复杂度。

针对节点增加时引起的网络复杂化问题，许多研究将信道分配过程转化为带有约束条件的线性规划模型，利用群智能算法求最优解[8]。文献[9]采用禁忌搜索算法进行信道分配，避免在搜索过程中出现已经访问过的解决方案，能够一定程度上提高局部搜索能力，但是禁忌搜索的结果完全依赖于初始解和邻域的映射关系，全局搜索能力弱。文献[10]针对应急通信需求提出了基于权重的粒子群优化算法，构建有序链路矩阵和链路邻接矩阵解决重要链路的网络拥塞问题，精确地将不同链路在网络中的重要性进行区别和记录，但是该方法没有考虑MRMC中的接口约束条件和频谱资源问题，同时粒子群算法收敛速度慢且易陷入局部最优。文献[11]引入“载波侦听多路访问(Carrier Sense Multiple Access,CSMA)感知”的共享链路容量模型解决链路容量计算和流量感知的问题，采用混合整数规划来优化信道分配过程[11]。但是该算法只实现了3～5个正交信道的无冲突分配，且当节点增多时混合整数规划求解困难。文献[12]通过贪婪启发式算法进行以最小化邻信道干扰为目标的信道分配，但该方法以从0～1变化的公平性指数来衡量流量变化，没有将流量对网络性能的影响考虑在目标优化函数内。文献[13]基于时隙模型以节点间最大流量为目标进行全局链路调度来提高网络容量，但没有考虑干扰对吞吐量的影响且缺少公平性约束。

以上WMN信道分配方案大多存在着频谱资源利用不充分，没有考虑实际工作中可能存在的流量汇聚情况和接口约束条件的问题。针对上述问题，本文综合考虑邻接链路数量和信道干扰建立以最小化链路加权干扰为目标的优化函数，将静态信道分配过程转化为带有约束条件的线性规划模型，使算法在节点数目增加时仍能保证网络的稳定性和连通性。针对节点增加时网络拓扑复杂化导致信道分配效率低的问题，考虑蝙蝠算法在资源调度领域展现的优秀搜索能力[14]，提出改进离散蝙蝠算法(Improved Discrete Bat Algorithm, IDBA)求解最优信道分配方案，在标准蝙蝠算法的基础上，将种群位置和速度的更新离散化，参考樽海鞘群算法中的链式行为提高局部搜索能力，引入动态惯性权重有效平衡算法的全局搜索和局部开发能力从而得到更快的收敛速度，大幅度减少全局链路干扰，提高网络吞吐量。

2 系统模型及问题描述

2.1 网络模型

在如图1(a)所示的应急场景中，各Mesh路由器自主构建多跳自组织的网络系统拓扑，为应急现场的终端设备提供通信服务并完成面向指挥中心的信息回传等任务。

采用如图1(b)所示的WMN骨干型结构，在IEEE 802.11b标准基础上用一个无向图G(V,E)来表示WMN。其中，V是网络节点的集合，代表Mesh路由器；E是网络节点形成的链路集合。Mesh路由器配备K(K ≥2)个无线接口，可用部分重叠信道集为C，其中信道个数为cn。C(v)表 示节点v分配的信道集合，集合中元素的个数为|C(v)|。

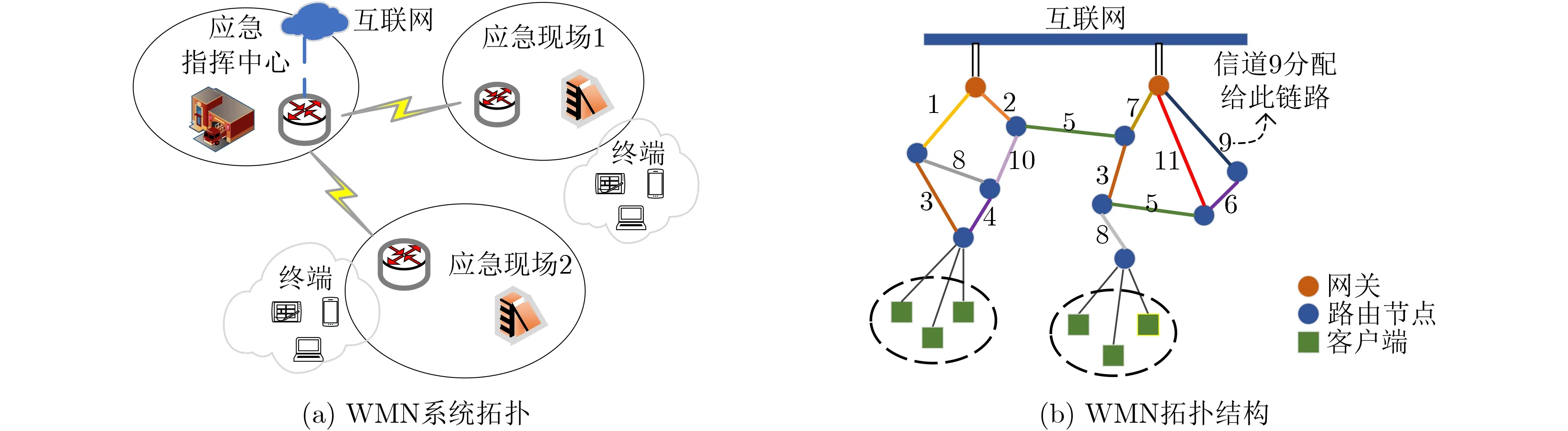
图1 WMN网络拓扑

考虑所有Mesh路由器的无线接口发射功率和传输范围相同；信道分配与路由独立跨层优化，在信道分配之前已经设计好路由路径。设传输范围为Rt， 即一跳的传输距离。对于网络中的节点i,j∈V，定义它们之间的距离为dij，g(eij)表示节点间的链路存在情况，当dij ≤Rt时 ，节点i和 节点j之间的链路eij存在；当dij>Rt时，两节点之间不存在链路，即

网络中的每个节点在某个时刻进行数据通信时，同一时刻1个射频接口或者只被分配了1个信道，或者没有被分配信道，因此节点上被分配的信道数不可能超过节点自身配备的无线接口数[15]，即满足式(4)约束条件

2.2 干扰模型

采用基于双径传播的协议干扰模型[16]进行干扰建模，由于正交信道(Orthogonal Channels, OCs)只受同信道干扰影响，节点i和 节点j之间的干扰范围RI(0)为

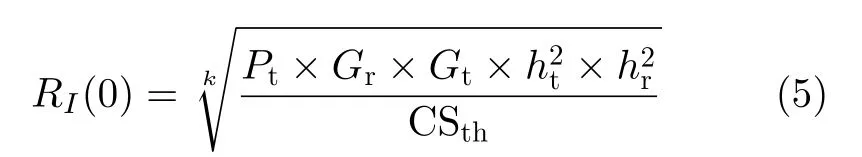
其中，Pt是 节点的发射功率；Gr是接收节点的天线增益； CSth是载波感知门限；k是路径损耗因子；Gt是发射节点的天线增益；hr是接收天线的高度；ht是发射天线的高度。

而POCs的干扰范围与信道重叠度有关，od(x,y)表示两信道cx和cy间隔为τ=|x −y|时的信道重叠度，具体如表1所示[17]。

表1 信道重叠度

使用POCs的干扰范围为

为了更清楚地反映网络整体的干扰情况，本文用冲突图Gc(Vc,Ec)来描述链路间干扰[18]。定义图2(b)中的冲突图顶点为图2(a)中拓扑图两顶点之间形成的链路，即Vc={eij|eij ∈E}。 若图2(a)中链路lab处于链路lac的 干扰范围内，则图2(b)中的lab和lac间有一条连接线，表示一条干扰链路。

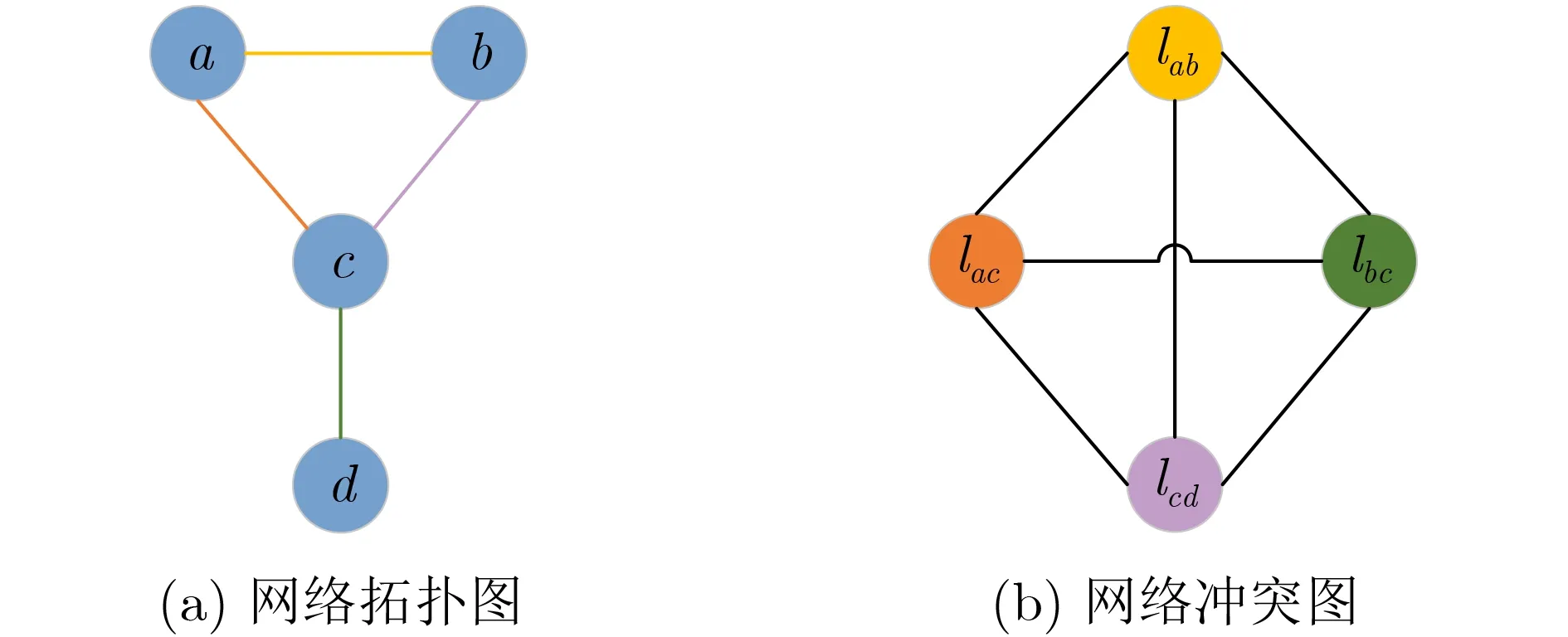
图2 拓扑图与冲突图对应关系

a为所求链路eij的编号，b为与a之间存在干扰的链路的编号，链路eij受到的总干扰为

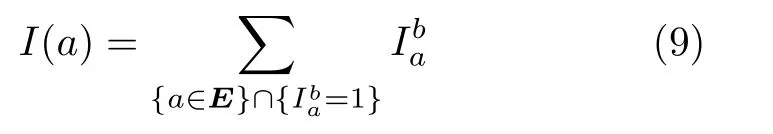
2.3 问题描述

在实际网络环境中，相邻链路越多的链路表现为流量越多，易形成瓶颈链路，所以在信道分配时需要对相邻链路多的链路着重考虑，以提高应急通信网络在流量汇聚情况下的稳定性。定义邻接链路权重ωij为所求链路eij的相邻链路数量在全部链路中的占比，Lij为所求链路eij的相邻链路数量总和，L为网络中的全部链路数，即

综合考虑网络的邻接链路权重和链路干扰，网络总加权干扰为

3 基于改进离散蝙蝠算法的部分重叠信道分配

蝙蝠算法通过模拟自然界中蝙蝠利用超声波感知猎物并捕获的能力进行最优化目标求解[19]。标准蝙蝠算法[20]求解的都是连续型问题，为了使其能够处理WMN信道分配问题，需将其进行离散化并做相应改进。

3.1 改进的蝙蝠运动方式

表2 蝙蝠位置编码示例

3.2 改进的局部搜索方式

3.3 信道分配算法

在建立网络模型和干扰模型的基础上，算法的适应度函数为网络的总链路加权干扰，即

4 实验结果及分析

4.1 仿真环境与参数设置

在Matlab环境下对本文所提基于IDBA的WMN部分重叠信道分配方法进行仿真，并与文献[10]中基于离散粒子群优化 (Discrete Particle Swarm Optimization, DPSO)算法的信道分配方法、文献[22]中基于布谷鸟搜索算法 (Cuckoo Search Algorithm, CSA)的信道分配方法和文献[23]中基于离散鸽群优化 (Binary Pigeon-Inspired Optimization, BPIO)算法的信道分配方法进行对比分析。所用计算机的配置参数为：AMD Ryzen 9 3900X 12-Core Processor；3.8 GHz主频；32 GB RAM；Windows10操作系统。具体参数设置如表4所示。

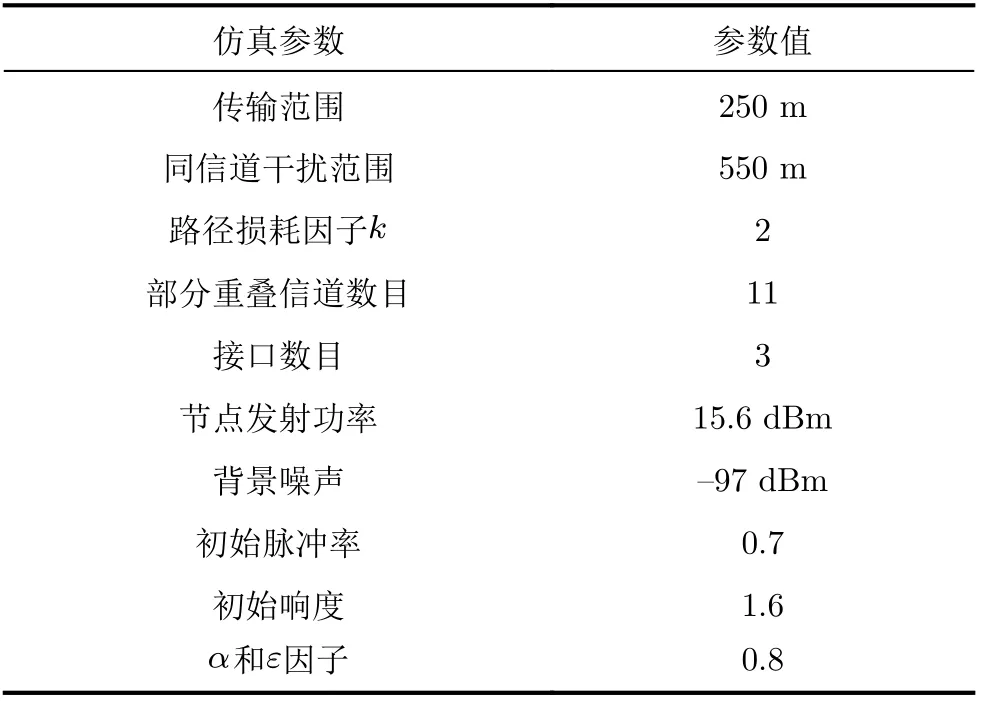
表4 仿真参数设置表

4.2 模型建立

为了使算法更加具有一般性同时避免均匀网格类拓扑产生不必要的通信链路开销，仿真实验中在一个1000 m×1000 m的2维空间内采用Salama模型随机部署25个Mesh节点，部署后各节点固定不动。同时实验采用K-means聚类算法使网络节点均匀分布避免随机部署时节点过于集中或分散，从而覆盖更大的应急通信范围。生成如图3所示的网络拓扑图，该图反映了当两节点间距离小于传输距离时，两节点间存在链路，即两个节点之间存在一条边。

图3 网络拓扑图

设置相同网络区域内的网络节点数分别为20和40，根据建立的干扰模型得到了图4(a)稀疏节点和图4(b)密集节点下的网络冲突图。图4反映了链路间的干扰情况，标号代表链路编号，可见当节点数目增多时链路间的干扰十分严重，因此进行合理的信道分配以减少网络干扰是十分必要的。

图4 网络冲突图

4.3 算法复杂度分析与对比

表3 信道分配过程

图5描述了在不同节点数量下各算法达到收敛时的平均迭代次数变化情况，设置相同网络区域内节点数目分别为20, 25, 30, 35, 40, 45, 50，其他网络环境相同。可见DPSO算法虽然时间复杂度低但是其收敛时间缓慢，甚至在迭代次数即将达到100时才开始收敛，搜索效率低；CSA和BPIO算法不稳定，在搜索过程中易陷入局部最优，收敛时间较长；而IDBA在不同网络规模下，其收敛时的平均迭代次数均为最低，因此具有较高的搜索效率。

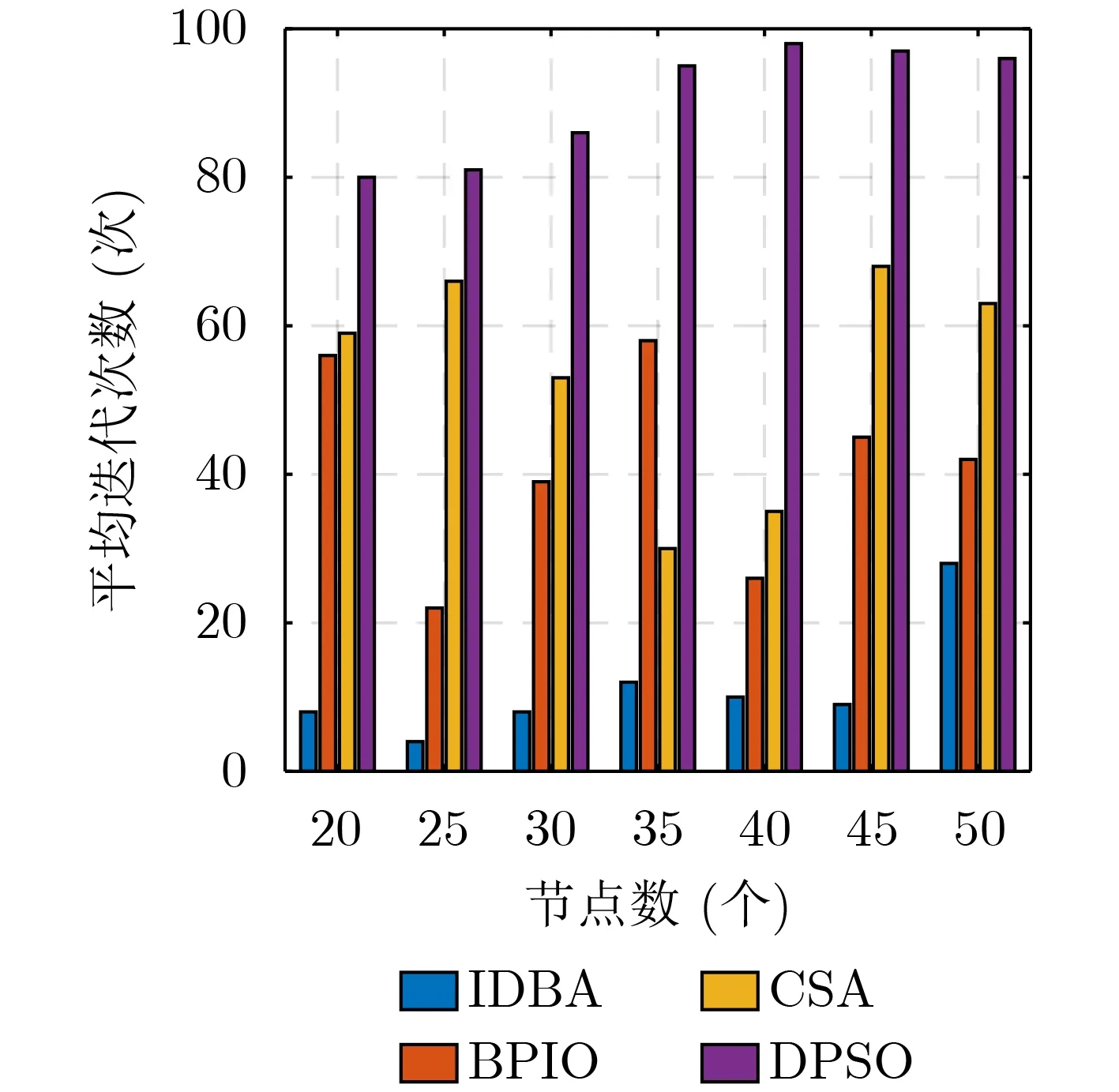
图5 不同节点数下收敛时间对比

表5通过描述各算法在不同网络规模下仿真的运行时间来进一步反映算法的总计算时间，仿真环境相同。可见DPSO耗时最少，这是通过牺牲算法的搜索性能换来的；BPIO时间复杂度最高，因此算法总计算时间最长，尤其是在大规模网络下性能不佳。IDBA和CSA信道分配方法的数学估计时间复杂度相同，但是CSA通过随机游走进行局部搜索，容易陷入局部最优，因此仿真消耗的总时间较长。综上所述，IDBA能够在不同网络规模下保持较高搜索效率，同时具有较低的时间复杂度。

表5 不同算法总耗时对比(s)

4.4 算法性能分析与对比

图6通过描述各算法随着迭代次数的增加适应度值(链路加权干扰值)的收敛情况来反映算法的优化效率和优化程度，所有算法均采用相同的最大迭代数100次，种群数量50和网络节点数25。由图6分析可知，随着迭代次数的增加，各算法链路干扰逐渐降低直至收敛。在收敛速度上进一步证明了IDBA在迭代10次左右时其适应度值就可以收敛到最优；DPSO算法在信道分配中搜索能力表现不佳，收敛速度十分缓慢；CSA和BPIO算法搜索速度相对较快但是易陷入局部最优。在搜索能力上，IDBA表现最好，收敛时的网络干扰最低，因为蝙蝠根据响度和频率的变化逐渐向最优目标靠近保证了其优秀的全局搜索能力，同时引入了樽海鞘群的链式行为提高其局部开发能力，动态惯性系数有效平衡了全局搜索和局部开发之间的关系。

图6 不同算法适应度收敛曲线对比

图7描述了随着网络节点数目的增加网络干扰的变化情况，设置网络环境中节点数目分别为20,25, 30, 35, 40, 45, 50，其他网络环境相同。随着网络节点数目的增加，在迭代相同次数后得到的链路加权干扰值增加，DPSO算法的链路干扰十分严重，尤其在节点密集的情况下性能不佳；CSA,BPIO和IDBA在节点数小于30的情况下性能相差不大，但在节点密集时IDBA算法链路干扰值最小且随着网络规模的增大链路干扰值增长幅度最小。

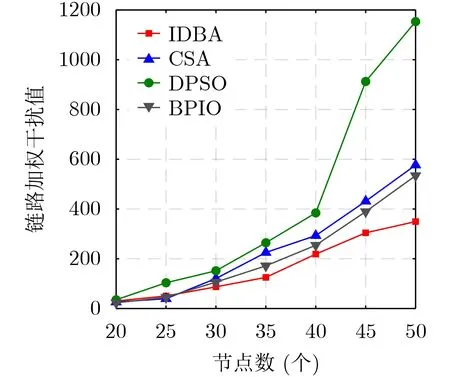
图7 不同节点数下全局干扰值对比

图8描述了随着网络节点数目的增加网络吞吐量的变化情况，设置网络环境中节点数目分别为20, 25, 30, 35, 40, 45, 50，其他网络环境相同。各算法迭代相同次数后根据链路分配的最优信道计算网络吞吐量，在节点数目不超过35时，随着节点数目的增加，各算法的网络吞吐量都增加，IDBA算法的性能最好，吞吐量最大，优于其他3种算法；当节点数目大于35时，DPSO算法由于链路干扰急剧增加而使网络变得不稳定，网络吞吐量下降并产生波动；在网络规模达到40个节点后IDBA和CSA吞吐量有明显下降；IDBA算法的吞吐量在小幅度增长后趋于一个稳定值，且其吞吐量总是高于其他3种算法，由于此时网络可兼容量达到峰值，故网络吞吐量不再有显著的提升，说明IDBA在节点密集场景下仍能较好地保持网络稳定性。

图8 不同节点数下网络吞吐量对比

5 结束语

本文讨论了应急通信背景下WMN的集中式静态信道分配问题，利用部分重叠信道提高频谱利用率和网络性能。针对流量汇聚场景下存在的瓶颈链路问题和网络干扰情况，建立以最小化链路加权干扰为目标的信道分配优化模型，采用改进的离散蝙蝠算法进行目标求解，将蝙蝠的运动方式离散化并引入樽海鞘群的链式行为提高局部搜索能力，通过迭代得到最优信道分配方案。实验表明了本方案能够有效降低网络干扰，提高网络吞吐量，能够应用在流量密集的应急通信场景下为客户端提供稳定的通信服务。