分层一点法应用研究——以延安气田上古生界M井区为例

张 力 和向楠 穆景福 徐云林

（陕西延长石油（集团）有限责任公司研究院，陕西 西安 710075）

0 引言

对气井产能的评价，传统的回压试井法、等时试井法以及修正等时试井法总体耗时长、测试条件高、投入经济成本大，对气田大多数气井不易实现，因此国内外研究者提出通过对系统试井资料分析处理得到适合本气田的一点法公式来评价气井产能[1]。如陈元千[2]根据四川16个气田的16口气井的多点稳定流试井资料，建立了适应于中、高渗的一点法公式。景艳等人[3]根据普光气田4口井测试资料修正了α值，得到了普光气田产能预测的一点法公式。以上气田获取的一点法公式对开发层系单一、均质、高渗的气田的适用性较好，而对发育多套层系的单采或多层合采井、非均质性强、低渗致密气田来说，单一的一点法公式代表性、针对性还有待加强研究，按层位精细建立一点法公式也未见相关研究分析。

因此，考虑延安气田上古生界各层的物性特征及地层压力差异，开采模式有单层与多层合采，且每口井的系数α值也不同，为了更客观地评价气井产能，该文提出了根据层位来处理修正等时试井资料，建立各层位的产能一点法公式。

1 分层一点法公式的建立

1.1 基本原理

在有边界限制的致密砂岩井区，随着天然气不断被采出，压力与产量的关系符合二项式产能方程[4]的形式，如公式（1）所示。

式中：pR为储层原始地层压力，MPa；pwf为井底流动压力，MPa；A、B为产能方程系数；qg为气井井口稳定产量，104m3/d。

当气井的井底流压pwf=0.101MPa时，理论上气井的最大产能即为气井的无阻流量qAOF，p2R-0.1012≈p2R，所以公式（1）可以表示为公式（2）。

式中：qAOF为气井无阻流量，104m3/d。

令α如公式（3）所示。

式中：α为系数，无因次。

通过公式（1）和公式（2）相除，并解关于q的方程，得到无阻流量的表达式如公式（4）所示。

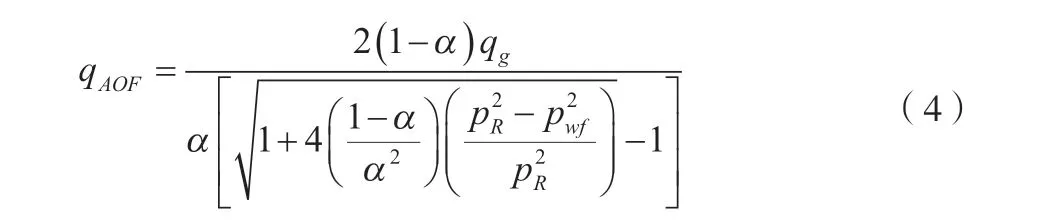
由公式（4）可知，当测得一个稳定产气量qg条件下对应的井底流压pwf，并得知测试前初始条件的地层压力pR以及系数α，就可求得该井的绝对无阻流量，此方法即为获取气井无阻流量的一点法。由于一点法测试可快速获取qg、pwf、pR计算参数，因此获取恰当的系数α值是快速获取气井无阻流量的关键因素。

根据公式（1）和公式（3）可知，每口气井的二项式产能方程系数A、B值及无阻流量qAOF均不同，导致各井的系数α也不同。一个气田含有多个气层时，每个层位的地质特征不同，系数α也有差异[5-8]。延安气田M井区属于上古生界低渗致密砂岩储层，主力气层为本溪、山23、山1、盒8[9]。从M井区历年修正等时试井资料得知，系数α值各层均有差异，为了更精细地评价延安气田M井区的气井产能，有必要建立符合各层地质特征及动态特征的一点法产能公式。

1.2 处理修正试井资料确定系数α值

以层为单位对修正等时试井资料进行分析，有效渗透率K及有效厚度取试井解释值，根据公式（3）计算系数α值，各层地层系数Kh与系数α数据见表（1）～表（5）。各层的系数α值取各层α值的平均值作为该层系数α值的计算值。其中，本溪层系数α值在0.5057～0.8806，平均值为0.6942，地层系数Kh在3.9md·m～36.72md·m。

山2层系数α值在0.4200～0.9762，平均值为0.7132，地层系数Kh在4.55md·m～177.46md·m。

山1层系数α值在0.7837～0.8665，平均值为0.8252，地层系数Kh在2.56md·m～10.35md·m。

盒8层系数α值在0.7301～0.8869，平均值为0.8194，地层系数Kh在3.66md·m～9.40md·m。

多层合采层系数α值在0.6980～0.8866，平均值为0.7814，地层系数Kh在1.37md·m～14.62md·m。

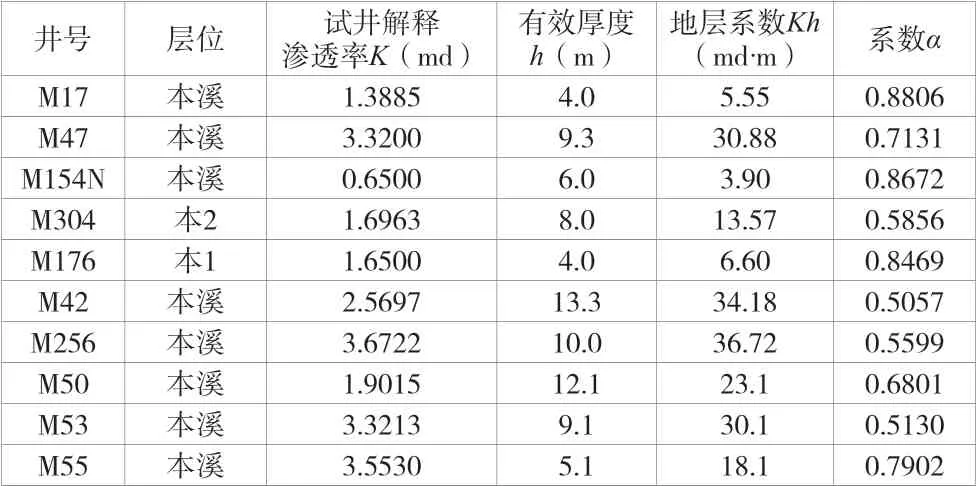
表1 本溪层各井地层地层系数与系数α值

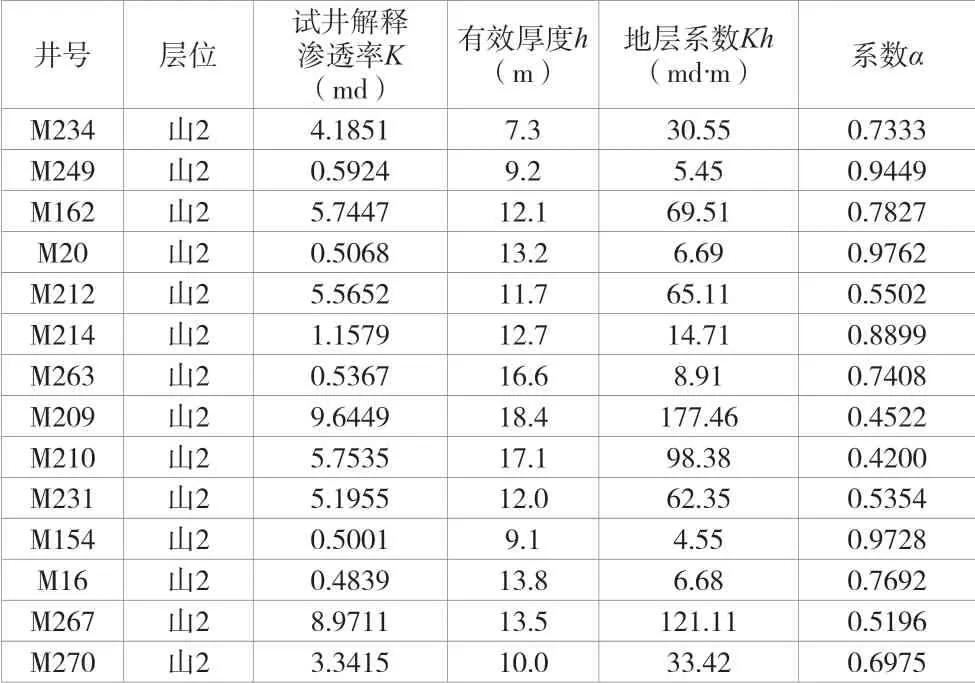
表2 山2层各井地层地层系数与系数α值

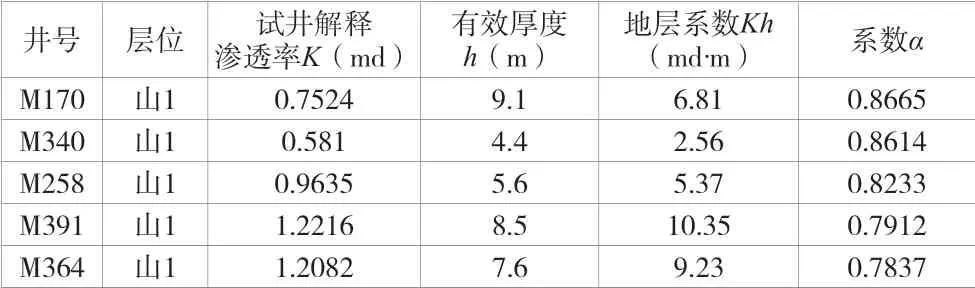
表3 山1层各井地层地层系数与系数α值

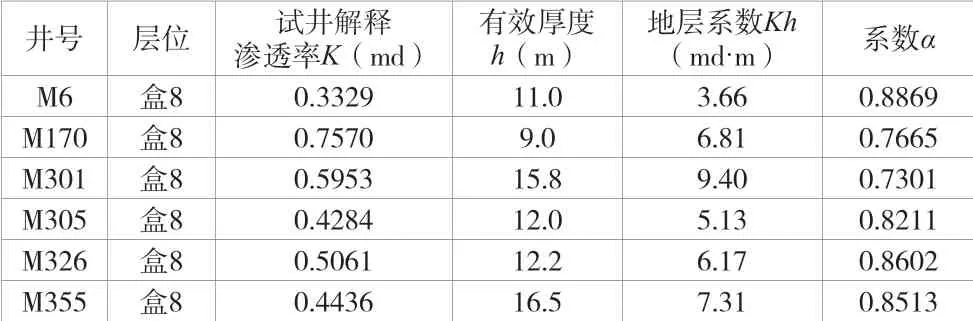
表4 盒8层各井地层地层系数与系数α值

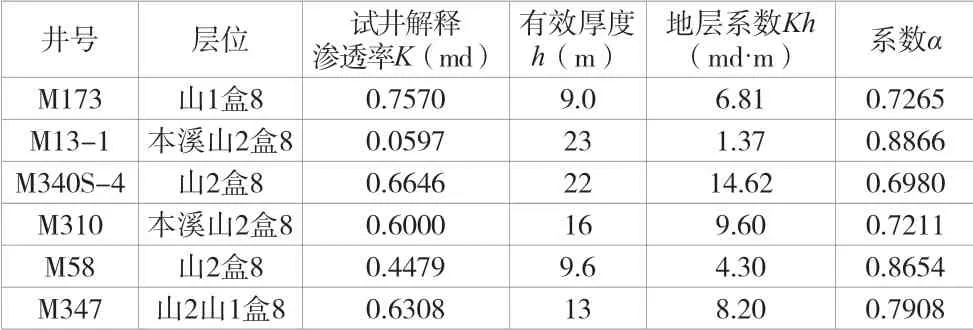
表5 多层合采各井地层地层系数与系数α值

1.3 地层系数法确定系数α值

通过对地层系数Kh与系数α值进行回归分析，发现各层的地层系数Kh与系数α值存在一定的关系（如图1～图5所示）。回归得到各层地层系数Kh与系数α的关系式如公式（5）所示。

图1 本溪层各井系数α值与地层系数Kh的关系

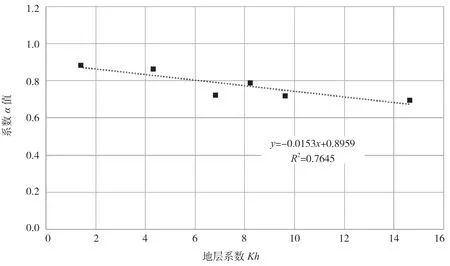
图5 合采层各井系数α值与地层系数Kh的关系

其中，本溪层地层系数Kh与系数α值满足线性关系，斜率为-0.0097。山2层地层系数Kh与系数α满足对数关系，相关性较好。山1层地层系数Kh与系数α值满足线性关系，斜率为-0.0098。盒8层地层系数Kh与系数α值满足线性关系，斜率为-0.0239。合采层地层系数Kh与系数α值满足线性关系，斜率为-0.0153。

1.4 分层一点法公式的建立

根据第1.2节中确定的各层位系数α的计算值，将其代入公式（4），可得延安气田上古生界各层位的一点法产能公式，其中，山2层如公式（6）所示。

本溪层一点法公式如公式（7）所示。

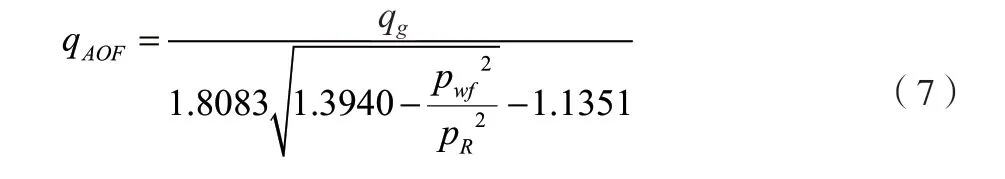
盒8层一点法公式如公式（8）所示。

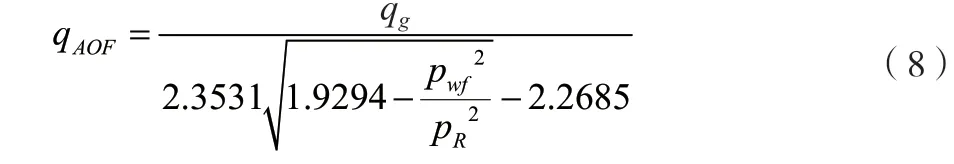
山1层一点法公式如公式（9）所示。

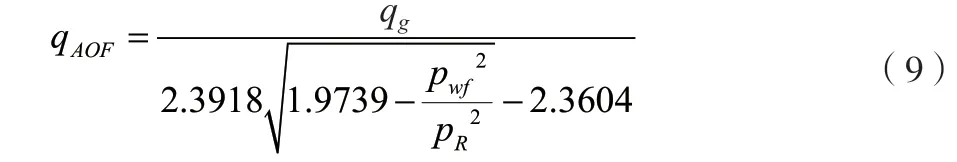
合采层一点法公式如公式（10）所示。

2 应用效果分析

以延安气田M井区4口不同层位试气井为例，该4口井分别进行了修正等时试井及压力恢复试井，应用该文建立的各层位一点法产能公式及各层根据地层系数Kh求取系数α值后计算各井无阻流量，并与修正等时试井计算的无阻流量对比，以验证该文所建公式的合理性。以下为4口井压力恢复试井解释的相关参数（见表6）。

将表6中各井的地层压力pR、井底流压pwf及稳定点的产气量qg按层位分别代入公式（6）～公式（10），可以计算出各井的初始无阻流量qAOF，并以修正等时试井所得的无阻流量作为标准，其他各公式计算的无阻流量与之对比并进行误差分析，计算结果分别如表7和图6所示。

图6 各公式计算无阻流量与修正等时试井无阻流量对比

表6 4口井压力恢复试井相关参数

表7 各公式计算无阻流量与修正等时试井计算无阻流量对比及误差分析

延安气田原经验公式计算的无阻流量与修正等时试井所得无阻流量误差在5.36%～20.08%，平均误差为11.40%，二者计算结果有一定差异，其中用原经验公式计算本溪层Y230井的无阻流量时误差最大，达到20.08%（如图7所示）。

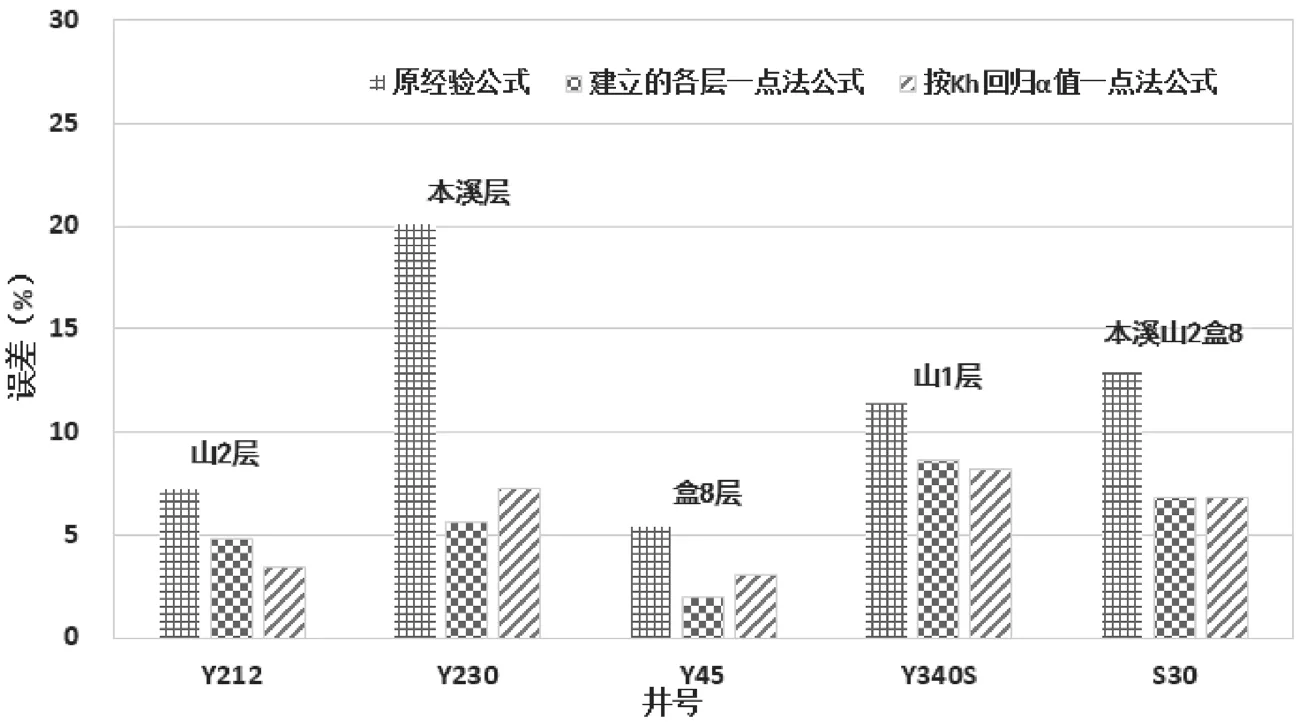
图7 各公式计算无阻流量与修正等时试井无阻流量对比误差分析

采用所建立的各层位一点法公式计算的无阻流量与修正等时试井所得无阻流量误差在1.97%～8.68%，平均误差为5.57%，两种计算结果总体比较接近。

采用各层地层系数Kh回归α值后代入一点法通式计算的无阻流量与修正等时试井所得无阻流量误差在3.07%～8.22%，平均误差为5.76%，两种方法计算结果也比较接近。

综上分析，与规范的修正等时试井评价气井产能结果相比，气田采用原经验公式评价各层气井产能时误差普遍较大，而采用该文所建立的延安气田M区各层位一点法公式与由各层地层系数Kh回归α值后代入一点法通式两种方法计算所得的无阻流量误差更小，这两种方法的平均误差在5.5%左右。因此，采用该文所建立的两种方法进行延安气田气井初期产能评价，评价结果更准确。因此，该文建立的两种方法对延安气田初期气井产能的评价具有重要意义。

图3 山1层各井系数α值与地层系数Kh的关系

图4 盒8层各井系数α值与地层系数Kh的关系

3 结论

该文根据层位处理修正等时试井资料分别获取各层的α值，据此建立了延安气田上古生界各层位产能一点法公式，其计算结果较原经验公式误差更小。对气田其他地质特征类似的区块，可根据该文对应层位的一点法公式进行气井初期产能评价。

掌握地层系数中的渗透率K及有效厚度h后，可通过该文建立的地层系数Kh与系数α的关系式来快速获取一口气井的系数α值，并根据对应层位的一点法公式计算气井无阻流量。