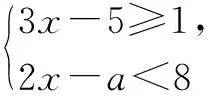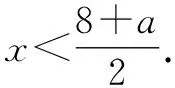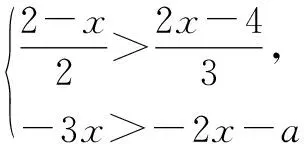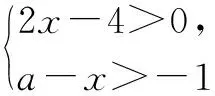含参一元一次不等式(组)问题求解策略
⦿山东省广饶县英才中学 徐树光
1 引言
若一个不等式中除了含有未知数以外,还含有其他字母,则称这个不等式为含参数的不等式.一般解题策略是先把不等式化为一边是未知数,另一边是数字或含参数的表达式,再根据题目的其他条件对表达式的正负情况讨论解答.下面以2020年中考题为例探求含参一元一次不等式(组)问题的求解策略[1].
2 直接使用口诀
由两个一元一次不等式构成的不等式组,共有四种情况.已知a 利用这个口诀,有时可以快速解题. 因此应填:a≥1. 点评:用口诀解“不等式组有解或无解”问题比较方便,但需要注意解集中等号的取舍,这对初学不等式的学生是一个难点.对此类问题还可以作以下变式: 由于参数的存在,各不等式解集端点的值大小关系待定,用分类讨论作答,可看出不同情况下的解集,符合题意的范围即为要求的答案. 当a=2时,原不等式组的解集是x>1; 当a<2时,原不等式组的解集是x>1. 所以a的取值范围是a≤2. 点评:分类讨论将所求问题细化,多次使用口诀解答,找到满足题意的参数的范围;同时,也排除了不合题意的参数范围. 不等式中的参数问题本质是在运动与变化中寻找满足题意的范围,有时临界点较多,利用数形结合可以使问题直观形象,降低思维难度,尤其对等号的取舍有重要的支撑作用. 例3(2020年天水改编)若关于x的不等式3x+a<2的最大整数解为2,则a的取值范围是. 图1 图2 图3 因此,a的取值范围是-7≤a<-4. 点评:数轴是数形结合的有力工具,利用数轴将不等式的解集直观表示出来,可以快速准确地建立含参不等式,对难于抉择的端点也可一目了然. 当一个问题有多种可能性,或不易直接解答,可从问题的反面分析研究,即利用补集思想解决. A.m>-1 B.m≥-1 C.m≤-1 D.m<-1 解析:解不等式组,得x>1,且x≤-m.考虑从反面出发,求原不等式组无解时,a的取值范围.由前面的口诀,知-m≤1,即m≥-1时,原不等式组无解,即不等式有解的范围是m<-1.故选:D. 点评:正难则反是一种重要的思维方式,巧妙运用这个策略,适当转变思路,尝试逆向思维对题目进行分析,能够降低思维难度,减少运算量. 不等式中有关取值范围的问题,对端点的取舍容易出错,因此对于一些选择题,只需把端点处理好,采取端点验证法,可以减少运算量. A.0≤a≤2 B.0≤a<2 C.0 解:从选项中发现,解决本题的关键在于0和2是否可取. 由3x-5≥1,得x≥2. 当a=0时,不等式组的解集是2≤x<4,有两个整数解,不合题意,所以舍去a=0.排除A,B选项. 当a=2时,不等式组的解集为2≤x<5,有三个整数解,符合题意,所以a=2可取. 因此应选:C. 点评:对于一个数学问题,能直接解答固然很好,而从不同角度思考问题,特别在考试的有限时间内快速得出答案,既可节省时间,又可提高正确率,是非常有益可取的做法. 以上含参不等式的五种求解方法,要因题而异,根据题设灵活选用,尤其是等号的处理,要正确理解.下面让我们运用这几种方法大显身手吧! A.a≥2 B.a<-2 C.a>2 D.a≤2 解析:解不等式组得x<2且x 解析:解不等式组,得x>2且x 解析:解不等式组,得x<4-a且x>-1.则不等式组有解时,满足-1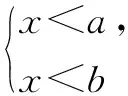
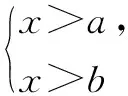
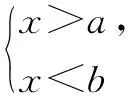
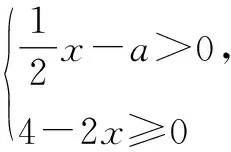
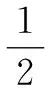
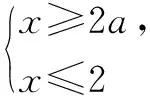
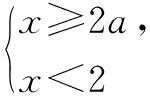
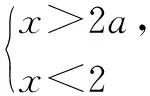
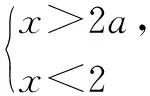
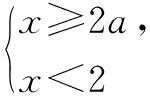
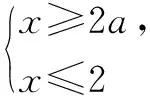
3 分类讨论
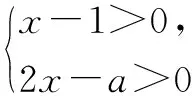
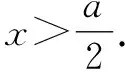
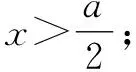
4 数形结合
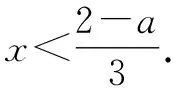
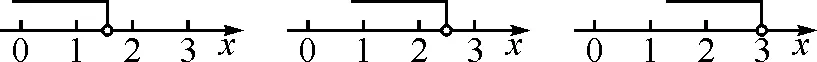
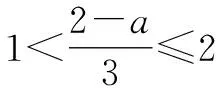
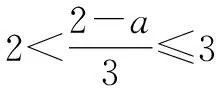
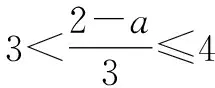
5 补集思想
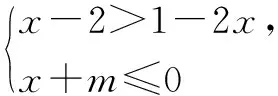
6 端点验证