探究方根本质 寻求问题解答

⦿常州市武进区湖塘实验中学 蒋 飞

1 用定义求方根

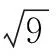
分析：由平方根的定义知道正数的平方根是一对相反数，它们的平方等于被开方数，其中正的平方根是它的算术平方根；负数没有平方根，也不存在算术平方根；任何一个数都有立方根，其符号与原数的符号相同．

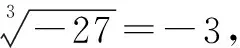
点评：正确理解平方根、立方根、算术平方根的定义是解题的基础，依据乘方与开方互为逆运算是解题的重要策略．

2 用方根定义解方程

例2解下列方程：

分析：把(5x-3)2，(x-1)3均看成an的形式，再根据乘方与开方互为逆运算求解．

(2)原方程可化为(x-1)3=343.因为73=343，所以x-1=7，即x=8 ．

点评：解此类方程的实质还是求一个数的方根的运算，其解题过程是由繁到简的转化过程，即逐步化为xn=a的形式．

3 用方根性质求值

例3已知3x+2和2x-12是m的平方根，求m的值．

分析：一个正数有两个平方根，且它们互为相反数.互为相反数的两个数的和为0 ．

解：根据题意，分两种情况.

(1)因为3x+2和2x-12都是m的平方根，所以

(3x+2)与(2x-12)互为相反数.

所以(3x+2)+ (2x-12)=0.

解得x=2，并代入m=(3x+2)2中，得m=64；

(2)当3x+2=2x-12时，x=-14，此时

m=(3x+2)2=(-40)2=1 600 ．

综上可得m的值为64或1 600 ．

点评：习惯上我们意识到一个正数有两个不同的平方根，但此处用代数式表示的两个数并非一定不相等，此处容易忽略3x+2与2x-12相等的情形．

4 用方根估算实数的大小

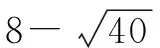
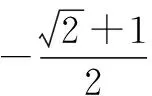
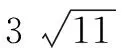
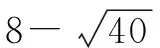
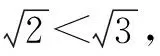
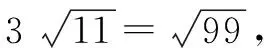
点评：估计一个数的算术平方根的大小时，应确定与这个数相邻的两个整数； 比较两个实数的大小时，先要统一标准，再比较大小．

5 用被开方数与结果的变化规律求值

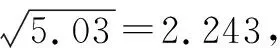
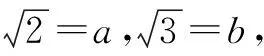
分析：算术平方根与被开方数的变化规律，即被开方数的小数点每向右(或左)移动两位，则它的算术平方根的小数点相应地向右(或左)移动一位 ．

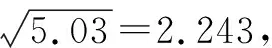
又(±44.86)2=2 012, 所以x=±44.86.

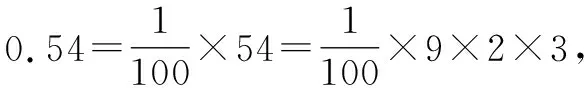
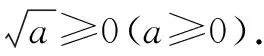
解：记

点评：利用算术平方根的双重非负性，往往是挖掘题目隐含条件和进行求解的常用方法．这类问题有一定的综合性和难度，特别对于初学“实数”的学生来说要细心体会，从本质上把握．

7 练习设计

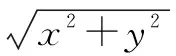
(2)已知一个正数x的平方根分别为a+1和a-3，求x；

(3)解方程8(x-1)3=27;

(2)a=1，x=4；

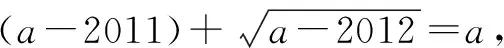
例题教学要重视问题的变式，设计好问题之间的关联，如本文中的几个问题，在牢固掌握方根的概念及本质的前提下，由易到难，通过有层次有梯度的问题串联，进行概念的对比鉴别与运用，培养学生的符号意识、抽象能力、运算能力、数据观念以及应用意识等核心素养．Z