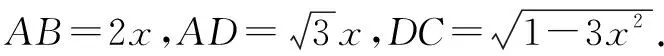灵活运用判别式巧解题

⦿江苏省盐城市亭湖初级中学 孙 东

“解一元二次方程”是人教版九年级上册第二十一章第二节的教学内容.通过本节的学习，学生掌握了解一元二次方程最基本的三种方法，其中公式法中常用到的判别式Δ=b2-4ac的意义和作用十分重大.判别式不仅能够判断一元二次方程是否有解，更重要的是，利用判别式解题是一种便捷、实用的方法，灵活运用判别式能够解决代数式变形、解方程、解(证明)不等式、解三角等许多问题.

下面通过典型例题说明灵活运用判别式解题的方法与技巧.

1 构造方程巧证明

对于含有字母类较复杂的代数恒等式证明题，当直接证明有困难时，可以巧妙地运用判别式，通过构造法将其变形为一元二次方程的形式，用代入或代换的方法完成证明.

例1已知a，b，c均为实数，且a-b=8，ab+c2+16=0.求证：a+b+c=0.

证法1：已知a-b=8，则a=b+8，所以有

(b+8)b+c2+16=0.

即(b+4)2+c2=0.

解得b=-4，c=0，a=4，所以a+b+c=0.

证法2：由于a+(-b)=8，a·(-b)=c2+16，因此以a，-b为根的一元二次方程是

x2-8x+c2+16=0.

①

由a，b，c均为实数，知其判别式

Δ=(-8)2-4(c2+16)≥0.

则4c2≤0，即c=0.从而方程①为x2-8x+16=0，故a=4，b=-4.所以a+b+c=0.

方法与技巧:证法1采用的是代入法；证法2把题设改写成a+(-b)=8，a·(-b)=c2+16，把a，-b看成了一个一元二次方程的根，构造一个一元二次方程，灵活运用判别式法，更富有技巧性.

2 变形巧解方程组

判别式本来是适用于只含有一个未知数的一元二次方程，对含有两个以上未知数的方程组似乎无能为力；但是我们如果换个视角，把方程组看作或变形为只含有一个未知数的一元二次方程，也可运用判别式法求解.

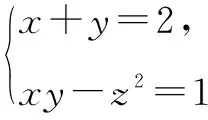
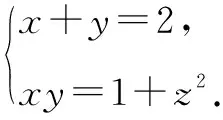
②

把②的x，y看作是一个关于m的一元二次方程的两个根，得新方程m2-2m+1+z2=0，则Δ=(-2)2-4(1+z2)=-4z2≥0，即z=0.

将z=0代入②，得x=y=1.

所以原方程组的实数解为x=1，y=1，z=0.

方法与技巧：本题是一个含有三个未知数的方程组，用常规的方法求解比较困难，但是通过观察发现方程组中有x+y与xy的特殊形式，于是设法将其变形为一个新的一元二次方程，然后用判别式法巧妙求解.

3 活用整除巧求值

对某些复杂的需要解方程的求值类问题，可以根据“判别式是完全平方数”，将其形式转化为不定方程后，再灵活应用整除的理论来求解.

例3设m是不为零的整数，关于x的二次方程mx2-(m-1)·x+m=0有有理根，求m的值.

解：Δ=(m-1)2-4m=m2-6m+1.

因为方程有有理根，所以m2-6m+1是完全平方数.设k是非负整数,且

m2-6m+1=k2.

③

则(m-3)2-8=k2，即(m-3)2-k2=8，于是

(m-3+k)(m-3-k)=8.

④

因为m-3+k，m-3-k是整数，且m-3+k≥m-3-k，所以它们可以取得的数值对应如下：

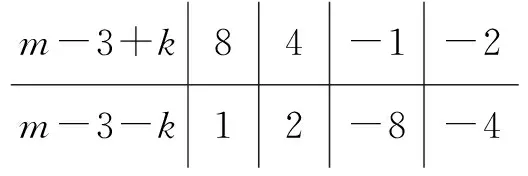
m-3+k84-1-2m-3-k12-8-4

.

将m-3+k与m-3-k相加，并考虑到m-3也是整数，且m≠0，可得m=6.

方法与技巧:解答本题的关键是根据“判别式是完全平方数”，列出如同③式这样含有多个未知数的不定方程，再把它转化成④式这样的特殊乘积形式“(……)×(……)=整数”，再应用整除理论巧妙获解.

4 巧变函数为方程

如果令二次函数的解析式为0，就能将二次函数的有关问题转化为一元二次方程的问题，就能用判别式法求解了.

例4对任意实数x，二次三项式2kx2-4x+k-1的值皆为正，求实数k的取值范围.

解：设y=2kx2-4x+k-1.因为对任意实数x，函数值y皆大于0，所以相应二次函数的图象在x轴上方开口向上，且方程2kx2-4x+k-1=0无实根.则有

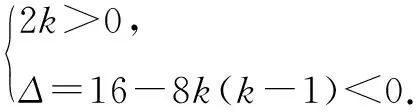
解得k>2.

方法与技巧:将二次三项式中的x看作变量，即可得到二次函数y=ax2+bx+c，且y>0.利用二次函数图象性质，即图象与x轴无交点，得到相应的判别式小于0，从而顺利求得k的取值范围.

5 巧解三角形

在解三角形问题中，可根据三角形的性质和边角关系，将几何问题转化为解一元二次方程的问题[1]，灵活运用判别式解决问题.

例5△ABC中，∠B=60°，且∠B所对的边b=1，求其余两边和的最大值.

解法1：令y=a+c，x=c.

在△ABC中，由余弦定理，得

AC2=AB2+BC2-2·AB·BC·cosB.

即12=x2+(y-x)2-2x(y-x)cos 60°.

化简整理，得3x2-3y·x+(y2-1)=0.

因为x是实数，所以Δ=(-3y)2-12(y2-1)≥0.

又因为y>0，所以0

故a+c的最大值为2.

图1

解法2：如图1，作AD⊥BC于点D，设AB=c，BC=a，BD=x.

所以

12x2-6xy+(y2-1)=0.

因为x是实数，所以Δ=(-6y)2-48(y2-1)≥0，即y2≤4，故|y|≤2.因为y>0，所以0

故0

方法与技巧:通过观察我们发现，题目涉及到三角形的两边和夹角，所以解法1由余弦定理即可求出与a+c有关的函数解析式，最后运用判别式即可求出最大值；解法2作出BC边上的高，通过解两个直角三角形，得出与AB+BC有关的函数解析式进而解决问题.

从上述各例的技巧分析中可以看出，灵活运用判别式“五巧法”能够化繁为简，快捷地解决多种数学问题，具有极大的优越性与实用性.在教学中要适当拓展、训练这些方法与技巧，提高学生的综合解题能力.