二次函数中动点图形的面积最值问题探究
⦿扬州大学数学科学学院 胡雅雯
1 真题呈现
[2021年重庆市中考数学(B卷)第25题]如图1所示,在平面直角坐标系中,抛物线y=ax2+bx-4(a≠0)与x轴交于点A(-1,0),B(4,0),与y轴交于点C.
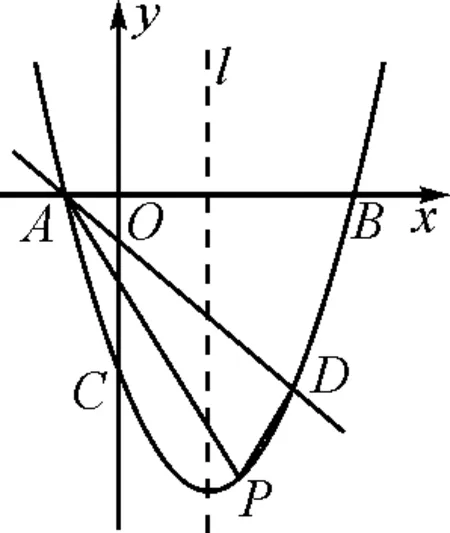
图1
(1)求该抛物线的解析式;
(2)直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛物线上一动点,连接PA,PD,求△PAD面积的最大值.
2 解法探究

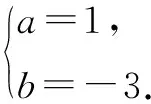
所以,该抛物线的解析式为y=x2-3x-4.
本题第(2)问可采取以下解法.
2.1 补形法
2.1.1 解法提炼
在平面直角坐标系中求“斜”△APD的面积时,可以将该三角形补形为一个易于计算面积的“规则图形”,然后将补后图形的面积与所补图形的面积相减,从而得出结果.此种方法可化未知为已知、化复杂为简单,实现巧妙求解.
2.1.2 试题解析
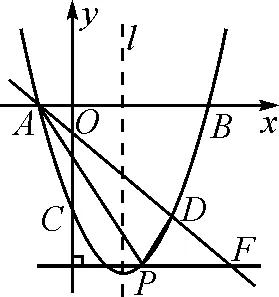
图2
如图2所示,过点P作PF垂直于y轴,交AD的延长线于点F.易求得直线AD的解析式为y=-x-1.
因P为直线AD下方抛物线上一动点,故设P(m,m2-3m-4)(-1 故PF=-m2+3m+3-m=-m2+2m+3. 所以S△APD=S△APF-S△PDF =-2(m-1)2+8. 所以当m=1时,△PAD面积的最大值为8. 2.2.1 解法提炼 如图3所示,过△APD的三个顶点分别作出与水平线垂直的三条直线,则外侧两条直线之间的距离a就叫作△APD的“水平宽”,中间这条垂线与AD相交于点E,则线段PE的长度h就叫作△APD的“铅垂高”.由此可以得出一种计算三角形面积的方法: 图3 即三角形的面积等于其水平宽与铅垂高乘积的一半[1]. 2.2.2 试题解析 如图4所示,过点P作PE垂直于x轴交直线AD于点E,易求得C(0,-4),D(3,-4)及直线AD的解析式为y=-x-1.因点P为直线AD下方抛物线上一动点,故设P(m,m2-3m-4)(-1 PE=-m-1-(m2-3m-4)=-m2+2m+3. =-2(m-1)2+8. 所以当m=1时,△PAD面积的最大值为8. 图4 2.3.1 解法提炼 本题可利用点到直线的距离公式求出△APD的高,然后结合配方法,求得高的最大值或直接求△APD面积的最大值. 图5 推导:如图5所示,设AD所在的直线方程为y=kx+b,过点P作AD的垂线PG,垂足为G,则直线PG的解析式为 2.3.2 试题解析 易求得AD的斜率k=-1.因点P为直线AD下方抛物线上一动点,故设P(m,m2-3m-4)(-1 =2|-m2+2m+3| =-2(m-1)2+8. 所以当m=1时,△APD面积的最大值为8,此时P点的坐标为(1,-6). 2.4.1 解法提炼 如图6所示,在△APD中,底边AD是确定的,平移直线AD,当其与抛物线相切于点P时,AD边上的高取最大值,即△APD的面积取最大值. 图6 2.4.2 试题解析 如图7所示,过点P作PG⊥AD,PH垂直于x轴,分别交AD于点G,H.过点P作直线l1平行于AD,当l1与抛物线相切时,AD边上的高PG取最大值. 易求得C(0,-4),D(3,-4)及直线AD的解析式为y=-x-1,故设直线l1的解析式为y=-x+n. 图7 令Δ=4-4(-n-4)=0,解得n=-5. 所以l1的解析式为y=-x-5,点P的坐标为(1,-6),点H的坐标为(1,-2),此时高PG取到最大值,最大值为 PG=PH·sin∠PHD =PH·sin 45° 即当点P的坐标为(1,-6)时,△PAD面积的最大值为8. 2.5.1 解法提炼 ax2+(b-k)x+c-m=0. 2.5.2 试题解析 如图8所示,过点P作PK垂直于x轴,交x轴于点K,过点D作DM垂直于x轴,交x轴于点M.根据上述“中横结论”得 图8 所以P(1,-6)时,S△APD取最大值,此时 S△APD=S△APK+S梯形MDPK-S△ADM 即当点P的坐标为(1,-6)时,△PAD面积的最大值为8. 2.6.1 解法提炼 “于函定理”:如图9所示,在抛物线y=ax2+bx+c(a≠0)上任意取三点A,P,D,过P作对称轴的平行线,交直线AD于点E,设PE长为d,点A,D到直线PE的垂线段长分别为m1,m2,则有d=|a|·m1·m2[3]. 图9 利用“于函定理”,可以推导出一种新的计算三角形面积的公式. 简证:由图可知, 由“于函定理”,得d=|a|·m1·m2. 显然有m1=|x1-x2|,m2=|x2-x3|, m1+m2=|x1-x3|. 2.6.2 试题解析 由(1)求得该抛物线的二次项系数a=1. 因点P为直线AD下方抛物线上一动点,故设P(m,m2-3m-4)(-1 =2|m-3||-1-m| =-2(m-3)(m+1) =-2(m-1)2+8. 即当m=1时,△PAD面积的最大值为8,此时点P的坐标为(1,-6). 综合分析以上六种解法,数形结合与转化思想是破解此类问题的“金钥匙”.在解题时,一是要以转化思想为引领,合理构造辅助线,将几何问题代数化,复杂问题简单化,实现由形转数;二是要以数形结合思想为桥梁,将抽象的数学语言与直观的图形相结合,使抽象问题具体化,实现由形析数.此外,二次函数中动点图形的面积最值问题题目变化无穷,且上述解题方法在最优题型适用上存在一定差异,建议教师在教学中既要带领学生深入剖析题目本质,也要引导学生熟练掌握以上解法,以便灵活应对不同题目.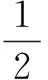
2.2 “铅锤高,水平宽”面积法
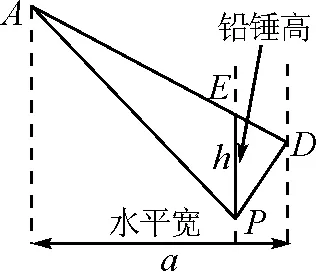
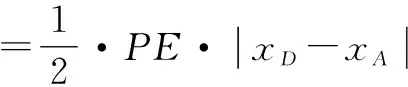
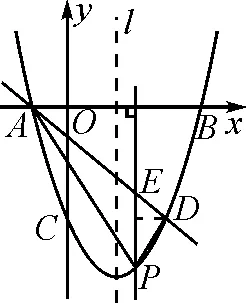
2.3 公式法

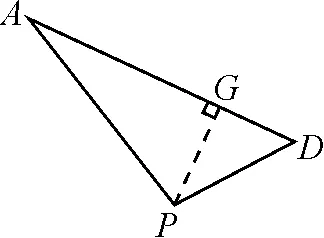

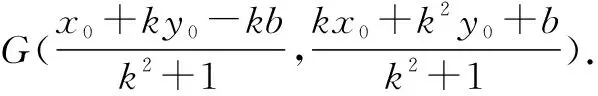
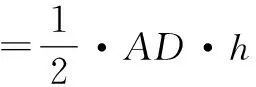

2.4 切线法


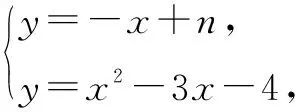

2.5 “中横结论”法
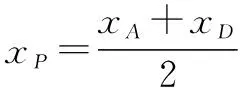
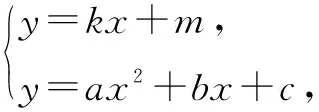
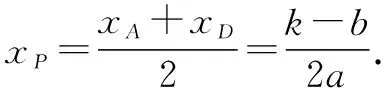

2.6 “于函定理”法
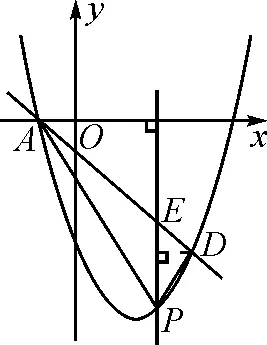
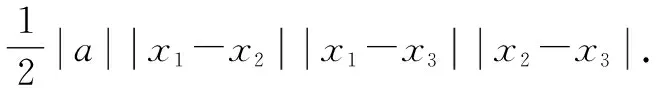
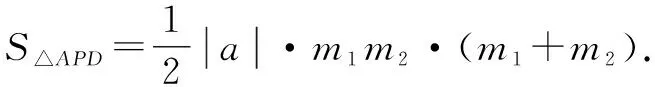
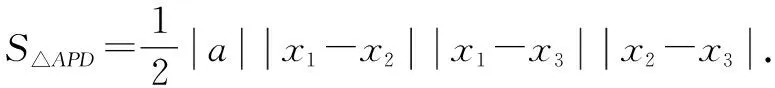
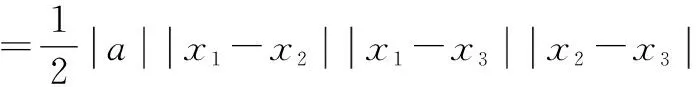
3 解题感悟

