信息适应性分层粒化的多标签特征选择

王一宾，缪佳李，程玉胜

（安庆师范大学 计算机与信息学院，安徽 安庆 246133）

随着信息技术的高速发展，多标签数据高维性问题逐渐引起了人们的关注[1]。如何从原始高维特征空间中选取较低维度的高效特征子集是机器学习、模式识别和数据挖掘等领域的一个研究热点。在多标签数据的分类过程中，学习类之间存在的层次关系可以有效提高分类精度，提升算法性能。例如，Jônatas等在树状结构和有向无环图（DAG）结构基础上，将神经网络中数据分为全局和局部层次以同步处理全局和局部信息流及其损失函数，从而提出了层次化的多标签分类网络[2]。在数据的层次结构上结合粒计算（GrC）可以有效帮助算法学习并提取特征与标签间的相关性，这一过程可以通过获取数据信息来实现，即信息粒化。GrC是以粗糙集为基础模型，其主要思想是结合人的模糊认知过程，从不同角度、不同层次对数据进行处理[3]，并选择合适的粒度解决问题。例如，Wang等通过结合样本的分类间隔和标签权重进行邻域粒化，构造了多标签邻域信息度量方法，并提出了基于信息粒化的多标签特征选择算法[4]。Li等利用最大相关性最小冗余性原则确保所选特征子集包含最多的类，在区分信息的同时表现出最小的内部冗余，结合粒度帮助探索标签依赖性，提出了基于互信息的最大相关最小冗余准则的多标签粒度特征选择方法[5]。可以发现，现有特征选择算法在信息粒化的过程中，信息熵更多的是用来计算互信息，并作为一种相关性度量方式辅助算法对特征是否被选择进行判断，而互信息大小在分层及粒化的过程中并未被充分利用。在现实生活中，信息常用于表示事物现象及其属性标识的集合。例如，针对西瓜优劣的问题，人们常用西瓜果肉的“甜度”作为一个标准，而“甜度”的高低是相对的，说明此现象的认知是一种经验结合实际的大致推测。基于对此现象的思考，我们发现模糊认知可以辅助数据的层次化分析，因此，本文利用粗糙集和人的模糊认知定义特征相关性的模糊互信息[6-7]大小来作为划分特征层次的依据，在信息层面对特征进行有向无环图的结构层次划分，并构造粒度空间完成特征选择。由于层次划分是相对模糊的，代表着每一层次的特征空间都会有强弱分化。

基于以上研究，为充分利用与特征相关的互信息，本文利用模糊互信息来度量特征重要性存在的信息差异性并将其作为特征分层的判断依据，随后在DAG基础上提出了适应特征信息的分层模型，并构造层次内部特征粒度空间以进行冗余性特征选择，提出了信息适应性分层粒化的多标签特征选择算法（MFS-IHGr）。

1 基础概念

1.1 传统信息熵

定义1[7]设随机变量A={a1,a2,a3,…,aq}，其不确定期望为令那么A的信息熵为

定义2[7]设另一个随机变量B={b1,b2,b3,…,bk}，令则A和B的联合信息熵可定义为

定义3[7]在已知B的条件下，A的条件信息熵为

定义4[7]条件熵用于衡量在已知随机变量B的条件下，随机变量A的信息不确定程度。在得到随机变量B的信息时，随机变量A的则熵减少，其减少的量即为A和B的互信息：

显然，I(A;B)是用来衡量A和B的统计相关性的，当I(A;B)=0时，A和B相互独立，此时二者之间没有提供任何信息。

1.2 模糊互信息

传统信息熵具有度量随机变量不确定性的功能，其在保留传统信息熵功能的同时，利用粗糙集中等价划分的思想，使其具有了补的性质。为帮助对特征空间进行有效的层次划分，本文引入了模糊信息熵。

定义5[5]假设信息系统用样本和其对应的特征描述，把样本空间的描述记为论域U，根据某种特征属性可以对论域U进行划分。若按照特征属性F={f1,f2,f3,…,fn}对论域U进行划分，记为U/F={A1,A2,A3,…,Am}，则模糊信息熵定义为

其中，E(A)为模糊信息熵，Aci是Ai的补集，即Aci=U-Ai，||Aci是Aci的个数，||Ai是Ai的个数表示等价类Ai在论域U中的概率表示Ai在论域U中的互补概率。将论域U中A的概率记为p={p1,p2,p3,…,pm}，则有E(p)=E(A)，即E(p)可表示为

在多标签学习中，按照特征属性对论域U的划分记为X={x1,x2,x3,…,xm}，按照标签属性对论域U的划分记为Y={y1,y2,y3,…,yn}。

定义6[5]类似传统联合熵，模糊联合信息熵定义为

定义7[5]模糊互信息可以利用自信息及模糊联合信息熵表示为

2 基于特征分层的多标签特征选择

2.1 信息适应性分层决策模型

标签的层次化分析多是语义层次的划分，而由于特征的描述多为连续型数据，语义信息在映射至标签空间前不足以划分层次。在特征选择中，更多关注特征是相关特征还是无关特征，且相关特征中亦会存在特征相关性强弱的判定。故在对特征空间进行分层时，可类比标签分层的语义关系，将层次内部特征根据强弱相关性进行划分，即信息适应性分层决策模型（模型1），具体过程如图1所示。为避免多次遍历搜索特征，可以先对原始特征空间进行特征预排序，即计算原始特征空间特征与标记空间的模糊互信息并降序排列得到特征序列F及其对应模糊互信息E(F)。将E(F)最大值作为标准，设置比例参数z，根据参数z按预排序结果搜索标准特征模糊互信息大小比例范围内的特征作为该层次的“强相关”粒度空间，范围外的特征作为“弱相关”粒度空间。本文着重于降低“弱相关”粒度空间内的特征冗余性[8]，故分化的“弱相关”粒度空间内部特征不再进入下层空间。为防止层次过多而导致粒度空间内的特征数量过于稀疏，模型内将设置断出比例参数w，当层次内部分化粒度空间内的特征数量低于原始空间与该比例参数w的乘积，则停止分层。该模型为有向决策树结构，经过冗余选择后，算法整体结构可构成有向无环图。

图1 信息适应性分层决策模型

2.2 信息适应性分层粒化的多标签特征选择

在本文算法中，对于模型1所获得的特征粒度空间，可利用最大相关性最小冗余性原则[9]进行特征选择。利用传统互信息计算粒度空间内的特征间相似性并升序排列，以一定比例选择各粒度空间的特征子集。由于模型1中设置了参数w，所以最底层粒度空间特征相关性最强但数量较少，冗余性较弱，故对最底层粒度空间特征不做选择。对于层次靠前的粒度空间，相关性较弱且数量较多，而冗余性较强，需剔除大量冗余特征，中间层次则需适量选择[10]。MFS-IHGr算法前两层选择粒度空间10%大小的特征，除最底层外其余空间选择80%大小的特征。算法框架如图2所示，具体步骤如下。

图2 MFS-IHGr算法框架

算法1信息适应性分层粒化的多标签特征选择

1)根据式（8）计算特征与标记的模糊互信息，并获得特征相关性排序，设置参数z和w；

2)fork=1:10

3)p=(z*k)

4) whilefi∈F&&E(fi)<(p*E(f1))，do

5) for eachfi∈F#fi的集合即为第k层的“弱相关”特征粒度空间Gk

6)F=F-Gk

7) ifGk的特征数量d′≤(w*d)#d为原始特征数量

8)Gk=F;break

9) end

10) end

11)end while

12)end

13)根据式（4）计算特征间标准互信息，得到每个粒度空间的冗余性降序特征序列。根据设置的比例，选择靠前的特征作为各层次空间特征子集，并合并为最终目标特征集合。

3 实验数据及其结果分析

3.1 实验数据和相关参数设置

本文采用Birds、Business、Computers、Education、Recreation和Reference 6个数据集来验证算法的有效性，实验数据均来自http://mulan.sourceforge.net/datasets.html，相关信息如表1所示。实验代码均在Matlab2016a中运行，硬件环境为Intel®Core(TM)i5-9600K 3.70 GHz CPU，16 G内存，操作系统为Windows10。实验选用4个常用多标签学习评价指标来综合评价算法性能，分别是平均精度（AP）、覆盖率（CV）、汉明损失（HL）和排序损失（RL）[11]，其中AP值越大越好，而CV、HL和RL值越小越好。

将本文所提算法与MDDMproj[12]、PMU[13]、MFS-MCDM[14]和MFMNIpes[7]进行比较。其中，MDDMproj是根据原始特征与标签空间最大相关性将原始数据投影到较低维的特征空间；PMU是使用互信息作为特征度量标准的早期经典算法之一，至今仍具有一定优势；MFS-MCDM则将多标签特征选择作为一个信息融合过程，通过计算每个标签的熵来得到一个加权决策矩阵，再利用TOPSIS方法对每个特征进行排序，并根据具体需求进行特征数量的选择；而MFMNIpes是根据人的认知观点定义邻域概念，将邻域信息熵推广到适应多标签学习，并给出新的邻域互信息措施，从而通过近似多标签邻域互信息求解优化目标函数。在上述算法中，MDDMproj和PMU并未考虑特征冗余性；而MFS-MCDM和MFMNIpes只将互信息用作度量工具且忽略了特征信息中可能存在的层次结构。

对于MDDMproj算法，δ参数设置为0.5。本文信息适应性分层决策模型中描述的比例参数z设置为z∈(0,1)，断出比例参数w设置为w∈(0,1)，取值间隔为0.1。其中，z控制层次粒度空间特征数量，w控制层次数量。在实验中，40%的样本用于训练，60%的样本用于测试，并使用KNN作为分类器验证算法性能。将ML-KNN[15]平滑系数设置为1，最近邻数k设置为10。本文算法所得子集特征数量固定，其他对比算法获得的特征数量随机。为了更好地观测最终特征子集的指标变化情况，其他算法都使用与本文算法所选择特征数目一致的特征子集。

3.2 实验结果分析

实验结果如表2所示，最优结果以黑体显示。可以发现，在6个数据集的24个结果中，MFS-IHGr算法仅在Recreation数据集的整体结果欠佳，其余结果除Brids数据集的HL指标较差以外，均表现为最优或次优。在AP、CV和RL指标中，MFS-IHGr算法均在4个数据集上达到了最优性能，故而MFS-IHGr算法总体表现优秀。

表2 在AP、CV、HL和RL4个指标上的5种特征选择算法实验结果

本文算法设置了两个超参数z和w，并以Birds数据集为例进行了参数敏感性分析[16]，如图3所示。可以发现，算法性能在不同参数下成块状分布，即在两个参数的某个取值范围内实验结果无明显变化。这是因为参数z和w本质上是帮助模型进行特征的层次划分，而本文的划分方法是根据特征本身携带的信息决定的，所以在一定程度上反映出数据存在的特征层次数量是不一致的。对于不同的层次划分，算法的指标精度变化也证明了本文算法对特征空间分层学习的有效性。

图3 基于Birds数据集的参数敏感性分析

3.3 统计假设检验

本文采用显著性水平α=0.05下的Nemenyi检验[17]测试了所提算法与其他算法的性能。当两个对比算法在所有数据集上平均排序的差值大于临界差值，则认为这两个算法存在显著性差异，否则无显著性差异。临界差值的计算公式如下：

其中，K=5，N=6，qα=2.728 0，临界差值为2.490 3。

图4给出了在4个指标上每种算法间的对比情况，对于没有显著性差异的算法用实线相连，各评价指标从左至右，算法性能依次降低。可以看出，MFS-IHGr算法与其他算法相比，除MFS-MCDM算法以外，显著性差异并不明显，但仍具有一定优势，各项指标的平均排序排名均第一。这说明虽然MFS-IHGr算法具有一定的性能优势，但与其他算法的竞争力较弱，存在改进空间。

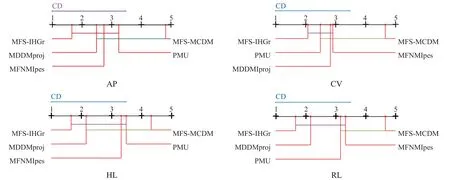
图4 各种算法的性能比较

4 结论

本文提出了信息适应性分层粒化的多标签特征选择算法（MFS-IHGr），在利用模糊互信息充分衡量了特征相关性的同时，也利用标准互信息解决了粒度空间内部特征冗余性。然而，由于MFS-IHGr算法是基于DAG结构的分层模型，从实验结果来看，并不是所有数据集都适用于该结构的分层选择。例如Recreation数据集的实验结果整体表现极差，而Reference数据集的实验结果整体表现极好。在下一步工作计划中，我们将提出更具普适性的分层多标签特征选择算法。