基于控制参数分群的DFIG 并网系统低频振荡抑制

李生虎， 张奥博， 颜云松， 韩 伟， 宋 闯

（1.合肥工业大学 电气与自动化工程学院， 安徽 合肥 230009； 2.南瑞集团有限公司 国网电力科学研究院有限公司， 江苏 南京 211106； 3.国网河南省电力公司电力科学研究院， 河南 郑州 450052）

0 引言

随着大规模风电并网， 风电机组如双馈感应发电机（Doubly-Fed Induction Generator，DFIG）与同步发电机（Synchronous Generator，SG）间动态交互可能加剧电网振荡，增加新的振荡模式[1]～[5]。

低频振荡（Low-Frequency Oscillation，LFO）一般指频率在0.1～2.5 Hz，且阻尼比小于阈值的振荡模式，特征值分析可以确定电网振荡特性[6]。 文献[7]考虑了风电场在运行风速、接入容量以及参与无功调度的不同情况，基于特征值分析了LFO 模态的振荡特性。文献[8]从风电输送距离、联络线传送功率等方面研究了DFIG 并网对振荡特性的影响。文献[9]，[10]分别描绘了特征值随锁相环、虚拟惯量控制参数变化的轨迹， 分析了系统振荡的变化。加装电力系统稳定器（Power System Stabilizer，PSS）、静止无功发生器等装置，可以提高电力系统稳定性[11]～[14]。 文献[15]在DFIG 上安装功率振荡阻尼器， 采用时域仿真验证加装装置对系统振荡的抑制效果。但是大部分控制器结构复杂，引入系统会增加投资和保护的成本。 调节风电系统中的控制参数， 如DFIG 变流器内部的PI 参数[16]，[17]，SG励磁器参数等[18]，也能抑制系统振荡。 文献[19]发现系统振荡阻尼受DFIG 电流内环控制参数影响较大，控制参数的整定可以抑制振荡。 基于先进优化算法，处理系统中的控制参数，可用来研究风电系统稳定分析和最优控制。 文献[20]，[21]采用粒子群算法， 以临界阻尼比最大化为目标函数，对PSS 的参数进行优化。 但是系统中有多种控制参数， 对全局控制参数优化会增加经济成本，且部分控制参数对振荡抑制能力有限，因此需要考虑如何选择主导参数。

特征值灵敏度可用来评估参数调节对LFO的控制效果[22]～[24]。 文献[25]，[26]分别计算阻尼比对发电机有功、无功的灵敏度，通过灵敏度指标确定发电机调度最有效的方式， 调节发电机出力，增强临界模式的阻尼。文献[27]推导了特征值对DFIG-PSS 传递函数的灵敏度表达， 分析表明，与参数灵敏度相比，传递函数灵敏度精度更高。文献[28]时域仿真结果表明，对基于灵敏度选择的主导参数优化， 可以更好地抑制系统振荡。文献[29]对多台发电机按有功调制方向进行同调性分群，可采用类似方法根据参数对系统阻尼调节效果进行分群。

本文建立DFIG 并网电力系统小扰动稳定分析模型。 根据模式振荡频率和阻尼比，筛选LFO模式。 建立危险模式阻尼比对控制参数灵敏度的解析表达。基于模式危险程度和阻尼比灵敏度，定义累积阻尼比灵敏度， 描述控制参数对多个模式阻尼比的总体调节效果。考虑风速与负荷波动，以场景分布概率作为权系数， 对不同场景的累积阻尼比灵敏度加权累加。 引入模糊C 均值（Fuzzy C-Means，FCM）聚类算法，按调节效果对控制参数进行分群。 最后给出小扰动分析和时域仿真结果， 验证了所选主导参数对LFO 模式的抑制效果。

1 风电系统小扰动分析模型

1.1 DFIG 与SG 建模

DFIG 由风力机及其传动轴、感应电机、转子侧变流器（Rotor Side Converter，RSC）、网侧变流器（Grid Side Converter，GSC）、直流电容等构成，如图1 所示。

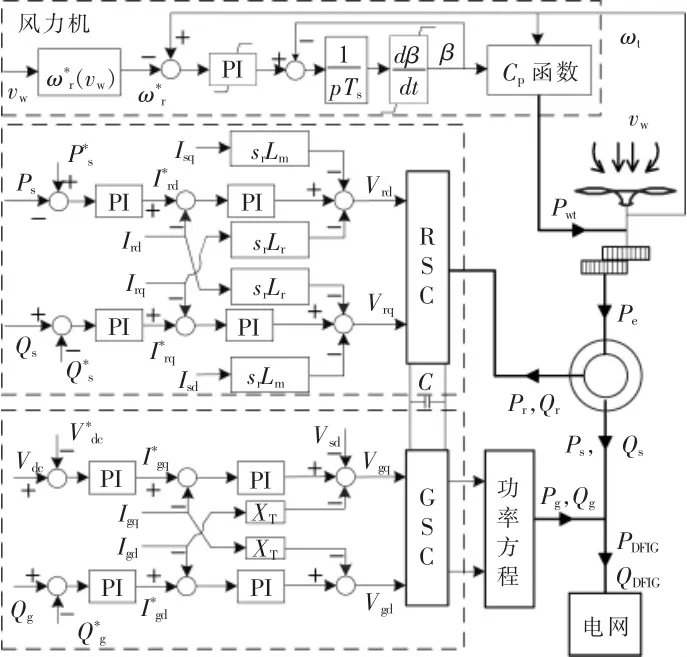
图1 DFIG 控制模型Fig.1 Control model of DFIG

风力机桨距角控制用于维持风力机转速和DFIG 有功出力。 RSC，GSC 采用双环控制。

SG 控制结构如图2 所示。

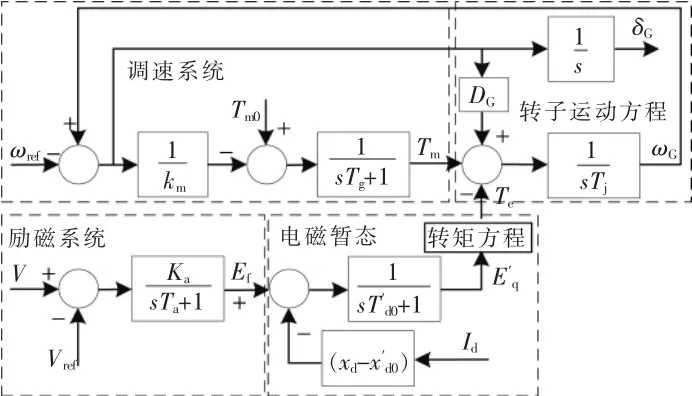
图2 SG 控制模型Fig.2 Control model of SG

图中SG 采用5 阶动态模型， 包括转子运动方程（2 阶）、转子电磁暂态（1 阶）、励磁系统（1阶）、调速系统（1 阶）。

1.2 DFIG 与SG 数学建模

DFIG 并网引入新的状态变量和代数变量，同时还存在与SG 的动态交互，即：

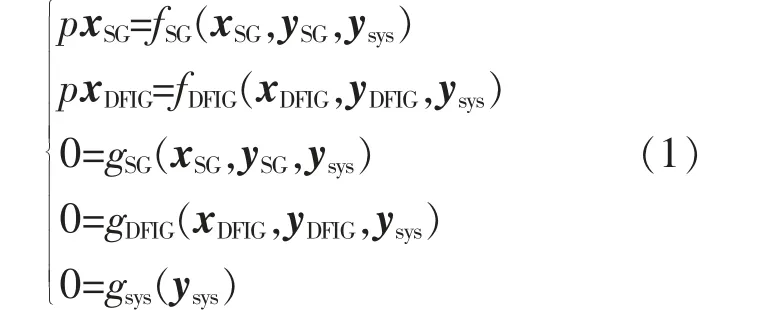
式中：x，y 分别为状态变量和代数变量的向量形式；fSG，fDFIG分 别 为SG，DFIG 状 态 方 程 的 函 数 形式；gSG，gDFIG，gsys分别为SG，DFIG，系统代数方程的函数形式；p 为微分算子。

电力系统小干扰稳定分析， 在变量稳定运行点处对系统方程作线性化处理：

式中：Asys为系统状态矩阵， 可根据Asys计算系统特征值λ、阻尼比ξ 和频率f，以及用于描述模式与状态变量相关性的参与因子pkj：

式中：pkj为第k 个状态变量对第j 个模式的参与因子；Ψ，Φ 为左、右特征向量矩阵。基于阻尼比和灵敏度可用来筛选LFO 模式。

2 累积阻尼比灵敏度和FCM 聚类

2.1 灵敏度模型

风电系统的控制参数， 包括PI 参数、SG 调速、励磁环节参数等。特征值灵敏度表征控制参数α 的改变对特征值的影响， 其中控制参数α 包括如DFIG 变流器的PI 参数、SG 调速、 励磁系统的参数等，其解析式为

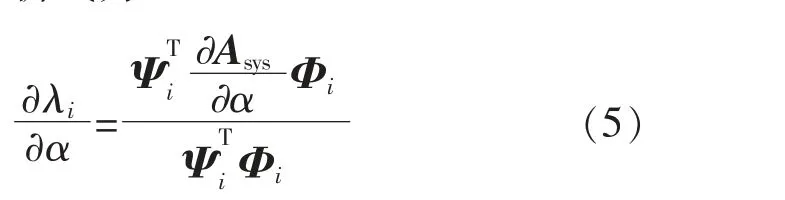
若提高LFO 模式的阻尼比，须进一步推导阻尼比对控制参数灵敏度的解析，其表达式为

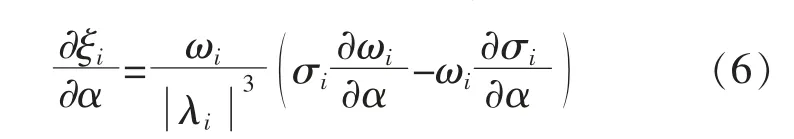
式中：ξi为特征值λi的阻尼比；σi，ωi分别为特征值的实部和虚部。

阻尼比灵敏度量化了控制参数对模式阻尼比的调节效果。 对于有不同的取值范围和物理意义的控制参数， 评价调节效果应该基于参数的相对调节范围，而不是绝对调节量。为了消除不同控制参数取值范围与量纲的差异， 引入相对阻尼比灵敏度用于选择主导参数[17]，即：

选择灵敏度数值最大的控制参数作为主导控制参数， 这样能够实现相同参数调节量对阻尼比的调节效果最好。 风电系统中有多种LFO 模式，调整控制参数很难实现对所有模式的同向调节，可能出现部分LFO 模式被抑制，而部分模式被恶化的情况。 LFO 模式的阻尼比越小，危险程度越高，这类模式应当被优先调节。可根据阻尼比与设定安全裕度ξcr的相对距离， 定义模式的危险程度。 第i 个LFO 弱阻尼模式的危险系数di为

为了描述控制参数对风电系统中LFO 模式阻尼比的总体调节效果，定义控制参数αj的累积阻尼比灵敏度Sj，其表达式为

式中：X 为LFO 模式的集合。

累积阻尼比灵敏度Sj考虑不同LFO 模式的危险程度，将阻尼比灵敏度加权累加，反映了控制参数变化时，LFO 模式阻尼比的总体变化趋势。采用模式的危险程度作为权系数， 使得阻尼比小的模式被优先调节。Sj的数值越大，表明参数对模式阻尼比的总体调节效果越好。 当参数对不同模式有相反的调节效果时， 阻尼比灵敏度的累加会相互抵消。 基于Sj筛选得到主导控制参数，通过牺牲一些危险程度低的模式，而实现LFO 模式阻尼比的总体提升。

风电系统中， 风速和负荷的波动通过影响潮流的分布，改变小干扰稳定分析计算的结果，进而改变振荡模式的分布。不同的风电场景，LFO 模式集合X 可能不同，分布概率也有差异。 基于Sj选择控制参数，可能无法适应于多个场景。因此需要划分风电场景， 保证同一场景的样本有相近的特征，而不同场景都有各自明确的特征。基于历史实测风电场数据，采用聚类算法，将具有相近特性的样本数据聚成一类，得到各个不同的风电场景。聚类中心点代表了各类的平均水平， 避免了考虑风速时刻波动的复杂运算。

本文采用FCM 聚类算法处理风速和负荷数据。为了确定适用于多个风电场景的主导参数，引入不同风电场景的概率密度作权系数， 将聚类中心作为典型风电场景， 计算每一类风电场景的LFO 模式集合， 对累积阻尼比灵敏度进行改造，即：

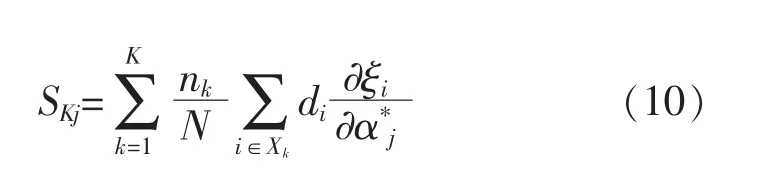
式中：nk为第k 类场景的样本数；K 为风电场景聚类数；N 为总样本数；Xk为第k 类场景的LFO 模式集合。

SKj考虑了不同风电场景、 振荡模式的变化，使控制参数对阻尼比的调节， 可能出现某些概率小的场景效果好，概率大的场景效果差的情况，还可能出现不同场景调节效果相反。 本文选择的主导参数要能够适用于更多场景， 因此将场景的概率分布设为权系数，使得在分布概率大的场景中，调节效果好的控制参数的作用更加明显。

在风电系统多个控制参数中， 确定主导控制参数，难点不仅在于推导灵敏度的解析表达，还在于高效选择控制参数。对于主导控制参数，灵敏度数值特征明显高于其他参数。 采用FCM 聚类算法， 基于累积阻尼比灵敏度， 对控制参数进行分群。累积阻尼比灵敏度数值大小，用来划分主导参数，符号用来判断调整方向。 聚类后，同一聚簇的控制参数对阻尼比有相同调整方向、 相近调节效果，通过比较不同聚簇便可确定主导参数组。只需从聚类结果中挑选出两类聚簇， 即上调主导参数簇Ωup和下调主导参数簇Ωdown， 而无需再将控制参数的灵敏度结果依次进行比较。

2.2 FCM 聚类算法

FCM 算法是基于二次目标函数最小化的迭代优化算法， 数据的隶属度基于数据距聚类中心的距离决定。 本文提供了一种用于抑制风电系统LFO 模式主导参数分群方案。 首先根据风电系统小干扰稳定分析结果，筛选LFO 模式，推导阻尼比对控制参数灵敏度的解析表达，计及模式危险程度，计算累积阻尼比灵敏度，同时引入不同风电场景的分布概率，采用FCM 算法对控制参数进行分群，得到对多模式、多场景有较好调节效果的主导参数组，具体流程如图3 所示。 本文所提算法不限于对DFIG 并网系统， 也不限于调节LFO 模式阻尼比，可用于同步发电机、改善其他振荡模式或评估指标。

图3 抑制LFO 控制参数分群流程Fig.3 Flow chart of parameters clustering to damp LFO

3 算例分析

本文采用新英格兰39 节点测试系统， 如图4所示。

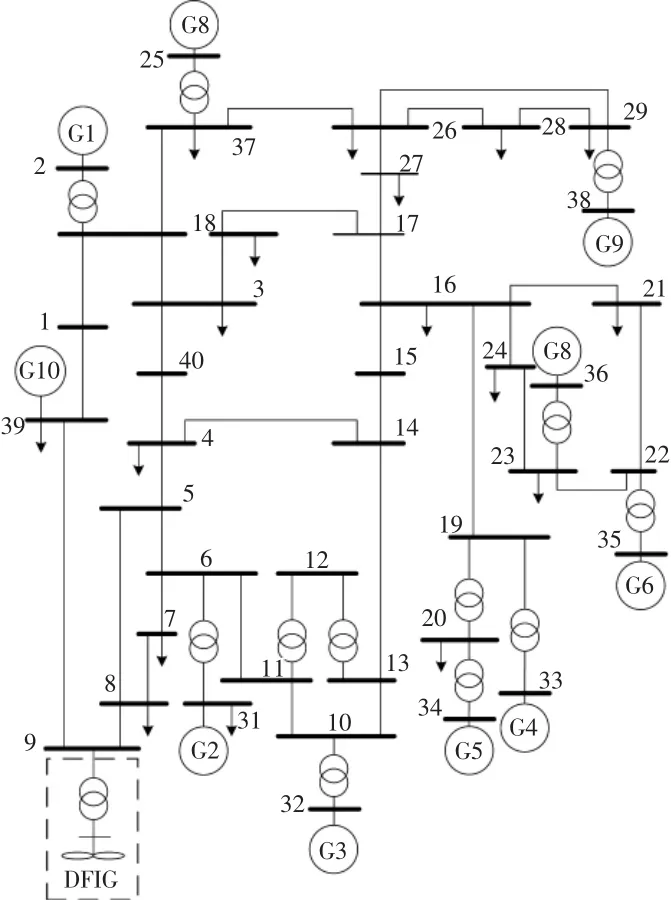
图4 新英格兰39 节点测试系统Fig.4 New England 39 node test system

风电机组经变压器并入9 号节点。 SG 控制参数如表1 所示。 DFIG 结构参数见文献[30]，[31]，PI参数如表2 所示。 基准功率为100 MV·A，初始风速为12 m/s。 阻尼比安全裕度ξcr设定为0.1[32]，[33]。

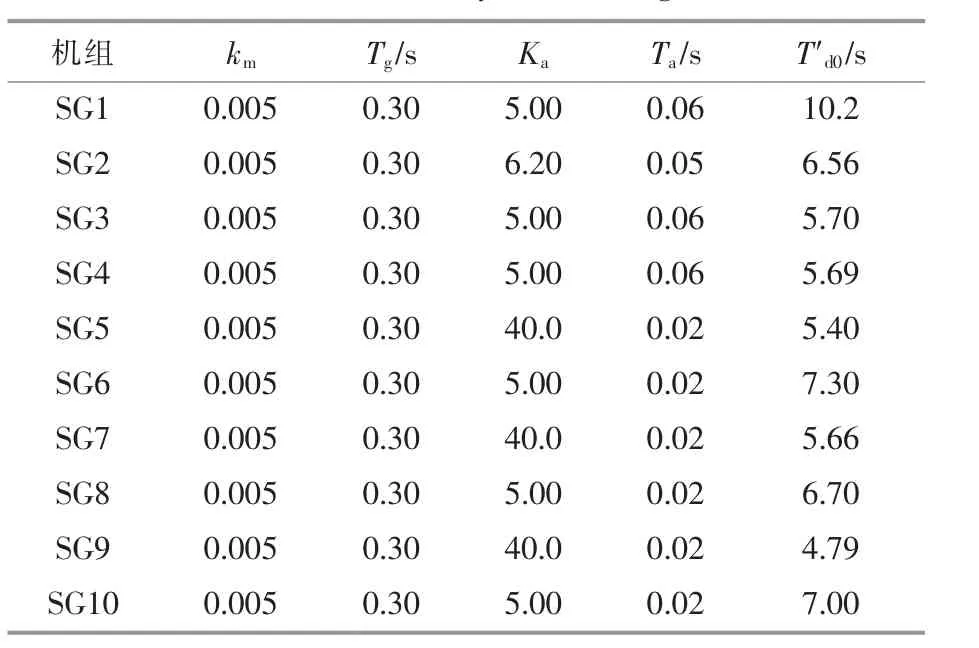
表1 同步发电机参数Table 1 Parameters of synchronous generators

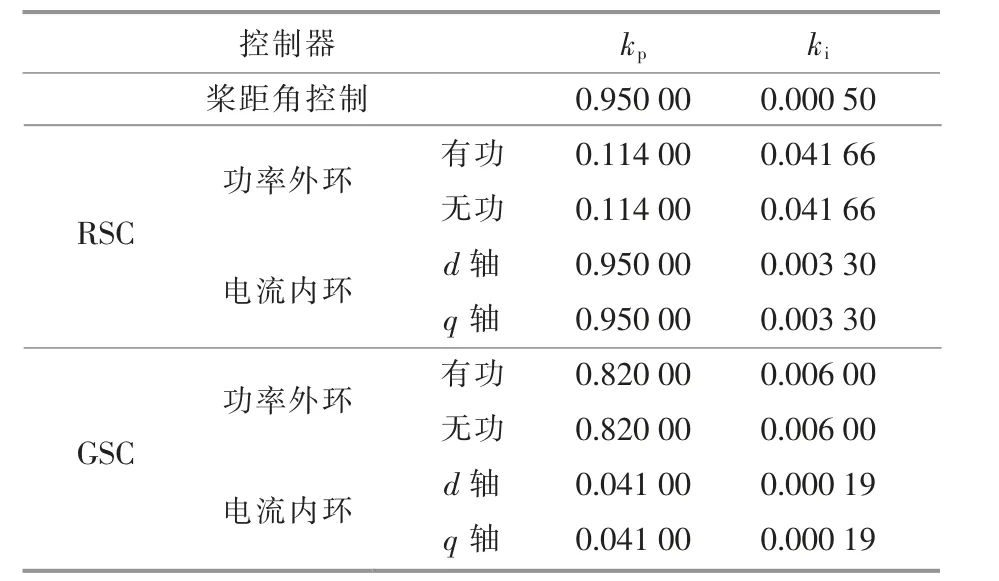
表2 PI 控制器参数Table 2 Parameters of PI controller

3.1 DFIG 并网对LFO 模式的影响

分别对DFIG 并网前后的测试系统进行小干扰稳定性分析，计算特征值、频率、阻尼比，结果如表3 所示。

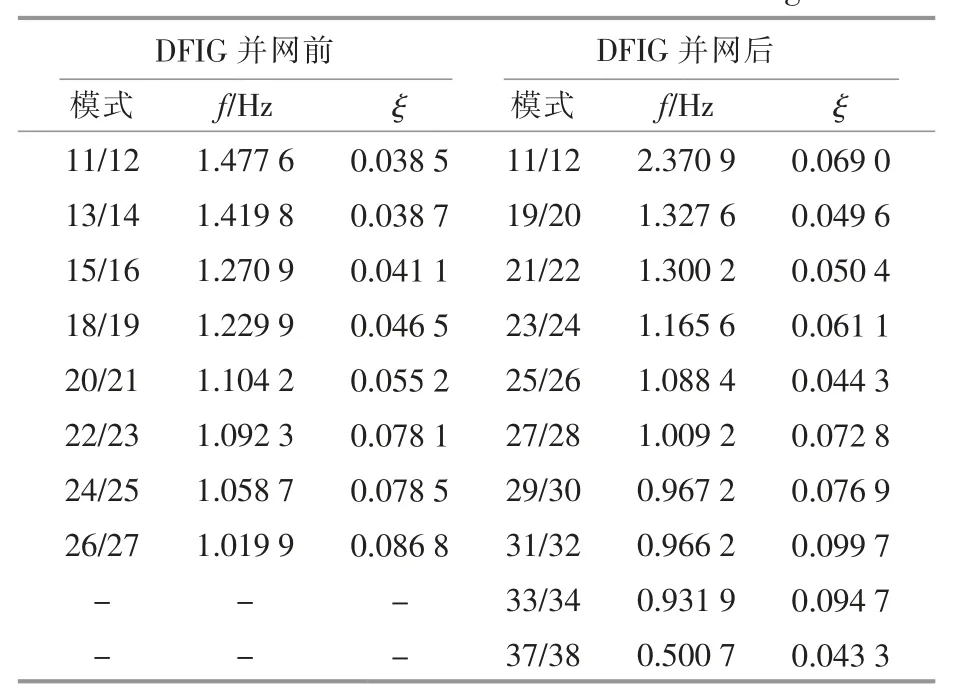
表3 DFIG 并网前、后LFO 模式Table 3 LFO modes before and after DFIG integrated

DFIG 并网前， 系统有8 个LFO 模式，DFIG并网后增加了新的LFO 模式。 由参与因子计算结果， 模式11/12，37/38 与DFIG 状态变量相关，属于DFIG 引入模式。 其中模式19/20，25/26，37/38的阻尼比小于0.05，属于LFO 弱阻尼模式，属于危险程度高的模式，需要重点关注。

3.2 基于累积阻尼比灵敏度的参数分群

表4 列出了部分LFO 模式阻尼比对控制参数的相对灵敏度计算结果。 对于DFIG 引入的LFO 模式，PI 参数调节效果要明显好于SG 的控制参数，而对于SG 相关模式，PI 参数并未有明显的调节效果，Tg的调节效果明显更优。 对于部分控制参数如ki2，根据阻尼比灵敏度结果，对模式11/12，37/38 的阻尼比都有较好的调节效果，但是调节方向相反。 在计算累积阻尼比灵敏度的过程中，两种相反的灵敏度数值相加，最终Sj的结果很小，因此不会将这类参数分群到主导参数组中。

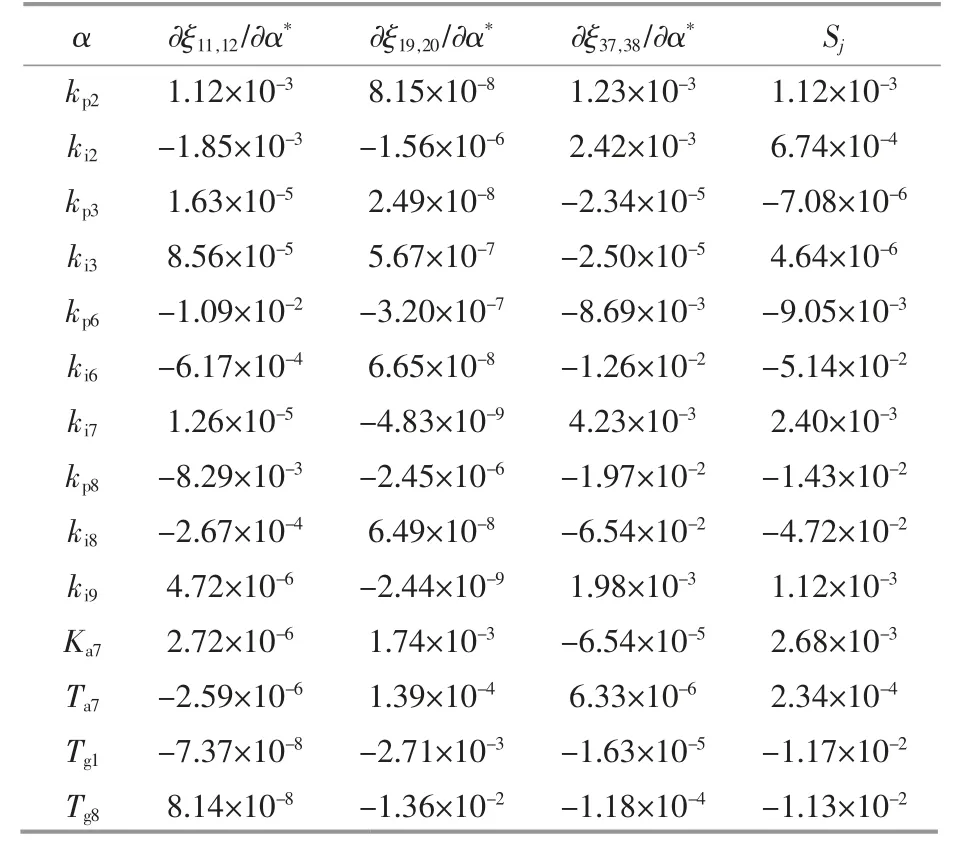
表4 阻尼比对控制参数的相对灵敏度Table 4 Relative sensitivity of damping ratio to control parameters

为验证本文所提出方法的正确性， 采用摄动法与解析法所得的灵敏度模型进行比较，以ξ25，26，ξ37，38为例，结果如图5 所示。两条曲线在初始运行点相切，验证了阻尼比灵敏度解析表达的正确性，可用于描述控制参数对阻尼比的调节效果。

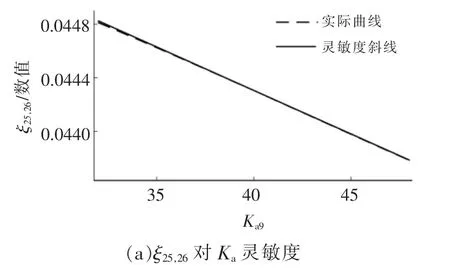
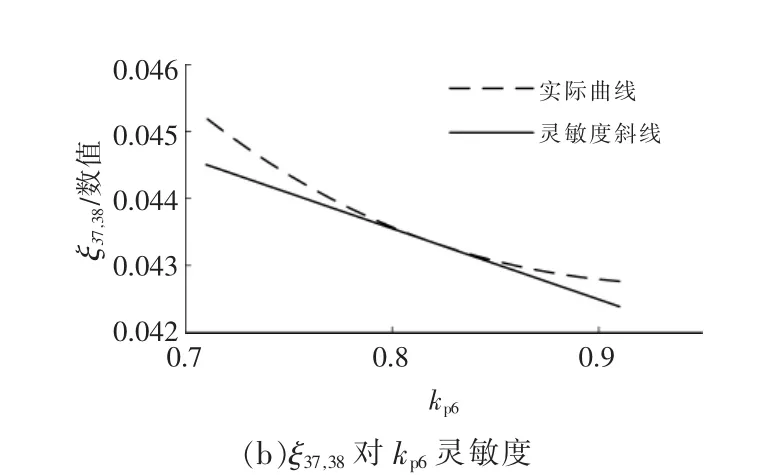
图5 灵敏度模型验证Fig.5 Validation of sensitivity model

对于DFIG 和SG 相关LFO 模式的调节，可以对PI 参数与SG 控制参数分别进行处理。 基于FCM 聚类算法对控制参数分群，选择出对LFO 调节效果最好的参数聚簇，即主导参数组，结果如表5 所示。

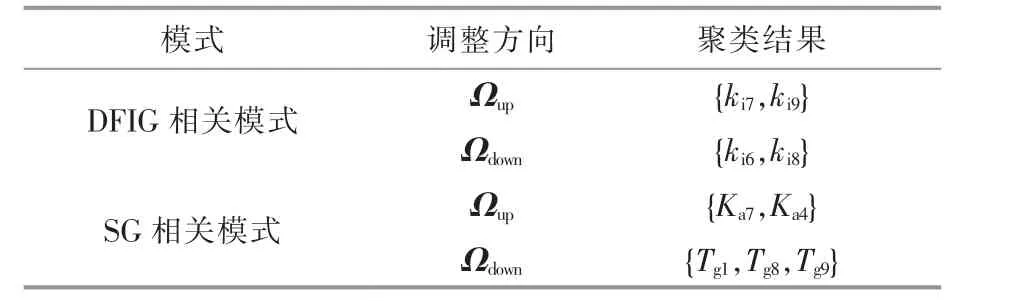
表5 基于FCM 控制参数分群Table 5 Clustering to control parameters based on FCM

为了检验本文所提控制参数分群方法， 相较于传统基于阻尼比灵敏度选择的控制参数，对LFO 模式有更好的调节效果， 采用时域仿真进行验证。设定系统7 号节点在0.5 s 时发生三相短路故障，在0.6 s 故障消除，仿真总时间20 s。 选择19/20，25/26 两种LFO 弱阻尼模式，由相关因子可知，这两种模式的强相关变量分别为ω1，ω6。 时域仿真结果如图6 所示。 通过调节基于灵敏度排序和累积相对灵敏度聚类得到的主导参数， 都能对LFO 有一定抑制作用。 而在保证所调节参数相对调节量相同的条件下， 基于累积阻尼比灵敏度聚类得到的主导参数组， 调节效果优于基于阻尼比灵敏度选择的参数， 因为基于灵敏度只能选择对本模式调节效果好的主导参数， 而基于本文方法得到的主导参数群，能够兼顾更多的LFO 模式。

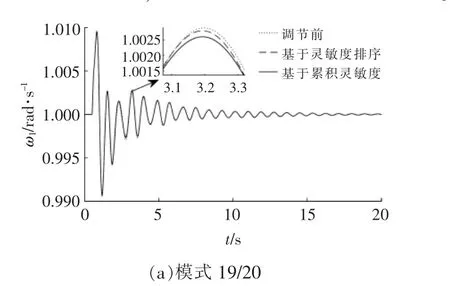
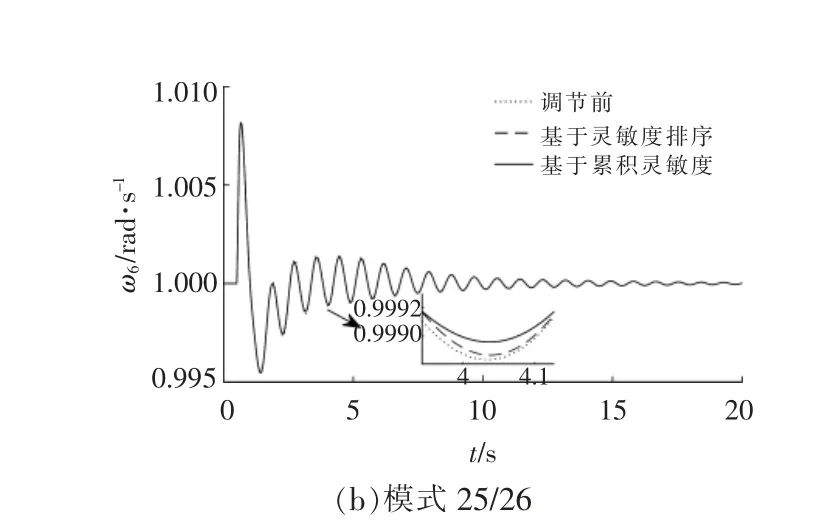
图6 调节主导参数对LFO 的抑制效果Fig.6 Damping effect of dominate parameters adjustment on LFO

3.3 多风电场景分析

在节点9 的DFIG 接入某地风电场风速数据，在节点1 处加入负荷数据。 基于FCM 聚类算法，将所得到的风速-负荷数据进行聚类，聚类得到各类的中心和样本数量如表6 所示。

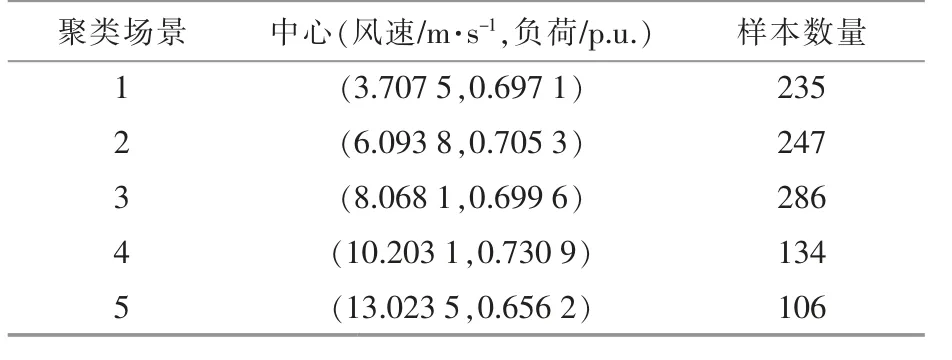
表6 聚类中心和样本数量Table 6 Clustering center and sample size

由表6 可以看出，聚类分布较为均匀，可用以描述风速的随机性与波动性数据特征。

将聚类中心作为典型风电场景，带入特征值，计算每一类场景的累积阻尼比灵敏度， 以及多场景累积阻尼比灵敏度，如图7 所示。

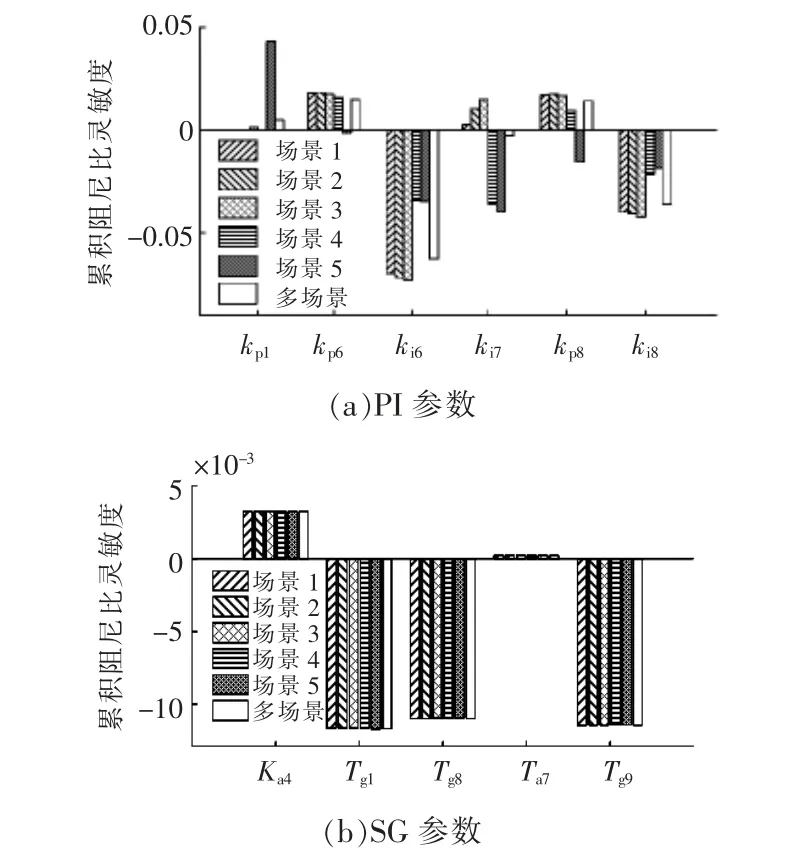
图7 多场景累积阻尼比灵敏度Fig.7 Multi-scenario cumulative sensitivity of damping ratio

随着风电场景的改变， 由于风速的改变影响更多的是DFIG 引入的振荡模式，部分PI 参数的累积阻尼比灵敏度变化较大。如kp1在场景5 累积阻尼比灵敏度数值突然增大，因为该场景下DFIG启动了桨距角控制， 但是在其他风电场景下对阻尼比提升并无贡献；ki7在不同场景下对阻尼比的调节方向不同，无法作为多场景下的主导参数。图7（b）中SG 控制参数在不同风电场景下累积阻尼比灵敏度数值变化不大， 因为灵敏度结果与振荡模式和系统的拓扑结构有关， 而风电场景的改变对SG 相关振荡模式影响较小， 系统结构也未发生改变，因此SG 控制参数分群的结果影响不大。对于PI 参数，基于单一场景的累计灵敏度得到的主导参数组可能无法适用于多种场景，需对PI 参数重新分群， 使所选主导参数尽可能的适应不同场景。

基于多场景下累积阻尼比灵敏度，对PI 参数重新进行分群，结果如表7 所示。

表7 适用多场景的PI 参数分群Table 7 Clustering to PI parameters for multiple scenarios

为了验证所得主导控制参数组能适应多个风电场景，按主导参数组调整方向，对每个参数调节0.1 p.u.。 选取风速数据差距最大的场景1 和场景5，观察阻尼比的调节效果，如表8 所示。

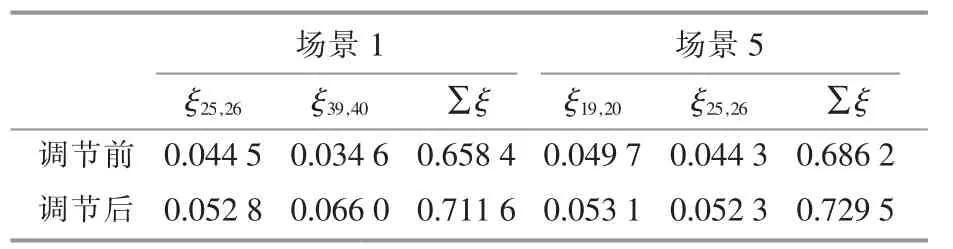
表8 调节主导参数对阻尼比的影响Table 8 Effect of dominate parameters adjustment on damping ratio

在这两个场景中， 系统阻尼比最小的两个模式和总阻尼比都是提升的， 虽然没有完全消除LFO 模式，但是提高了系统的阻尼比，有利于LFO模式的抑制。

4 结论

为改善风电系统小干扰稳定、 抑制LFO 模式，并考虑风速波动对抑制方案的影响，提出了一种基于累积阻尼比灵敏度的控制参数分群方法，得到以下结论： ①基于累积阻尼比灵敏度， 采用FCM 聚类算法对控制参数进行分群，得到控制参数组。时域仿真结果表明，相较于选择各模式参数灵敏度数值最大的为主导参数， 本文所提方案得到的主导参数组， 对LFO 抑制效果更加明显；②多风电场景下， 风速变化影响DFIG 相关振荡模式， 因此有必要引入风电场景分布概率修改累积阻尼比灵敏度。小干扰分析结果表明，调节控制参数组中主导参数，弱阻尼模式阻尼比和LFO 模式阻尼比之和在不同风电场景中都有所提升。

本文所提算法在双馈风电机组并网系统得到了应用，对于其他风电机组以及光伏并网系统，本文所提控制参数分群算法对低频振荡模式的抑制效果，可在后续研究中进一步验证。