考虑损伤判据温度相关性的相场法模拟氧化铝热冲击裂纹扩展*
杨国欣, 郑世风, 李定玉, 李卫国
(1. 重庆大学 航空航天学院,重庆 400044;2. 重庆科技学院 建筑工程学院,重庆 401331)
引 言
陶瓷材料在服役历程中常常面临复杂热冲击环境,由于陶瓷材料固有的脆性致使其抗热冲击性能较差[1-3],往往会伴随热冲击裂纹的产生,导致材料失效.材料热物理性能参数和损伤判据的温度相关性,给揭示宽温域热冲击过程中热冲击破坏的内在机理带来了挑战[4-5].在实验研究方面,氧化铝陶瓷是常用的代表性材料之一,水淬实验是研究陶瓷热冲击行为广泛使用的方法,如Shao 等[6]的实验研究中,先将氧化铝陶瓷板加热到不同的热冲击初始温度,然后自由落体于室温下的水中,结果表明初始温度越高陶瓷板在淬火过程中热冲击破坏更严重,且呈现出大量长短相间分布的平行裂纹.另一种常用于研究陶瓷热冲击行为的方法是圆盘辐射加热实验,如Honda 等[7-8]开展了红外辐射加热氧化铝陶瓷圆盘的实验,圆盘中心的圆形区域被辐射加热,中心加热区域大小和热流密度不同,实验观察到了不同类型的裂纹扩展路径.在数值模拟方面,相场法由于能够很好地模拟热-力学、化学-力学等多物理场耦合下的裂纹扩展问题,能够方便地预测裂纹的起裂位置、扩展路径以及裂纹的相交和分叉,成为近年来裂纹演化模拟的常用方法[9-12].Chu 等[13]建立了热-力耦合相场模型,分别对Shao 等[6]开展的氧化铝陶瓷薄板水淬实验和Honda 等[7-8]开展的圆盘辐射加热热冲击实验进行了模拟,该模拟结果很好地再现了陶瓷薄板水淬实验中的长短裂纹和圆盘辐射加热热冲击裂纹的扩展和分叉.但是水淬实验中不出现裂纹的地方在该模拟结果中出现了密集的短裂纹,圆盘辐射加热实验的模拟中圆盘加热区域大小对裂纹分叉位置的影响也没有很好地体现.他们采用室温下的临界能量释放率作为损伤判据,而裂纹萌生和扩展时裂纹尖端通常处于宽温域的热环境,鉴于临界能量释放率具有较强的温度依赖性[14],因此,在使用相场法模拟复杂热冲击环境下热冲击破坏行为时有必要考虑损伤判据的温度相关性.本文在现有热力学相场模型的基础上通过引入温度相关性损伤判据,修正了相场模型的控制方程,并对氧化铝陶瓷开展了热冲击裂纹扩展相场有限元模拟研究.
1 考虑温度相关性损伤判据的相场有限元模型
利用一维模型(图1)来描述扩散裂纹拓扑的变分原理,考虑横截面为A长度为L的无限扩展的杆,假设杆在轴向位置x=0 处出现裂纹,其中 Γ为裂纹面,这种尖锐的裂纹拓扑结构可以用辅助场变量d¯(x)∈[0,1]来描述,d¯=0表 示材料完好的状态,d¯=1表示材料完全损伤的状态.
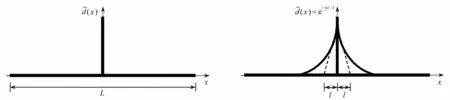
图1 x=0 处尖锐和弥散裂纹拓扑:(a)尖锐裂纹;(b) 弥散裂纹,用长度尺度l 表示裂纹相场d¯Fig. 1 Topologies of sharp and diffuse cracks at x=0: (a) the sharp crack; (b) phase field d¯ of the diffuse crack denoted by length scale l



2 有限元仿真结果及分析
2.1 Al2O3 薄板水淬热冲击
Shao 等[6]水淬实验所建立的有限元几何模型如图2 所示,对一半的陶瓷板采用对称性边界条件建模,模型中选用的网格为四边形网格,网格尺寸为0.025 mm.对其热冲击裂纹扩展过程进行模拟并和实验结果相比较.模拟过程中所需的材料参数如表1 所示.平板的初始温度为680 K,水温在300 K 保持恒定,计算时试件与水的热交换系数取值为50 kW/(m2·K)[6].

表1 氧化铝薄板试样材料参数[6]Table 1 Material parameters of the alumina sheet sample[6]
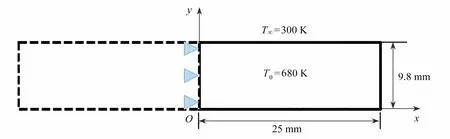
图2 水淬实验几何模型Fig. 2 The geometric model for the water quenching experiment
图3 为模型对称约束边中点在不同网格密度下x方向最终的应力结果,对模拟结果进行了收敛性分析.其中l0=0.1 mm, 随着网格的细化,模拟结果逐渐趋于一致性,采用的网格尺寸为 0.25l0时与网格尺寸为0.1l0的模拟结果最大误差小于0.5%,满足有限元计算精度要求,网格的极细化虽然可以取得更为精确的结果,但是会极大地增加运算量,因此后续的数值模拟中网格尺寸选为0 .25l0.
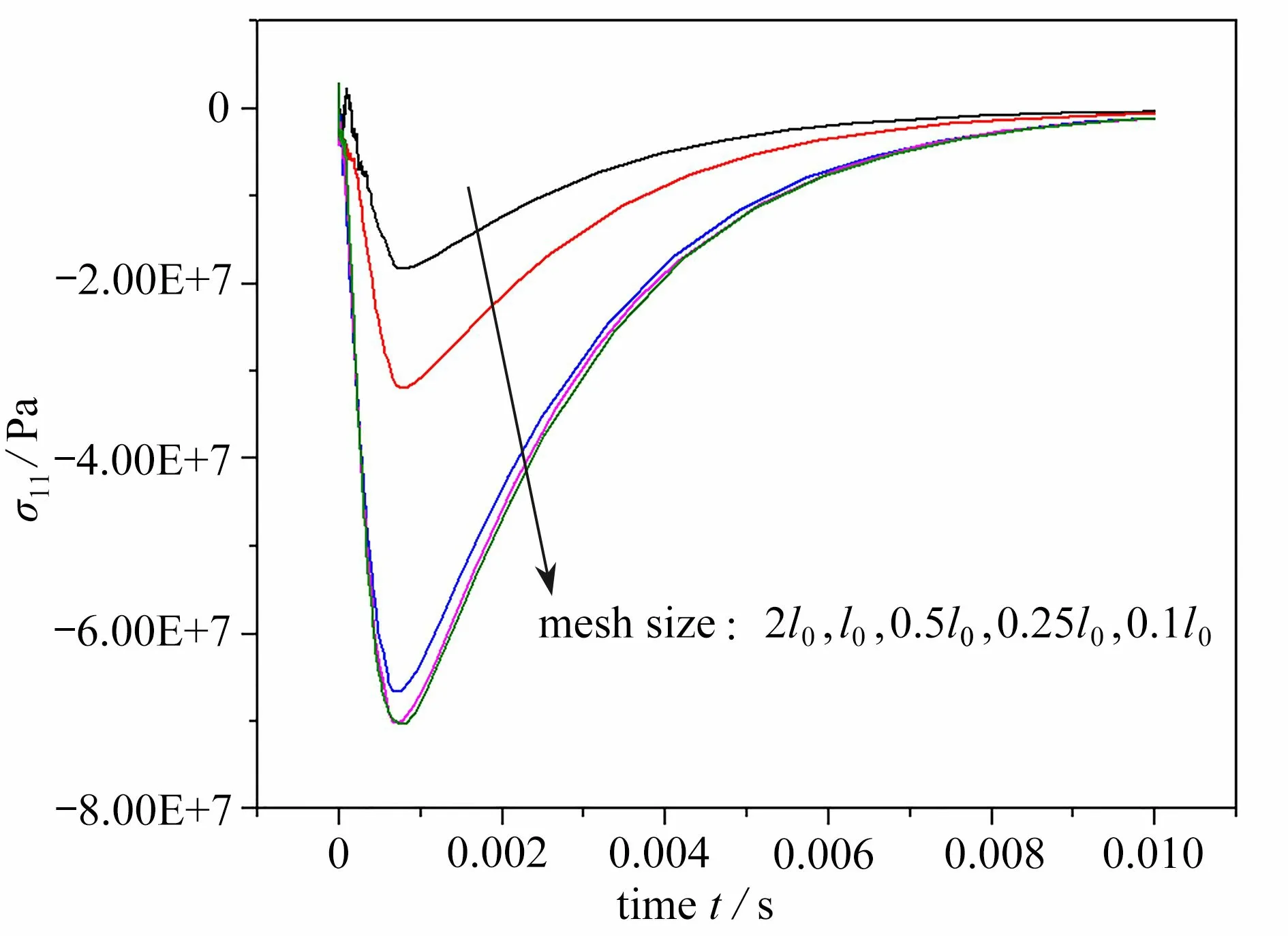
图3 收敛性分析Fig. 3 Convergence analysis
初始温度为680 K 时,热冲击过程中裂纹萌生和扩展过程如图4(a1)、4(b1) 、4(c1) 、4(d1)所示.最初在热冲击边界处萌生出一定数量间隔相当的平行短裂纹,如图4(a1)、4(b1)所示,随着时间的推移所有裂纹均继续扩展,如图4(c1)所示,当裂纹扩展到一定长度后,一部分裂纹停止扩展,另一部分裂纹继续扩展到最终长度后停止扩展,形成长短相间分布的平行裂纹形貌.温度场随时间的演化过程如图4(a2)、4(b2) 、4(c2) 、4(d2)所示,在t=8.5E-3 s 裂纹停止扩展时,分别提取了不同长度裂纹尖端的温度如图4(d1)所示,温度跨度在318.26 K ~636.57 K.裂纹扩展过程中尖端温度场表明裂纹扩展时裂纹尖端会经历宽温域的热环境,说明在模拟过程中有必要考虑损伤判据的温度相关性.
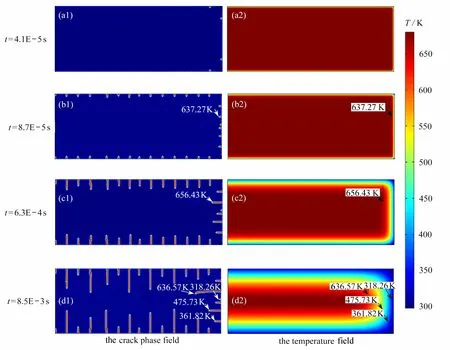
图4 裂纹相场和温度场随时间的演化Fig. 4 Evolution of the crack phase field and the temperature field with time
图5 给出了水淬实验结果与有无考虑温度相关性损伤判据模拟结果的对比,图5(a)为Chu 等[13]不考虑温度相关性临界能量释放率的模拟结果,图5(b)为Shao 等[6]的水淬实验结果,图5(c)为本文考虑温度相关性临界能量释放率的模拟结果.从结果中可知,有无考虑温度相关性损伤判据均能模拟出水淬实验中长短相间分布的平行裂纹(以长度超过红线的裂纹为长裂纹[6]),且长裂纹在扩展长度和间距上均与实验结果吻合较好.图5(a)中不考虑损伤判据温度相关性的模拟结果中在边界出现了Shao 等的实验结果中未见报道的密集短裂纹,致使其模拟出的边界处裂纹密度远高于实验结果.事实上裂纹的萌生与扩展需要一定的能量,当某个位置萌生了裂纹时,由于裂纹萌生和扩展使裂纹附近一定区域内能量得到消耗,故在已萌生裂纹临近的一定区域内不再有足够的能量使新裂纹萌生.本文通过考虑损伤判据的温度相关性,模拟出的裂纹密度与试验取得了更好的一致性,说明考虑温度相关性损伤判据的模拟结果与实验结果吻合得更好.

图5 水淬实验结果与有无考虑温度相关性损伤判据模拟结果的对比:(a) Chu 等[13]的模拟结果;(b)实验结果[6];(c) 本文模拟结果Fig. 5 Comparison between water quenching experimental results and simulation results with or without temperature-dependent damage criteria:(a) simulation results of Chu et al [13]; (b) the experimental results [6]; (c) simulation results of this paper
2.2 圆盘试样中心辐射加热热冲击
本文考虑损伤判据的温度相关性,对Honda 等[7-8]开展的红外辐射加热氧化铝陶瓷圆盘实验进行了有限元模拟,分析了热流密度和加热半径对裂纹扩展路径的影响,并与Chu 等[13]未考虑损伤判据温度相关性的模拟结果进行比较.表2 给出了试样温度相关性材料参数,根据前文所做收敛性分析选取自由三角形网格尺寸为0.025 mm,有限元几何模型如图6 所示,a表示辐射加热区域的加热半径, γ表示辐射加热的热流密度,外界环境温度为室温293.15 K,非加热区域采用对流换热.

表2 圆盘试样的温度相关性材料参数[7-8]Table 2 Temperature-dependent material parameters of disk samples[7-8]
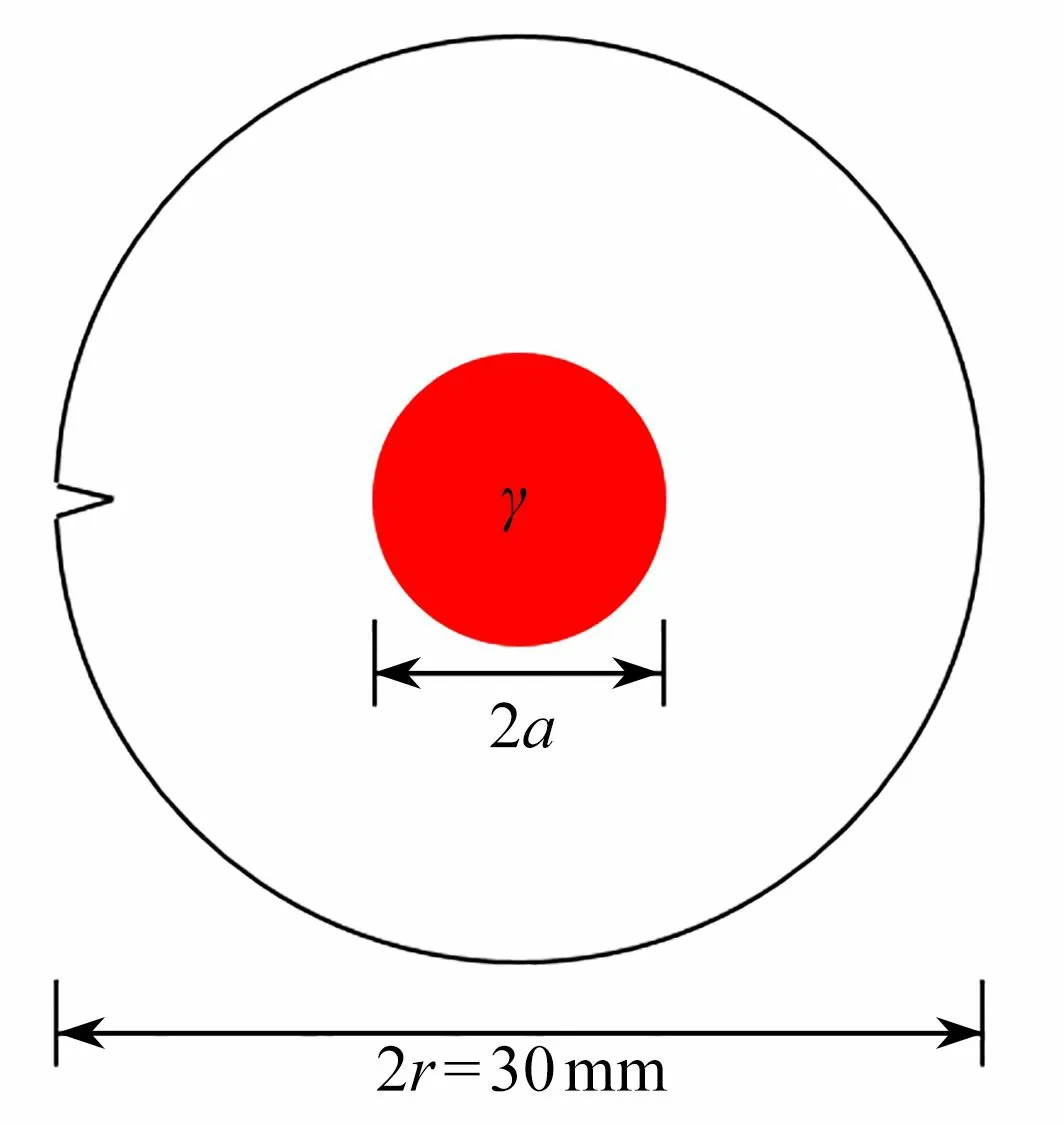
图6 圆盘热冲击问题的几何模型和热边界条件(红色区域表示外加热流)Fig. 6 The geometric model and thermal boundary conditions for thermal shock problems of disks (the red area represents applied heat flow)
图7 给出了辐射加热实验结果和相场模拟结果的对比,图7(a1)、7(b1)、7(c1)为辐射加热的实验结果[7-8],图7(a2)、7(b2)、7(c2)为Chu 等[13]不考虑温度相关临界能量释放率的有限元模拟结果,图7(a3)、7(b3)、7(c3)为本文考虑临界能量释放率温度相关性的有限元模拟结果.有限元模拟的加热区域半径均为7.5 mm,热流密度 γ =2.5×105kW/m3和 γ=7.5×105kW/m3时,有无考虑损伤判据温度相关性的模拟结果均与实验结果取得较好的一致性.当有限元模拟的加热区域半径为5 mm,圆盘中心热流密度γ =7.5×105kW/m3时,不考虑损伤判据的温度相关性的模拟结果中裂纹的分叉位置发生在加热区域内部,如图7(c2)所示,考虑损伤判据的温度相关性的模拟结果(图7(c3))中虽然也会在中心形成分叉裂纹,但是主裂纹的分叉位置与实验结果均发生在加热区域外部.由于实验中没给出加热区域的热流密度,为了对比不同热流密度对较小加热区域圆盘热冲击裂纹模拟结果的影响,开展了加热区域半径为5 mm、热流密度γ =1×106kW/m3的有限元模拟,模拟结果如图8 所示.
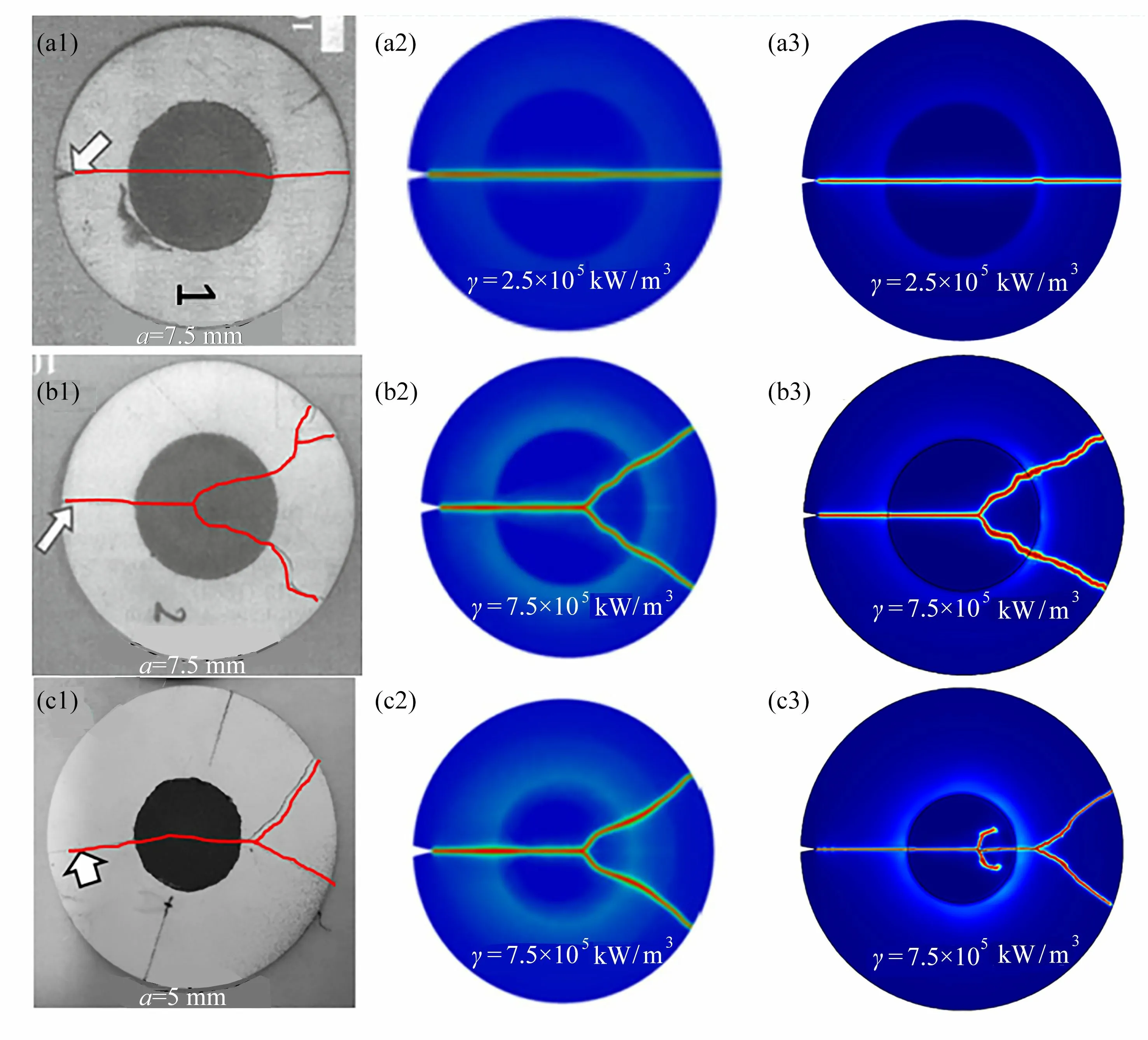
图7 圆盘辐射加热实验结果和模拟结果Fig. 7 Experimental results of radiation heating and simulation results of the phase field method
图8 给出了加热区域半径为5 mm 圆盘辐射加热实验结果与模拟结果的对比.图8(a)为实验结果;图8(b)为热流密度 γ =1×106kW/m3,考虑损伤判据温度相关性的模拟结果,很好地模拟出了实验结果的裂纹形貌,且裂纹分叉位置均出现在加热区域外部;图8(c)为同样加热条件下不考虑损伤判据温度相关性的模拟结果,此时主裂纹的分叉位置出现在加热区域内部.
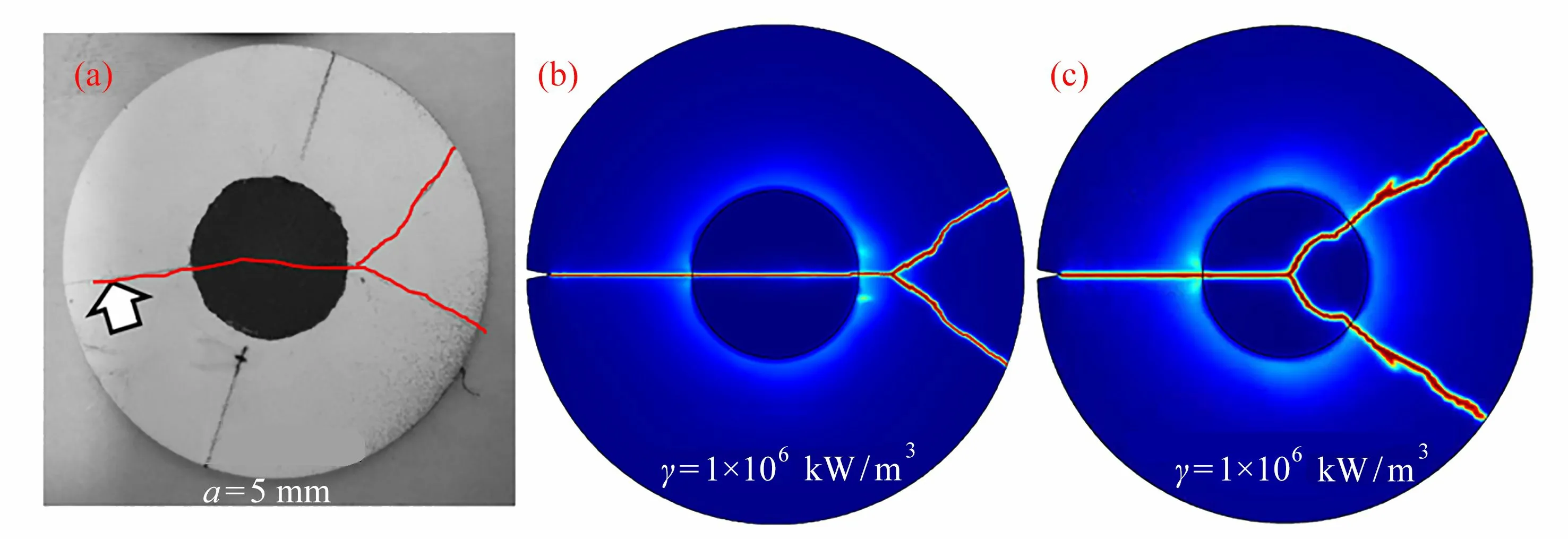
图8 圆盘辐射加热实验结果和模拟结果: (a)实验结果;(b) 考虑温度相关性临界能量释放率Gc(T)的模拟结果;(c) 不考虑温度相关性临界能量释放率Gc 的模拟结果Fig. 8 Experimental and simulation results of disk radiation heating: (a) the experimental results; (b) the simulation results with temperature-dependent critical energy release rate Gc(T); (c) the simulation results without temperature-dependent critical energy release rate Gc
图9 为加热区域半径5 mm,考虑损伤判据温度相关性不同热流密度下的裂纹和裂纹尖端温度随时间的演化.由图9(a)可知当裂纹开始扩展时(t=0.001 993 s),裂纹尖端温度为293.84 K,当裂纹扩展到加热区域内部时(t=0.002 01 s),加热区域内部的裂纹尖端温度达到439.95 K;而图9(b)中裂纹在加热区域内部分叉时(t=0.015 943 s),裂纹尖端温度为450.31 K,裂纹扩展过程中裂纹尖端经历了宽温域的热环境,充分说明了考虑损伤判据温度相关性的必要性.
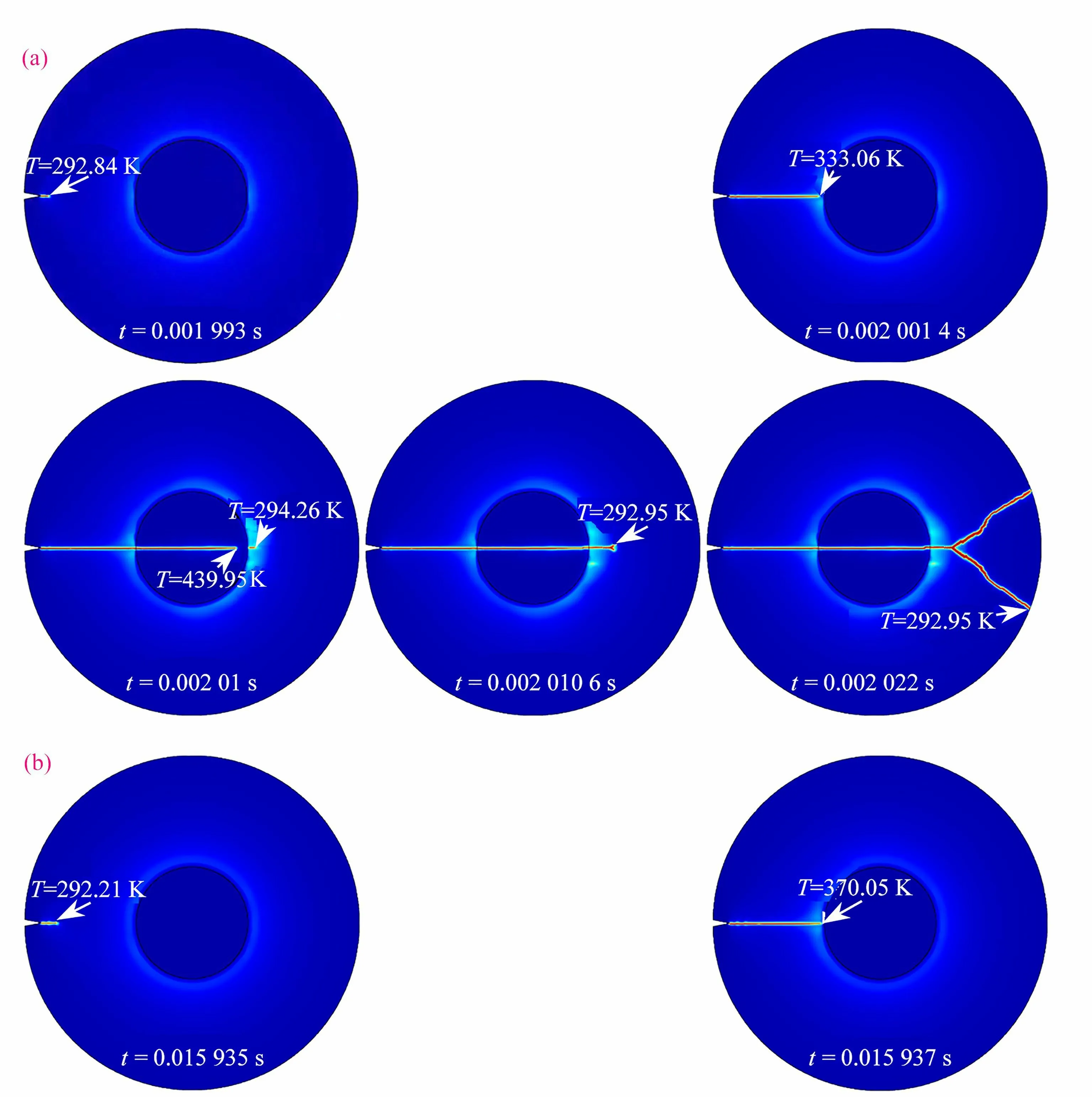
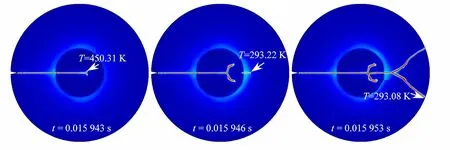
图9 不同热流密度下的裂纹和裂纹尖端温度随时间的演化:(a) γ =7.5×105 kW/m3 ;(b)γ=1×106 kW/m3Fig. 9 Evolution of crack and crack tip temperatures with time under different heat fluxes: (a) γ =7.5×105 kW/m3 ; (b)γ=1×106 kW/m3
3 结 论
本文在现有热力学相场模型的基础上通过引入温度相关性损伤判据,修正了相场模型的控制方程.分别对氧化铝薄板水淬实验和圆盘辐射加热实验进行了相应的数值模拟,并与实验结果及不考虑损伤判据温度相关性的模拟结果进行了对比.发现考虑损伤判据温度相关性的模拟结果很好地再现了水淬实验中多裂纹扩展以及长短相间分布的平行裂纹,且未出现不考虑损伤判据温度相关性模拟结果中试件边缘密集短裂纹.当加热区域为5 mm 时,考虑损伤判据温度相关性很好地模拟出了圆盘辐射加热实验结果的裂纹形貌,且主裂纹的分叉位置与实验结果裂纹分叉位置均出现在加热区域外部,而不考虑损伤判据温度相关性的模拟结果中主裂纹分叉位置发生在加热区域内部.模拟结果表明,模拟中考虑温度相关性损伤判据,实现了对宽温域下热冲击裂纹的萌生和扩展过程更合理的模拟,为研究材料在复杂热冲击环境下的失效机理提供了一种有效手段.
参考文献( References ) :
[1]KINGERY W D. Factors affecting thermal stress resistance of ceramic materials[J].Journal of the American Ceramic Society, 2010, 38(1): 3-15.
[2]MENOUILLARD T, BELYTSCHKO T. Analysis and computations of oscillating crack propagation in a heated strip[J].International Journal of Fracture, 2011, 167: 57-70.
[3] 吴大方, 王怀涛, 朱芳卉. 1 200 ℃高温环境下部件受热前表面应变的光学测量[J]. 应用数学和力学, 2018, 39(6):631-644. (WU Dafang, WANG Huaitao, ZHU Fanghui. Optical measurement of heated-front-surface strains for components in high temperature environments up to 1 200 ℃[J].Applied Mathematics and Mechanics, 2018,39(6): 631-644.(in Chinese))
[4]LI D, WANG R, WANG X, et al. Simulation of the thermal shock cracking behaviors of ceramics under water quenching for 3-dimension conditions[J].European Journal of Mechanics A:Solids, 2020, 84: 104080.
[5]WU J Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure[J].Journal of the Mechanics and Physics of Solids, 2017, 103: 72-99.
[6]SHAO Y, ZHANG Y, XU X. Effect of crack pattern on the residual strength of ceramics after quenching[J].Journal of the American Ceramic Society, 2011, 94: 72-99.
[7]HONDA S, OGIHARA Y, KISHI T, et al. Estimation of thermal shock resistance of fine porous alumina by infrared radiation heating method[J].Nippon Seramikkusu Kyokai Gakujutsu Ronbunshi, 2009, 117(1371): 1208-1215.
[8]HONDA S, SUZUKI T, NISHIKAWA T, et al. Estimation of thermal shock properties for silicon nitride having high thermal conductivity[J].Journal of the Ceramic Society of Japan, 2010, 110(1277): 38-43.
[9]KARMA A, KESSLER D A, LEVINE H. Phase-field model of mode Ⅲ dynamic fracture[J].Physical Review Letters, 2001, 87: 045501.
[10] 李家宇, 曾忠, 乔龙. 相场方法模拟液滴的动态润湿行为[J]. 应用数学和力学, 2019, 40(9): 957-967. (LI Jiayu,ZENG Zhong, QIAO Long. Numerical simulation of droplets’ dynamic wetting process with the phase field method[J].Applied Mathematics and Mechanics, 2019, 40(9): 957-967.(in Chinese))
[11]MICHE C, SCHÄNZEL LM, ULMER H. Phase field modeling of fracture in multi-physics problems, part Ⅰ: balance of crack surface and failure criteria for brittle crack propagation in thermo-elastic solids[J].Computer Methods in Applied Mechanics and Engineering, 2015, 294: 449-485.
[12] 柳占立, 初东阳, 王涛, 等. 爆炸和冲击载荷下金属材料及结构的动态失效仿真[J]. 应用数学和力学, 2021, 42(1): 1-14. (LIU Zhanli, CHU Dongyang, WANG Tao, et al. Dynamic failure simulation of metal materials and structures under blast and impact loading[J].Applied Mathematics and Mechanics, 2021, 42(1): 1-14.(in Chinese))
[13]CHU D, LI X, LIU Z. Study the dynamic crack path in brittle material under thermal shock loading by phase field modeling[J].International Journal of Fracture, 2017, 208: 115-130.
[14]LI D, LI W, WANG R, et al. Simulation of the thermal shock behavior of ultra-high temperature ceramics with the consideration of temperature-dependent crack propagation criterion and interaction between thermal shock cracks evolution and thermal conduction[J].European Journal of Mechanics A:Solids, 2018, 72: 268-274.
[15]MIEHE C, HOFACKER M, WELSCHINGER F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits[J].Computer Methods in Applied Mechanics and Engineering, 2010, 199(45/48): 2765-2778.
[16] 李定玉. 计及使役环境的高温陶瓷材料抗热震性能及表征方法研究[D]. 博士学位论文. 重庆: 重庆大学, 2015. (LI Dingyu. Research of thermal shock resistance of high temperature ceramics and its characterization methods with the consideration of different operating environments[D]. PhD Thesis. Chongqing: Chongqing University, 2015.(in Chinese))

