第二类边界条件下固液相变问题的改进型准稳态近似解*

杨小虎， 李少丹， 陈 凯

（武汉第二船舶设计研究所 热能动力技术重点实验室，武汉 430205）

引 言

固液相变现象广泛存在于自然界和工业生产当中，如水（冰）的凝固（熔化）、冶金工业、热能（冷量）存储与利用[1]、电子设备或人体热防护[2]以及生物医学等领域[3].对固液相变传热问题的理论研究始于19 世纪奥地利物理学家Stefan 对极地冰熔化过程和土壤冻结问题的研究，故又称为Stefan 问题.Stefan 问题是两相耦合的具有移动边界的非线性问题，且一般为瞬态问题，这使得其理论求解十分困难.目前，仅针对少数简单情况下的Stefan 问题存在解析解，最典型的是Neumann 于1864 年首先给出的直角坐标系半无限大空间第一类边界条件（恒壁温）下一维Stefan 问题的精确解[4].

作为经典Stefan 问题的延伸，当边界条件由第一类边界条件变化为第二类边界条件（恒热流）时，其理论求解将变得十分复杂[5].Evans 等[6]采用Laplace 积分变换，并假定固液界面函数是时间的幂级数的形式，首次给出了恒热流边界条件下单相Stefan 问题的界面函数解析解表达式.Schiavone 等[7]进一步发展了这一方法并完整地给出了界面函数和温度分布的表达式.然而，这种幂级数形式的解是无界函数，且必须无限求和才能得到真正收敛的解，这在实际计算中不太适用.El-Genk 等[8]于1979 年以微分方程的形式给出了这一问题的解析解，但其不便于直接使用，而且其正确性目前也存在争议.

此外，当求解问题由直角坐标系变换到柱坐标系或球坐标系时，理论求解会变得更加困难.例如，针对工程中常见的圆柱体内（外）的相变问题，目前还没有获得精确解，实际处理中往往使用数值模拟计算.尽管数值模拟方法已经很成熟，但是使用起来比较麻烦，而且难以获得通用的无量纲解，不利于实际问题的快速分析.因此，给出形式简单的通用近似解析解对于实际问题的初步分析十分必要[9-11].目前，针对第二类边界条件下Stefan 问题的近似求解方法很多，主要包括热平衡积分近似法、摄动法、准稳态法等[4].热平衡积分法数学求解过程复杂，特别是在柱坐标下，且对很多问题给出的解是微分方程组的形式，不便于实际使用.摄动法适用于Stefan 数Ste很小的情况，在Ste较大时精度较差，因此这两种方法在实际使用时均有所限制[9].

准稳态法最早由Stefan 提出，并用于大潜热固液相变问题的近似求解[4].Crank[12]利用这一方法求解了直角坐标系下边界条件为∂T/∂x=C∂T/∂t（C为常数）的一维相变扩散问题，并推广到圆柱和球坐标下.Lin 等[13]利用直角坐标系下的Neumann 精确解对准稳态法进行修正，使其具有更高的精度，并将这一修正方法推广到柱坐标和球坐标恒壁温边界条件问题的求解.Megerlin 利用准稳态近似法求解了恒热流边界条件下直角坐标系下的熔化问题[4].Solomon[14]对Megerlin 的方法做出了改进，改进方法形式上与Goodman[15]提出的积分近似法一样，只不过不需要满足热平衡条件.上述的所有准稳态近似方法均是从数学角度出发来进行分析求解，通过假定一个简单形式的温度分布函数并让此函数满足边界条件和Stefan 界面条件，从而获得界面函数和温度分布的表达式.

总结而言，传统的准稳态近似方法实际上是完全忽略了相变材料显热的影响，在近似假设中只考虑相变潜热对传热过程的影响，这必然产生一定的误差.此外，针对圆柱坐标系中恒热流边界条件下的固液相变问题的准稳态近似求解目前还未见文献报道.本文将在准稳态近似方法的基础上，从热平衡角度出发推导给出一维平板和圆柱体外恒热流熔化问题的近似解，通过这种方法获得的近似解，比单纯利用准稳态法从数学角度推导出来的近似解具有更高的精度.

本文主要结构如下：首先，简单介绍了经典的一维平板恒壁温熔化问题，并给出适合工程计算用的熔化分数和无量纲换热拟合关系式.然后，定量分析了准稳态近似法的相对误差，并基于准稳态近似方法，从热平衡角度出发推导给出恒热流边界下熔化问题的无量纲关系式，并与其他近似解以及数值解进行对比.针对圆柱体外的熔化问题，本文给出了恒定热流下的改进型准稳态近似解，并与数值解进行对比，最后给出了适合工程计算使用的无量纲关系曲线图.

1 数学物理模型

1.1 直角坐标系

固液相变问题可分为凝固和熔化两类，其数学描述和求解过程是类似的，本文以熔化过程为例进行说明.根据固相区域是否存在温度梯度，熔化问题又可以分为单相熔化问题和两相熔化问题.熔化过程中主要的热量是以相变潜热的形式被吸收的，因此这里不考虑固相区域初始过冷的情形，而仅分析初始温度为相变温度的情况，也就是单相熔化问题.

在直角坐标系下，单相熔化问题也就是一维平板的熔化问题，其物理模型见图1(a）.初始时整个区域均处于初始温度Ti（Ti=Tm），Tm为相变温度.t＞0 时，边界x=0 处的温度突然升高到Tw（Tw＞Tm）或者给定恒定加热热流q′′，熔化过程随即开始，固液界面s(t)由左向右移动.由于固相区域始终处于相变温度，故不需要求解，这里仅对液相区域进行求解.如无特殊说明，下文中所有变量和参数均默认为是液相的.假定相变材料的物性参数保持为恒定值，该问题的数学描述如下.

图1 传导型固液相变物理模型：（a）平板单相熔化问题；（b）圆柱体外单相熔化问题Fig. 1 Schematics of single phase Stefan problems: (a) the semi-finite slab; (b) the cylinder

液相区域传热方程：

1.2 柱坐标系

类似地，这里结合图1(b）给出圆柱体外一维单相熔化问题的数学描述.

液相区域传热方程：

固液界面条件：

2 无量纲解析解

2.1 一维平板熔化问题

2.1.1 恒壁温边界条件

无量纲化是获得具有普适性关系式的重要方法，这里定义问题的主要无量纲参数如下：

其中，ε 为误差函数；λ 是熔化常数，由超越方程式（16）决定.由式（16）可以看出，熔化常数实际上仅仅是Ste的函数，这里将其定义为λ=f(Ste).

可以看出，对Stefan 问题的数学求解实际上只关心两个变量：界面函数S和温度分布θ.而在实际应用中，最直接关心的是熔化体积分数ϕ 和换热量.在直角坐标系下，熔化体积分数为

式（18）和（21）给出了表征一维平板单相熔化过程的最主要的无量纲关系式，现在的问题是如何获得f(Ste)和g(Ste)的表达式.由于f(Ste)=λ 是由超越方程式（16）决定的，理论上讲是无法获得其解析表达式的.而显式表达式显然是更便于实际使用的，特别是在参数化设计中.Carslaw 等[16]对误差函数ε(λ)的级数展开取一阶近似，得到了f(Ste)的近似表达式.然而，这一近似表达式仅对小的Ste（Ste＜0.1）成立，当Ste较大时，误差较大.因此，这里通过拟合关系式来获得f(Ste)和g(Ste)的表达式.

这里以设备热管理中常用的典型的石蜡相变材料n-eicosane[17-18]为例，可计算得其在50 ℃过热壁面温度下的Ste为0.47.对于低熔点金属相变材料，其Ste一般比同等温差下的石蜡小.对于大多数电子设备热管理问题，温差一般不会超过50 ℃.因此，可以认为在这一类问题中Ste≤0.5，这里仅在此范围内对f(Ste)和g(Ste)进行拟合.

图2 f(Ste)和g(Ste)拟合曲线Fig. 2 Fitting curves of f(Ste) and g(Ste)

此外，由式（18）和（21）可以得出，Nu与ϕ 的乘积仅仅是Ste的函数.图3 给出了Nu·ϕ-Ste变化曲线，可以看出Nu·ϕ≈1.且Ste越小时，Nu·ϕ 越小且越接近于1.这一结论实际上可以通过一个简单的假设得到.假定在液相区域内温度成线性分布，即θ=1-X/S(τ)，则

图3 Nu·ϕ 随Ste 的变化Fig. 3 Variation of Nu·ϕ with Ste

图4 给出了不同Ste下，熔化分数分别为0.2，0.5 和1 时的液相温度分布，并与线性化温度分布对比.可以看出，Ste越小，温度越趋近于线性分布.定量地说，在完全融化时刻，线性温度分布假设在Ste为0.5，0.3 和0.1 时的最大误差分别为5.7%，3.5%和1.2%.这是因为Ste是相变过程中，显热值与潜热值的相对大小的度量.Ste越小，说明显热相对于潜热而言越小，当小到显热可以忽略时，从壁面传递进来的热量几乎全部被相变材料潜热吸收，而被液相区域吸收的热量可以忽略，因此整个液相区域的温度梯度几乎是相等的，也就是线性温度分布.从数学的角度来讲，就是热扩散方程式（1）中左边的瞬态项可以忽略为0，也就是准稳态近似.

图4 线性化温度分布与精确值的对比Fig. 4 Comparison of approximation solutions and exact solutions

2.1.2 恒热流边界条件

上面提到的线性温度分布假设实际上就是传统的准稳态近似法的思想，针对恒定热流边界条件，对应的线性温度分布为

将式（31）代入式（29）可以得到

下面将定量对比这一改进的准稳态近似解与其他近似解的精度，包括Evans 等[6]给出的无穷级数解，这里取其前三项：

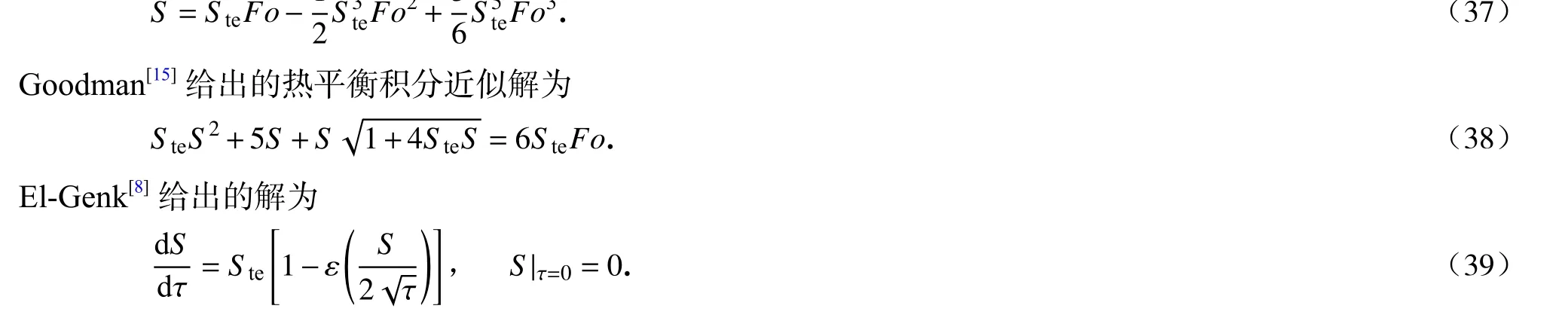
由于针对这一问题目前还没有公认的解析解，这里给出数值解作为参考.数值解由商业软件FLUENT 求解获得，数值算法采用经典的焓方法，并且忽略液相区域的自然对流.计算网格和时间步长的选择也经过了无关性验证.作为数值算法有效性的验证，图5 给出了恒壁温条件下平板单相融化问题的数值解（Ste=0.47），并与理论解做对比.可以看出两者吻合得非常好，说明数值解具有足够的精确度.下面所有的数值计算将采用同样的方法.

图5 恒壁温平板单相熔化问题数值解与精确解对比Fig. 5 Validation of the numerical method

图6 对比了几种不同近似解的精度，分别给出了Ste为0.1，0.3 和0.5 时固液界面位置S随无量纲时间Fo的变化曲线.以数值计算结果作为精确值的基准参考，定量对比不同近似解在S等于1 时对应的Fo数的大小相对于精度值的偏差，见表1.不难看出，Goodman[15]的积分近似解与数值计算结果吻合得最好，相对误差在1%以内.Evans 等[6]的级数解（取前三项）在Ste较大时，误差较大，达到-13.8%.El-Genk 等[8]给出的解在所有Ste情况下都与数值解偏离较多，在9% ～ 10%之间.传统的不考虑显热的准稳态近似解偏差也较大，在Ste从0.1 增加到0.5 时，其计算误差从-3.6%增加到-16.9%.本文提出的改进型准稳态结果与数值解吻合较好，其精度仅次于Goodman[15]的积分近似解，在Ste从0.1 增加到0.5 时，其计算误差在1.2% ～ 3.8%之间.与积分近似解（式（38））不同的是，本文给出的是界面函数关于Ste和Fo数的显式表达式，比隐式表达式使用起来更加方便.

图6 几种近似解与数值解的对比Fig. 6 Comparison of numerical results and approximation results

表1 几种近似解误差对比（以S=1 时的Fo 作为对比指标）Table 1 Comparison of different approximate solutions (Fo as the index for S=1)

2.2 圆柱体外熔化问题

2.2.1 恒壁温边界条件

对于圆柱体外的单相熔化问题，分析方法与前面基本一样.唯一不同的是，对于圆柱坐标，准稳态近似温度分布不再是线性分布，而是对数分布.这里，首先简单介绍圆柱体外恒壁温边界条件单相熔化问题的准稳态近似解.

针对圆柱体外恒壁温单相熔化问题（图1（b）），重新定义无量纲变量：

与式（41）不同的是，此时的壁面温度Tw(t)不再是常数，而是时间的函数，且满足边界条件：

图7 将式（48）与数值解进行对比，可以看出，改进型准稳态近似解与数值解十分接近，Ste越小，近似解与数值解的相对误差越小.由于式（48）是关于S的超越方程，无法获得解析解，这里以曲线图的形式给出其在不同Ste下随无量纲时间Fo数变化的曲线，以供实际计算参考，如图8.具体使用时，由外径内径比确定最大的Smax=γ，并在在图上画水平线，与相应的Ste的曲线相交，该交点对应的横坐标即为完全熔化时间，对应的曲线即为熔化曲线，如图7 中红色曲线（γ=2，Ste=0.3）对应的界面函数为图8 中的红色曲线部分.

图7 改进型准稳态近似解与数值解的对比Fig. 7 Comparison of the improved approximation solutions and numerical results

图8 改进型准稳态近似解Fig. 8 Improved quasi-steady-state approximation solutions

3 结 论

参考文献（ References ） ：

［1］ZHAO B C, LI T X, GAO J C, et al. Latent heat thermal storage using salt hydrates for distributed building heating: a multi-level scale-up research[J].Renewable and Sustainable Energy Reviews, 2020, 121（7）: 109712.

［2］ 李长玉, 方彦奎, 刘福旭, 等. 热防护服-空气-皮肤热传导模型及其解析解[J]. 应用数学和力学, 2021, 42（2）: 162-169.（LI Changyu, FANG Yankui, LIU Fuxu, et al. A thermal protective clothing-air-skin heat conduction model and its analytical solution[J].Applied Mathematics and Mechanics, 2021, 42（2）: 162-169.（in Chinese））

［3］FLEISCHER A S.Thermal Energy Storage Using Phase Change Materials: Fundamentals and Applications[M].Berlin: Springer, 2015.

［4］CRANK J.Free and Moving Boundary Problems[M]. Oxford: Clarendon Press, 1984.

［5］TAO L. On free boundary problems with arbitrary initial and flux conditions[J].Zeitschrift für Angewandte Mathematik und Physik(ZAMP), 1979, 30（3）: 416-426.

［6］EVANS G, ISAACSON I, MACDONALD J. Stefan-like problems[J].Quarterly of Applied Mathematics, 1950,8（3）: 312-319.

［7］SCHIAVONE P, CONSTANDA C, MIODUCHOWSKI A.Integral Methods in Science and Engineering[M].Berlin: Springer Science & Business Media, 2012.

［8］EL-GENK M S, CRONENBERG A W. Solidification in a semi-infinite region with boundary conditions of the second kind: an exact solution[J].Letters in Heat and Mass Transfer, 1979, 6（4）: 321-327.

［9］QU P, ZHANG C, LIAO X, et al. A new computation method for solidification process in a finite, initially overheated slab[J].Journal of Thermal Science, 1992, 1（4）: 272-277.

［10］BELI G E. Solidification of a liquid about a cylindrical pipe[J].International Journal of Heat and Mass Transfer, 1979, 22（12）: 1681-1686.

［11］YANG X H, LIU J. A novel method for determining the melting point, fusion latent heat, specific heat capacity and thermal conductivity of phase change materials[J].International Journal of Heat and Mass Transfer, 2018,127（Part B）: 457-468.

［12］CRANK J. Diffusion with rapid irreversible immobilization[J].Transactions of the Faraday Society, 1957, 53:1083-1091.

［13］LIN S, JIANG Z. An improved quasi-steady analysis for solving freezing problems in a plate, a cylinder and a sphere[J].Journal of Heat Transfer, 2003, 125（6）: 1123-1128.

［14］SOLOMON A D. The applicability and extendability of Megerlin’s method for solving parabolic free boundary problems[J].Moving Boundary Problems, 1977, 1: 187-202.

［15］GOODMAN T R. The heat-balance integral and its application to problems involving a change of phase[J].Journal of Fluids Engineering, 1958, 80（2）: 335-342.

［16］CARSLAW H S, JAEGER J C.Conduction of Heat in Solids[M]. Oxford: Oxford Clarendon Press, 1959.

［17］RUKH S, PASHA R A, NASIR M A. Heat transfer enhancement of round pin heat sinks usingn-eicosane as PCM: an experimental study[J].Heat and Mass Transfer, 2019, 55（2）: 309-325.

［18］ZENG Y, DONG J, KHODADADI J M. Thermal coupling-decoupling mechanism of heat transfer across van der Waals interfaces inn-eicosane[J].International Journal of Heat and Mass Transfer, 2021, 164（10）: 120603.