基于标准热阻的多类储热材料归一化动态表征及应用*

郝俊红， 邬学峰， 张师宁， 田 亮， 戈志华

（华北电力大学 能源动力与机械工程学院，北京 102206）

引 言

“双碳”战略的提出和新型电力系统的建设与快速发展，对各类储能方式都提出了新要求，如容量大、功率高、安全可靠、经济成本低等[1].其中，储热材料在太阳能热利用、光热发电、居民采暖、电网调峰、余热回收以及建筑节能等领域具有重要的研究和应用价值[2-3].然而，由于储热材料种类繁多，物性差异大，应用场景丰富，不同储热材料在储热、释热过程的外加激励不同，其动态响应也存在较大差异，与相关的传热介质和传热方式关系密切，如何快速高效地选配储热材料和换热工质，一直是学者们关注的研究重点.

目前，针对储热材料的动态特性，众多研究者采用数值模拟[4-8]、实验分析[9-10]和理论分析[11-14]等方法研究储热材料及不同结构的动态传热特性.如在数值模拟方面，Al-Sanea 等[4]通过有限体积法数值模拟研究墙体的动态传热特性以优化墙体绝缘层厚度；Kuravi 等[5]对热能存储系统的动态行为进行数值研究，以评估储热材料熔化的影响因素；Li 等[6]基于Modelica 语言对陶瓷材料的瞬态传热过程进行建模数值模拟，分析了材料储热、释热的动态特性.在实验分析方面，马令勇等[9]通过搭建实验平台对含有储热材料的屋顶进行研究，对比分析了材料不同物性参数对屋顶动态传热的影响；Pedersen[10]通过大量实验数据总结出水滴撞击热表面时的破裂速度与水滴状态对传热系数的影响.在理论分析方面，Artmann 等[11]利用一维热传导的解析解，量化了建筑结构的动态储热能力，以分析不同参数对结构动态储热能力的影响；Ozel[12]采用隐式有限差分法研究墙体内不同绝缘层位置的瞬态传热时间延迟与衰减因子，并优化了墙体分布.上述这些方法均能够较好地计算材料和结构的瞬态传热响应，但针对不同的应用场景，不能对不同类型的储热材料进行归一化的动态表征，并且储热系统与其他系统集成时，多维建模不利于跨系统的一体化整体分析.

另外，针对材料与结构的动态传热特性研究，已经有学者[15-16]明确了瞬态传热中的电容效应，并且Liu 等[17]通过比较瞬态电路中节点电流表达与非Fourier 传热中热流表达的相似性，为电路分析法运用于研究材料和结构的动态传热特性提供了理论依据.而能量流法的提出[18-19]，将储热材料的瞬态传热过程进行热电类比，构建的能量流模型可有效简化计算过程，使得储热过程与热系统能够有效结合[20-21].如He 等[22]和邵卫等[23]从能量守恒微分方程推导得出换热器的瞬态热量流模型，用于计算换热器的瞬态响应，并提出了时间常数用于表征换热器壁温对流体温度变化响应的快慢.Duan 等[24]和He 等[25]在计算单层和多层结构的瞬态传热时，对结构进行划分并引入节点温度，获得了单层及多层墙体和热防护的瞬态热量流模型，以计算结构的瞬态传热响应，得到时间常数表征结构的瞬态传热响应的快慢.杨婧等[26]构建了热网的热电比拟模型用于求解热网管道的瞬态响应，并推导得出了时间常数以表征管道出口温度随入口温度变化响应的快慢.由此可见，瞬态热量流模型可以很好地应用于材料和结构的瞬态传热计算中，并通过时间常数来表征材料的瞬态响应快慢.

本文从能量守恒微分方程出发，推导得出储热材料与流体换热过程中的瞬态换热热阻，获得储热材料与流体换热的瞬态热量流模型，提出以加热、储热、释热时间常数对储热材料瞬态传热达到稳态的快慢进行归一化协同表征，并开展数值模拟仿真，验证了所提出的基于多时间常数的归一化动态模型表征含义的准确性和可行性.最后，进一步提出该模型的使用场景，对多类传热、储热材料进行了对比分析.

1 储热材料的瞬态传热模型

对储热材料与流体的换热过程进行简化分析，假设储热材料在与流体换热时，热流体、冷流体分别从储热材料的上表面、下表面流过.图1 给出了二维视角下储热材料储热与释热时的换热示意图.热流体、冷流体通道的宽度分别为δh和δc，其进口温度分别为Th,i和Tc,i，热容率（比热容与质量流速的乘积）分别为Gh和Gc，热容分别为Ch和Cc，储热材料的厚度为δ，热容为Cs，其中间平面的平均温度为Tm.并建立以进口位置为y轴，冷热流体流动方向为x轴的坐标系.

图1 储热材料瞬态换热模型Fig. 1 The dynamic heat transfer model for heat storage materials

1.1 瞬态热量流模型的建立

参考文献[23]，从导热微分方程和能量守恒微分方程出发，对于一定厚度的储热材料，其内部传热热阻不可忽略，可以得到反映冷热流体与储热材料中间面之间换热关系的能量守恒微分方程：

式中Th，Tc分别为热流体和冷流体的温度，k为流体与壁面的对流传热系数，kh，kc分别为储热材料壁面与热侧流体和冷侧流体的传热系数，L为储热材料长度，λ 为材料自身的热导率，A为传热面积.式(1)描述了热流体中热量的变化，等式左侧第一项表示热流体中储存热量随时间变化的非稳态项，第二项表示因为流体与材料换热，流体沿流动方向上热量的变化，等式右侧表示流体与材料中间面的热量交换项.式(2)表示冷流体中的热量变化，其中每一项的物理含义均与式(1)相同.式(3)左侧表示材料中热量随时间变化的非稳态项，右侧第一项表示材料内部热量在x方向的传递，第二、三项分别表示材料中间面与冷热流体的热量交换项.

假设材料与流体交接界面传热系数均匀，材料内部温度在x方向上保持均匀，仅随时间变化，式(3)右侧第一项可以忽略.假设流体流量和热容率足够大，流体内热量随时间变化的非稳态项相比于流体沿流动方向热量的变化很小，忽略式(1)、(2)左边第一项.因此，式(1) ～ (3)可简化为

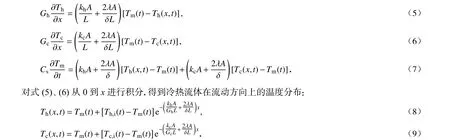
式(8)、(9)中Th,i(t)，Tc,i(t)分别为热流体和冷流体的进口温度，将Th(x,t)，Tc(x,t)代入式(7)中，并从0 到L进行积分，取平均值，得到储热材料中热量随时间的变化关系：

将冷热流体进口温度与材料中间面温度的传热温差作为驱动势，将传热温差与换热量之间的比值定义为传热热阻，那么式(10)可以改写为

结合热电类比理论，将温差类比为电路中的电势差，热阻类比为电阻，储热材料的热容类比为电路中的电容，可得到储热材料换热过程中的瞬态热量流模型如图2 所示.其中，热流体向储热材料传递的热量为Qh，材料向冷流体散热为Qc，其中Qh-Qc的热量储存到材料中.

图2 传热过程瞬态热流模型Fig. 2 The transient heat flow model for heat transfer process

类比节点电流方程，式(12)可以看作以中间面为节点的热量流方程，结合RC 电路中电容的零状态响应，对式(12)从0 到t进行积分，便可得到材料中间面温度随时间的变化关系：

类比电路响应中的时间常数，τ 为储热材料瞬态热量流模型的时间常数，表征传热达到稳态的快慢程度.储热材料的快慢程度不仅与储热材料的热容有关，还与冷热流体的对流传热能力及传热材料的导热能力有关.时间常数越小，储热材料越快达到稳态；时间常数越大，储热材料达到稳态越慢.

1.2 三阶电路瞬态热量流模型

为了更为准确地反映材料中间面温度在外加激励下的动态响应，参考文献[25]，引入节点温度Th,w，Tc,w，并经过对比验证采取文献中不同的划分方式，将材料平均划分为三份更能准确地反映材料中间表面温升.Th,w，Tc,w分别为热流体、冷流体与材料交接界面的节点温度，节点位置与材料内部发生热传导，与冷热流体发生对流换热，如图3 所示.增加节点方程个数，得到分层之后的能量守恒微分方程组：

图3 储热材料分层示意图Fig. 3 The layering diagram for the thermal storage materials

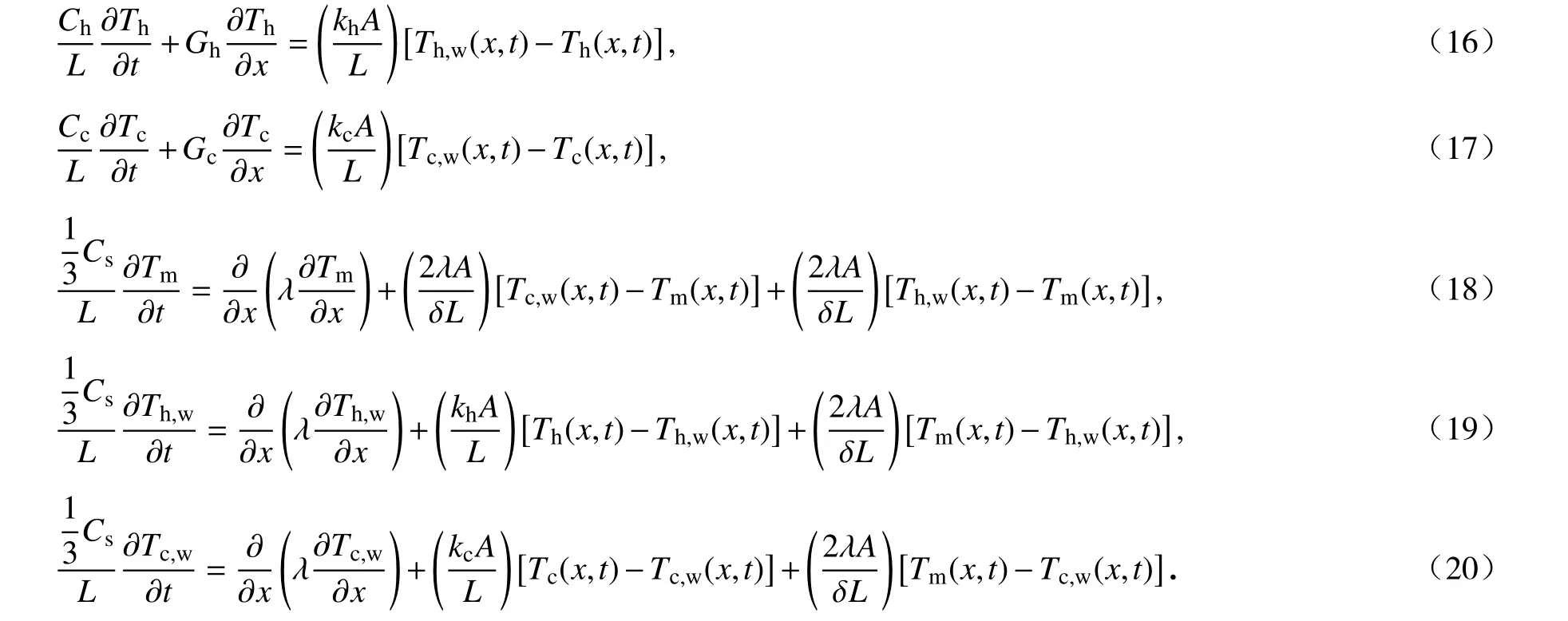
改写后的式(16)、(17)建立了冷热流体与节点之间的热量变化关系，式(18) ～ (20)表示每一控制容积的热量变化.

对引入节点后的微分方程组(16) ～ (20)采用上述的方法进行处理，仍以流体进口温度代替流体沿程平均温度，重新定义冷热流体与材料中心面的换热热阻，每一控制容积的热容都单独类比为一个电容，便可以得到三阶电路瞬态热量流模型的节点热量流方程组：

根据推导出的节点热量流方程组，可得到传热过程的三阶电路瞬态热量流模型，如图4 所示.继续对式(21) ～ (23)进行积分，便可得到三个节点温度随时间变化的关系式：

图4 三阶电路瞬态热流模型Fig. 4 The transient heat flow model for the 3rd-order circuit

由式(26) ～ (28)可以更精确地计算出材料中间面温度的响应变化.类比电路分析，三阶电路瞬态热量流模型得到的三类时间常数τh，τc，τm分别定义为加热、储热、释热时间常数，表征热流体向材料传热、材料内部传热、材料向冷流体传热的快慢，并协同表征整个传热过程到达稳态的快慢.从加热、释热时间常数τh，τc的表达式可以看出，不同类型的储热材料和换热流体组合时，会有不同的时间常数.针对动态换热能力，以时间常数为依据可以为储热材料选取适合的换热流体.储热时间常数τm只与材料的物性参数有关，说明中间控制容积达到稳态的快慢不受外界影响，可以用于分析材料自身的动态传热特性.上述三个时间常数针对不同的换热流体和储热材料，均可用来表示其瞬态传热过程，是一种归一化的动态表征方法.

2 模型验证及分析

为验证基于多时间常数的瞬态热量流模型，与有限元法计算结果进行对比.以图1 所示模型为例，流道参数恒定，流道宽度均为3 cm，为保证流体到材料处达到充分发展，流道长度设为50 cm，材料长度L为20 cm，为方便观察，初始温度均设为300 K.采用FLUENT 进行验证，网格采用Mesh 划分的结构化网格，流体出口采用压力出口边界条件，流体流动选择k-ε 标准湍流模型，算法选择Simple 算法.表1 给出了仿真验证设置，并将仿真计算所得换热系数代入瞬态热量流模型中，选取材料中间面平均温度作为参考温度进行对比.

表1 仿真验证设置Table 1 Simulation verification settings

图5 给出了不同流体与储热材料搭配时瞬态热量流模型计算结果与仿真计算结果的对比，其中，FLUENT、TEAM1、TEAM2 分别为使用FLUENT 有限单元法、一阶电路瞬态热量流模型、三阶电路瞬态热量流模型计算出的结果.可以看出，一阶电路瞬态热量流模型与仿真计算结果变化趋势相似，稳态温度也基本相同，但存在较大误差，三阶电路瞬态热量流模型计算结果无论在瞬态阶段还是稳态阶段，都能够更好地与仿真结果拟合.因此，运用三阶电路瞬态热量流模型计算储热材料的瞬态传热过程更为合理.

图5 瞬态热流模型与仿真结果对比：（a）仿真1；（b）仿真2；（c）仿真3Fig. 5 Comparison between transient heat flow models and simulation results: (a) simulation 1; (b) simulation 2; (c) simulation 3

从表2 中可以看出，不同储热材料与换热流体搭配时，计算所得时间常数存在明显差异.表2 与图5 结合来看，计算所得时间常数越大，达到稳态越慢；时间常数越小，达到稳态越快，以时间常数的大小可以简单反映储热材料与换热流体的动态传热与储热能力，三类时间常数可以协同表征瞬态传热达到稳态的快慢.

表2 时间常数Table 2 Time constants

针对材料厚度δ 均为10 cm 的氧化钙，冷侧流体流速为1 m/s、温度为300 K 的水，热侧流体速度为2 m/s、温度为350 K.当储热材料与冷侧流体保持不变，而热侧流体的类型发生变化时，表3 和图6 给出了加热时间常数和储热材料中心温度的变化.所得到的加热时间常数不同，并且材料中间面温升快慢也不同，其中case 3 的加热时间常数最小，传热过程最快达到稳态，case 2 的加热时间常数最大，达到稳态时间最慢，与换热流体的密度、比热和导热系数均有关系.由此可见，针对材料与流体的动态换热能力，以时间常数为标准，可以为储热材料与换热流体的选配提供依据.

表3 三种情况下热流体物理性质及加热时间常数Table 3 Physical properties and heating time constants of the thermal fluid in 3 cases

图6 三种情况下三阶电路瞬态热量流模型计算结果Fig. 6 Calculation results of the 3rd-order circuit transient heat flux model in 3 cases

瞬态热量流模型与仿真结果结合来看，不同参数的材料和流体搭配时，温度变化速率不同.热流体或冷流体的热容率、流速越大，加热或释热时间常数越小，材料内部温度变化越快.材料越厚、热导率越小，其内部传热热阻越大，材料储热时间常数越大，其内部温度变化越慢；材料的热容越大，所能存储的热量越多，三类时间常数均越大，材料内部温度变化越慢.通过计算得出三类时间常数，可以综合考虑流体与材料各类参数对储热系统动态换热能力的影响.

3 基于归一化动态模型的不同材料对比分析

上述提及的基于多时间常数的归一化动态表征模型能够用来反映储热材料与换热流体之间的储热与换热动态关系.本节将运用三阶电路瞬态热量流模型及时间常数，对多类不同储热材料与换热流体的组合进行对比分析.

3.1 高温流体与固体储热材料换热分析

太阳能热发电系统中需要高温流体与固体储热材料来实现高温储热和放热.如表4 所示的液态金属高温换热流体与表5 所示的固体储热材料.在对比分析中，采用了相同的换热与储热结构，换热流体通道宽度均为3 cm，材料长度L为20 cm，材料厚度δ 为10 cm.其中，热流体流速均为3 m/s，进口温度为773.15 K，材料的初始温度为300 K，冷侧流体保持一致，均为温度300 K、流速3 m/s 的水.其中流体与材料表面的换热系数由FLUENT 计算得出，具体物性参数如表4 和表5 所示.

表4 换热流体物性参数[27]Table 4 Physical parameters of heat exchanger fluids[27]

表5 储热材料物性参数[28]Table 5 Physical parameters of heat storage materials[28]

从表6 和图7 可以看出，只考虑流体与储热材料物性参数影响下的动态换热能力，液态金属与材料换热时能更快达到稳态.其中液态锂与硅质耐火砖、镁质耐火砖、钢筋混凝土换热时加热时间常数最小，液态钠与铸铁、铸钢换热时加热时间常数最小，HTS 熔融盐加热时间常数均最大.对于铸铁、铸钢高导热系数、大热容的材料，换热流体对换热达到稳态的快慢影响较小，对于同一材料不同换热流体的加热时间常数的差别在1 s以内，对于硅质耐火砖、镁质耐火砖、钢筋混凝土，换热流体对换热达到稳态的快慢影响有所增大，加热时间常数的差别在10 s 以内.可见，对换热达到稳态的速率影响主要来自于储热材料.

表6 加热时间常数(单位：s)Table 6 Heating time constants (unit: s)

图7 不同换热流体下储热材料中间面的温升：（a）硅质耐火砖；（b）镁质耐火砖；（c）钢筋混凝土；（d）铸铁；（e）铸钢Fig. 7 Temperature rises of intermediate surfaces of thermal storage materials in different heat exchange fluids: (a) silicon refractory bricks; (b) magnesia refractory bricks; (c) reinforced concrete; (d) cast iron; (e) cast steel

3.2 高温气体与陶瓷材料换热分析

陶瓷材料以其优秀的热传导能力和化学性质稳定的特点广泛应用于工业储热领域，储热陶瓷材料多为多孔结构，主要用于吸收高温气体的热量[29].下面简单以加热时间常数反映不同陶瓷材料在与高温气体换热时达到稳态的快慢，评价不同气体与陶瓷材料组合时的动态换热能力.陶瓷材料初始温度为300 K，物性参数由表7 给出，所选流体通道和材料尺寸与3.1 小节中保持一致，高温气体流速为3 m/s，进口温度为673.15 K，物性参数由表8 给出，低温气体保持空气不变，进口温度为300 K，流速为3 m/s.

表7 陶瓷储热材料物性参数[30]Table 7 Physical parameters of ceramic heat storage materials[30]

表8 高温气体物性参数[31]Table 8 Physical parameters of high temperature gases[31]

只考虑陶瓷材料的动态储热能力时，从表9 和图8 中可以看出，由于换热气体的物性参数差别较小，使得其对不同陶瓷材料的加热时间常数和温升状况影响差别不大，不同气体和同一陶瓷材料换热时的时间常数差别也在10 s 以内.相比较CO2和水蒸气，空气与不同种类陶瓷材料换热时，加热时间常数更小，能够更快达到稳态.由此可见，针对陶瓷材料的储热，在选择换热气体时可以优先选择空气.

表9 加热时间常数(单位：s)Table 9 Heating time constants (unit: s)

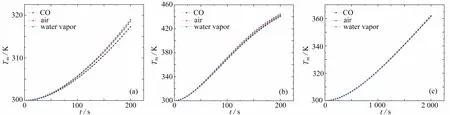
图8 不同换热流体下陶瓷材料中间面的温升：（a）石英；（b）碳化硅；（c）刚玉Fig. 8 Temperature rises of ceramic material intermediate surfaces under different heat exchange fluids: (a) quartz; (b) silicon carbide; (c) corundum

4 结 论

储热材料与换热流体的协同考虑及归一化动态表征是储热系统中材料快速选择与综合设计的关键基础.本文基于标准热阻模型和能量流法，从能量守恒微分方程出发，推导得出储热材料与流体的瞬态换热热阻，并得到储热-传热过程的一阶电路、三阶电路瞬态热量流模型，推导获得了加热、储热和释热三类时间常数，以此协同表征储热材料的动态响应特性.通过数值仿真计算，验证了瞬态热量流模型及时间常数表征含义的可行性和准确性.进一步基于多时间常数的归一化动态表征模型，对不同应用场景中储热材料与换热流体的适配性进行了对比分析.分析结果表明，当储热材料为硅质耐火砖、镁质耐火砖、钢筋混凝土时，流体选用液态锂可以更早达到稳态；而储热材料为铸铁、铸钢时，与液态钠换热能够更早达到稳态.高温工况下，对于石英、碳化硅、刚玉等储热材料，换热气体选用空气，换热达到稳态最快.总之，本文提出的归一化动态热量流模型可有效简化储热材料的瞬态传热计算，通过时间常数为储热材料与换热流体的选配提供了依据，为储热系统与其他系统的综合建模分析奠定了基础.

参考文献（ References ） ：

［1］ 陈海生, 李泓, 马文涛, 等. 2021年中国储能技术研究进展[J]. 储能科学与技术, 2021, 11（3）: 1052-1076. （CHEN Haisheng, LI Hong, MA Wentao, et al. Research progress of energy storage technology in China in 2021[J].Energy Storage Science and Technology, 2021, 11（3）: 1052-1076.（in Chinese））

［2］ 姜竹, 邹博杨, 丛琳, 等. 储热技术研究进展与展望[J]. 储能科学与技术, 2021, 38（5）: 1-26. （JIANG Zhu, ZOU Boyang, CONG Lin, et al. Recent progress and outlook of thermal energy storage technologies[J].Energy Storage Science and Technology, 2021, 38（5）: 1-26.（in Chinese））

［3］ 汪翔, 陈海生, 徐玉杰, 等. 储热技术研究进展与趋势[J]. 科学通报, 2017, 62（15）: 1602-1610. （WANG Xiang,CHEN Haisheng, XU Yujie, et al. Advances and prospects in thermal energy storage: a critical review[J].Chinese Science Bulletin, 2017, 62（15）: 1602-1610.（in Chinese））

［4］AL-SANEA S A, ZEDAN M F. Improving thermal performance of building walls by optimizing insulation layer distribution and thickness for same thermal mass[J].Applied Energy, 2011, 88（9）: 3113-3124.

［5］KURAVI S, TRAHAN J, RAHMAN M M, et al. Analysis of transient heat transfer in a thermal energy storage module[C]//Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition. Vancouver, Canada, 2010: 1251-1258.

［6］LI Q, BAI F, YANG B, et al. Dynamic simulations of a honeycomb ceramic thermal energy storage in a solar thermal power plant using air as the heat transfer fluid[J].Applied Thermal Engineering, 2018, 129: 636-645.

［7］TAHER N B, BOUKADIDA N, LAJIMI N. Thermal response of a composite building envelope under the climatic conditions of Tunisia[C]//Proceedings of the 2018 9th International Renewable Energy Congress（IREC）.Hammamet, Tunisia, 2018: 1-6.

［8］ 张荻, 郭帅, 谢永慧. 基于球窝结构冷却通道的强化传热数值及实验研究[J]. 应用数学和力学, 2014, 35（3）: 254-263.（ZHANG Di, GUO Shuai, XIE Yonghui. Numerical and experimental study of heat transfer enhancement based on the structure of cooling-channels with dimples[J].Applied Mathematics and Mechanics, 2014, 35（3）: 254-263.（in Chinese））

［9］ 马令勇, 朱永健, 郑雨蒙, 等. 含石蜡玻璃屋顶动态传热性能分析[J]. 热科学与技术, 2018, 17（6）: 444-448. （MA Lingyong, ZHU Yongjian, ZHENG Yumeng, et al. Analysis of dynamic heat transfer performance of glass roof containing paraffin[J].Journal of Thermal Science and Technology, 2018, 17（6）: 444-448.（in Chinese））

［10］PEDERSEN C. An experimental study of the dynamic behavior and heat transfer characteristics of water droplets impinging upon a heated surface[J].International Journal of Heat and Mass Transfer, 1970, 13（2）: 369-381.

［11］ARTMANN N, MANZ H, HEISELBERG P. Parametric study on the dynamic heat storage capacity of building elements[C]//Proceedings of the 28th AIVC Conference. Crete, Island, 2007 .

［12］OZEL M. Effect of insulation location on dynamic heat-transfer characteristics of building external walls and optimization of insulation thickness[J].Energy and Buildings, 2014, 72: 288-295.

［13］ 李长玉, 方彦奎, 刘福旭, 等. 热防护服-空气-皮肤热传导模型及其解析解[J]. 应用数学和力学, 2021, 42（2）: 162-169.（LI Changyu, FANG Yankui, LIU Fuxu, et al. A thermal protective clothing-air-skin heat conduction model and its analytical solution[J].Applied Mathematics and Mechanics, 2021, 42（2）: 162-169.（in Chinese））

［14］ 周保良, 李志远, 黄丹. 二维瞬态热传导的PDDO分析[J]. 应用数学和力学, 2022, 43（6）: 660-668. （ZHOU Baoliang,LI Zhiyuan, HUANG Dan. PDDO analysis of 2D transient heat conduction problems[J].Applied Mathematics and Mechanics, 2022, 43（6）: 660-668.（in Chinese））

［15］OLIVETI G, ARCURI N, MAZZEO D, et al. A new parameter for the dynamic analysis of building walls using the harmonic method[J].International Journal of Thermal Sciences, 2015, 88: 96-109.

［16］FRAISSE G, VIARDOT C, LAFABRIE O, et al. Development of a simplified and accurate building model based on electrical analogy[J].Energy and Buildings, 2002, 34（10）: 1017-1031.

［17］LIU Y, LI L, WANG J. A novel relation for heat flow using Maxwell thermoelectricity analogy[J].International Communications in Heat and Mass Transfer, 2020, 117: 104745.

［18］ 陈群, 郝俊红, 付荣桓, 等. 基于(火积 )理论的热系统分析和优化的能量流法[J]. 工程热物理学报, 2017, 38（7）: 1376-1383. （CHEN Qun, HAO Junhong, FU Ronghuan, et al. Entransy-based power flow method for analysis and optimization of thermal systems[J].Journal of Engineering Thermophysics, 2017, 38（7）: 1376-1383.（in Chinese））

［19］CHEN Q, HAO J H, ZHAO T. An alternative energy flow model for analysis and optimization of heat transfer systems[J].International Journal of Heat and Mass Transfer, 2017, 108: 712-720.

［20］CHEN Q, FU R H, XU Y C. Electrical circuit analogy for heat transfer analysis and optimization in heat exchanger networks[J].Applied Energy, 2015, 139: 81-92.

［21］ZHAO T, MIN Y, CHEN Q, et al. Electrical circuit analogy for analysis and optimization of absorption energy storage systems[J].Energy, 2016, 104: 171-183.

［22］HE K L, CHEN Q, LIU Y T, et al. A transient heat current model for dynamic performance analysis and optimal control of heat transfer system[J].International Journal of Heat and Mass Transfer, 2019, 145: 118767.

［23］ 邵卫, 陈群, 贺克伦, 等. 换热器动态特性分析的热量流模型[J]. 工程热物理学报, 2020, 41（11）: 2828-2833. （SHAO Wei, CHEN Qun, HE Kelun, et al. Heat current model for analying the dynamic characteristic of heat exchangers[J].Journal of Engineering Thermophysics, 2020, 41（11）: 2828-2833.（in Chinese））

［24］DUAN J, LI N, PENG J, et al. Full-response model of transient heat transfer of building walls using thermoelectric analogy method[J].Journal of Building Engineering, 2022, 46: 103717.

［25］HE K L, CHEN Q, DONG E F, et al. An improved unit circuit model for transient heat conduction performance analysis and optimization in multi-layer materials[J].Applied Thermal Engineering, 2018, 129: 1551-1562.

［26］ 杨婧, 唐岚, 赵开联, 等. 基于热电比拟模型的电热综合能源优化调度[J]. 电力科学与工程, 2022, 38（5）: 60-67.（YANG Jing, TANG Lan, ZHAO Kailian, et al. Optimization scheduling of integrated electric heating energy system based on thermoelectric analogy model[J].Electric Power Science and Engineering, 2022, 38（5）: 60-67.（in Chinese））

［27］ 谢刚. 熔融盐理论与应用[M]. 北京: 冶金工业出版社, 1998. （XIE Gang.Theory and Application of Molten Salt[M]. Beijing: Metallurgical Industry Press, 1998. （in Chinese））

［28］GEYER M.Thermal Storage for Solar Power Plants[M]. Springer, 1991: 199-214.

［29］ 任雪潭, 曾令可, 刘艳春, 等. 蓄热储能多孔陶瓷材料[J]. 陶瓷学报, 2006, 27（2）: 217-226. （REN Xuetan, ZENG Lingke, LIU Yanchun, et al. Porous ceramic materials for heat and energy storage[J].Journal of Ceramics, 2006,27（2）: 217-226.（in Chinese））

［30］ 李爱菊, 王毅, 张仁元, 等. 蓄热室新型蓄热体的研究进展[J]. 冶金能源, 2007, 36（1）: 43-48. （LI Aiju, WANG Yi,ZHANG Renyuan, et al. Research deveiopment of new type regenerative materials in regenerator chamber[J].Energy for Metallurgical Industry, 2007, 36（1）: 43-48.（in Chinese））

［31］ 陶文铨. 传热学[M]. 5版. 北京: 高等教育出版社, 2018. （TAO Wenquan.Heat Transfer[M]. 5th ed. Beijing: Higher Education Press, 2018. （in Chinese））