平衡阀节流区阀芯的温升及热变形分析*

王 恒,尚明明,徐义程,张 超,汪世益

(安徽工业大学 机械工程学院,安徽 马鞍山 243032)

0 引 言

目前,平衡阀已发展为集负载锁定、防压力冲击、抗空化及负载可控下放等多功能为一体的运动控制阀[1],在工程机械领域得到了广泛应用,是液压提升系统中的核心元件,其性能直接影响整个液压系统的性能。

平衡阀对液压系统的调节功能主要是通过调节节流口或者节流口组的流量来实现的。国内外众多学者对平衡阀的内部流场特性做了深入研究。

赵美卿等人[2]对螺纹插装式平衡阀进行了模拟仿真,结果发现,增大平衡阀的锥角角度可以减少其气蚀等现象的发生。刘兆领等人[3]对内缩型平衡阀进行了气穴与噪声数值仿真研究,得到了平衡阀噪声幅值的变化规律。冀宏等人[4]对几种典型的液压阀口过流面积进行了分析计算,其结果对液压复杂阀口的研究及设计计算具有一定的参考价值。兰秋华等人[5]采用计算流体力学(computational fluid dynamics,CFD),对滑阀的节流口进行了流量特性研究,提出了“流量数”(流量系数×过流面积)的概念。贺辉[6]设计了新型工程机械液压平衡阀,并将其与传统平衡阀进行了对比试验研究。陈波[7]对平衡阀进行了流场特性分析,得到了其阀口在不同条件下的流量系数变化,并推出了其流量系数随着压差和开度变化的一般规律。BEUNE A等人[8]采用流固耦合方法,研究了高压安全阀的开口特性,证明了在较高的设定压力下,只有入口压力快速上升才能迫使阀门打开;采用该方法可以评估安全阀的操作特性,以优化阀门设计。DENG J等人[9]研究了滑阀中,稳定的高速流体和凹口周围的局部温度分布,证明了黏性加热会导致其局部温度升高,从而引起阀芯的变形。

目前,众多学者对平衡阀进行了研究,但对平衡阀节流温升导致形变的问题研究较少。平衡阀的工作条件复杂多变,研究平衡阀的工作性能,温度是不可缺少的因素。

为此,笔者先建立平衡阀三维模型,并进行内部流场的有限元分析,研究平衡阀节流口处温度变化的特性以及阀芯变形的情况,为平衡阀的设计优化提供参考。

1 计算方法

笔者仿真求解流程为:首先,将建立的平衡阀三维模型导入ANSYS Workbench平台中,提取平衡阀主阀芯内部流体的三维模型,再对其进行网格划分;然后,将网格模型输入到Fluent软件中,选择合适的求解模型进行仿真;最后,把所得数据导入Static Structural中,进行结构求解,再对仿真结果进行可视化处理。

仿真求解流程的具体流程如图1所示。

图1 仿真研究的求解流程

2 平衡阀的工作原理及模型

2.1 工作原理

在提升系统工作过程中,有3种运动状态[10],即举重上升、承载静止和负载下行。

在承载静止过程中,要求闭锁性能好。上升工况时,重物的受力方向向下,重物的运动方向向上,此时,负载的作用是阻碍重物的运动,这样的负载称之为正负载;当重物下落工况时,重物的受力方向依然向下,但运动方向变成了向下,负载对运动起到促进作用,这样的负载称之为负负载。

而平衡阀主阀芯只在重物下落时,即负负载状态时开启,维持重物稳定下降,防止由重物加速下降而导致设备损坏和事故的发生。

2.2 仿真模型与几何参数

平衡阀的结构模型如图2所示。

图2 平衡阀结构模型

主阀芯的结构模型如图3所示。

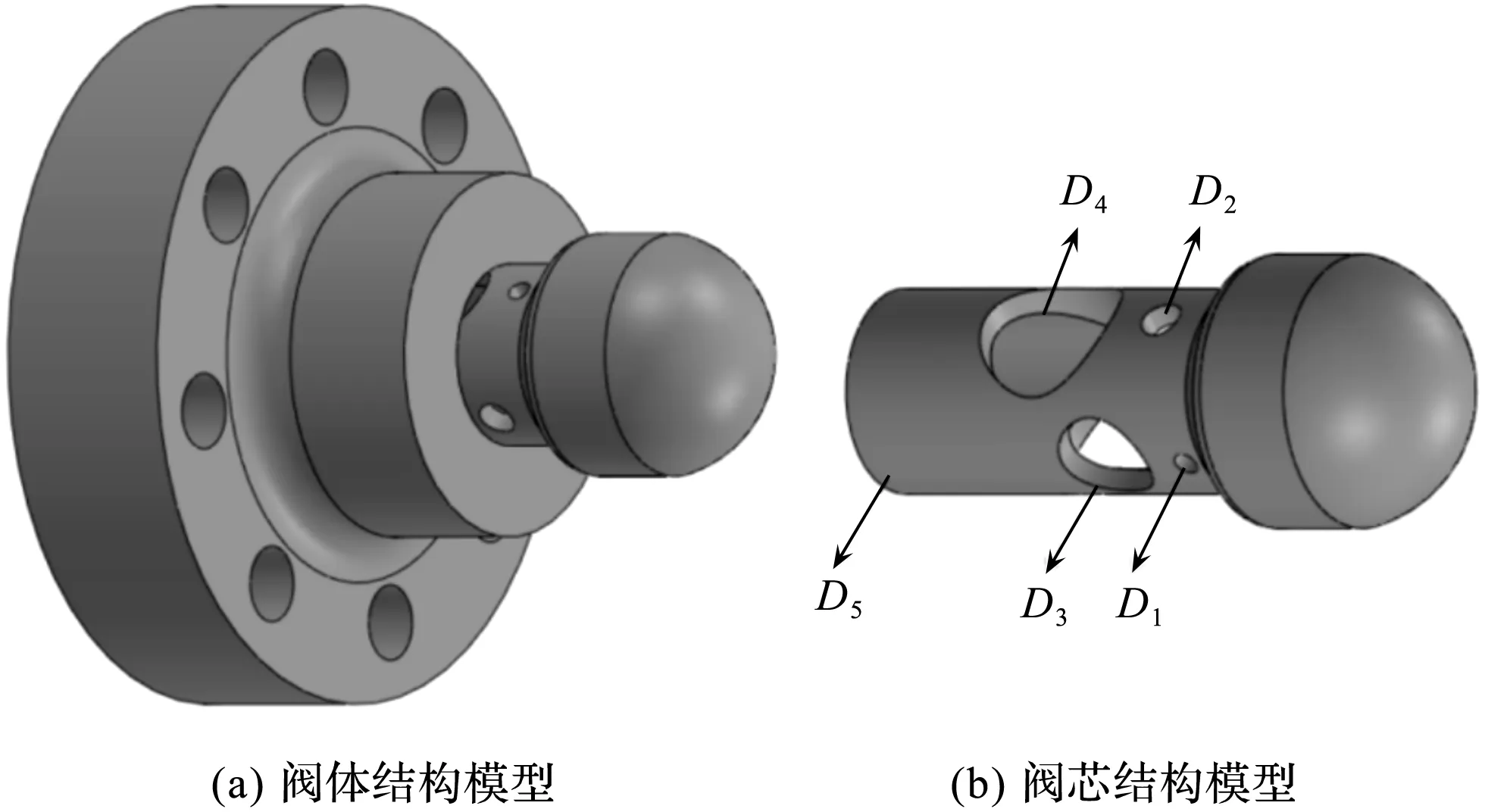
图3 主阀芯结构模型

图3中,平衡阀主阀为滑阀结构,主阀芯为圆柱类元件,阀口为多组圆孔沿圆周对称布置。

主阀芯的进口直径(内径)D5=4.55 mm,出口直径D4=4.5 mm,D3=3 mm,D2=1.25 mm,D1=0.75 mm。

3 流体控制方程及CFD仿真设置

随着计算机仿真技术的发展,计算流体力学(CFD)逐渐走向了成熟,可以满足对实际负载的流场进行求解分析。

目前，CFD被广泛应用于流体流场可视化分析领域,主要用于研究流体在液压阀、泵以及管道内随着不同的结构参数和边界条件变化的流场特性,以及液压阀的阀芯受力,与热结构耦合分析[11-14]。

3.1 控制方程

任何流体的流动都遵守质量守恒定律、动量守恒定律和能量守恒定律。

(1)质量守恒方程。

流体微元体在单位时间内的质量增加与同一时间内流入该微元体的流体净质量相等[15],其方程式为:

(1)

式中:ρ—流体密度;t—时间;u—速度矢量;u,v,w—分别为速度矢量在x、y和z方向的分量。

(2)动量守恒方程。

流体微元体的动量对时间的变化率与外界作用在该微元体上的合力相等[16],其方程式为:

(2)

(3)

(4)

(3)能量守恒方程。

当流动系统中包含有热交换时,流体流动遵守能量守恒定律。流体微元体中的能量增加率和力对该微元体所做的功与进入该微元体的净热流量之和相等[17],其方程式为:

(5)

该式的展开形式为:

(6)

式中:T—系统温度;kp—传热系数;cp—比热容;ST—黏性耗散。

3.2 CFD仿真设置

网格划分如图4所示。

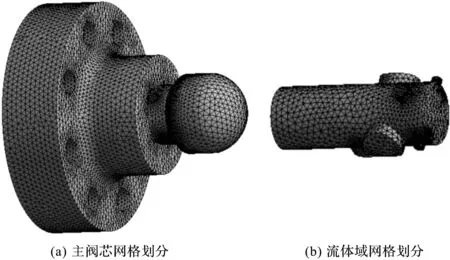
图4 网格划分

仿真边界条件:

(1)选择基于压力的稳态求解模式;

(2)流体介质选择液压油,密度:880 kg/m3,热导率:0.145 W/(m·K),动力黏度:0.035 5 kg/(m·s);

(3)介质为不可压缩的单相牛顿流体;

(4)忽略流体重力的影响;

(5)选择Realizable k-epsilon的湍流模型进行仿真计算,并激活黏性加热;

(6)固体材料为结构钢,密度:8 030 kg/m3,热导率:16.27 W/(m·K)。

4 仿真及结果分析

笔者对仿真结果进行可视化处理。可视化处理一般是对流场进行剖视切片。流场剖视选取的截面位置如图5所示。

图5 选取截面示意图

图5中,截面1为过Y-Z轴且平分阀芯的平面;截面2为过X-Y轴线且平分阀芯的平面。

仿真的工况参数如表1所示。

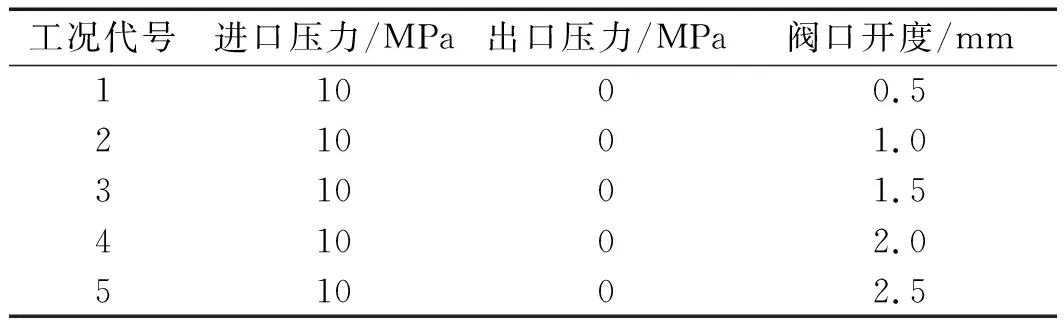
表1 仿真工况参数

4.1 速度场分析

截面1处的速度云图如图6所示。

图6 截面1处的速度云图

由于阀芯开度为1.0 mm时,截面1上的节流口流量较小,故该处笔者对其不予分析。

截面2处的速度云图,如图7所示。

由7图可知:节流口处流体流速最高,这是因为流体在流经节流口时,面积减小而导致速度增加;阀口开度为1.5 mm、2.0 mm时,可以观察到流体沿阀芯沟槽壁面形成涡形环流,且涡流只在截面2上产生,截面1未观察到涡流。

图7 截面2处的速度云图

4.2 温度场分析

流体温度分布云图,如图8所示。

由图8可知:温度升高的区域主要集中在节流口处,此时最高温度为368 K;远离节流口的区域温度变化不明显。这是因为流体在流经节流口时速度增加,与壁面产生摩擦,发生能量交换,以温度升高的形式表现出来。

图8 流体温度分布云图

进出口压差分别为:5 MPa、10 MPa、15 MPa、20 MPa时,阀口开度分别为:0.5 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm时,笔者对阀内流体温度的变化进行分析。

其中,最高温度随压差的变化曲线,如图9所示。

由图9可知:当进出口压差一定,开度不同时,流量不同,阀内流体温度也随之变化,在阀口开度为2.0 mm时为最高温度;随着主阀芯进出口压差的增大,阀内流体的温度也随着升高。这是因为压差增大,流体在节流口处的流速上升,所以更多的压力势能转化为动能。

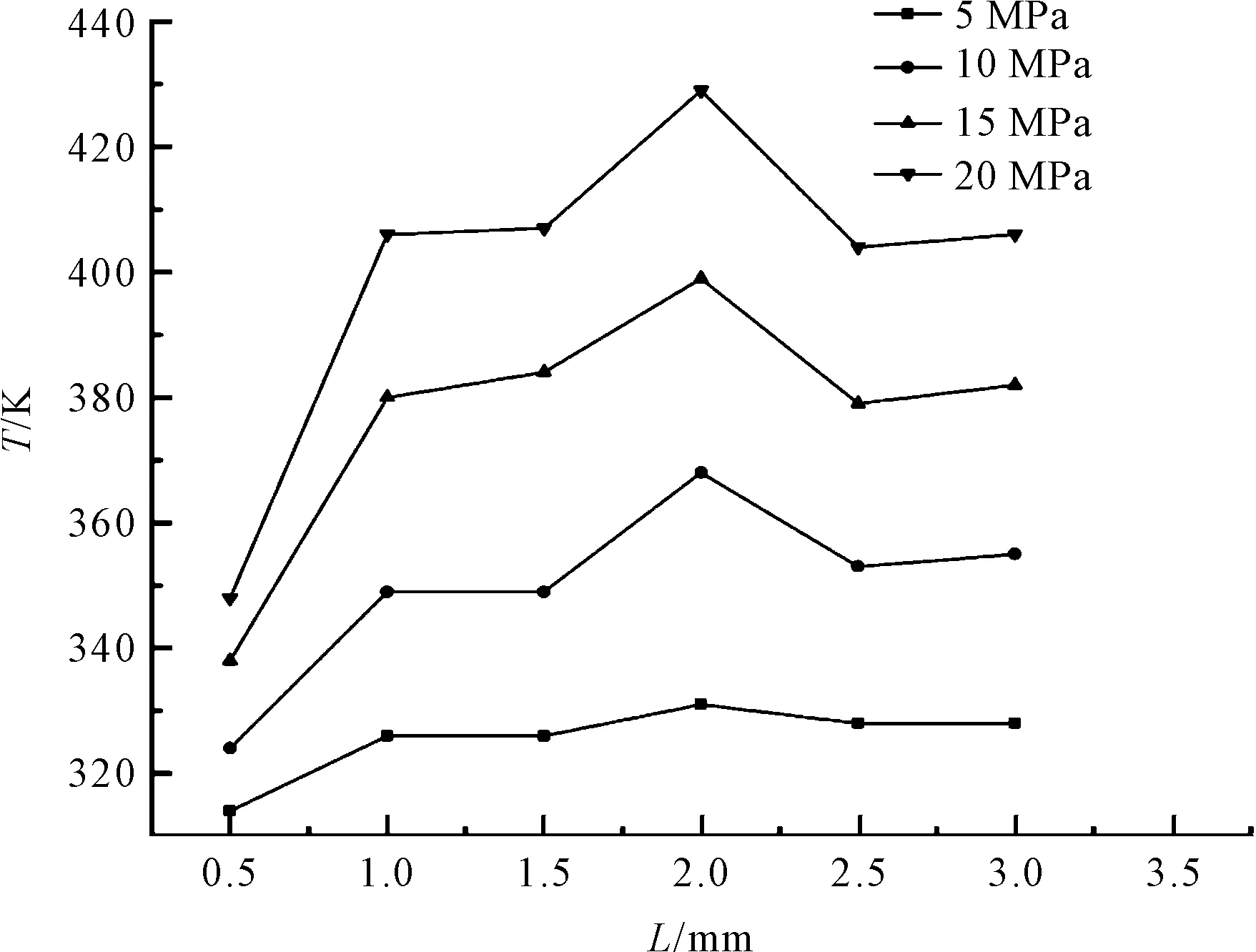
图9 不同压差和不同开度下阀内最高温度

4.3 阀芯的热变形

截面1处的阀芯变形云图,如图10所示。

图10 截面1处的阀芯变形云图

截面2处的阀芯变形云图,如图11所示。

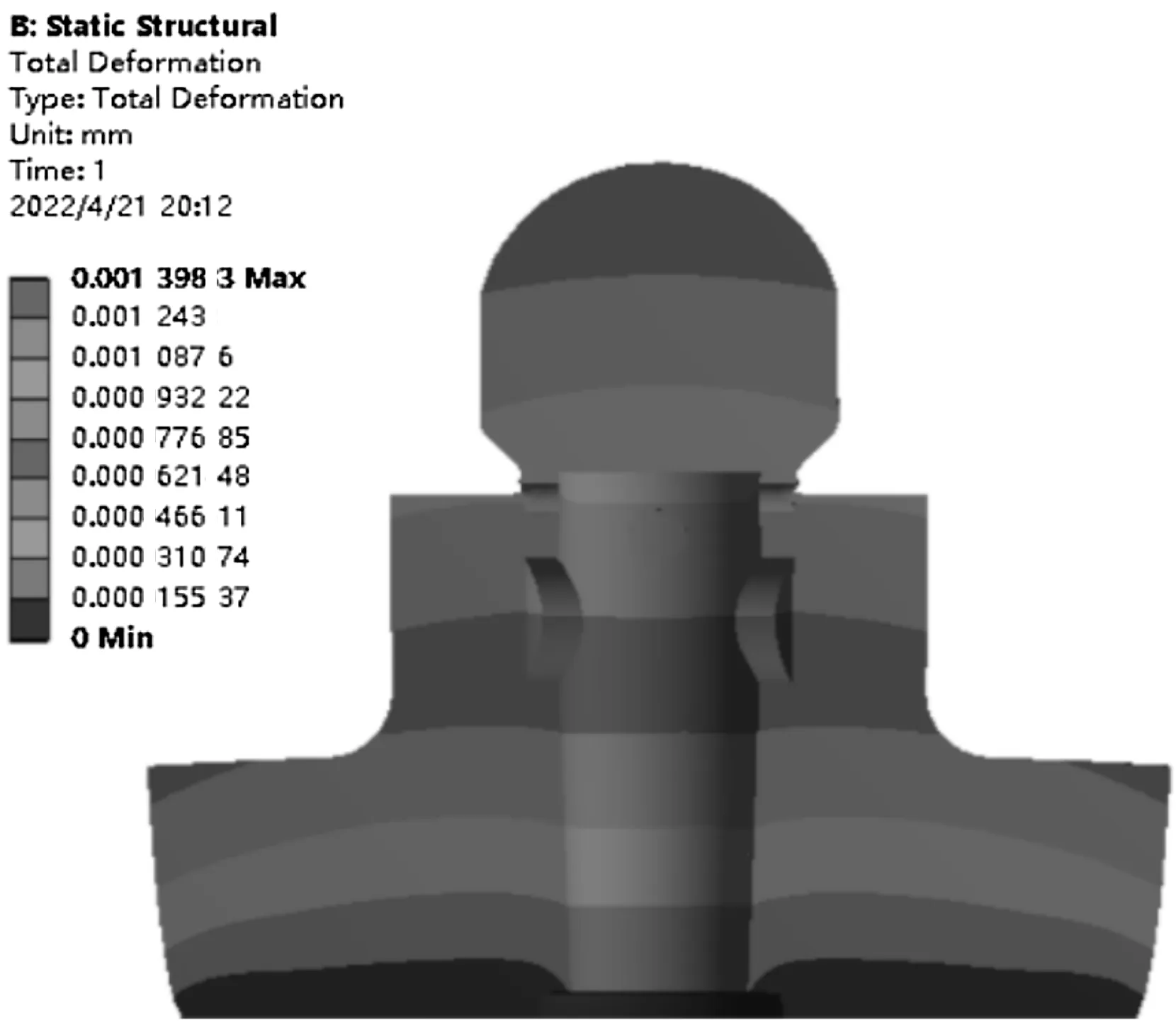
图11 截面2处的阀芯变形云图

不同开度下阀芯的最大形变量,如图12所示。

图12 不同开度下阀芯最大形变量

由图12可知:当阀芯进出口压差一定,在一定范围内,阀口开度增大时,流量随之增大,阀芯的最大形变量有所提升;阀芯在开度为2.0 mm时的形变量较大,这与图9的阀内流体温度变化相符,此时最大变形量为1.79。

仿真工况参数如表2所示。

表2 仿真工况参数

不同压差下阀芯的最大形变量,如图13所示。

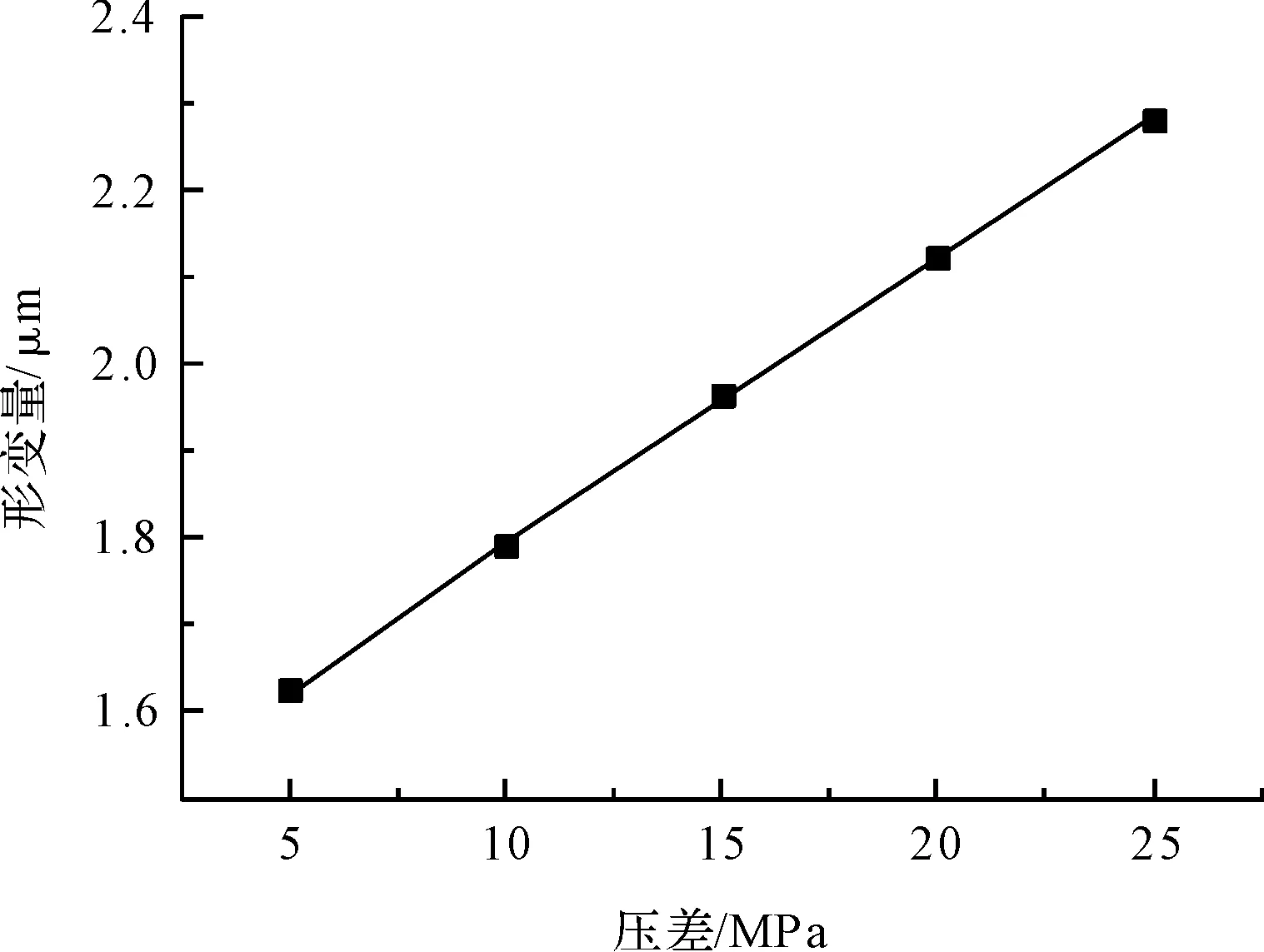
图13 不同压差下阀芯最大形变量

不同压差下,截面1处阀芯的变形云图如图14所示。

图14 截面1处的阀芯变形云图

不同压差下,截面2处阀芯的变形云图如图15所示。

由图15可知:当阀口开度一定,进出口压差增大时,流体的温度进一步升高,其压差在25 MPa时温度最高,此时阀芯的形变量较大,最大变形量为2.28,阀芯向四周隆起,在节流口处尤其明显,这将导致阀芯发生卡滞的现象。

图15 截面2处的阀芯变形云图

5 结束语

笔者首先采用SolidWorks建立了平衡阀的三维模型;然后,应用ICEM对平衡阀进行了网格划分;最后,应用ANSYS Workbench平台对平衡阀进行了不同工况下的模拟仿真。

研究结果表明:

(1)阀内流体存在温度分布不均匀。在节流口处温度较高,远离节流口处的温度变化并不明显,这是由于阀口处流体速度增加,与壁面摩擦产生能量交换,导致温度升高;

(2)节流口受温度影响会产生一定变形,在设计时应当注意温度对节流口的影响。阀口开度在1.5 mm～2.0 mm时,阀芯内流体容易产生涡流;

(3)受温度影响,阀芯会发生变形,局部直径变大,易导致阀芯发生卡滞的现象,设计时可适当放宽阀芯的尺寸公差;

(4)为了保证平衡阀的工作性能,阀芯变形应不超过2.0,笔者建议阀的进出口压差保持在15 MPa以内,尽量避免2.0 mm时的阀口开度。

在后续的工作中,笔者将进一步研究节流口形状及分布规律对主阀芯温升和形变的影响。