基于改进型前馈控制策略的多余力抑制方法*

王 斌,杨练根,聂 磊,马 雷,丁鹏飞

(湖北工业大学 机械工程学院,湖北 武汉 430068)

0 引 言

由于其控制精度高、反应速度快、传递功率大等优点,电液伺服系统在各种大型加载测试场合得到了广泛应用[1]。

比较典型的应用如电液伺服疲劳试验机,能够在实验室条件下模拟被测对象在实际工况中受到的外界交变载荷,检测出被测对象的各种性能参数。然而,电液伺服系统中含有大量的非线性环节,而且系统受到的外界干扰复杂多变,增加了控制系统的设计难度[2,3]。

在电液伺服加载测试试验中,位置扰动型施力系统是一种典型的测试方案,需要解决的关键问题在于如何抑制多余力的影响。所谓多余力指系统的加载力设定值为零时,且被测对象运动时,加载侧产生的力[4]。

针对多余力的抑制问题,国内外的学者做了很多相关方面的研究,大体分为两种:(1)结构补偿法。主要从加载系统的机械结构入手,通过增加辅助环节抑制多余力,如双阀并联[5]、安装连通孔、安装缓冲弹簧等;(2)控制补偿法。主要从控制策略入手,如模糊控制[6]、神经网络控制、滑模控制[7]、鲁棒控制[8,9]等。与结构补偿法相比,控制补偿法的成本低,无需改变设备的机械结构,能适应多种被测对象,是多余力抑制方法研究的重点。

基于结构不变性原理,潘卫东等人[10]采用主动位置同步控制法抑制多余力,该方法适用于位置干扰指令已知的情况,且其控制精度取决于两个系统控制特性的一致程度。段勇等人[11]采用随动位置同步控制法,利用快速傅里叶变换(FFT)分析被测对象运动的同时,使用最小二乘法修正补偿信号的相位;但该方法忽略了FFT的频谱泄漏问题,只适用于简单位置干扰的情况。余昱珩等人[12,13]提出了一种神经网络设计控制器,提高了加载系统的跟踪精度;但忽略了控制器模型对初始化参数选取敏感的问题。

上述文献中的方法虽然有效地抑制多余力,但对方法的使用条件有着较为严格的要求,因此,笔者提出一种可以适应未知复杂位置干扰的多余力抑制方法。

笔者以转向节台架试验机四轴电液加载系统为研究对象,在分析多余力产生的原因和建立单轴加载力与控制信号之间数学模型的基础上,提出一种包含谱序列变换FFT算法、补偿环节和双反向传播(BP)神经网络相位修正算法的改进型前馈控制策略,对多余力进行抑制。

1 系统分析与建模

1.1 四轴电液加载系统分析

转向节台架试验机的四轴电液加载系统如图1所示。

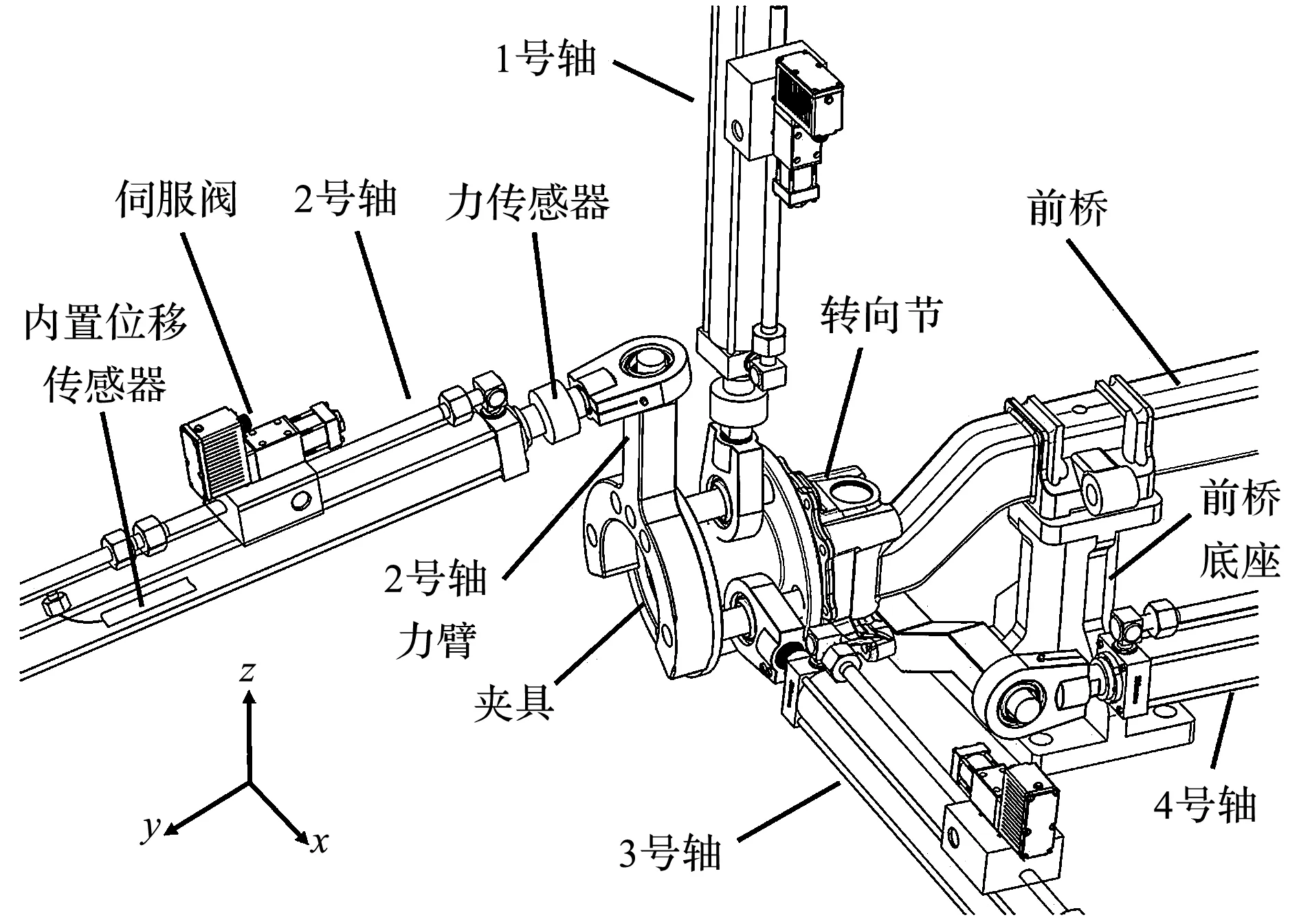
图1 转向节台架试验机四轴电液加载系统

由图1可知:前桥在Y方向上固定于底座之上,转向节连接在前桥的一端,通过夹具与各加载轴相连。在Z方向上的1号轴模拟加载垂向力,在Y方向上的2号轴模拟加载侧向力,在X方向上的3号轴模拟加载纵向力,调整在Y方向上的4号轴并固定转向节位置。

该设备可以通过更换前桥和夹具,实现对不同转向节的正弦加载测试。图1中,力传感器和位移传感器分别对当前加载力和活塞杆的位移进行检测。

由转向节台架试验机的结构可知,对垂向力进行正弦模拟加载时,转向节在YZ平面上产生以底座为圆心的往复圆弧运动,运动的幅度受加载力和前桥弹性系数的影响;该运动对2号轴产生Y方向上的位置干扰,导致2号轴液压油缸在运动时产生强迫流量,从而产生多余力。

因为转向节与夹具、夹具与各加载轴之间的连接存在间隙和摩擦,加上长时间疲劳测试产生的滑动、黏滞等非线性时变因素,所以由垂向力引起的位置干扰是由多个谐波和噪声组成的,干扰的基频与垂向力的加载频率相同。同理可得,模拟加载侧向力或纵向力时,会导致其他轴产生多余力。

由于各加载轴产生多余力的原因相同,所以该文以2号轴电液加载系统为研究对象,建立单轴加载力与控制信号之间的数学模型,对如何抑制多余力这一问题进行研究。

由上述分析可知:Y方向上的位置干扰是指2号轴力臂末端与2号油缸关节轴承连接点处的位移,可以由胡克定律计算得出:

F=kt(xa-ya)

(1)

式中:F—加载力;kt=3EtIt/L3,其中Et—力臂弹性系数;It—惯性矩;L—力臂长度,在力臂确定的条件下,kt为常数;xa—活塞杆位移;ya—Y方向位置干扰。

笔者在以下的研究中假设位置干扰已知。

1.2 单轴加载系统建模

笔者假设伺服阀是具有足够响应能力的理想四通滑阀,各节流窗口匹配对称,节流窗口处的流动为紊流,忽略液体的压缩性。

伺服阀流量线性化方程为[14]:

QL=kqxd-kcPL

(2)

式中:QL—负载流量;kq—伺服阀流量增益;xd—阀芯位移;kc—伺服阀流量-压力系数;PL—负载压力。

液压缸流量连续方程为:

(3)

式中:Ap—液压缸活塞面积;Vt—液压缸有效容积;β—等效容积弹性模量;cs—液压缸总泄漏系数。

力平衡方程为:

(4)

式中:mt—转向节及活塞杆折算到活塞上的总质量;Bc—活塞杆运动的黏性阻尼系数;Ff—活塞杆运动时所受到的摩擦力。

伺服阀阀芯位移方程为:

xd=ksvu

(5)

式中:ksv—伺服阀输入增益;u—伺服阀输入电压。

力传感器模型为:

(6)

式中:kf—力传感器系数;um—力传感器输出电压。

由式(2,3)可得:

(7)

式中:kce—伺服阀总流量压力系数,kce=kc+cs。

当单轴加载系统受到位置干扰的影响时,活塞杆具有一定的运动速度,而摩擦力Ff主要影响活塞杆低速运行时的加载精度[15,16],所以笔者忽略式(4)中的摩擦力,将式(1～7)进行拉氏变换,并整理、化简,得到单轴加载力和控制信号之间的数学模型。

单轴加载系统数学模型如图2所示。

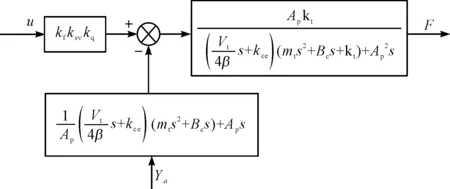
图2 单轴加载系统数学模型

2 改进型前馈控制策略

改进型前馈控制策略由谱序列变换的FFT算法、补偿环节和双BP神经网络相位修正算法3部分组成,其结构原理如图3所示。

图3 改进型前馈控制策略结构原理图

该前馈控制策略考虑到位置干扰运动状态的复杂性和传统FFT算法容易产生频谱泄漏的问题,应用谱序列变换的FFT算法精确分析位置干扰中的各谐波幅值与相位参数;在补偿环节利用谐波参数计算补偿信号的同时,双BP神经网络对补偿信号的相位进行修正,其中神经网络A对单轴加载系统进行辨识,获得雅克比(Jacobian)信息,神经网络B利用系统的误差信号和Jacobian信息对补偿环节的相位进行在线修正。

由系统分析可知:Y方向的位置干扰具有周期性,此时改进型前馈控制策略可以有效地抑制多余力;当位置干扰为非周期信号时,该策略对多余力的抑制效果有限,这主要是因为谱序列变换FFT算法对非周期信号分析的实时性较差,此时前馈控制无法及时抵消位置干扰对加载系统的影响。

2.1 谱序列变换的FFT算法与补偿环节

谱序列变换的FFT算法可以有效减少FFT算法的频谱泄漏误差,对谐波幅值和相位参数进行高精度检测[17]。

考虑到算法的复杂程度和谐波计算精度之间的平衡[18],笔者采用谱序列变换中的三点式算法对位置干扰进行分析,并将位置干扰表示为:

(8)

式中:M—谐波数量;Am—谐波幅值;fm—谐波频率;θm—谐波相位;N—FFT的采样点数;fs—采样频率。

根据结构不变性原理[19],由图2可得补偿环节Gf(s)为:

(9)

由式(8,9)可得相位修正之前的补偿环节输出为:

(10)

2.2 双BP神经网络相位修正算法

BP神经网络具有学习速度快、自适应性强等优点,可以逼近任意非线性函数,具有良好的泛化和自学习能力,被广泛地应用于各种非线性系统中[20]。

令BP神经网络A的输入层神经元为i(i=1,2,3…I),隐含层神经元为j(j=1,2,3…J),输出层神经元为d(d=1,2,3…D);隐含层和输出层的激活函数分别为tansig和logsig函数;选取样本学习总数P。

(11)

同理可得输出层神经元的输出为:

(12)

(13)

采用梯度下降法对权值和阈值进行调整:

w(kA+1)=w(kA)+Δw(kA)

(14)

c(kA+1)=c(kA)+Δc(kA)

(15)

式中:kA—神经网络A的学习次数;Δw—权值调整增量;Δc—阈值调整增量。

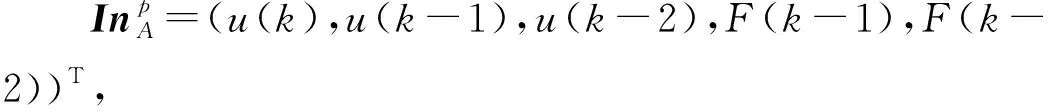
隐层神经元的数量影响神经网络的收敛速度和精度,因此笔者采用下式来确定其数量[21]:

(16)

式中:cB—隐含层节点数量;mB—输入层节点数量;nB—输出层节点数量;aB=6。

笔者根据式(16)确定隐含层的节点数量为9;令最大学习次数为500,学习速率为0.000 1,目标误差为0.001;网络的样本学习总数P=400,并对学习样本进行归一化处理,其中：kin1—控制电压u(k)的比例系数,ko—期望输出F(k)的比例系数。

BP神经网络A训练完成后,可得加载力和控制电压之间的Jacobian信息为:

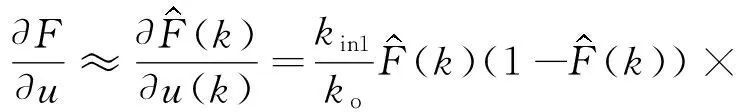
(17)

令BP神经网络B为在线学习模式,设输入层神经元为e(e=1,2,3…E),隐含层神经元为g(g=1,2,3…G),输出层神经元为q(q=1,2,3…Q);隐含层和输出层的激活函数分别为logsig和purelin函数。

神经网络B的前向传递过程与神经网络A类似,此处不再缀述。其反向传播过程如下：

因为补偿信号中含有多个谐波,所以笔者设补偿信号的整体时域移动tB为神经网络B的输出,根据式(10)可得相位修正之后的补偿环节输出为:

u1=

(18)

由于tB没有相应的期望输出,所以根据控制系统的设定值Fr和输出F,构建的损失函数为:

EB=0.5(Fr-F)2

(19)

第二层权值和阈值的调整过程如下:

(20)

(21)

(22)

(23)

式(20～23)中:η—学习速率;α—动量因子;kB—神经网络B的学习次数;u=u1+u2,u2—PID输出。

第一层权值和阈值的调整过程如下:

(24)

(25)

(26)

(27)

笔者采用上述BP神经网络B的算法修正补偿信号的相位[22]。

参数设置如下:由于实际补偿信号与理想值的相位差与位置干扰的频率有关[23],考虑到采样点数N对FFT运算时间的影响,选取神经网络的输入InB=(N/1 000,fm1,fm2,fm3,M)T,其中:fm1,fm2为两个最大的谐波频率;fm3为最小谐波频率。

选取隐含层的节点数量为9。学习速率η=1e-9,动量因子α=0.08,目标误差为0.1。

3 仿真分析

仿真过程中的单轴加载系统模型参数如表1所示。

表1 单轴加载系统模型参数

表1中,笔者通过实测力与力臂末端位移的数据后计算得出kt,该值与试验研究中转向节的额定载荷和夹具相对应。

根据系统分析可知,垂向正弦载荷引起的位置干扰是由多个谐波和噪声组成的,干扰的基频与垂向力的加载频率相同,所以笔者在进行仿真分析时,以低频和高频的正弦波以及噪声来模拟实际运行过程中的位置干扰。

Simulink单轴加载系统仿真模型如图4所示。

图4 单轴加载系统仿真模型

令位置干扰中白噪声的幅值为0.1 mm,当ya1=0.006sin(2πt)+0.000 3sin(16πt)时,多余力仿真结果如图5所示。

图5中,曲线1为PID控制下的多余力数据,曲线2为PID+传统前馈控制的多余力数据,曲线3为PID+改进型前馈控制的多余力数据。

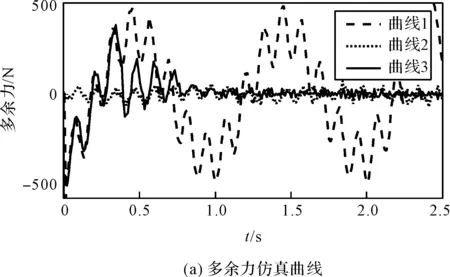
图5 位置干扰基频为1 Hz

当ya2=0.006sin(6πt)+0.000 3sin(16πt)时,多余力仿真结果如图6所示。

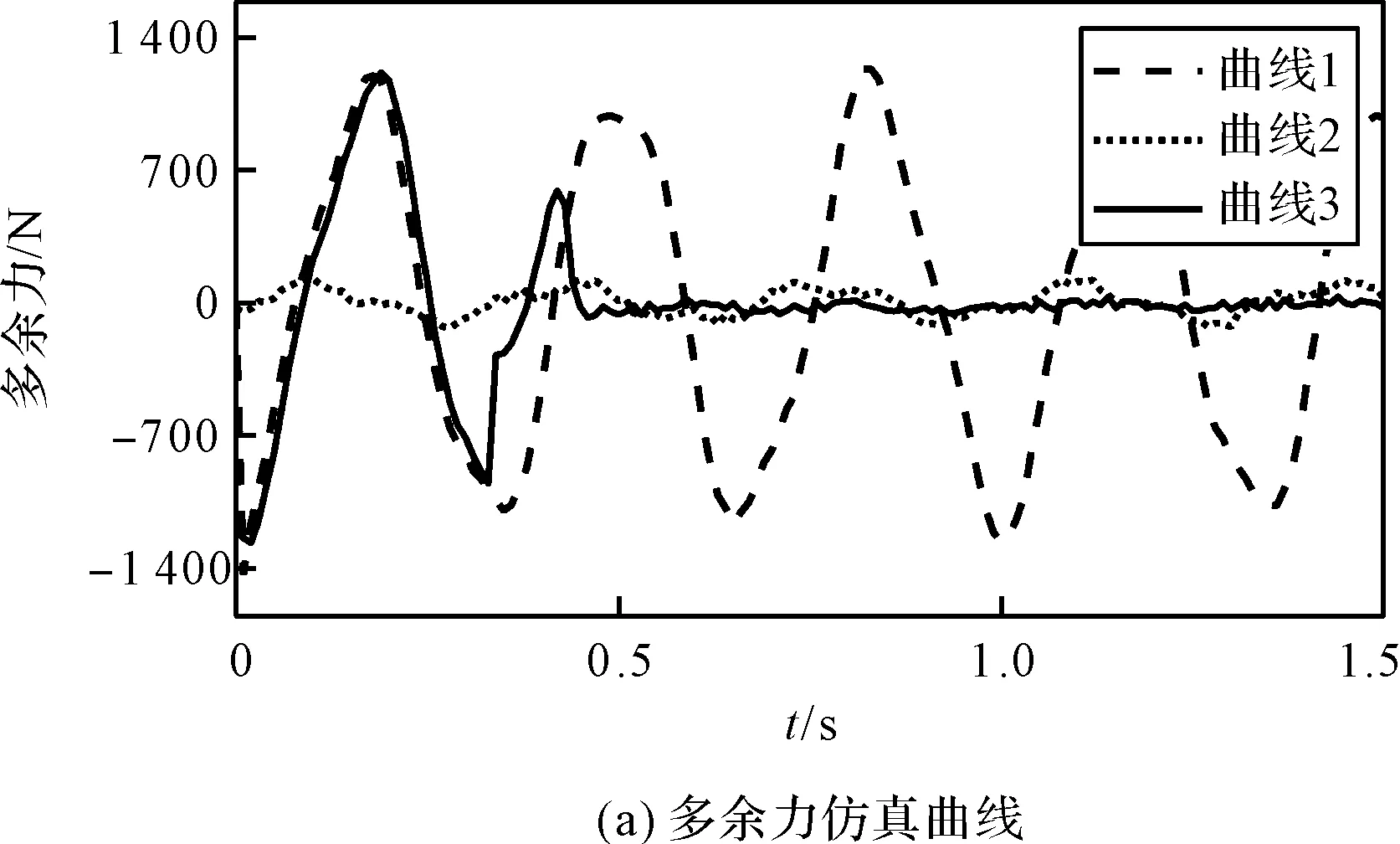
图6 位置干扰基频为3 Hz

当ya3=0.006sin(10πt)+0.000 3sin(16πt)时,多余力仿真结果如图7所示。

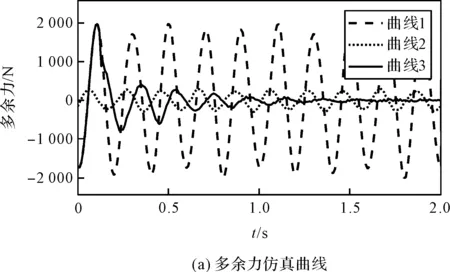
图7 位置干扰基频为5 Hz

由图(5～7)仿真结果可知:当位置干扰的基频分别为1 Hz、3 Hz和5 Hz时,BP神经网络B的时域输出最终收敛于1.004 6 s、1.004 4 s和0.804 4 s,改进型前馈控制对补偿信号中基频信号的相位修正为1.66°、4.76°和7.92°。除噪声干扰以外,仿真实验结果表明改进型前馈控制策略基本实现了对多余力的完全抑制,所以修正相位即不同频率位置干扰下的补偿信号滞后相位。

仿真结果表明:(1)随着位置干扰频率的增加,实际补偿信号与理想值的相位差越大,改进型前馈控制策略对多余力的抑制效果越明显;(2)该策略可以有效地抑制周期性正弦位置干扰引起的多余力。

4 试 验

此处,笔者试验研究所用到的转向节台架试验机实物图如图8所示。

图8 转向节台架试验机实物图

令1号轴加载力为0～50 kN,当加载频率为1 Hz时,2号轴的多余力试验结果如图9所示。

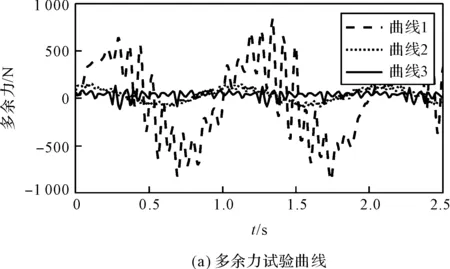
图9 1 Hz垂向力时2号轴多余力试验结果

当1号轴加载频率为3 Hz时,2号轴的多余力试验结果如图10所示。

图10 3 Hz垂向力时2号轴多余力试验结果

当1号轴加载频率为5 Hz时,2号轴的多余力试验结果如图11所示。

图11 5 Hz垂向力时2号轴多余力试验结果

由图(9～11)试验结果可知:当垂向加载频率为1 Hz、3 Hz和5 Hz时,BP神经网络B时域输出的变化范围分别为1.000 4 s～1.008 5 s、1.001 s～1.006 4 s、0.801 7 s～0.805 8 s,改进型前馈控制对补偿信号中基频信号的相位修正分别为0.14°～3.06°、1.09°～6.91°、3.06°～10.44°;

改进型前馈控制对补偿环节的相位修正是动态变化的,当修正相位大于零且小于2倍的滞后相位时,改进型前馈控制系统对多余力的抑制效果优于传统前馈控制。

对比仿真和试验结果可知:当垂向加载频率为1 Hz、3 Hz、5 Hz时,修正相位的变化范围与2倍滞后相位的比值分别为0.88、0.61、0.46,随着干扰频率的增加,修正相位的相对变化范围逐渐减小,改进型前馈控制策略对多余力的抑制效果越明显。

试验结果表明:与传统的前馈控制相比,改进型前馈控制策略能有效抑制高频阶段的多余力。

5 结束语

在分析多余力产生原因的基础上,通过建立单轴加载力与控制信号之间数学模型,笔者提出了一种包含谱序列变换的FFT算法、补偿环节和相位修正算法的改进型前馈控制策略,对多余力进行了抑制。

为了验证该策略的控制效果,笔者分别对PID反馈控制系统、PID+传统前馈控制的复合控制系统、PID+改进型前馈控制的复合控制系统施加了不同频率的含谐波与噪声的位置干扰。

研究结果表明:

(1)当位置干扰的频率为1 Hz、3 Hz、5 Hz时,补偿环节的相位滞后分别为1.66°、4.76°和7.92°;改进型前馈控制策略的动态相位修正范围与有效修正范围的比值分别为0.88、0.61和0.46;随着位置干扰频率的增加,补偿环节的相位滞后越大,改进型前馈控制策略对周期性位置干扰多余力的抑制效果越明显;

(2)虽然改进型前馈控制对低频阶段多余力的抑制效果与传统前馈控制基本相同,但有效地抑制了高频阶段的多余力。

在今后的研究中,笔者将采用自适应PID控制代替传统PID控制器,以进一步提高系统的动态性能和加载精度,减小低频阶段的多余力。