节制闸开度对侧渠分流量影响试验研究
李红,刘英,胡笑涛,陈土成,王文娥
(1.西北农林科技大学旱区农业工程教育部重点实验室,陕西杨凌 712100;2.北京市昌平区水务局,北京 102200)
0 引言
灌区渠系节制闸和分水闸是渠道水量分配和调度的重要建筑物[1-3],通过节制闸与分水闸配合实现分水口按量分流引水,其中主要通过节制闸的调控改变分水口处的水位满足灌溉引水流量,对渠道的输配水有着重要的影响,同时影响分水口及节制闸附近的泥沙分布[4-7]。因此,研究节制闸相对开度与水深、分水流量、流速分布的关系,对提高灌区流量监控、指导灌区水量分配及调控具有重要意义[7-9]。
节制闸结合分水口可具有分水和量水两种功能,目前大多研究集中于矩形渠道[10-12],主要通过不同的理论推导出一定使用范围内的流量计算公式或流量系数,如Hage[13]、Emiroglu[14]、刘海强[15]、王莹莹等[16]、徐祖信等[17]分别以动量定理、能量方程和无量纲分析原理为理论依据,认为流量系数是上游傅汝德数、堰长与河道宽度、堰长与水流深度、堰高与水流深度之比的函数,建立了考虑各种尺寸参数的矩形侧堰流量系数方程,推导出形式简洁的分流流量公式,并用试验数据验证[18]。郑国华等[19]、宋禹德等[20]探讨了渠道分水的问题,给出了利用主渠上游稳定水位计算侧渠道流量系数的计算公式,较好的实现渠道流量测控一体化。Taylor[21]、Keshavarzi[22]根据试验结果,明确了主渠和侧渠上下游水深与分流比之间的关系,并且发现流量系数与上游傅汝德数、侧堰高度和渠道底坡的有着一定的关系。已有研究主要通过试验及模拟等方法对不同渠道结构下的流量公式的影响因素进行研究[23,24],发现局部水头损失系数随相对闸门开度的增大而减小[25,26],堰流流量及流量系数与堰顶水头存在函数关系[27],且在自由出流的条件下,流量系数取0.36~0.375之间最适宜,并已有的流量公式进行补充修正[28,29]。Salmasi[30]用多元非线性回归法预测了不同闸门几何形状下的闸门流量系数,得出闸门几何形状对流量系数有较大影响。秦晨光[31]基于传统的流量公式形态利用回归方法得到了流量系数的计算公式,并指出该分段函数在自由出流条件下有良好的应用效果。候冬梅[32]认为传统的堰流和闸孔出流的判别e/h=0.65 仅适用于自由出流的条件下,因此针对特定条件下堰闸流量计算方法进行数据拟合,得到适用于调水工程中流量计算公式。目前梯形渠道节制闸调节分水口水位及分流量的影响研究较少[33]。
梯形渠道是我国灌区最常见的渠道类型,通过梯形渠道节制闸不同开度下分水口水流特性及分流规律试验研究,基于量纲分析,分析闸孔出流与堰流的闸门相对开度阈值,确定分流流量系数与影响因素之间的关系,建立节制闸调控侧渠分流量的表达式,为节制闸调控渠系水位流量提供理论依据。
1 材料与方法
1.1 试验系统布置
试验在西北农林科技大学旱区农业工程教育部重点实验室进行,试验系统由蓄水池、泵、梯形渠道(主渠)、矩形侧渠、节制闸及直角三角形薄壁堰(两个)和回水渠道构成。节制闸为矩形平板闸门,宽30 cm,与梯形主渠底宽相同,闸门两侧设置两块三角形闸墩,与梯形渠道侧壁之间封闭。试验布置如图1所示。
试验梯形主渠长30 m、底宽0.3 m、深0.6 m、边坡系数为1.0。在距主渠渠首20 m 处为一矩形分水渠即侧渠,长为7 m,宽和深为0.6 m,主渠与侧渠成90°夹角,侧渠底部高程高于主渠7 cm。主渠道共设15个断面,即断面1~15(图1)。在距离分水口上游90 cm 处布设断面1,分水口下游265 cm 处布设断面15,各断面分别选取1个测点量测主渠节制闸前后的稳定水深。为了更详细分析分水口和节制闸前后水深变化规律,在分水口上游布设两个断面2 和3,分别距离分水口40 和20 cm,每个断面布设3个测点;在分水口处布设4个断面,即断面4~7,各断面间距均为20 cm,由于分水口处水流流线变化较大,所以每个断面布设7 个测点;分水口与节制闸之间布设4 个断面(8~11),断面8距离分水口断面7的间距为15 cm,各断面间距为25 cm;节制闸下游布设3 个断面(12~14),断面12 距离节制闸的间距为15 cm,各断面间距为25 cm。a轴线表示主渠道靠近分水口一侧,b轴线表示主渠道中轴线,c轴线无分水口一侧,断面和测点的具体布置如图1(b)所示。直角三角薄壁堰流量Q采用Q=1.343H2.47计算(Q为流量,m3/s;H为堰上水头,m);水深采用SCM60型水位测针测定,精度为±0.1 mm。

图1 试验系统及断面测点布置图Fig.1 Layout of the test system and section measurement points
试验设置了5 种主渠来流量(Q=25.35、28.93、32.38、35.50、39.70 L/s),每个来流量下调节5~7个闸门开度e,以e=1 cm 为起始值,2 cm 为一个间隔,为了确定闸门出现临界状态(孔堰流的临界状态)的开度,部分来流量下(35.5 L/s)闸门开度间距设置为1 cm。共31 组试验工况,表1 是试验条件和组次。各工况下分别测定16 个断面的58 个测点的水深,主渠来流量Q及分流量Q2由主渠上游和侧渠下游的直角三角堰测得。试验中发现靠近闸门和分水口处渠道横断面的水面有波动,断面不同位置处水深存在一定差异,断面10 的水面较平稳,因此采用该断面的水深作为闸前稳定水深h。

表1 试验条件和组次Tab.1 Test conditions and groups
2 基于量纲和谐原理的分流量计算
量纲和谐原理可以对所拟合的公式进行检验,从量纲的规律性出发推求物理量之间的函数,确定物体运动规律。量纲分析法一般分为瑞利法和π定理两种,其中π定理较为普遍。本文采用π定理推求在节制闸调控过程中矩形侧渠分流量公式。影响侧渠流量Q2的因素包括主渠道底宽B、侧渠宽度b、闸前水深h、闸门开度e、液体密度ρ、重力加速度g以及动力黏滞系数μ和表面张力系数σ等,由于试验中,渠道闸前水深超过10 cm,表面张力影响很小;雷诺数Re为3.82×105~7.39×105,渠道内的流道是充分发展的紊流,黏滞效应相比重力效应,对水流影响较小,因此动力黏度μ和表面张力σ可忽略不计[20]。主渠底宽、侧渠宽度、水的密度及渠道粗糙系数均不变,可得关系式:

式中:Q2为侧渠流量,m3/s;h为闸前稳定水深,根据试验观测断面10水深稳定,可作为分流量计算的水深测流断面m;e为闸门开m;υ为主渠流速,m/s;g为重力加速度,m/s2。选取h和g作为基本物理量,其余变量可用基本变量表示,式(1)可变为:


3 结果分析
3.1 水面线
水面线沿程变化可直观反映渠道内水流流态变化规律,节制闸开度变化使分水口附近水深发生变化。由于5种来流量下水面线变化趋势大体一致,因此,图2给出了3种主渠来流量(Q=39.70、32.38、25.35 L/s)和多种闸门开度下主渠道中剖面(b轴线)沿程水面线变化规律。
从图2可以看出,闸孔出流时,主渠道水面线在分水口附近呈现先降低后升高的趋势,不同流量下水面线变化趋势一致,水深最小值的位置在分水口上游段处,最大值的位置在分水口下游段处。这是由于一部分水流进入侧渠使靠近分水口上游段水位下降,另一部分水流由于扩散受边壁影响而产生横向流速,且受到下游闸门阻力的影响,产生回流,与来流汇合碰撞,使分水口下游端水位壅高。由图2可知,同一主渠来流量下,闸门开度在一定范围时水流从闸门底部流出,在闸后形成收缩断面;随着闸门开度的增加,闸前水位逐渐下降,最后水流脱离闸门控制,形成堰流;自由出流条件下,流量不同时,形成堰流的临界闸门开度不同,流量为25.35、28.93、32.38、35.50、39.70 L/s时,临界闸门开度e分别为11、11.6、12、13、14 cm,闸门相对开度e/h(闸门开度与闸前稳定水深之比)分别为0.792、0.798、0.808,0.819 和0.823。理论上,当闸底坎为平底时,闸孔出流和堰流转换的临界闸孔相对开度e/h为0.65[34],但张敬楼、邱勇、袁新明等人[35-37]对闸孔出流和堰流界限研究发现,堰流和闸孔出流的阈值并非定值,该阈值受闸门形式与布设位置、主渠来流及上下游水流流态等影响,存在一定变化范围。本试验中,梯形渠道平板节制闸堰流和闸孔出流的相对闸门开度阈值在0.792~0.823之间,随主渠来流量的增大而增大。其原因是本研究中闸墩突然束窄过流断面,形成侧收缩,过闸水流受其影响,闸前水面不是水平面,靠近闸门中间位置水面最低,向两侧水面逐渐升高;图3给出了闸孔出流堰流时,节制闸上游一定范围自由水面形状示意图,当相对闸门开度为0.65 时,闸门中间位置的水流已脱离闸门下缘,但两侧还受闸门限制,继续加大闸门开度才能使过闸水流完全脱离闸门下缘,形成堰流,所以相对闸门开度阈值大于理论值。

图2 主渠道沿程水深变化规律Fig.2 Variation law of water depth along main channel

图3 节制闸上游一定范围自由水面形状Fig.3 The shape of the free water surface in the range of 50 cm upstream
3.2 傅汝德数对流量系数的影响
弗劳德数Fr是反映明渠水流流态的一个重要参数,节制闸启闭过程中对分水口水流流态产生扰动,进而影响侧渠过流量。弗劳德数Fr采用下式计算[32]:


由式(4)可知,侧渠分流量的流量系数m与断面10 的弗劳德数Fr有关,需进一步探究Fr的变化对m的影响。图4为不同流量下断面10的弗劳德数Fr与流量系数m关系曲线,由图4可知,断面10 的弗劳德数最大值为0.413,小于0.5,说明该断面处水流流态较稳,满足水位测点的要求。不同主渠来流量时,流量系数随弗劳德数的增大而减小,这是因为随着闸门开度增大,主渠流速变大,导致弗劳德数增大,使主渠水流惯性力增大,侧渠分流能力减弱,进而影响流量系数变小。且主渠来流量越大,流量系数降幅越大,Q=39.7 L/s 时最大降幅为10.50%,说明大流量工况较小流量对流量系数的影响更加明显,即大流量工况下闸门开度越小主渠道水深越深,侧渠分流流量越多,所以流量系数比较大。由此可见,相对闸门开度对流量系数的影响大于弗劳德数对流量系数的影响。
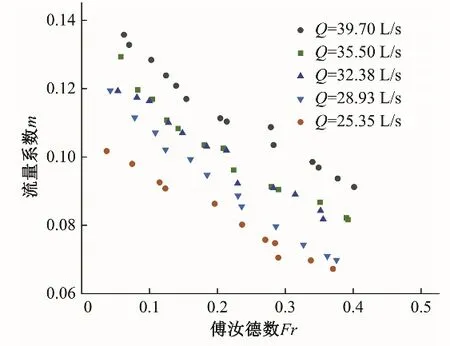
图4 断面10傅汝德数Fr与流量系数m关系Fig.4 Relation between Fr and flow coefficient m in section 10
3.3 闸门相对开度对流量系数的影响
调节节制闸可以控制分水口处的水位,达到按量配水的要求。由式(4)可知,侧渠分流量的流量系数也与闸门相对开度有关。图5给出了相对闸门开度e/h与流量系数m的关系,从图中可以看出,来流量一定时,随着闸门开度的增大,主渠过闸流量增大,侧渠分流量减小,侧渠流量系数也随之减小;某一流量下,流量系数m与闸孔相对开度e/h的增大而线性减小,可通过无量纲数e/h确定矩形支渠流量系数,得到侧渠流量的大小。

图5 相对闸门开度e/h与流量系数m的关系Fig.5 Relation between e/h and flow coefficient m
通过线性拟合可以得到不同流量下流量系数m与e/h的关系式,如表2 所示。各关系式相关系数达到0.938 以上,精度较高。相对误差均小于6.5%。表2 可以看出,各流量下流量系数与相对闸门开度的公式中,流量系数的斜率随来流量的增加而减小。

表2 不同来流量下侧渠流量系数m与相对闸门开度e/h关系式Tab.2 Relationship between flow coefficient m of the diversion channel under different flows and relative gate opening e/h
通过试验可知,主渠来流量与上游稳定水位之间存在一定关系,图6 给出不同流量下上游稳定水深和闸前水深之间的关系,通过SPSS 软件拟合,得到流量系数与闸门开度和闸前水深的关系式:

图6 上游稳定水深和闸前水深Fig.6 Upstream water depth and gate front water dept

其中,Q∈[25.35 L/s,39.70 L/s],e∈[0,14],e/h∈[0,0.823]。
图7 为上式计算值与实测值的分析对比,数据点均匀落在1∶1附近,表明计算值与实测值吻合,平均误差为0.75%,计算公式精度较好,将式(10)代入式(4),即可求得分流量。

图7 实测值与计算值对比Fig.7 Comparison of simulated and measured values
3.4 分流比
分流比作为渠道分水的重要因素,在分水过程中通过调节闸门开度使闸前和分水口处水位壅高来改变分流比,以达到改变侧渠流量的目的。因此,相对闸门的影响不可忽略,图8所示不同来流量下相对闸门开度与分流比的关系。由图8 可以看出,不同来流量下分流比随相对闸门开度变化幅度一致,呈近似成反比关系,当Q为39.70~28.93 L/s 时,分流比变化趋势较大;当Q为25.35 L/s 时,变化趋势最平缓,即在小流量下闸门开度对分流比的影响较小。当来流量一定时,随着闸门开度的增加,主渠过流量增大,侧渠分流量减小,从而使分流比降低,最大降幅为16.78%。

图8 不同来流量下分流比与相对闸门开度关系Fig.8 Relation between diverting ratio and relative gate opening at different inlet flows
4 结论
本研究对梯形渠道分水口在不同来流量和闸门开度下进行了试验研究,分析了主渠道沿程水面线的变化,以及侧渠流量系数与其影响因素之间的关系,得到了以下主要结论:
(1)梯形主渠沿程水深变化规律基本一致,整体变化趋势为先降低后升高再降低。自由出流条件下,当来流量在25.35、28.93、32.38、35.50、39.70 L/s 变化时,闸孔出流和堰流的临界值出现在闸门开度为11、11.6、12、13、14 cm,相对闸门开度e/h变化范围为0.792、0.798、0.808、0.819、0.823,受渠道形状、闸墩形状、流量等因素影响,临界值与理论值存在一定差距,即堰流和闸孔出流的分界并非一个定值。
(2)基于无量纲原理,侧渠流量公式中流量系数m与弗劳德数和相对闸门开度e/h有关。不同来流量下,流量系数m均随弗劳德数和相对闸门开度e/h的增大而减小,但经分析发现相对闸门开度大于弗劳德数对流量系数的影响。因此拟合出流量系数m与闸门开度e、闸前水深h之间的关系式,从而得到侧渠流量,用试验数据进行验证,平均误差为0.75%。
(3)不同来流量下分流比随相对闸门开度的增大而减小,且大流量下分流比变化趋势较大,最大降幅为16.78%。即在小流量下闸门开度对分流比的影响较小。

