基于超宽带技术的无线定位系统设计

陈 雷

(珠海优特电力科技股份有限公司，广东 珠海 519000)

0 引言

随着“智能城市”、“工业4.0”、“中国制造2025”等新兴概念不断涌入人们的视野，基于位置信息的定位服务(LBS, location-based service)也越来越引起人们的重视，定位技术渐渐被广泛的应用于各行各业之中[1-2]。在商业领域，定位技术可以为商家提供更为高效的广告服务，实现商品信息的准确投递；在交通领域，基于定位技术的导航服务，可以提供路线引导、躲避拥堵、路况识别等功能，解决了人们的出行烦恼；在公共安全领域，定位技术提供的位置信息，在面临紧急事故时，为人员的快速搜救创造了条件；在工业领域，定位技术为安全生产管控系统提供人员和设备的位置信息，保障了生产过程中的人员安全和设备安全[2-5]。

近年来，无线通信技术突飞猛进，带动了无线定位技术的发展，快速补充了定位技术领域内的空白，推动了相关技术的普及与应用[2]。借助蓝牙、ZigBee、Wi-Fi、射频识别(RFID, radio frequency identification)以及超宽带(UWB, ultra wide band)等新兴无线通信技术的出现与发展，大大提升了无线定位系统的精度和响应速度，更好地满足了人们对定位服务的需求[6]。其中，UWB定位技术具有抗多径效应、低功耗、低复杂性等优点，被广泛的应用于高精度定位场景中[7-8]。

无线定位系统，基于无线信号的传播特点来解析精确的位置信息，常用的定位手段有：接收信号强度(RSSI, received signal strength indication)、信号传播时间(ToF, time of fligh)、信号到达接收机的时间差(TDoA, time difference of arrival)、信号到达角度(AoA, angle of arrival)等[6,9]。

RSSI定位手段是通过测量信号的接收强度来求解位置信息。常用的方法有两种：

1)指纹定位：将多个信号的接收强度与预存的数据库进行比对，找到最为匹配的数据结果对应的位置信息，即为定位结果[10-11]；

2)基于距离值的定位方法：根据信号传播模型，利用信号强度值计算信号传播的距离，再利用三角定位等算法求解出定位结果[12-13]。

由于信号强度的衰减情况受环境影响剧烈，且对于信号的传播难以精确建模，导致RSSI定位手段的定位精度较低，无法满足工程应用的需要[10-14]。

ToF定位手段是一种基于距离值的定位方法，通过记录信号的发送时刻和接收时刻，计算信号在传播过程中的时间，再利用三角定位等算法求解定位结果[15-16]。常用的测距方法有单边双向测距和双边双向测距[17]。

相比于RSSI定位手段，ToF定位手段对硬件的要求更高(需要精准地标记信号的收发时刻)，能够达到的定位精度也更高[16-21]。随着电子器件和移动终端的快速发展，ToF定位手段已经展现出比RSSI定位手段更广阔的应用场景[21]。

TDoA定位手段通过记录信号到达各个接收机的不同时刻的差值，利用构造双曲线方程的方式求解位置信息[22-23]。使用该手段进行定位的前提是各接收机之间实现时钟同步，时钟同步差异越小，定位精度越高[24-25]。

TDoA定位手段的定位精度与ToF定位手段基本相当，虽然算法较为复杂，但是系统可靠性更强，所以也被广泛地应用于各种无线定位系统中[22-26]。

AoA定位手段通过使用具有方向性的接收天线阵列来感知信号的入射角，再利用三角定位法等算法计算位置坐标[27]。

相比于ToF和TDoA定位手段，AoA定位对于硬件提出了更高的要求，且更易受到环境的影响，制约了该种技术手段的应用[28]。所以，多数场景下，AoA定位作为一种补充定位手段，以提升整个定位系统的定位精度[29]。

然而，无论应用哪种定位手段，都无法完全避免环境对于信号传播的影响，进而影响定位精度；尤其是在复杂环境中，由于多径效应的影响，定位精度损失严重[30]。为了解决多径问题，文献[30-34] 提出了一系列算法及流程，但是在面对真正的工程问题时，这些方法对于定位精度的优化效果有限，无法满足工程应用的要求。

针对这个问题，本文提出了一种基于残留误差的聚类算法，并将之应用于现有的UWB定位系统中。经过工程现场实测数据的检验，该算法能够有效提升定位系统的定位精度，满足工程实际对位置服务精度的要求；同时，使用该算法虽然会占用更多的内存(小于800 MB)、且消耗更多的时间(小于10 ms)，但是不影响工程中的使用。所以，本算法的提出与应用，为无线定位技术的推广提供了重要的技术保障。

在本文以下章节中，章节1介绍了UWB定位系统的典型架构和基本原理；章节2提出了基于残留误差的聚类算法；章节3描述了工程现场测试环境、相关参数，并展示了测试结果；最终，在章节4总结全文。

1 UWB定位系统典型架构和基本原理

典型的UWB定位系统基本架构如图1所示，由定位标签、定位基站、以及定位服务器组成[35]。

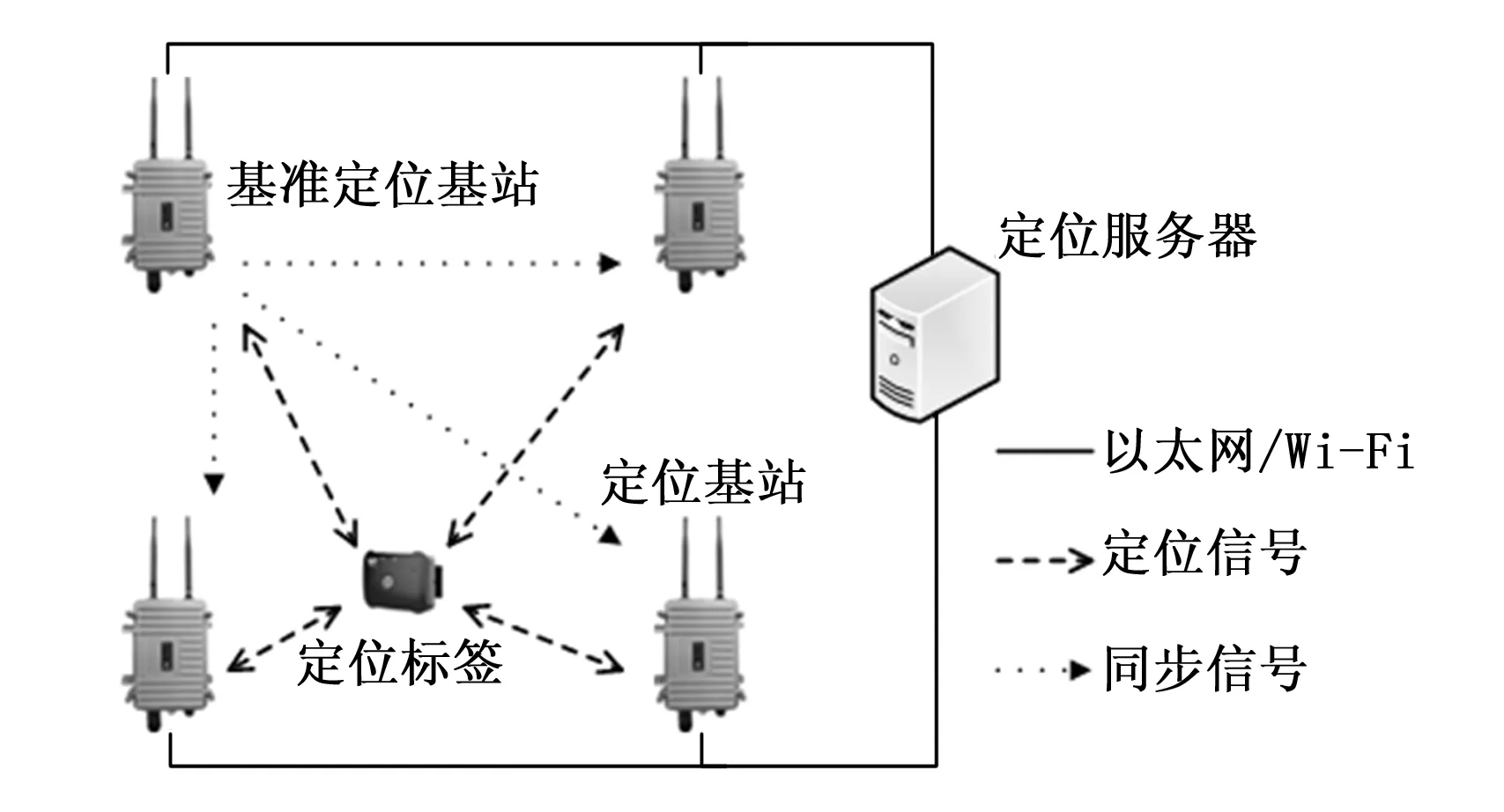
图1 UWB无线定位系统架构

1.1 定位标签

定位标签具有UWB通信模组，可以使用UWB信号与定位基站进行通信，记录通信报文的发送和接收时间，并将定位标签ID与这些时间信息打包放入通信报文中。

1.2 定位基站

定位基站具有UWB通信模组、以太网/Wi-Fi通信模组和数据处理单元。定位基站能够使用UWB信号与定位标签通信，记录报文的收发时间，并将这些时间信息与定位标签在报文中封装的时间信息，通过以太网/Wi-Fi通信模组传输给定位服务器。

此外，在定位基站中选取一个基站作为基准基站，由该基站发出UWB时钟同步信号，其他基站接收UWB时钟同步信号，并将同步信号的收发时间通过以太网/Wi-Fi通信模组传输给定位服务器。

1.3 定位服务器

定位服务器主要有数据处理单元和定位计算单元。数据处理单元提取来自于定位基站的网络报文中的定位信号的收发时间与同步信号的收发时间，并经过计算得到原始定位数据。定位计算单元利用这些定位数据进行算法求解，即可得到定位标签的位置信息。

UWB定位系统的定位过程如图2和图3所示。

图2 UWB定位系统定位过程图

1)基准定位基站周期性发送时钟同步信号给其他定位基站，基准定位基站将同步信号发送时刻(如图3中基准定位基站发送同步信号的时间点为{tS1,0,tS2,0,tS3,0})上送给定位服务器，其他定位基站将同步信号接收时刻(如图3中编号为i的定位基站接收同步信号的时间点为{tS1,i,tS2,i,tS3,i})上送给定位服务器；

2)定位标签与定位基站之间周期性使用定位信号进行通信，定位标签和定位基站都标记定位信号的收发时间，并由定位基站将这些时间信息上送给定位服务器(图3为双边双向测距模式，其中，定位标签和基准定位基站的定位信号对应的时间信息有{t1,t2,0,t3,0,t4,0,t5,t6,0}，定位标签和编号为i的定位基站的定位信号对应的时间信息有{t1,t2,i,t3,i,t4,i,t5,t6,i})；

3)定位服务器内数据处理单元接收到定位信号收发时刻和同步信号收发时刻，利用时钟同步算法[26]，计算得到原始的定位数据(利用图3中的时间信息{tS1,0,tS2,0,tS1,i,tS2,i,t2,0,t2,i}计算得到定位标签与定位基站i的距离减去定位标签与基准基站的距离的差值信息，作为TDoA定位手段下的定位数据；利用图3中的时间信息{t1,t2,i,t3,i,t4,i,t5,t6,i}计算得到定位标签与定位基站i的距离，作为ToF定位手段下的定位数据)，并将定位数据输入给定位计算单元；

图3 同步与定位过程中的时间信息

4)定位服务器内定位计算单元接收到定位数据，利用定位算法计算，即可得到定位标签的坐标结果。

所以，该系统可以同时兼容ToF和TDoA定位手段。对于ToF定位数据，该系统默认使用[36]中的算法；对于TDoA定位数据，该系统默认使用[37]中的算法，也支持其他算法的扩展。

为了提升该定位系统的定位精度，满足复杂工程环境下的定位性能需求，在定位服务器的定位计算单元内部、进行定位计算的原有过程中(如图4中灰色部分)，引入“定位数据的重新组合”与“利用残留误差对定位结果进行聚类”两个算法流程(如图4中白色部分，具体的算法流程在下一个章节进行详述)，其中：

图4 定位计算单元内算法流程示意图(白色部分为新引入算法流程)

1)定位数据的重新组合。引入这个算法流程，一方面可以提升定位数据的利用率，另一方面，还可以将测量精度较高的定位数据形成数据组合，使用这种数据组合计算得到的定位结果，其精度较高，从源头上过滤掉那些受环境影响较大的定位数据。

2)利用残留误差对定位结果进行聚类。引入这个算法流程，降低残留误差较大的计算结果对最终定位结果的影响，并利用聚类算法处理不同组合得到的坐标结果，提升了定位计算的精度。

2 算法及流程设计

在定位区域内，部署了N个定位基站(N>4)，每个定位基站的坐标为(Xi,Yi,Zi)，基站编号i=1～N。每个定位基站都对应一个定位数据，记为li：当使用ToF定位手段时，定位数据li为定位标签与基站i之间的距离；当使用TDoA定位手段时，定位数据li为定位标签到基站i的距离减去定位标签到基准基站的距离的差值，基准基站的坐标为(X0,Y0,Z0)。

在三维空间内，需要不少于4个基站就能完成定位计算。为了最大化的利用这N个定位数据，如图5所示，将这些定位数据进行组合，分别使用4～N个定位数据进行定位计算，则一共有M组定位数据的组合，M的值为：

图5 定位结果解算流程图

(1)

设第m组数据组合的表达式为：

(2)

其中:m=1～M,利用该数据组合l(m)，根据[36-37]中的算法，可以计算得到坐标结果为P(m)=(x(m),y(m),z(m))，进而反推出对应于数据组合的估算数据：

(3)

(4)

(5)

其中:i=1～n。

(6)

当残留误差ε(m)大于门限ξ1时，认为该坐标结果P(m)=(x(m),y(m),z(m))无效，丢弃该结果；否则，认为该结果有效，进入聚类计算。门限ξ1的取值与定位精度有关：当定位精度越高时，ξ1的取值越小；默认值为0.5米。

从有效的坐标结果中，利用K-Means聚类法[38-39]，随机选取K个解初始质心，记为：

(7)

式中,下标 “(1)” 表示第一次聚类迭代。

遍历所有有效坐标结果，分别计算每个坐标结果P(m)=(x(m),y(m),z(m))与这K个质心的欧式距离：

(8)

(9)

(10)

其中:α为权重参数，取值范围为0≤α≤1。在使用时，α的取值与定位精度有关：当定位精度越高时，α的取值越大；默认值为0.5。

(11)

式中,下标 “(2)” 表示第二次聚类迭代。

计算所有质心在更新前后的距离的差值的和，记为δ(2)：

(12)

δ(2)>ξ2且γ<ξ3

(13)

其中:ξ2为质心距离差值门限，γ为迭代次数，ξ3为迭代次数上限。系统要求达到的定位精度越高，ξ2的取值越小，ξ3的取值越大。此外，设计这两个门限值时，也要考虑系统内的内存资源和定位响应时间，ξ2的取值越小，ξ3的取值越大时，计算所占用的内存资源越大，耗时越久。

(14)

3 实验结果与分析

为了验证本文提出的算法流程对原有定位系统定位性能的优化效果，在浙江省某变电站内部署了35个定位基站，覆盖了约60米×70米大小的室外区域。如图6所示，区域内存在两座大型变压器(主变1和主变2)、一座主控楼(在主控楼内不做定位要求)以及一些龙门架、电抗器、机器人坞等建筑，图中“×”标识的位置部署了定位基站。

在定位场地内，分别进行静态测试和动态测试：静态测试是指在场地内选择若干位置点(如图6中的“⊙”所标识的6个静态测试点位)，测绘位置点坐标；然后将定位标签依次放置于这些位置上保持不动，分别测试5～10分钟，观察定位坐标与测绘坐标的偏差，并计算定位坐标与测绘坐标的欧式距离dj作为定位系统的偏差值 (j表示第j次定位，偏差值dj如图7静态测试所示：定位坐标Pj到测绘坐标p1的距离，即为dj)。

图6 变电站室外定位区域及基站部署图

图7 定位偏差示意图

动态测试是指在场地内选择固定的运动路线(如图6中箭头“→”标识的路径为动态测试路径)，测绘出路线的坐标；再令人员佩戴定位标签沿着路线运动，观察定位结果与测绘路线的偏差，并计算定位结果到路线的垂线距离dj作为定位结果的偏差值 (j表示第j次定位，偏差值dj如图7动态测试所示：测绘行进路线的起点坐标p2和终点坐标p3，计算定位坐标Pj到线段的垂线距离，即为dj)。

使用统计量σ95表征定位精度，其含义是指95%的定位结果的偏差值都小于或者等于σ95。即，如果使用{dj}表征定位结果偏差值dj的集合 (j表示第j次定位)，则σ95是大于或者等于{dj}中95%的元素值的最小值，可以表示为：

σ95=argmin{d≥{dj}中95%的元素值}

(15)

可以看出σ95值越大，则表示定位结果距离测绘值越远，即定位精度越低。

测试过程中的参数如表1中给出。在测试过程中，为了便于说明描述，将图4中灰色部分的原有算法流程记为“原算法”，图4中引入的白色部分后的算法流程记为“新算法”。

表1 定位测试参数表格

点位1的静态测试结果如图8所示，图中横轴为X坐标，纵轴为Y坐标，单位为米，格子粒度为0.1米；图中“◇”表示测绘点坐标，“×”表示“原算法”定位结果，“·”表示“新算法”定位结果；虚线表示使用“原算法”得到的σ的值覆盖的范围，实线表示使用“新算法”得到的σ95的值覆盖的范围。

图8 点位1定位结果分布图

通过对比可以发现，使用“新算法”得到的坐标点分布的聚合性更强，且更贴近于该点的测绘值。通过统计，得到“原算法”与“新算法”的σ95值分别为0.39米和0.21米。所以，可以得出结论：使用“新算法”可以有效提高无线定位系统的定位精度。

使用相同的统计手段，处理其他定位点的测试结果，得到定位精度的统计结果如表2所示。可以看出，使用“新算法”进行定位计算得到的数值更小，意味着该算法的结果的定位精度更高，尤其是在遮挡较为严重的区域(如点位2)，该算法的优势更为明显。

表2 静态测试各点的统计结果 m

动态测试的定位轨迹以及实际路线如图9所示，统计结果如表3所示。在图9中，实线表示测绘的运动路径，“×”表示“原算法”结果，“·”表示“新算法”结果。

表3 动态测试各点的统计结果 m

图9 动态测试定位轨迹图

从图9中可以看出，使用“新算法”的定位结果在进行动态测试时，定位轨迹更为平滑，且与实际运动路径最为接近；尤其是在主变附近、主控楼附近这种存在明显遮挡的区域，使用“新算法”对无线定位系统的定位轨迹提升效果更为明显。此外，从表3的数据统计值也可以看出，在运动过程中，使用“新算法”的定位结果精度更高。

综合考虑图8和图9以及表2和和表3的结果，可以发现：无论是静态测试还是动态测试，“新算法”的定位精度都能保持在0.5 m以内，在一些较为空旷的区域，定位精度甚至可达10 cm。而且，相比于“原算法”，“新算法”在定位精度方面有了进一步的提升，尤其是在遮挡较为严重的区域，定位精度的提升更为明显。

此外，为了验证该无线定位系统的工程实施可行性，在定位测试过程中，记录了定位过程中的平均内存开销，并统计每次定位解算的运算耗时(定位服务器基于WIN7系统、I5处理器、8 G内存)，统计结果如表4所示。

表4 定位过程中的资源占用统计

通过对比可以发现，引入“定位数据的重新组合”与“利用残留误差对定位结果进行聚类”两个算法流程的“新算法”，其计算过程会占用更多的内存、且消耗更多的时间，但是其性能依然满足工程应用的需求。

4 结束语

当前基于超宽带技术的无线定位系统，很容易受到定位场地中的环境干扰，在定位数据源头上引入了较大的误差，导致定位精度的降低，限制了无线定位系统在工程应用中的推广。本文针对这种存在于基于超宽带技术的无线定位系统的问题，提出了一种基于残留误差的聚类算法，在提高了原始数据利用率的同时，降低了计算结果中残留误差的影响，进而实现了定位精度的提升。本文还提供了使用该算法的无线定位系统进行工程实测的数据结果，证明了该算法对于无线定位系统性能提升有较好的效果。