抽象函数巧思维 求解规律妙归纳

安徽省淮北市第七中学 (235099) 王 凯

1.真题呈现

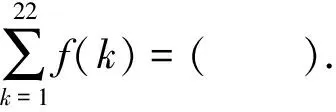
A.-21 B.-22 C.-23 D.-24

这里2022年高考数学全国乙卷理科第12题，此题以两个抽象函数之间的关系式以及其中一个抽象函数图象的对称性来创设情境，求解另一个抽象函数中连续正整数所对应的自变量所对应的函数值之和.对于此类抽象函数问题，可以利用函数的基本性质(包括奇偶性、单调性、对称性与周期性等)来分析与转化，构建关系，寻找规律，借助函数值的分析与求解来处理，对数学抽象、直观想象、逻辑推理等核心素养都有较高的要求.

2.真题破解

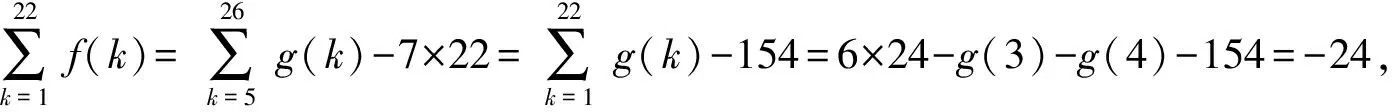
评析：以上解法主要是根据抽象函数图象的对称性，以及给定的关系式，通过代换处理与赋值处理，结合函数的奇偶性与周期性的定义来判断抽象函数的基本性质，并结合递推关系式确定一个周期内的对应函数值，进而综合函数的基本性质来分析与求解.实际上，定义法是解决抽象函数问题中最常用的技巧方法，求解关键在于应抓住函数的基本性质(奇偶性、周期性等)加以逻辑推理，结合相关定义加以分析与判断性质类型，这为进一步的求值与应用提供条件.

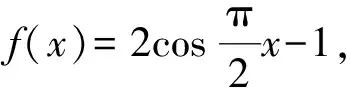
评析：以上解法主要是根据抽象函数图象的对称性，以及给定的关系式，确定函数的奇偶性，并在此基础上合理构建特殊的满足条件的三角函数，借助特殊函数求值来分析与解决.实际上，抽象函数的难点就在于“抽象”二字，如果能化抽象为具体，那么问题就能迎刃而解.而在基本初等函数中，相应图象既有对称轴，又有对称中心的是三角函数.巧妙合理构造出满足条件的特殊函数是角法中的关键.

3.链接高考

近年高考试卷中都有此类抽象函数的基本性质的综合应用问题，形式各样，变化多端.但是都能找到抽象函数的“影子”.

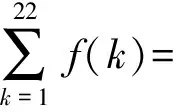
A.-3 B.-2 C.0 D.1

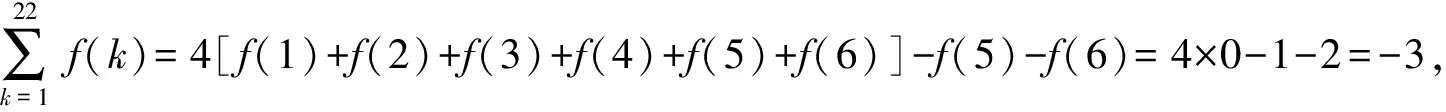
例2 已知函数f(x)，g(x)的定义域均为R，且f(x)+g(2-x)=5，g(x)-f(x-4)=7.若y=g(x)的图象关于直线x=2对称，g(2)=4，则f(2023)=( ).

A.-1 B.-2 C.-3 D.1

解析：易得函数f(x)的周期为4，所以f(2023)=f(505×3+3)=f(3)=-1，故选A.

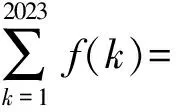
A.-2022 B.-2023 C.-2024 D.-2025

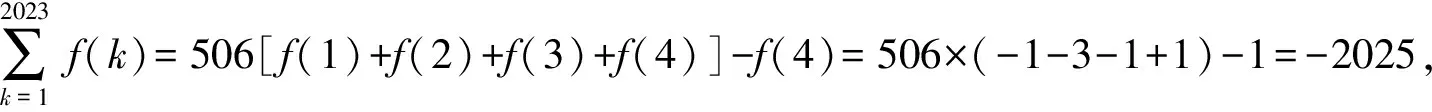
4.教学启示

(1)重视函数的图象

函数的图象能更好的理解函数的变化，函数的对称性最突出的作用是“知一半而得全部”，即一旦函数具备对称性，则只需要分析一侧的性质，便可得到整个函数的性质，这些性质主要体现在以下方面：可利用对称性求得某些点的函数值；在作图时可作出函数的一侧图象，再利用对称性得到另一侧的图象；极值点关于对称轴(或对称中心)对称；在轴对称函数中，关于对称轴对称的两个单调区间单调性相反；在中心对称函数中，关于对称中心对称的两个单调区间单调性相同；等等.

(2)用好函数的对称性

一般地，涉及函数图象的对称性问题都与以下两种等价性质相关：

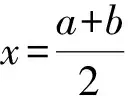
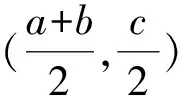
(3)巧用函数的周期性