一道省模考题引发的逻辑问题

广东省南雄市第一中学 (512400) 黄学波

一、问题缘起

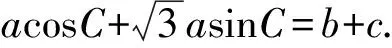
化简上述三个论断，求出角的值或角的关系，并以其中两个论断作为条件，余下的一个论断作为结论，写出所有可能的真命题.(不必证明)

其参考答案如下:

论断②，∵c=2bcosB，由正弦定理得sinC=2sinBcosB=sin2B，∵C∈(0,π)，2B∈(0,2π)，∴C=2B或C+2B=π.

以其中两个论断作为条件，余下的一个论断作为结论，所有可能的真命题有：

①③⟹②和①②⟹③.

在一次教研活动中，有老师对参考答案提出了质疑：对答案中的①③⟹②没有异议，但对①②⟹③，有人认为真命题，也有人认为是假命题，还有人认为②③⟹②与①③⟹②形式上一样，也应该是真命题.

究竟参考答案有没有问题呢？为了弄清楚这个问题，我们必须用逻辑代数或数理逻辑知识进行分析，才能得出让人信服的结论.

二、逻辑知识

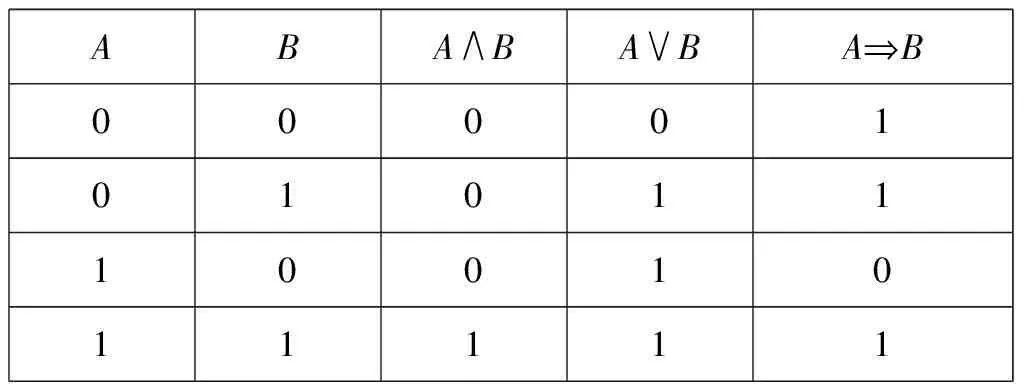
由逻辑代数或数理逻辑知识，我们知道，对于A∧B、A∨B及A⟹B有如下逻辑真值表(1表示“真”，0表示“假”)：

ABA∧BA∨BA⇒B00001010111001011111

从真值表可知，当且仅当A真、B假时，A⟹B为假.用真值表或由定义(符号“=df”表示定义的意思，“=”表示左右两边的逻辑式真价相等，即常说的“等价”)：A⟹B=df(A∧B)=A∨B，结合逻辑运算，我们可以证明：A∨B⟹C=(A⟹C)∧(B⟹C).下面用定义和逻辑运算给出证明.

∵A∨B⟹C=(A∨B)∨C=(A∧B)∨C

一般地，有A1∨A2∨…∨An⟹C=(A1⟹C)∧(A2⟹C)∧…∧(An⟹C).

这个结论解释了一个全称命题A1∨A2∨…∨An⟹C为真，为什么必须Ai⟹C(i=1,2,…,n)均为真的理由.

同时易知，A∨B⟹C≠(A⟹C)∨(B⟹C).

同理，可证：A⟹B∨C=(A⟹B)∨(A⟹C)，一般地有A⟹C1∨C2∨…∨Cn=(A⟹C1)∨(A⟹C2)∨…∨(A⟹Cn).

三、问题分析

有了前面的有关命题的理论知识后，我们从逻辑的视角对前面的问题加以分析.

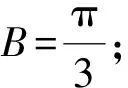
那么①②⟹③等价于R∧M∧(S∨P)⟹N=(R∧M∧S)∨(R∧M∧P)⟹N=((R∧M∧S)⟹N)∧((R∧M∧P)⟹N).

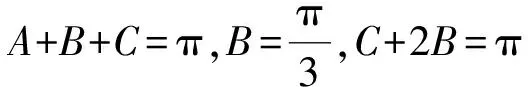
综上可知，①②⟹③为真.

而②③⟹①等价于R∧(S∨P)∧N⟹M=(R∧S∧N)∨(R∧P∧N)⟹M=(R∧S∧N⟹M)∧(R∧P∧N⟹M).

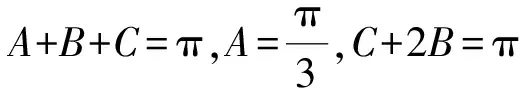
综上可知，②③⟹①为假.

而①③⟹②等价于R∧M∧N⟹S∨P=(R∧M∧N⟹S)∨(R∧M∧N⟹P).

综合以上分析，可知参考答案正确.

四、变式应用

在本次教研活动中，还有老师提出下面的问题，认为不好判断它们的真假：

问题：判定下列三个命题的真假：

(A)若x=1,3x+y=5或x=y,则y=1；

(B)若x=1,y=1,则3x+y=5或x=y；

(C)若y=1,3x+y=5或x=y,则x=1.

现在我们用上述逻辑知识给予分析判断.

解：为了了解各命题的逻辑结构及其相互关系，和前面一样，我们用M表示“x=1”，用N表示“y=1”，用S表示“3x+y=5”，用P表示“x=y”.

对于(A)，由于M∧(S∨P)⟹N=(M∧S)∨(M∧P)⟹N=(M∧S⟹N)∧(M∧P⟹N),即命题“若x=1,3x+y=5或x=y,则y=1”为真，等价于命题“若x=1,3x+y=5，则y=1”与命题“若x=1,x=y,则y=1”同时为真.而命题“若x=1,3x+y=5，则y=1”为假，命题“若x=1,x=y,则y=1”为真，于是(A)为假.

对于(B),由于M∧N⟹S∨P=(M∧N⟹S)∨(M∧N⟹P),即命题“若x=1,y=1,则3x+y=5或x=y”为真，等价于命题“若x=1,y=1,则3x+y=5”为真或命题“若x=1,y=1,则x=y”为真.虽然“若x=1,y=1,则3x+y=5”为假，但命题“若x=1,y=1,则x=y”为真，所以(B)仍为真.

对于(C)，类似的可判断其为假.

小结：对于结构较复杂的命题，判断其真假必须利用逻辑真值表并结合逻辑运算才能厘清命题的逻辑结构，从而正确地判断其真假.