基于累积前景理论的应急物资路径选择研究

宋少忠，杜 影*，尚雨晴，辛 钢

(1. 吉林工程技术师范学院，吉林 长春 130052;2. 吉林工商学院，吉林 长春 130500)

0 引言

新冠疫情防控期间，在城乡居民静态封闭式居家隔离情况下，为有效应对生活物资出现暂时性短缺等问题，合理选择城乡各区域应急物资供应点，实施配套的精准保供调度至关重要。

目前，有很多研究人员在不同的背景下针对应急物资的配送优化问题进行建模，薛啟瑞等人[1]考虑货物紧缺程度情况下，提出近似算法GA*，对近似算法的计算复杂度进行了研究,以中国云南省某地区地震灾区的交通运输路网为例,证明了模型和方法的合理性。董雅文等人[2]基于应急物资供给点的库存进行分类构建多目标优化模型，通过非支配排序遗传算法(NSGA-Ⅱ)，获得模型的最优解集，进而提供大量分配方案供决策者依据实际需要选择。王小纯等人[3]在不确定环境下震后的情况对应急物资配送模型研究，采用三角模糊数来描述震后道路容量，进而建立了基于可信性测度的模糊机会约束规划模型，但这种模糊的刻画具有一定的主观性。张笑晨等人[4]从路径交通情况考虑，针对获取到的路径识别，提出一种基于物联网定位技术的应急物资运送路径选择模型，选择合适的运送路径，能够有效规避拥挤路段，具有一定的实用性。以上的研究人员从不同的角度来研究应急物资路径选择，都是在假设决策者完全理性的条件下，并没有考虑到决策者并非完全理性的抉择。而累积前景理论[5]不用按照这样的决策者完全理性的假设去解决不确定性条件下的决策问题。

前景理论是心理学及行为科学的研究成果。在决策过程中每个决策者都不是绝对理性，而是属于有限理性的，他们对信息接收的情况是有限的，因此判断信息也是不完全确定。决策者在决策过程中容易接受相对于心理期望值参照点较为满意的结果。Fang等人[6]将累积前景理论应用于犹豫模糊TOPSIS多属性决策方法，验证了该方法在决策过程中的可行性。王涛等人[7]利用奖惩罚劣算子和灰关联决策系数将累积前景理论的价值函数进行改进，其中的相关系数对多个零售商的评价指标进行处理，计算实例的结果表明，综合前景价值能更好地反映用户的真实评价。华成旭等人[8]将累积前景理论应用于大学生出行模式选择的预测，得出累积前景理论更适合于大学生出行模式的预测。相关研究表明，累积前景理论在各个领域的应用中具有一定的适应性。应急物资路径的选择是一个典型的不确定性和多属性决策问题，因此可将其推广到应急物资路径选择研究中。

1 数学模型的建立

1.1 问题描述

1.2 路径的运输时间

由于疫情发生的严重程度各不相同，进而每个路段的灾害强度有轻有重；在限制运输速度和运输时间情况下，该路段最大运行速度Vmax(本文中各个路径的最大运行速度取60km/h)与实际行驶速度V不符，所以实际行驶速度计算公式如下[9]：

(1)

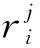
(2)

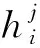
综上所述，应急物流从提供点到接受点的第Ci条路径所需的时间Ti的公式为：

(3)

1.3 最优路径的评价

1.3.1 价值函数的确定

价值函数是反映集合中元素间序关系的函数，也可以用来衡量各个路径实际效用参考点的偏离，其表达式如下[10]:

(4)

式中，Δx为决策方案相对于参考值的差值，Δx大于零表示收益，Δx小于零表示损失。由运输时间可建立一个时间参考点，小于这个时间参考点代表收益，而大于则代表损失。参数α为收益敏感系数，β为损失敏感系数，λ为损失规避系数，通常α=β=0.88,λ=2.25。

1.3.2 权重函数的确定

权重是指整体评价中相对重要程度，而在积累前景理论中则用权重函数来衡量人的心理作用。决策者普遍拥有两种态度，偏向于高估低概率事件和低估高概率事件，在面对一些结果的时候，决策者在面临获利的时候是风险规避的，在面临损失的时候是风险喜好的，其表达式如下：

(5)

其中p为一件事发生的实际概率；w(p)为主观权重概率;λ为收益感知概率系数；δ为损失感知概率系数，λ=0.61,δ=0.69。

1.4 时间参考点的设置

本文优先以时间为参考点，它取值的大小直接影响到决策的有效性。通过美国联邦公路局的路阻函数[12]进行计算，可以求出应急物流运输过程中的时间参考点tc(min)，其公式为：

(6)

其中，timin为从物资提供点i到物资接受点的所有路径中时间最小值；由美国联邦公路局路阻函数模型中公式(6)的参数为：

1.5 最优路径的选择

本文在应用累积前景理论的路径选择过程中，应急物资所选的最优路径应为前景值最大对应的路径EXmax，即：

EXj=vj(Δxj)wj(pj),j=1,2,……,a0

(7)

EXmax=max{EXJ},j=1,2,……,a0

(8)

其中vj(Δxj)与wj(pj)分别为利用公式(4)和公式(5)计算的第j个路线的价值函数值与权重函数值。

2 实例分析

以在模拟某个地区道路交通网络[13]为例，该地区现在急需a,b,c三种疫情物资，现在共有十二个物资供应地区C1,C2,C3,C4,C5,C6,C8,C9,C10,C11,C12，C13可以提供此三种物资且C7,C14分别为中转点和终点，道路交通图如图1。C14所需的a，b，c的数量分别为100t，30t，75t。各路段的距离，路径通过风险值和安全通过的概率见表1。十二个物资供应地区可以提供的物资数量见表7。要求应急物流送达的时间不超过三小时。需要选取最少的物资供应地区和最合适的行驶路线。

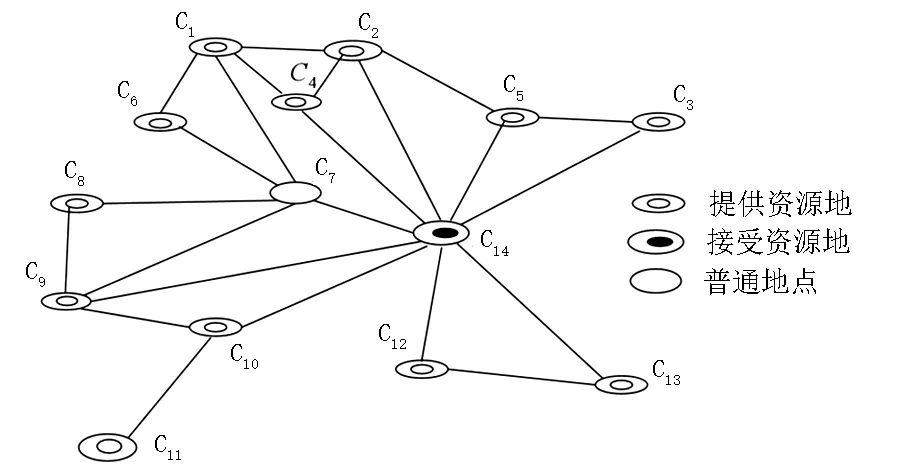
图1 道路交通网络示意图

表1 图1中节点间数据

接下来以C1作为物资供应地区为例，系统的分析由C1出发到达终点C14的最佳行驶路线。先将图1中由C1到C14的所有路线提取出来分析，如图2。由表1中数据经过文中公式(1)(2)计算可得每段路程的速度与时间如表2，由图2可知C1到C14的所有可行线路见表3。

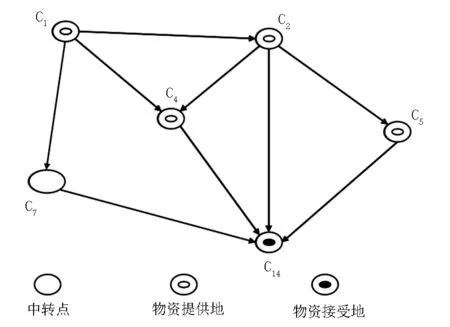
图2 以为物资供应点到达物资需求点的道路交通网络示意图

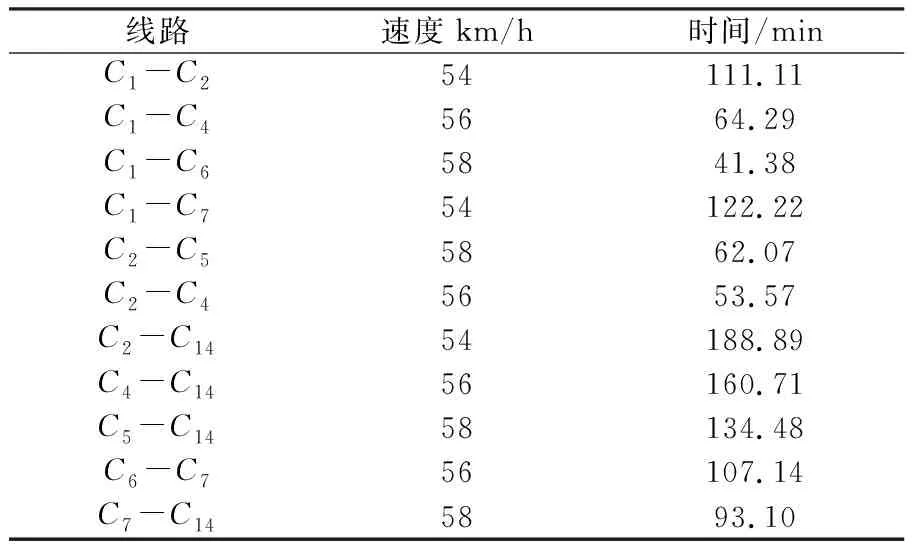
表2 图2中每段路程的速度与时间

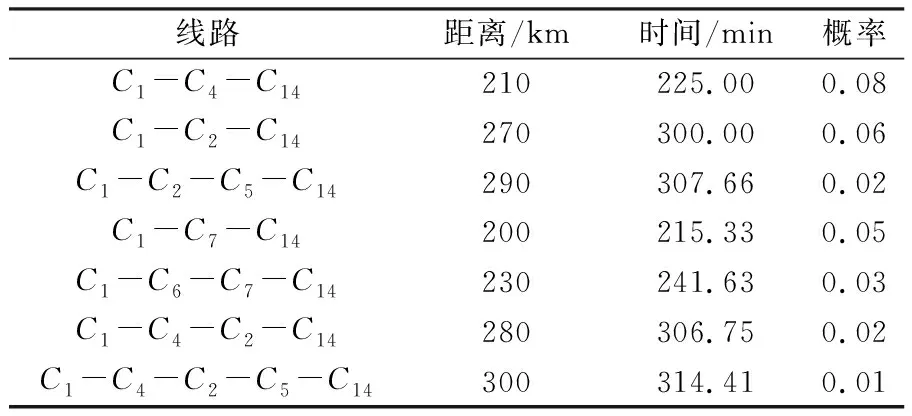
表3 到的所有可行线路

由表3数据可知，t0min=215.33min,根据公式(6)可计算出时间参考点tc=228.56min。根据文中公式(4)(5)(7)计算得到各线路的价值函数值，权重函数值以及前景值，见表4。

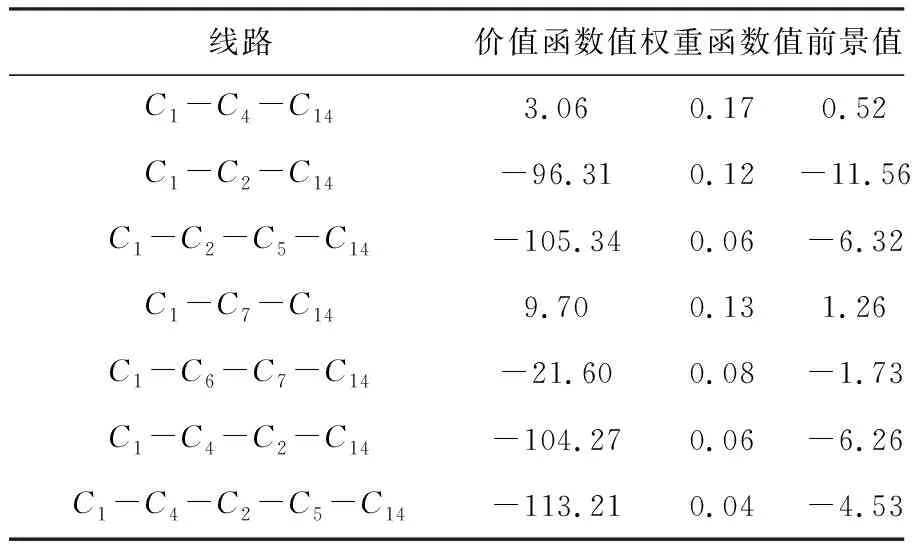
表4 到的所有可行线路的前景值

根据表4中前景值的大小分析可知为最佳的行驶线路，同理，图1中各物资供应地区到物资接受地C14的最优行驶路线见下表5。

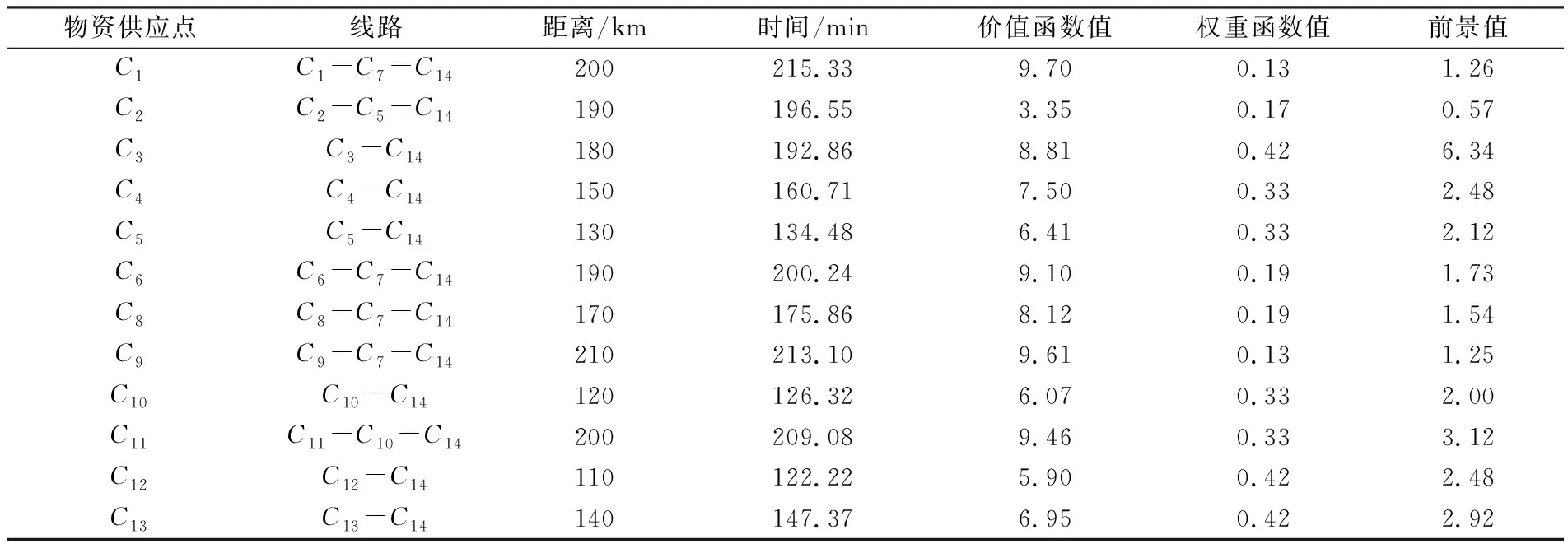
表5 图1所有出发点所选取的最优线路

由于要求运输应急物资时间在三小时之内，所以表5中根据时间长短进行筛选可得表6。各地区可提供a,b,c三种物资数量如表7。

表6 筛选后的物资的供应地区

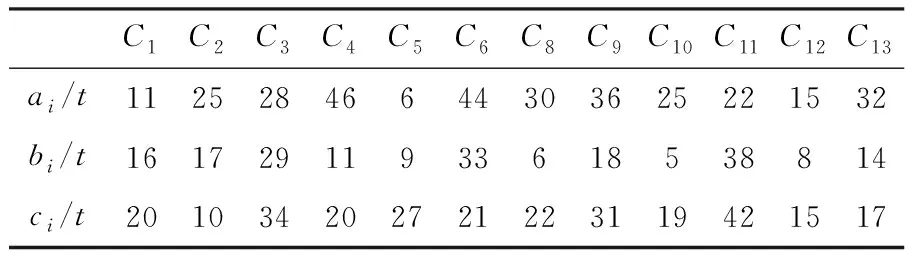
表7 各地区可以提供的物资数量

在考虑时间指标的同时还应考虑各地区可以提供的物资数量，根据表6中剩余的物资供应地区对表7进行筛选，并且由于C14所需物资a=100t为三种物资需求的数量最多，所以直接根据物资a的数量进行由大到小排序，结果见表8。

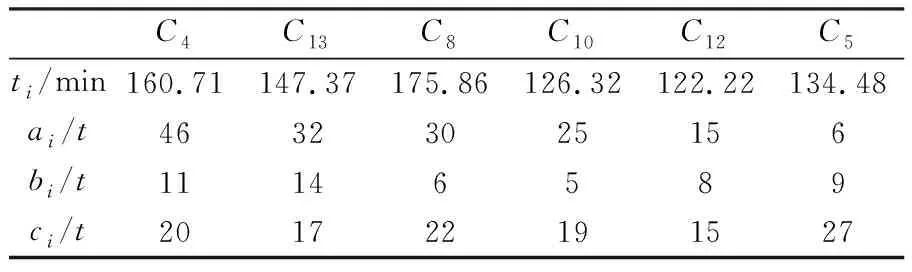
表8 筛选后的可以提供物资的地区并对物资a进行递减排序

由于前三列中a的和大于100t，b的和大于30t，而前三列中c的和小于75t，即从三个地提供物资a、b满足所需的数量，物资c不满足所需的数量，因此最少物资供应地区数量为4个，并对表8中后三列按照c的由大到小重新排序，见表9。

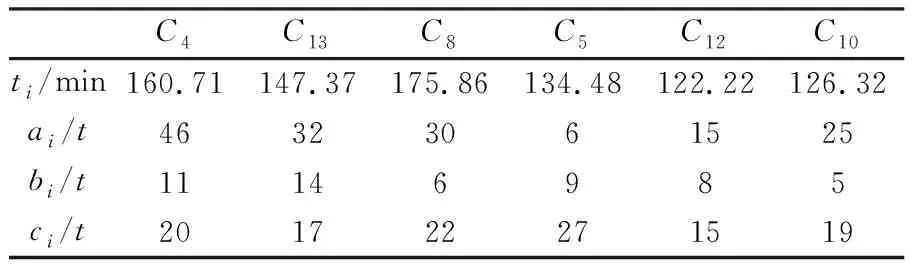
表9 物资c进行递减排序

表9前四列的c的和大于75，所以应选择的物资供应地区为(C4C5C8C13)，通过不同的排列组合，符合物资接受地C14所需物资数量的还有3种供应点组合(C4C5C10C13)，(C4C8C10C13)，(C4C8C10C12)。由表5可知它们的前景值，将前景值加和可得表10。

表10 物资供应点选择方案及前景值之和

基于累积前景理论得到四种物资供应地区组合的前景值之和，前景值之和越大表示所选方案最优，显然(C4C5C8C13)为图1道路交通网络中最优应急物资路径及物资供应点。

3 结论

考虑应急物资运输路径选择过程中的不确定性环境和决策者的有限理性，本文提出一种基于累积前景理论的应急物资路径选择方法。首先，选取运输时间、路段风险度以及物资各供应数为多参考点，然后构建基于多参考点应急物流模型，主要通过构建应急物资路径选择综合累积前景值函数筛选出运输最优路径与物资供应点。最后以多品种、多供应点的应急物流运输网络为例，通过多参考点下的累积前景理论挑选出运输路径及合适的供应点组合。相比只考虑路线的距离，本文方法具有一定的时效性、经济性与安全性，从而为疫情期间物资运输提供一种理论指导。