薄壁齿轮箱结构声强可视化及减振方法研究

刘 岚，亢 琨，席英杰，龚境一，刘 更

(西北工业大学 陕西省机电传动与控制工程实验室， 西安 710072)

0 引言

船用齿轮传动系统中齿轮副的动态啮合激励会通过轴承座传递至齿轮箱体，不仅会使齿轮箱振动，产生辐射噪声，影响船舱的舒适性，还会通过箱体机脚处的螺栓将振动进一步传递到船体，影响船体的安全性。因此，有效控制船舶齿轮箱的振动噪声有着重要意义。目前国内外针对船舶齿轮箱采用的减振降噪措施主要包括[1]：结构改进设计、阻尼材料粘贴、基座导纳匹配和安装形式优化、主动控制等。其中阻尼材料因其高耗能特性可有效实现齿轮箱的减振降噪设计[2-5]，在工程中获得了广泛应用。

目前确定阻尼材料的粘贴区域主要有4种方法：① 声学贡献量分析方法，该方法早期用于车内声场的辐射噪声控制[6-7]，后来逐渐应用到齿轮箱的辐射噪声控制中[8]，但只能用于辐射噪声的控制，与结构的振动控制无直接关联；② 模态应变能分析方法，侯守武[9]通过在齿轮箱模态应变能较大的区域上进行约束阻尼处理，结果表明粘贴约束阻尼后，减速器箱体的振动减小到原始箱体的30%～50%，但该方法只能针对某一阶模态应变能分布进行阻尼材料粘贴；③ 结构优化设计方法，主要将场点上的声压级最小[10]、模态损耗因子最大[11]等作为优化目标，但其计算规模的限制,目前只能应用于简单结构。④ 结构振动声强法，是20世纪70年代由Noiseux[12]将空气声学中的声强理论移植到连续介质领域，结合功率流分析提出的一种新的功率流分析方法。结构声强可以被认为是弹性介质结构中单位截面积上通过的功率流大小，也即振动功率流密度。它不仅可以表示能量大小和方向，同时对该截面进行数值积分即可得到总的振动功率流数值[13]。不过该方法目前仅用于简单平板、壳体、L型板等简单结构，并未应用于齿轮箱等复杂结构上。

本文主要研究如何降低齿轮箱的机脚测点的振动，为了避免前3种方法的劣势，本文从齿轮箱振动能量的角度考虑，通过结构声强可视化方法直观地得到齿轮箱振动能量的分布，更加高效地指导阻尼材料的粘贴，在工程应用中具有一定应用价值。

本文以某船用人字齿行星齿轮箱体为研究对象，提出了基于结构声强可视化的船舶齿轮箱局部附加阻尼减振方法。首先建立箱体的有限元模型，在受某一工况激励的情况下对其振动响应进行分析；其次，通过结构声强可视化技术实现齿轮箱薄壁结构的结构声强幅值云图显示，由此确定出结构振动能量最大的区域；然后对该区域附加阻尼材料降低齿轮箱机脚测点的振动；最后还将局部附加阻尼布局方案与全局附加阻尼布局方案进行对比，证明了本文提出的方法具有更高的材料利用率。

1 结构声强可视化与阻尼减振方法

1.1 结构声强理论

Gavric等[14]和Hambric[15]用有限元方法计算了考虑边界条件下的结构声强，给出了时域内瞬态结构声强的表达式：

Ii(t)=-σij(t)vj(t)i,j=1,2,3

(1)

式中：i，j代表三维空间内的3个方向；σij(t)和vj(t)分别为t时刻j方向上的应力和速度分量。

当结构所受的载荷为正弦激励时，由于速度、应力等参数都是时变常量，假设二者间变化的相位角是φ，从积分的角度对上述公式进行推导，在某一时段内的结构声强值可以通过一个平均量来进行表达，即：

(2)

考虑到相位关系，所以频域内的结构声强可用下式表达：

(3)

根据式(3)可知x、y、z方向上三维实体单元的结构声强可以写为：

(4)

由式(4)可以求得各单元的x、y、z方向的结构声强数值，然后继续求解各单元的结构声强幅值，通过可视化技术得到结构声强幅值云图，将其应用到振动分析领域，可一定程度上描述结构的振动能量分布及传递路径。

1.2 齿轮箱局部附加阻尼减振方法

通常对齿轮箱进行振动响应分析时，通过分析振动响应的频谱图可知，一定存在某个频率处的振动响应最大。如果可以降低该峰值频率下的振动能量，那么就可以实现降低结构振动响应的目标。

因此可以在齿轮箱振动响应分析后，使用ANSYS参数化设计语言(ansys parameter design language，APDL)进行峰值频率处结构声强的计算及可视化显示，根据结构声强幅值云图分析其在受迫振动时的振动能量分布。通过在振动能量大的区域粘贴阻尼材料增加结构耗能，从源头上降低振动能量，从而减少振动能量向齿轮箱机脚螺栓的传递，达到降低机脚测点的振动。

基于上述思想，建立基于结构声强可视化的齿轮箱局部附加阻尼的减振方法，具体流程如图1所示。

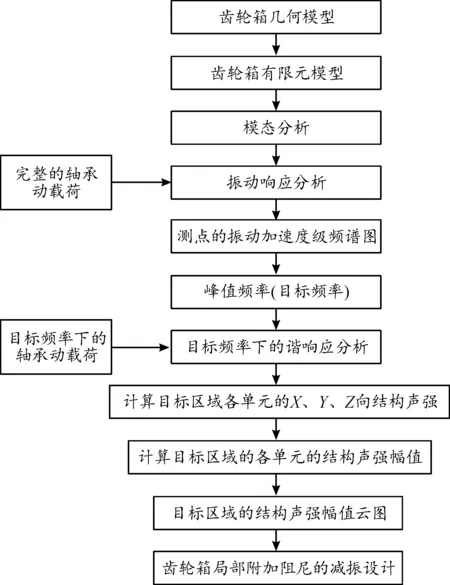
图1 基于结构声强可视化的齿轮箱局部附加阻尼的减振方法流程框图

1) 模态分析

根据齿轮箱的特征，对目标区域划分的六面体网格，其余区域划分四面体网格，建立考虑约束条件的有限元模型。进行模态求解，作为后续振动响应分析和单频激励谐响应分析的基础。

基于模态分析结果使用模态叠加法进行振动响应分析，求解箱体机脚响应测点各个激励频率处的响应，得到各个响应测点的振动加速度级频谱图，由此确定后续谐响应分析和结构声强计算的目标频率。

3) 谐响应分析

在模态分析的基础上，使用模态叠加法进行目标频率下的单频激励谐响应分析，得到节点位移，并在目标频率进行扩展，求解单元应力。

4) 结构声强计算及可视化

使用APDL提取目标区域的各单元的节点位移、单元应力，并在ANSYS内部进行X、Y、Z方向结构声强的计算，计算结构声强幅值。通过DESOL命令将目标区域的单元应力值替换为单元结构声强幅值，查看目标区域的单元应力单元解云图，即可得到目标区域的结构声强幅值云图。

5) 齿轮箱局部附加阻尼的减振设计

根据目标区域的结构声强幅值云图，对齿轮箱振动能量大的区域附加阻尼材料来降低齿轮箱的振动能量，从而降低机脚测点的振动加速度级。

2 齿轮箱模态分析

2.1 分析模型

某大型船用人字齿薄壁行星齿轮箱几何模型如图2所示。其尺寸为长×宽×高=1 200 mm×1 200 mm×1 100 mm，坐标系定义如图2左下角所示。

目前规划的怒江大峡谷国家公园位置都在一定的海拔之上，避开了河谷地带和大多数村社的生产生活区，加之天然林保护工程以及异地扶贫搬迁政策，许多村社也从高海拔山区搬迁到河谷地带。因此，国家公园范围内所涉及的村寨不多。怒江是一个典型的生物多样性和文化多样性丰富，同时又是经济发展较为落后的地区。因此，怒江大峡谷国家公园的建立，除了肩负保护生态的任务之外，还被寄予期望带动怒江州旅游业发展，帮助社区产业转型。本项目选取怒江匹河乡老姆登村进行调研，目的是发现怒江世居民族参与国家公园的机遇与挑战。

图2 齿轮箱几何模型示意图

本文的人字齿行星传动系统主要由差动级轮系(太阳轮，3个行星轮，内齿圈，行星架等)和封闭级轮系(太阳轮，5个行星轮，内齿圈，行星架等)两级传动联结组成，其中封闭级行星架固定。系统功率由输入轴带动差动级太阳轮输入，一部分经差动级行星架输出，另一部分经差动级轮盘传入封闭级太阳轮，差动级行星架输出的差动级功率与封闭级轮盘输出的封闭级功率通过输出轴汇流输出。

因为封闭级行星架固定且与箱体固连，齿轮系统的动态啮合激励通过轴传递至封闭级行星轮的轴承座传递至箱体。因此将封闭级行星轮所在的轴承孔各自耦合到其轴向中心位置形成5个激励加载点，具体加载点的位置如图3所示。由于齿轮箱额定工况为输入功率为200 kW，输入转速4 000 r/min，输入扭矩477 N·m，其运行时间占据工作时间的绝大部分，具有代表性，故选取此工况为研究对象。

图3 激励加载点位置

2.2 模态分析

齿轮箱的材料为铸钢，弹性模量为210 GPa，泊松比为0.3，密度为7 800 kg/m3。使用六节点的Solid185单元对齿轮箱的薄壁结构进行网格划分，网格尺寸为10 mm，共生成15 979个六面体单元如图4所示。其余结构采用四节点的SOLID285单元划分，共得到330 238个节点，1 257 477个单元。

图4 齿轮箱六面体网格模型

在有限元模型建立过程中，为方便加载在箱体5个轴承孔中心位置建立集中质量节点单元，并与轴承孔内壁表面节点建立刚性耦合关系，施加轴承动载荷时，直接加载至集中质量节点即可把激励施加到箱体。箱体的底部依靠12个螺栓的压紧力，使箱体的底面与基础接触，其只能沿着螺栓方向上下运动。因此本文采用COMBIN14弹簧单元来模拟箱体与基础间的连接关系，弹簧单元的下节点约束所有方向的自由度，弹簧单元的上节点放开竖直方向自由度并约束其他方向自由度，建立耦合和约束关系后的齿轮箱有限元模型如图5所示。

图5 齿轮箱有限元模型

使用Lanczos法对齿轮箱有限元模型进行模态分析，得到箱体的前21阶固有频率如表1所示。

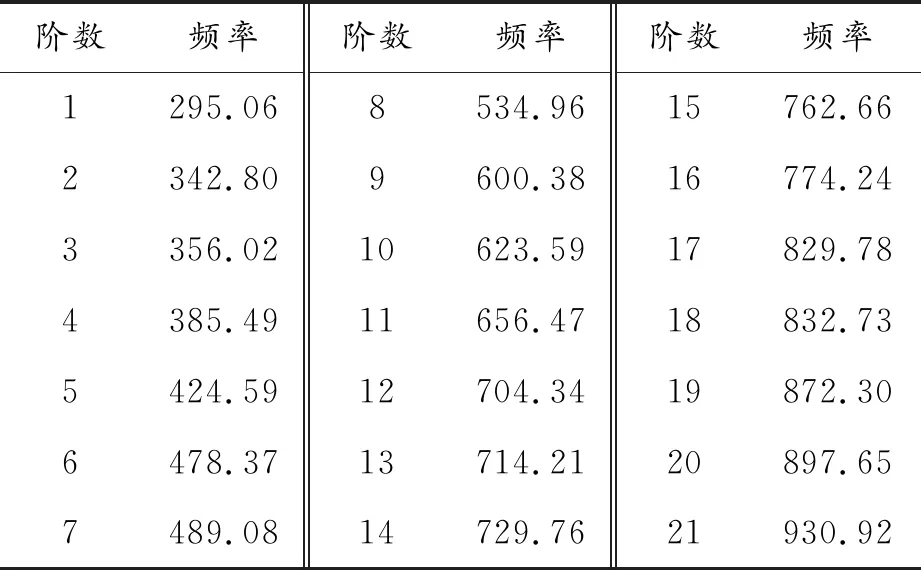
表1 齿轮箱前21阶固有频率 Hz

3 齿轮箱的振动响应分析

3.1 动载荷激励

在模态分析的基础上采用模态叠加法进行齿轮箱的振动响应计算，在5个加载点处施加如图6所示的轴承动载荷，该动载荷考虑了包括啮合刚度波动、制造和安装误差、啮合冲击等系统内部激励。载荷会通过轴传递至轴承座，将振动传递至齿轮箱体上，最终传递到箱体的机脚螺栓附近。因此，选择12个机脚螺栓孔的上节点作为振动响应测点来说明齿轮箱体结构的振动响应。齿轮箱12个机脚测点的位置分布及编号如图7所示。

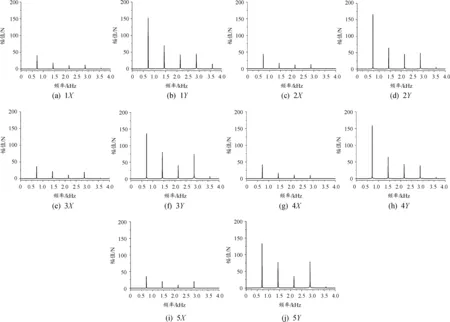
图6 5个加载点的动载荷频谱图

图7 机脚测点的位置分布

3.2 振动响应与谐响应分析

计算得到的12个机脚测点的Y向振动加速度级频谱图如图8。由图可知，12个机脚测点的振动加速度级均集中在啮合频率及其各阶倍频处，峰值均出现在2 870.88 Hz处。除此之外，图中还出现了近似阶梯状的线条，这是由于其余频率处的振动加速度均为极小值，导致换算为振动加速度级时出现了近似直线的情况，不过这些频率成分在振动响应中不占据主要地位。

图8 12个测点的Y向振动加速度级频谱图

如表2所示为齿轮箱12个机脚测点的Y向有效振动加速度级。由表可知，12个机脚测点的有效振动加速度级都在110 dB左右。通过降低机脚测点的振动加速度峰值，即可降低其有效振动加速度级，因此下一步单频激励谐响应分析和结构声强计算的目标频率为2 870.88 Hz。

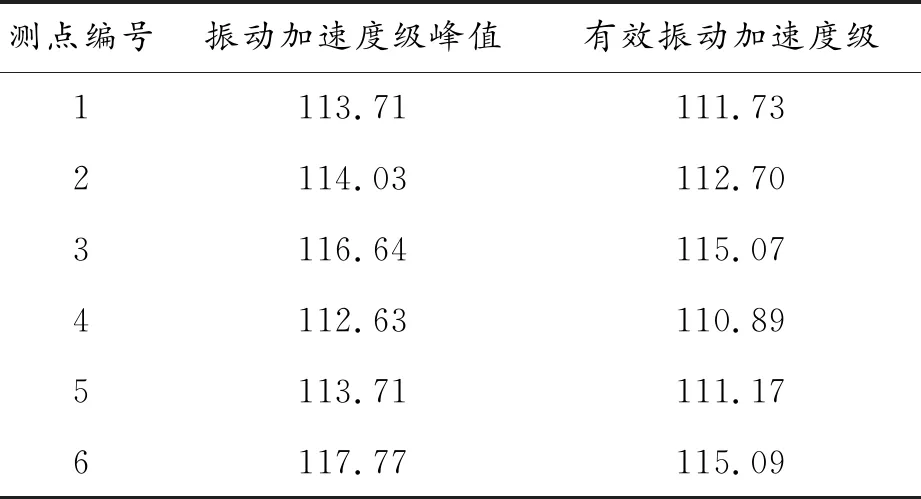
表2 齿轮箱12个测点的振动加速度级峰值和有效振动加速度 dB

通过在5个激励加载点施加2 870.89 Hz处的简谐激励，在模态分析的基础上进行单频激励下的谐响应分析，得到节点位移；并在激励频率处进行扩展，得到单元应力。计算得到的节点位移和单元应力可作为下一节结构声强计算和可视化的基础。

续表(表2)

4 齿轮箱的结构声强计算及可视化

使用ANSYS 参数化设计语言提取各单元的单元应力，组成单元的各节点位移，根据式(4)使用APDL计算各个单元X、Y、Z向的结构声强数值，并计算各个单元的结构声强幅值。通过DESOL命令将齿轮箱薄壁结构15 979个单元的单元应力值替换为单元结构声强幅值，查看这些单元的应力云图，即可得到目标频率2 870.88 Hz下齿轮箱薄壁结构的结构声强幅值云图，如图9所示。

由图9可知，齿轮箱薄壁结构的振动能量主要分布在箱体输出端盖的中间四块板，因此，下一步附加阻尼减振设计的目标区域为箱体输出端盖的中间四块板。

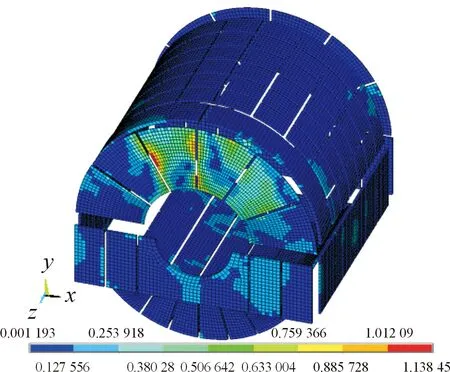
图9 目标频率2870.88Hz下齿轮箱薄壁结构的结构声强幅值云图

5 齿轮箱阻尼材料布局方案对比

5.1 齿轮箱局部附加阻尼的减振设计

由结构声强幅值云图可知，在目标频率2 870.88 Hz下，齿轮箱振动能量较大的区域为箱体输出端盖的中间四块板。因此对箱体进行局部附加阻尼处理，阻尼材料的附加区域为箱体输出端盖的中间四块板，阻尼材料为SA-3船用阻尼材料。齿轮箱局部附加阻尼材料后的几何模型如图10所示，通过计算可知阻尼材料的覆盖率为10%。

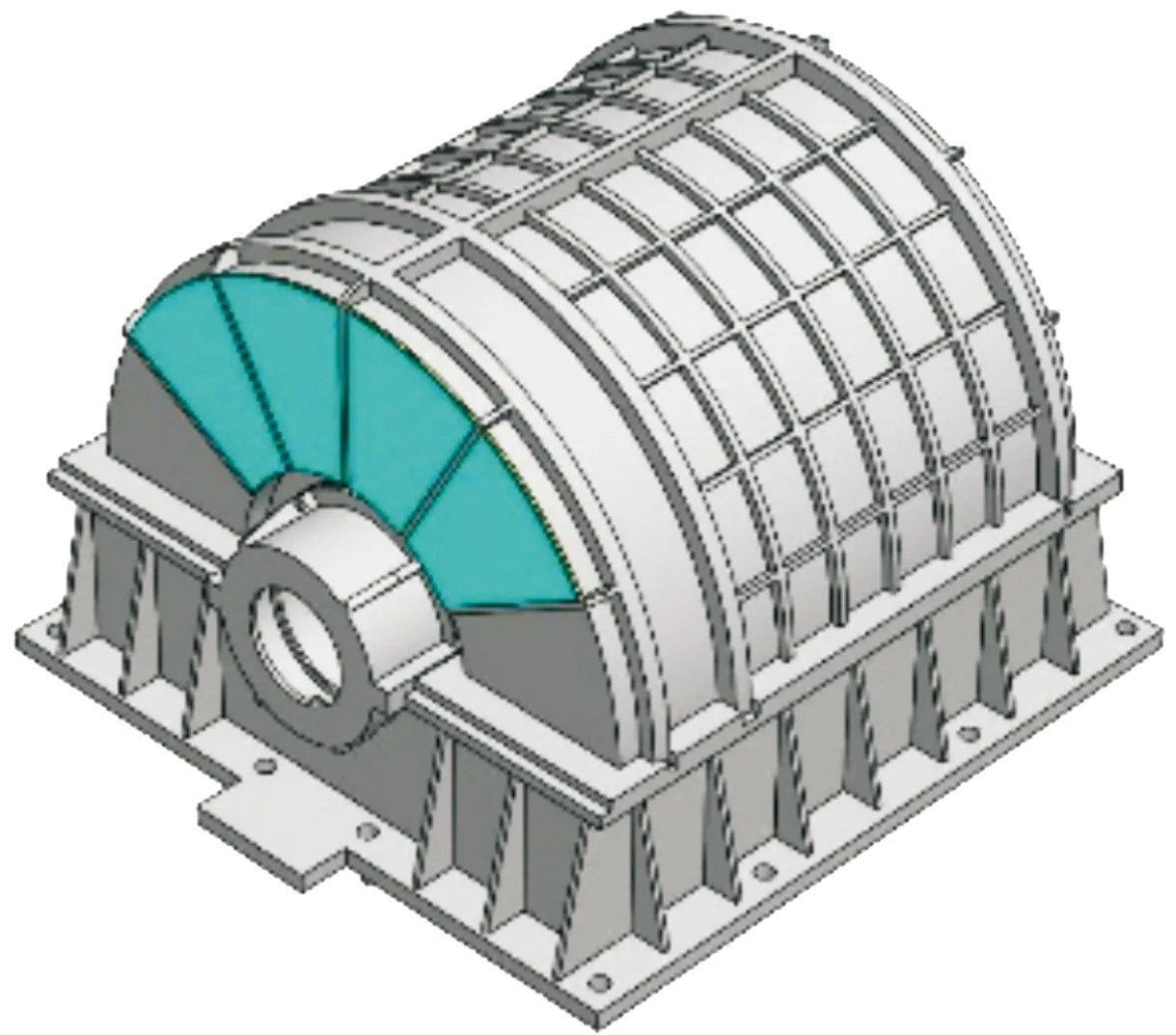
图10 局部附加阻尼材料后的齿轮箱几何模型

对齿轮箱局部附加阻尼处理后的齿轮箱进行模态分析，并求解各阶的模态应变能，根据式(5)计算各阶模态的损耗因子。

(5)

(6)

式中ξi为整体结构的第i阶模态阻尼比。

根据式(6)计算可得到各阶的模态阻尼比。通过计入各阶的模态阻尼比可求解附加阻尼材料后齿轮箱的振动响应。附加阻尼材料前后的齿轮箱机脚测点的有效振动加速度级及差值如表3所示。

表3 齿轮箱局部附加阻尼前后的12个测点的有效振动加速度级及差值 dB

由表3可知，经过局部附加阻尼材料处理后，12个机脚测点的有效振动加速度级均降低，其均值下降了2.69 dB，可证明基于结构声强可视化的齿轮箱局部附加阻尼减振方法的有效性。其中机脚测点5的有效振动加速度级下降得最多，因此，给出机脚测点5在啮合频率及倍频处的振动加速度级，如表4所示。

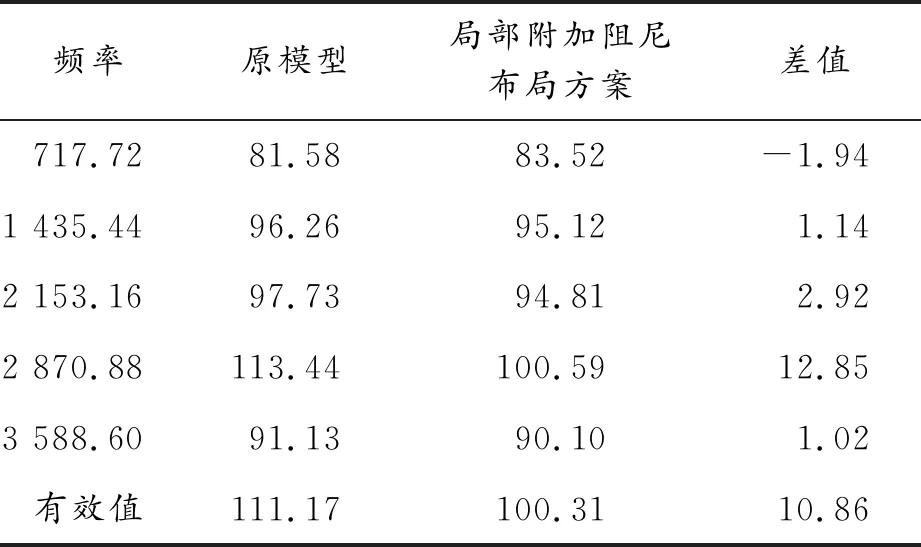
表4 齿轮箱局部附加阻尼前后的测点5在啮合频率及倍频处的振动加速度级 dB

由表4可知，齿轮箱局部附加阻尼材料后，机脚测点5在目标频率2 870.88 Hz处振动加速度级下降最多，达到了12.85 dB。通过降低机脚测点5在2 870.88 Hz处的振动加速度级峰值，其有效振动加速度级下降了10.86 dB,这点也符合预期通过降低振动加速度级峰值来降低有效振动加速度级的目标。

5.2 阻尼材料布局方案的结果对比

为了验证本文方法的先进性，将其与另一种常见的方案进行了对比，即齿轮箱薄壁结构的外表面100%覆盖阻尼材料。齿轮箱薄壁结构的外表面全局附加阻尼材料后的几何模型如图11所示。

图11 全局附加阻尼材料后的齿轮箱几何模型

表5所示为齿轮箱薄壁结构的外表面全局附加阻尼材料前后齿轮箱机脚测点的有效振动加速度级及差值。

表5 齿轮箱全局附加阻尼前后的12个测点的有效振动加速度级及差值 dB

由表5可知，经全局附加阻尼处理后，齿轮箱12个机脚测点的有效振动加速度级均值下降了1.33 dB，齿轮箱部分机脚测点的有效振动加速度级降低了，测点3、5、6、7、8、10、11、12的有效振动加速度级分别下降了0.36、1.71、9.60、5.52、3.20、1.15、5.77、1.81 dB；但是，部分机脚测点的有效振动加速度级反而升高了(其差值为负值)，如测点1、2、4、9的有效振动加速度级分别上升了0.27、0.56、4.67、7.71 dB。

表6所示为2种方案附加阻尼处理得到的齿轮箱机脚测点振动加速度级的降低值。与全局附加阻尼方案相比，局部附加阻尼方案虽然只有10%的阻尼材料覆盖率，但其12个机脚测点的有效振动加速度级均降低了，而且实现的减振量均值达到全局附加阻尼方案减振量均值的2倍。该结果表明全局附加阻尼方案中部分阻尼材料不仅没有参与结构耗能，反而增加了结构的质量和体积，同时证明了本文基于结构声强可视化的齿轮箱局部附加阻尼减振方法具有更高的材料利用率。因此，阻尼材料只有附加到合适的位置时，才会达到理想的耗能效果。

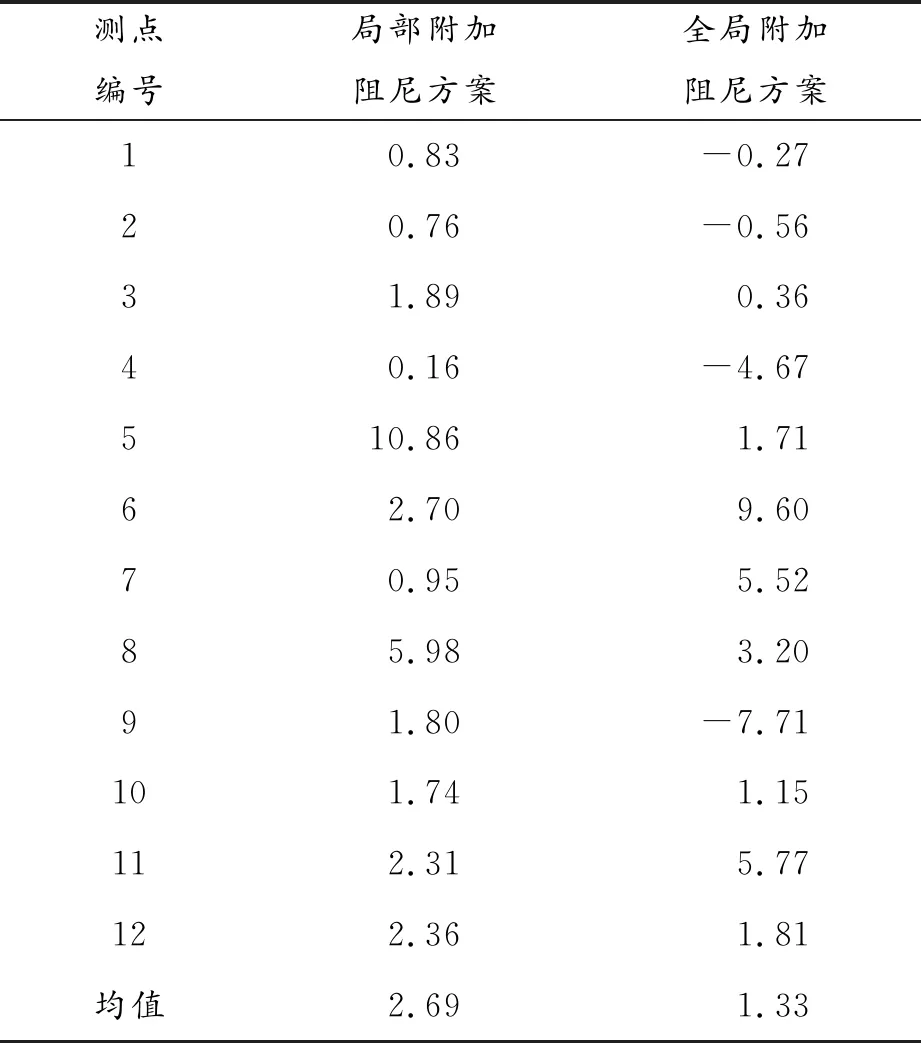
表6 局部附加阻尼方案与全局附加阻尼方案的减振结果对比 dB

6 结论

1) 通过ANSYS APDL实现结构声强可视化，得到结构声强幅值云图，可以确定振动能量大的区域，即阻尼材料附加的有效区域。

2) 通过对振动能量大的区域附加阻尼材料，使得算例齿轮箱体12个机脚测点的有效振动加速度级均有所降低，其均值下降2.69 dB，证明了基于结构声强可视化的齿轮箱局部附加阻尼减振方法的有效性。

3) 本文方法可有效降低测点的振动响应，减少阻尼材料的消耗，减轻结构的质量和体积，在工程应用中具有良好的应用价值。