孔隙压力升降条件下煤岩双孔隙渗透率模型研究

尧春洪，李波波,2,3，高 政，李建华，许 江

（1.贵州大学 矿业学院，贵州 贵阳 550025；2.贵州大学 喀斯特地区优势矿产资源高效利用国家地方联合工程实验室，贵州 贵阳 550025；3.贵州省非金属矿产资源综合利用重点实验室，贵州 贵阳 550025；4.重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044）

0 引 言

煤岩通常被认为是由多孔基质块体和裂隙组成的双重孔隙介质，孔隙和裂隙的性质直接影响煤岩气体吸附和运移特性[1]。渗透率是反映煤岩内气体流动的关键参数[2]，虽然裂隙渗透率比基质渗透率大几个数量级[3]，但是基质内气体流动过程也会对煤层瓦斯抽采率产生影响。因此，研究不同孔隙压力条件下基质渗透率和裂隙渗透率的演化规律十分重要。

在煤层瓦斯抽采过程中，煤岩渗透率受有效应力、孔隙压力、气体吸附/解吸特性、孔裂隙结构特征和滑脱效应等因素影响，为此，相关学者通过试验对这些机制展开研究。马如英等[4]开展覆压孔渗试验，认为有效应力变化是影响煤储层渗透性大小的重要因素。梁冰等[5]开展不同围压和孔隙压力条件下的解吸-渗流试验，得出煤岩渗透率随孔隙压力降低先减小后增大的结论。李立功等[6]开展核磁共振试验和渗流试验，发现滑脱效应与不同基质和裂隙的宽度有关系。为定量研究煤层瓦斯抽采过程中渗透率与孔隙和裂隙之间的关系，相关学者进行大量理论模型研究。ZHOU等[7]将裂隙体系作为渗流主要通道，建立裂隙渗透率模型，研究可变滑脱效应对渗透率的影响。CAO等[8]考虑有效压力、吸附和流动状态对气体渗透率的影响，基于孔隙弹性理论和流态理论建立相关渗透率模型。ZHU等[9]建立煤岩孔隙度和渗透率相结合的理论模型，但未探讨基质/裂隙孔隙度对煤岩渗透率的作用。LIU等[10]建立一种双渗透率模型，以表征基质渗透率和裂隙渗透率的演化过程。SI等[11]考虑吸附层的厚度，计算有效孔隙半径，并建立双孔隙渗透率模型，揭示基质与裂隙的相互作用机理。

综上所述，以往对煤岩渗透率研究多集中于孔隙压力单调变化条件下的基质/裂隙渗透率模型,关于气体先注入后排出的煤岩双孔隙渗流特性研究相对较少。拟在双孔隙弹性理论的基础上，结合滑脱效应对基质和裂隙中气体运移的影响，分别构建孔隙压力升高作用下的裂隙渗透率模型和考虑吸附层厚度的基质渗透率模型。并在此基础上，引入修正函数L（p）计算孔隙压力降低条件下的煤岩渗透率。通过试验数据对模型展开验证并分析讨论相关参数，为煤层瓦斯抽采提供理论支持。

1 煤岩双孔隙渗透率模型

1.1 基质孔隙度和渗透率

假设煤岩中的孔隙压力与基质、裂隙中的孔隙压力相等，则基质孔隙度φm[10]可表示为

（1）

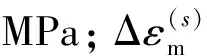
煤岩吸附瓦斯引起的应变增量[13]可表示为

（2）

式中：Δεs为煤岩吸附应变之差；ρc为煤岩密度，g/cm3；a、b为吸附常数，cm3/g；R为气体常数，J/（mol·K），取值为8.314 J/（mol·K）；T为温度，K，取T为303 K；V0为标准摩尔体积，约为22.4 L/mol；EA为煤岩吸附所导致的膨胀模量，MPa；p为煤岩孔隙压力，MPa；p0为煤岩初始孔隙压力，MPa，取值为0。

由于基质吸附应变和基质孔隙吸附应变难以通过试验测量，因此可以采用以下公式计算得到[10]

（3）

（4）

式中：f1和f2为无量纲常数。

将式（2）—式（4）代入式（1）中可得

（5）

吸附气体进入煤岩后其内部孔隙表面的范德华力被削弱从而产生膨胀能，使煤岩基质宏观上表现出膨胀变形[14]。煤岩基质孔隙壁上的吸附层厚度增加，这将降低平均孔隙半径和基质渗透率。基质平均孔隙半径可根据式（5）表示为[8]

（6）

式中：r为基质平均孔隙半径，m；r0为基质初始平均孔隙半径，m。

结合式（2），煤岩基质吸附层厚度[9]可以表示为

（7）

式中：dads为基质吸附层厚度，m；Dgas为吸附气体分子的直径，m。

气体流动时的基质有效孔隙半径为

re=r-dads

（8）

式中：re为基质有效孔隙半径，m。

根据文献[15]的研究报道，煤岩基质渗透率模型可以描述为

（9）

1.2 裂隙孔隙度和渗透率

煤岩体积V、基质体积Vm和裂隙体积Vf的关系可以被表示为V=Vm+Vf，根据裂隙孔隙度的定义可得

（10）

式中：φf为裂隙孔隙度；φf0为初始裂隙孔隙度；V0为初始煤岩体积，m3；ΔV为煤岩体积之差，m3；ΔVm为基质体积之差，m3；Vm0为初始基质体积，m3。

根据孔隙度的定义，可推导出以下表达式[17]：

（11）

式中：Δφf为裂隙孔隙度之差。

煤岩体积应变在考虑有效应力和煤岩吸附膨胀等一系列作用后可被表示为[10]

（12）

式中：Δεv为煤岩体积应变之差；K为煤岩体积模量，K=E/[3（1-2ν）]，MPa，其中E为弹性模量，MPa；ν为泊松比；α为煤岩Biot系数，α=1-K/Ks，Ks为基质体积模量，MPa，由于K≤Ks，通常将α取定值为1。

由式（12）可得

（13）

将式（11）和式（13）代入式（10）中可得

（14）

裂隙孔隙度与裂隙渗透率之间的关系可用立方定律表示为

（15）

式中：kf为煤岩裂隙渗透率，10-3μm2；kf0为煤岩裂隙初始渗透率，10-3μm2。

1.3 煤岩渗透率

孔隙压力较小时滑脱效应显著，考虑滑脱效应的煤岩总渗透率k[18]可以表示为

（16）

式中：ka为克氏渗透率，10-3μm2；B为滑脱因子，MPa。

在一定温度条件下，滑脱因子的大小与气体类型、煤岩孔隙和裂隙的宽度有关[6]，因此可以分别建立考虑不同滑脱因子的基质渗透率和裂隙渗透率。由式（9）、式（15）和式（16）可得

（17）

（18）

式中：B1、B2分别为基质孔隙和裂隙中的滑脱因子，MPa。

孔隙压力升高时的煤岩总渗透率可以定义为

（19）

将降压和升压试验过程中的煤岩总渗透率比值定义为修正因子L，然后通过修正因子L与孔隙压力的关系得到相关修正函数L（p）。孔隙压力降低时的煤岩总渗透率模型可表示为

ku=kL（p）

（20）

式中：ku为孔隙压力降低时的渗透率，10-3μm2；L（p）为修正函数。

2 试验方法

2.1 试样及试验装置

试验所用煤样取自重庆松藻煤矿K2煤层，取样深度为200～300 m，煤样的水分、灰分、挥发分和固定碳分别为1.53%、37.20%、11.36%和49.91 %，将所采无烟煤制备成ø50 mm×100 mm的型煤试件。由于松藻煤层较为松软，很难在现场取到大块原煤进行试验，根据文献[19]的试验结论，型煤可以代替原煤在实验室进行试验。试验装置为含瓦斯煤热-流-固耦合三轴伺服渗流装置，可进行不同轴压、围压及不同孔隙压力条件下的煤岩力学与渗流特性试验研究[20]。

2.2 试验方案

试验选用CH4作为试验气体。根据煤样赋存实际状况，在实验室内设置相关力学条件。在轴压和围压控制为2.0、4.0、6.0、8.0 MPa下，分别进行孔隙压力升高（0.20→0.35→0.50→0.65→0.80→0.95→1.10→1.30→1.55→1.80 MPa）和降低的渗流试验。将试验所得的瓦斯流量代入达西定律公式计算不同轴压、围压条件下煤岩总渗透率。具体试验步骤参照文献[12]。

3 结果分析及模型验证

3.1 煤岩渗透率演化规律

1）升压过程的煤岩基质和裂隙渗透特性分析，吸附试验数据取自文献[13]，将模型相关参数分别代入式（17）可得各平均应力下的基质渗透率km随孔隙压力变化的规律曲线，如图1所示。

从图1可看出，当平均应力恒定时，km随孔隙压力增大有先急剧减小后缓慢减小的趋势。分析可知，在本试验的孔隙压力升高范围内，吸附膨胀效应对km的抑制作用始终大于有效应力减小对km增长起到的有益作用。当孔隙压力加载到一定值时，吸附量逐渐达到饱和，此时km降低态势转向平缓发展。由于裂隙渗透率kf比基质渗透率km高几个数量级，故裂隙渗透率kf与煤岩总渗透率变化趋势较为一致。

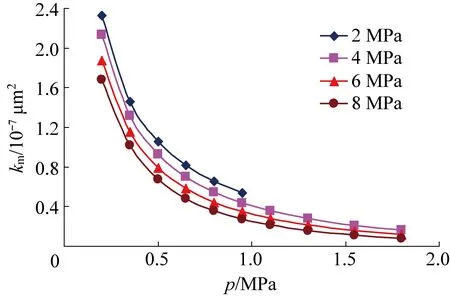
图1 不同平均应力下基质渗透率随孔隙压力变化规律Fig.1 Change of matrix permeability with pore pressure under different mean stresses

图2 煤岩总渗透率随孔隙压力变化规律Fig.2 Change of total coal permeability with pore pressure

2）升压过程的煤岩总渗透特性分析，将模型相关参数分别代入式（19）中，可得升压过程中的煤岩总渗透率变化规律曲线，以平均应力σ=6.0 MPa时煤岩总渗透率随孔隙压力变化规律为例，如图2所示。从图2可看出，模型曲线与试验曲线有较高的匹配度。当平均应力一定时，煤岩总渗透率随孔隙压力增大呈“V”型变化，即先减小后增大并存在明显的拐点。这主要由以下原因共同造成：①孔隙压力升高导致煤岩裂隙楔开程度增大，其有利于渗透率增大；②平均应力恒定条件下，孔隙压力升高导致有效应力降低，对煤岩孔裂隙压缩限制作用相对减弱，对渗透率起促进作用；③煤岩不断吸附膨胀导致吸附层加厚，有效渗流通道受限，对渗透率起抑制作用；④低压滑脱效应显著，滑脱效应随孔隙压力增大逐渐减弱，对渗透率起抑制作用。其中，起反向作用的因素在拐点前占据主导地位，起正向作用的因素在拐点后占据主导地位。

3）降压过程的煤岩总渗透特性分析，通过对试验数据进行分析，发现修正函数L（p）随孔隙压力增大呈近似对数增长，修正函数L（p）可被表示为

L（p）=cln（p）+d

（21）

式中：c，d均为敏感性系数。

将升压阶段平均应力σ=6.0 MPa时的煤岩总渗透率计算值代入式（20）和式（21）可得对应降压阶段的总渗透率值（图2）。从图2可看出，当平均应力一定时，煤岩总渗透率随孔隙压力减小呈“V”型变化趋势，并存在明显的拐点。造成这种现象的原因与升压过程的渗透率变化原因相对应。同时，煤岩渗透率在经历孔隙压力升降后并未回归原先对应位置。考虑到孔隙压力是影响煤岩渗流的主要因素，因此研究孔隙压力升降条件下的煤岩渗透率变化规律，对于煤层注气开采和瓦斯灾害防治具有重要意义。

3.2 敏感性系数分析与讨论

为进一步探究修正函数L（p）对降压过程中渗透率的影响规律，分别在敏感性系数c、d试验范围内选取部分恒定值，绘制不同c和d下的煤岩总渗透率曲线（图3）。

图3 修正函数L（p）的系数敏感性研究Fig.3 Study on coefficient sensitivity of modified function L（p）

图3表明，在孔隙压力降低至拐点后，c值大的渗透率曲线明显低于c值小的渗透率曲线。分析可知，当平均应力一定时，在孔隙压力减小至拐点后滑脱效应不断增强，煤岩总渗透率逐渐增大且速度变快，这表明系数c可能与滑脱效应有关。系数d对煤岩总渗透率大小影响较为明显，当孔隙压力一定时，d值较大的渗透率曲线整体高于d值较小的渗透率曲线，即d值和渗透率之间可能存在正向关系。

4 结 论

1）当平均应力恒定时，基质渗透率随孔隙压力增大而减小，且减小速率逐渐降低，这一过程主要与有效应力、吸附膨胀效应有关。由于裂隙渗透率比基质渗透率大几个数量级，裂隙渗透率与煤岩总渗透率具有较为接近的变化趋势。

2）当平均应力恒定时，煤岩总渗透率随孔隙压力增大呈先减小后增大的变化趋势，并存在明显的拐点，降压过程渗透率变化趋势与之相对应。煤岩总渗透率在经历升压后再卸压表现出明显的迟滞效应。

3）在新建升压阶段的双孔隙渗透率模型基础上，引入修正函数L（p）建立降压阶段的总渗透率模型。通过试验表明，新建渗透率模型能较为精确表征孔隙压力升降控制下的煤岩渗透率演化特征。

4）敏感性系数c可能与滑脱效应有关，在孔隙压力降低至拐点后，滑脱效应越发增强，c越小，渗透率越大；敏感性系数d对渗透率大小影响较为明显，2者间可能呈正向相关关系。