基于特征点与改进ICP的点云配准方法
黄际玮,陆安江
(贵州大学大数据与信息工程学院,贵阳 550025)
1 引言
随着三维激光扫描技术在文物保护、三维重建、无损检测等领域的快速发展,点云配准[1]在三维图像领域得到广泛应用。由于仪器视角与物体自身遮挡等因素的限制,需要从多个站点才能获取物体的全部信息,通过点云配准技术可以寻找出最优旋转平移矩阵,使得不同视角下的物体能够变换到同一坐标系下[2],从而得到完整的点云数据。目前已有大量的学者对点云配准进行研究,其中Besl等人[3]提出的迭代最近点(Iterative Closest Point,ICP)算法应用最为广泛,但要求点云的初始位置较好,且收敛速度较慢。针对这些问题,宋成航等人[4]利用向量夹角提取特征点后通过快速点特征直方图(Fast Point Feature Histograms,FPFH)描述特征点,并在ICP算法中加入KD-tree完成最终配准;李慧慧等[5]在ICP算法中利用二次搜索求出最近距离,提高传统ICP算法的效率;李为民等[6]在主成分分析法(Principal Component Analysis,PCA)的基础上完成初始配准,但PCA算法要求待配准点云有较高的重叠度;荆路等人[7]则是利用SIFT算法提取特征点并结合SACIA算法完成初始配准,提高了配准精度,但SIFT算法耗时较长。针对上述仍然存在的问题,在此提出一种基于特征点与改进ICP的点云配准方法。
2 算法原理
本算法采用的方法是在粗配准阶段使用ISS算法从下采样点云中提取特征点,结合采样一致性算法完成初始配准,在精配准阶段加入法向量夹角约束剔除误配点,代替传统ICP算法中将全部点云参与计算,以此提高算法速度与精度。
2.1 关键点提取算法
算法总体步骤如图1所示。对原始点云进行下采样后,通过ISS算法从采样点中提取特征点并用FPFH进行特征描述;利用SAC-IA算法对原始点云进行初始配准,最终采用法向量约束的改进ICP算法完成精细配准。
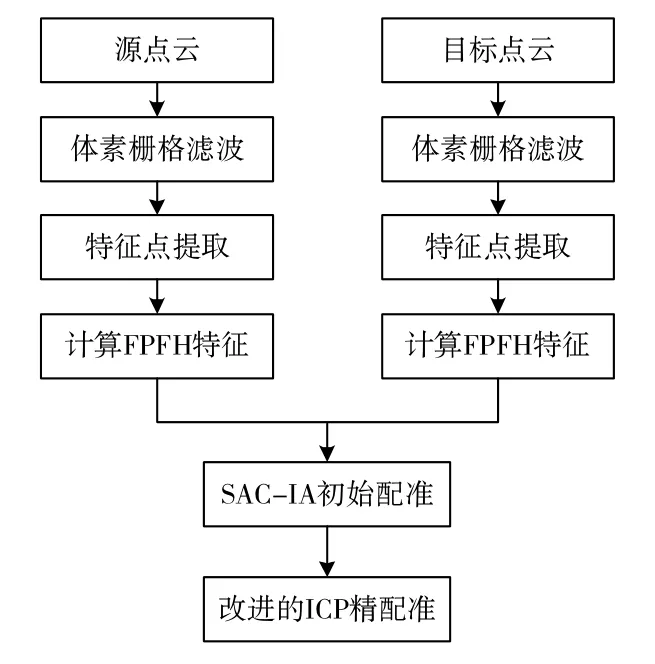
图1 算法总体框架
在点云空间中,一些点具有较为明显的几何特征且具有尺度不变性,这些点通常称为特征点。内部形态描述子(Intrinsic Shape Signatures,ISS)算法[8]可以对局部信息进行有效提取,其原理如下:
1)对点云P中每个点pi建立一个局部坐标系,并设置搜索半径ri;
2)以pi为中心,搜索其半径ri内的k个邻域点,根据中心点与邻域点的距离计算出每个邻域点的权值wij如下:
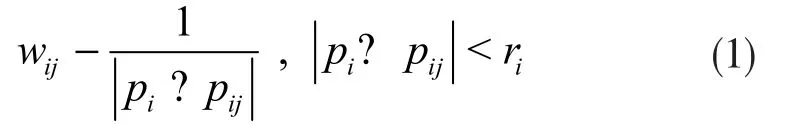
3)构建pi与pij的协方差矩阵cov(pi):
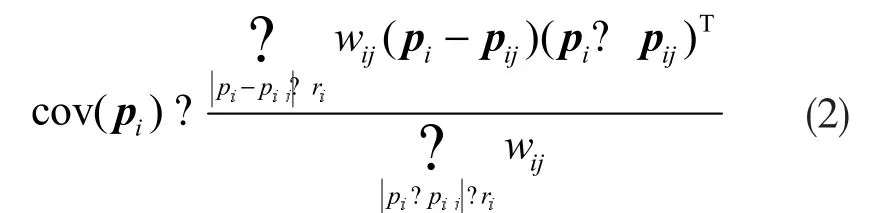
4)由协方差矩阵求出对应特征值{λi1,λi2,λi2},其中λi1<λi2<λi3;
5)分别设置两个阈值ε1与ε2,若满足λi2/λi1≤ε1且λi1/λi2≤ε2,则该点可视为特征点。
2.2 FPFH特征描述子
快速点特征直方图(FPFH)描述子[9]是一种局部特征描述子,它以直方图的形式表示局部邻域内点云间的特征,如图2所示。以查询点pq为圆心,r为半径搜索邻域点,并分别计算其法向量,通过角度三元组(α,φ,θ)表示查询点与邻域点之间的关系,得到简化的点特征直方图(Simplified Point Feature Histgram,SPFH)特征,如图3所示。
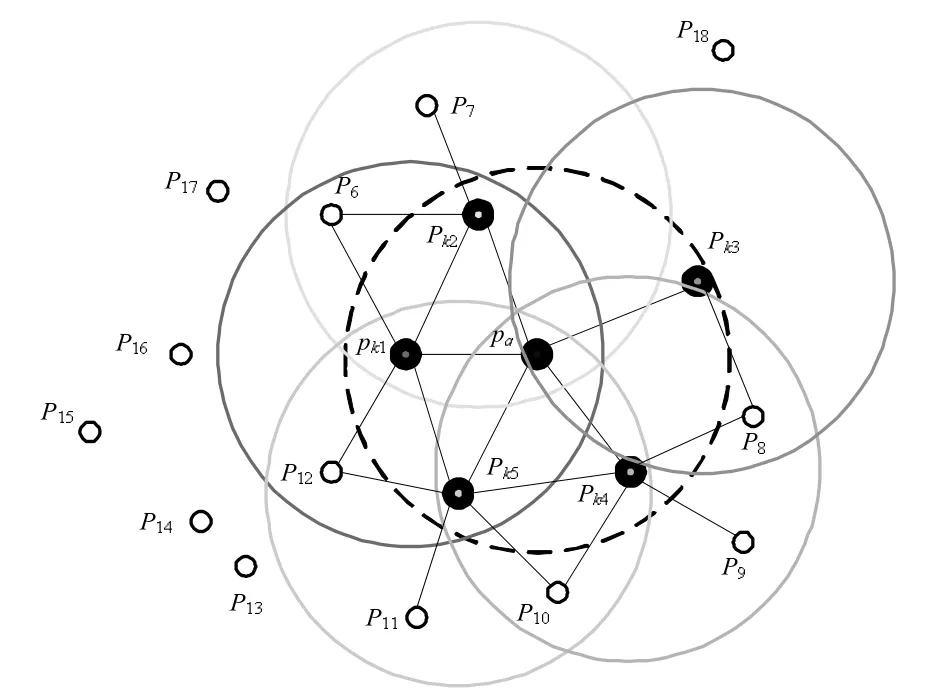
图2 FPFH邻域范围示意图
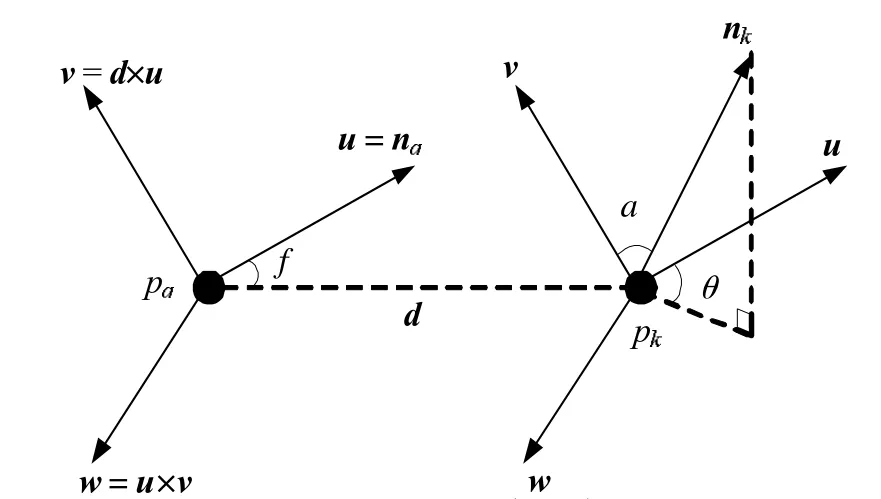
图3 SPFH局部坐标系
图中的nq、nk分别为pq、pk的法向量,d为pq、pk的距离向量,可得出:
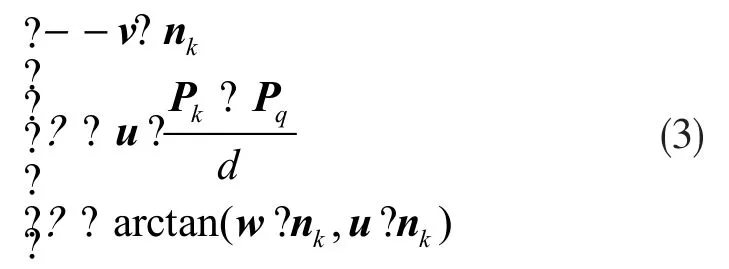
以此对查询点ps的邻域进行更新,通过所有邻域点的SPFH特征计算得到ps的FPFH特征,如下式:
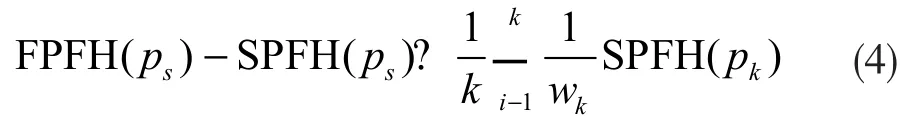
其中权重wk表示查询点ps与其邻域点pk的欧氏距离,k为邻域点数量。
2.3 点云粗配准
在点云配准中,粗配准结果好坏直接影响到后续精配准效果。采用采样一致性(Sample Consensus Initial Aligment,SAC-IA)算法[10]是一种常用的粗配准算法,具体步骤如下:
1)在源点云P中选取x个不同的采样点并设置距离阈值wd,以保证采样点间具有不同的FPFH特征;
2)在目标点云中寻找具有源点云采样点相似FPFH特性的点作为对应点;
3)通过对应点之间的位置关系计算出旋转平移矩阵,并用Huber函数判定是否为最佳变换,记为其中:
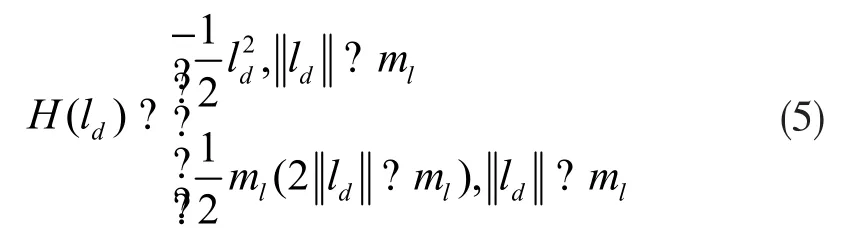
式中ml为设定值,ld为第d组对应点变换后的误差。重复上述步骤,使得误差函数最小的矩阵为最佳变换矩阵。
2.4 点云精配准
经粗配准后,两片点云已经大致对齐。为进一步减小误差,需要对点云进行精细配准。ICP算法是一种经典的点云配准方法,其原理[11]为:对于源点P云中的点pi,以欧氏距离为约束寻找目标点云Q中的对应点qi,通过对应点计算旋转平移矩阵R和T使得误差函数最小。误差函数定义为:
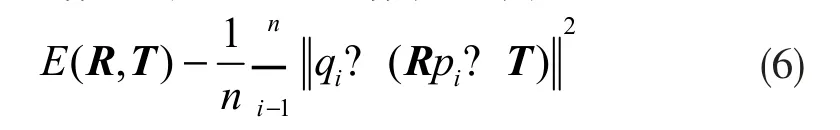
由此方式让所有的点都参与了计算,但其中的一些冗余点会导致计算速度拖慢,因此,在ICP配准过程中,设计加入法向量约束,设置法向量夹角阈值剔除误配点,以提高算法效率。具体步骤如下:
1)粗配准后源点云特征点集合为P',目标点云的特征点集和为Q',分别计算出每个点的法向量;
2)对P'中的每个点在Q'中查找对应的欧氏距离最近的点,记为点对N,然后设置法向量阈值fθ,若N的法向量夹角小于阈值,保留该点对,否则视为误配点,将其剔除,剔除误配点后的点对记为N';
3)根据N'使用SVD分解法计算变换矩阵(R,T),并根据误差函数E(R,T)求出最优的变换矩阵。
3 实验结果与分析
实验选用斯坦福数据集中不同角度的“兔”(Bunny)与“龙”(Dragon)点云作为配准对象。实验运行环境选取Visul Studio 2017+PCL(点云库)1.8.1,Windows操作系统,CPU为AMD Ryzen 5-4600H,16.00G内存。采用均方根误差(RMSE)来描述最终配准结果,定义为:

其中pj与qj分别表示源点云与目标点云中的对应点,n表示对应点数量。
原始点云中Bunny模型的点云的数量为40256与40097,Dragon模型的点云数量为41841与34836,如图4所示。
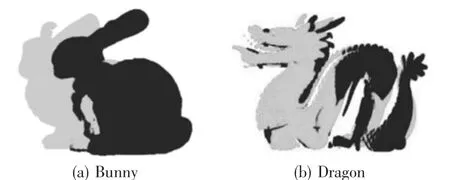
图4 原始点云位置
首先使用体素栅格对原始点云下采样,体素栅格边长设置为0.001m,然后进行特征点提取。其中各阶段的点云数量如图5所示。

图5 不同阶段点云数量
由图中可知,相对于原始点云,提取出的关键点数量减少了90%以上,通过这种方法可以在保留原始点云大部分特征的同时有效地提高后续的配准速度。最终提取出的特征点如图6所示。
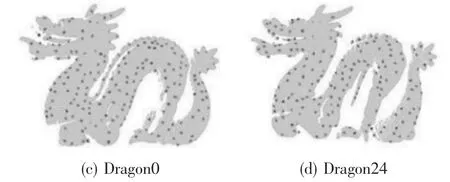
图6 点云中关键点提取
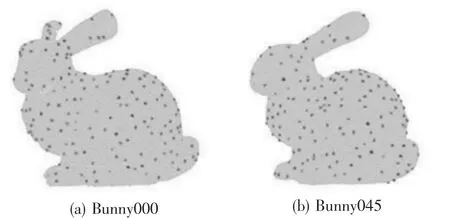
特征点分布于点云中凹凸性较强的位置,这些点更能代表点云的特征。提取出特征点之后,对特征点进行FPFH描述,并用SAC-IA算法对点云进行初始配准,最后结合法向量约束的ICP算法完成精细配准。配准效果如图7所示。
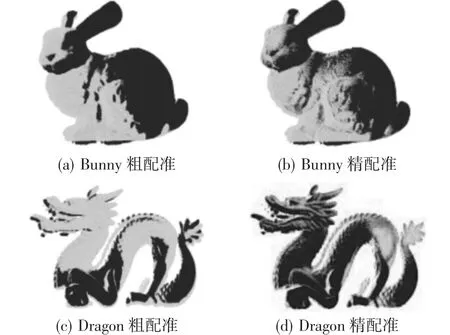
图7 本算法配准结果
可以看到,经过粗配准后,两点云的位置已经大致重合,但在一些细节处,如Bunny点云的背部和Dragon点云的尾部依然还存在误差;经过精细配准之后,两片点云的位置得到更好地校对。在配准过程中的配准误差与配准耗时如表1所示。

表1 本算法配准误差与耗时
本算法与ICP、4PCS+ICP、SAC-IA+ICP各算法的对比结果如表2所示。其中,本算法配准误差延用表1,配准耗时则为表1粗配准与精配准耗时之和。
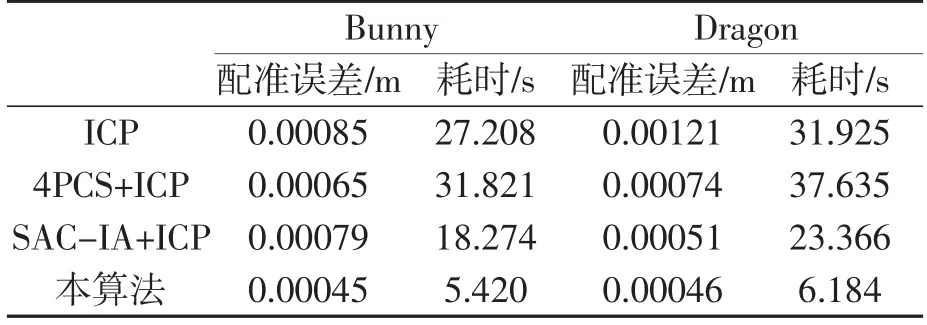
表2 不同算法对比
从对比结果可知,相较于其他现有算法,本研究提出的算法能够更好地实现点云配准。
4 结束语
基于特征点与改进ICP的点云配准方法,对于解决传统ICP算法中存在的问题,发挥出了良好的效果。初始配准阶段的ISS算法提取特征点与FPFH特征描述,后续的SAC-IA算法对原始点云的粗配准,以及最终在ICP算法中引入法向量约束剔除误配点对,都成功实现了对配准效果的优化。实验结果符合理论预期。相较于原始ICP、SAC-IA+ICP与4PCS+ICP各算法,本算法能够实现更高的配准精度与速度,具有很高的实际应用价值。

