染色机助剂智能配送系统的构建及实践

张福沐， 刘端武， 胡跃明

(1.华南理工大学 自动化科学与工程学院， 广东 广州 510640； 2.佛山市南海天富科技有限公司， 广东 佛山 528222)

染色是织物生产过程中的重要环节，由于织物的用量巨大，在染色环节消耗的材料、能源和人力资源都较大[1]，对此生产环节进行技术革新，可达到显著的经济效益和社会效益。

助剂的定量配送是染色时的一个重要步骤，染厂助剂配送的方式主要有3种：第1种是手工称量和手工配送；第2种是自动称量和手工配送；第3种是采用设备自动计量和配送。随着社会经济和技术的发展，第1种方式正在快速减少，第2种方式也在逐步减少，第3种方式逐渐成为主流配送方式。目前，国际上主要的助剂配送系统厂家有意大利的ColourServic公司、Lawer公司[2]和瑞士的Benninger公司，国内也有很多公司生产助剂配送系统，国内外的助剂配送系统均使用可编程逻辑控制器(PLC)控制，实现了自动计量和自动配送。

有些学者针对染色机助剂配送进行了研究，例如：文献[3]提出了一种基于变频控制的多流量调节控制配送精度的方法，基于液体为标准液体，忽略了各种助剂的流动性不同和各落料点管道阻力不同的影响；文献[4]提出了一种用于助剂称量的减小误差学习方法，使用负反馈作用于下一次的计量，这种方法同样也忽略了不同助剂流动性不一致的特征。为此，本文对影响助剂配送精度的多种因素进行分析，采用多层神经网络模型拟合配送因素的影响，对配送时的预停值进行预测，并对此进行了实验验证，以期为提高助剂配送精度提供新思路。

1 系统描述与问题提出

染色机助剂配送系统的结构如图1所示。助剂储存罐1用于存储待配送的助剂；助剂配送阀2是助剂配送的开关；冲洗水阀3用于在助剂配送阀门关闭后，打开水将残留在管道内的助剂冲到染色机料缸里；配送转子泵4用于将助剂或水在管道内向前推送；流量计5用于计量配送的助剂量和冲洗的水量；落料阀6用于控制助剂和水落到哪一台染色机料缸；染色机料缸7为助剂配送的目标料缸。

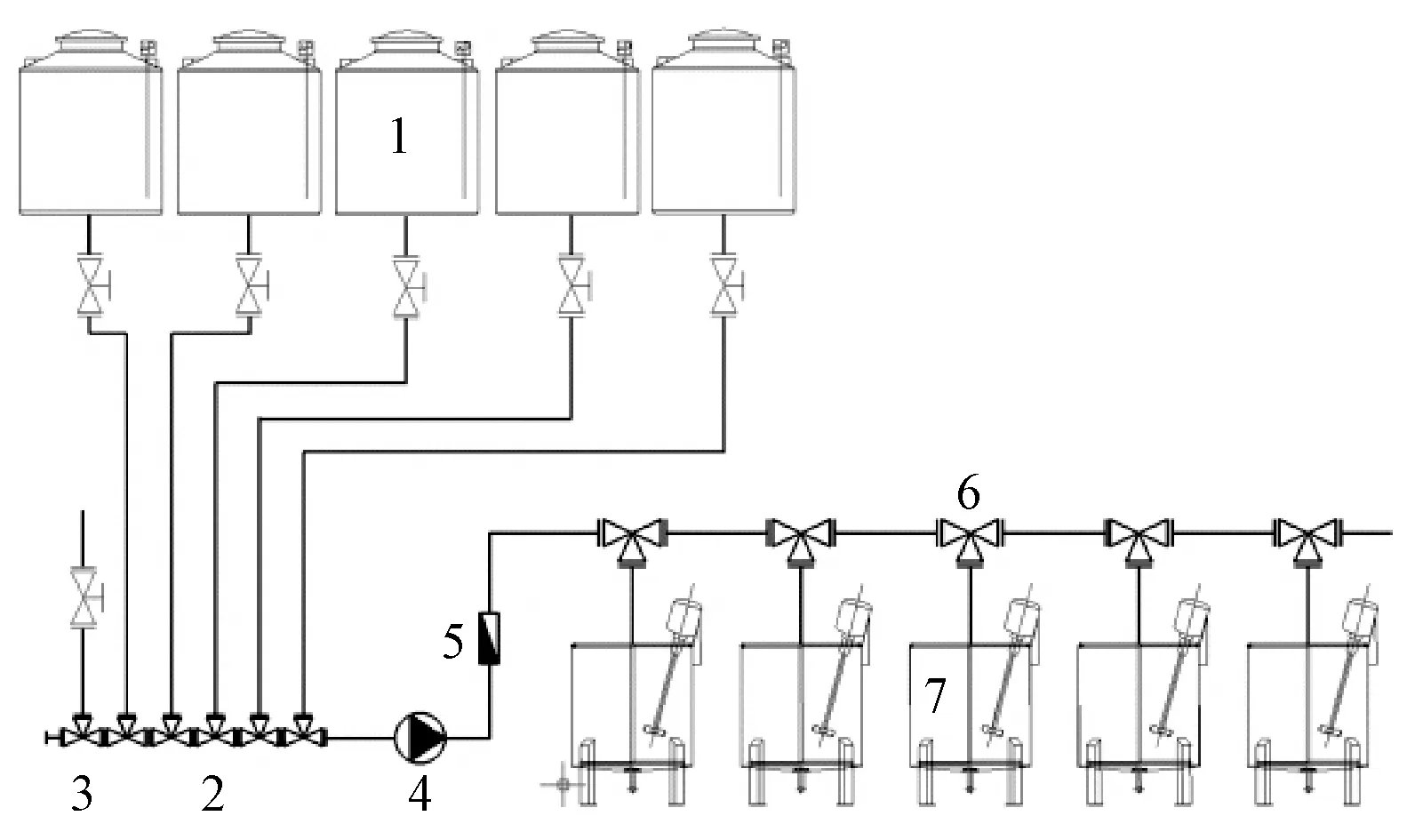
图1 染色机助剂配送系统结构图Fig.1 Structure diagram of chemical distribution system of dyeing machine

助剂配送时，在转子泵转动推力的作用下，助剂储存罐中的助剂通过管道流到相应的染色机料缸，助剂的流动过程是：助剂储存罐→管道→助剂配送阀→管道→转子泵→管道→流量计→管道→落料阀→管道→染色机料缸。

在染色机助剂配送过程中，当配送量到达，关闭阀门时，由于PLC扫描周期、继电器动作时间、电磁阀切换过程时间和配送阀门关闭过程时间的累加影响，从PLC发出关闭信号到阀门完全关闭，总共约有几百毫秒的时间。图2是在配送阀门关闭时刻开始，管道内流量与时间的关系图。

图2 关闭配送阀门时流量与时间的关系Fig.2 Relationship between flow rate and time when closing distribution valve

图2中T1表示PLC的扫描、运算和刷新输出时间，为5～20 ms；T2表示继电器的吸合时间，为5～10 ms；T3表示电磁阀阀芯换向时间，为10～50 ms；T4表示助剂配送阀关闭过程时间，为200～500 ms。从开始关闭配送阀门至阀门完全关闭所流过流量计的体积为

(1)

式中：Q(t)为流量关于时间的函数；Vvolume为T1+T2+T3+T4时间段流过流量计的总体积[5]，mL。

管道内液体流量与直径、流速的关系为

(2)

式中：D为管道内径,cm；V(t)为流速关于时间的函数。

由于流量计在计量时容易受到瞬时干扰的作用，导致瞬时速度变化较大[6]。为了抑制瞬时干扰对计量的影响，流量计采用在一小段时间内取流量平均值再输出的算法，这使得在某一时刻流量计输出的脉冲实际上是上一时间段至当前时间的平均脉冲，导致PLC接收到的累积脉冲换算体积比实际流过计量值的体积值少。图3示出流量计滞后输出流量的曲线图。

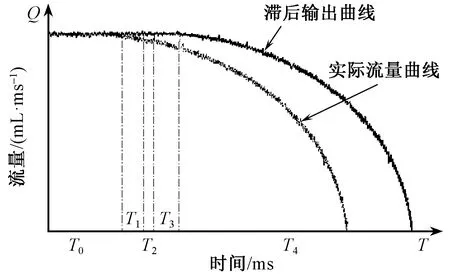
图3 流量计滞后输出流量的曲线图Fig.3 Graph of delay output flow of flowmeter

如图3所示，实际流过流量计的流量曲线与流量计滞后输出的流量曲线之间差了一个滞后时间长度T0，因此，开始关闭配送阀门至计量结束接收到的流量计所发出的总体积，是将式(2)代入式(1),再加上T0时间的体积，得到式(3)：

(3)

式中：T0为时间长度，等于流量计在一小段时间内取流量平均值再输出的时间长度，ms；Vtotal为关闭配送阀门后PLC系统统计的实时累积流量，mL；在配送过程中，Vtotal比Vvolume总是多了T0时间段的累积流量。

在PLC系统检测到符合关闭配送阀门的条件至计量结束这段时间内，不同助剂的黏度和流动性、不同落料口的配送管道长度、配送泵的运行频率大小等因素影响流速V(t)；PLC扫描周期影响T1、继电器吸合时间影响T2、电磁阀动作时间影响T3、压缩气的压强、配送阀轴向摩擦力等因素影响T4，从式(3)看，这些因素都会导致配送阀门关闭时流经阀门的助剂的体积Vtotal发生变化，综合影响着助剂系统的配送精度。

当配送完一种助剂时，系统送出少量的水冲洗流量计和管道，但是冲洗的水量不大，因为染色机料缸的容积不大，无法容纳大量的水，并且过多的水会导致料缸里的助剂浓度降低。这种多种助剂共用流量计配送的方式，不同助剂的黏度和电导率差异很大，在用少量水冲洗管道内的助剂后，还有少量上一次的助剂残留在管道、管道接头和流量计内壁。若接下来配送的助剂电导率与上一种助剂的电导率相差较大，流量计在计量时瞬时流速会跳动比较大，通过流速来评估预停值的偏差会比较大。

助剂配送系统受助剂黏度、流动性、管道阻力、配送泵频率、配送阀关闭时间、PLC扫描周期、继电器吸合时间、电磁阀动作时间等多种因素的影响，是一种大惯性和强滞后系统。如果要实现高效配送，需加大流量Q(t)，则需要加大管道直径或者加大流速V(t)；如果要实现高精度配送，需减小流量Q(t)，则需要减小管道直径或降低流速V(t)。在同一条配送支路里，管道的直径是固定的，无法变大和变小，只能是调整配送速度，如果要提高效率，则需要加大配送速度，但会导致配送精度下降。要实现助剂的高效、高精度配送，牵涉的条件很多，是一个非确定性多项式难解问题。

目前，助剂配送的精度控制需要技术人员多次进行配送测试，根据测试值调节助剂配送的预停值。由于助剂配送系统通常包含几十种助剂和几十台染缸，如果将这些条件一对一组合，将会有几千种，根据这些组合进行配送测试和调节配送预停值的工作量非常大；再者，系统配送的助剂有些是强酸、强碱或高腐蚀性溶液，调试时如果直接排掉，对环境造成非常大的危害；如果用容器装起来倒回储存罐，转运和清理过程容易沾到操作者的皮肤，对人体造成伤害。当前，染色机助剂配送系统调试时，通常的做法是用水做配送精度测试，根据不同的配送支路，设置不同的预停值，测试时直接把水排掉。这种简化的设置方法虽然可执行性较好，但是没有考虑助剂品种、落料点、配送泵的运行频率、压缩气压强等因素的影响，因而实际运行时配送精度较差。为了保证实际配送量达到定单所需的配送量，常常把预停值调到偏小，因而实际配送时一般实送量偏多，造成浪费，多余的助剂在染色时不能充分利用，染色完成后排到排污管，增加了污水处理的负担。基于目前存在的这些问题，急需研究一种更高精度、更智能化的染色机助剂配送系统。

2 解决方案的提出

针对助剂配送的误差问题，提取1 000次染色机助剂配送系统的配送数据进行分析。

助剂编号与配送误差的关系如图4所示。可以看出，不同助剂在配送时的误差有一定的规律，它们的误差分布中心是不同的，助剂编号是影响配送误差的一个因素。

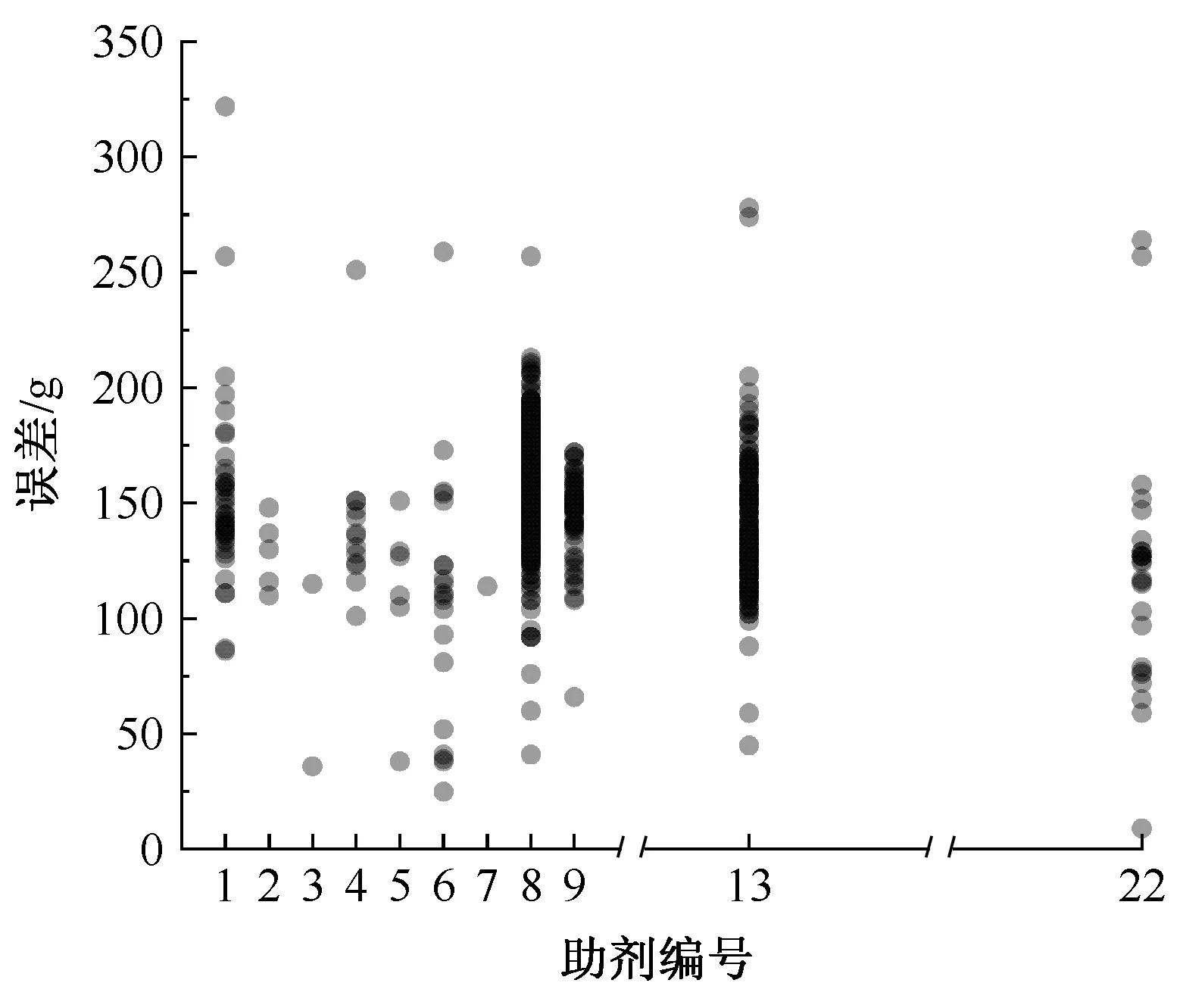
图4 助剂编号与配送误差的关系图Fig.4 Relationship between chemicals ID and distribution error

落料口编号与配送误差的关系如图5所示。可以看出，不同落料口的配送误差的分布中心不同，离散度也不一样，具有较强的规律性，落料编号是影响配送误差的一个重要因素。

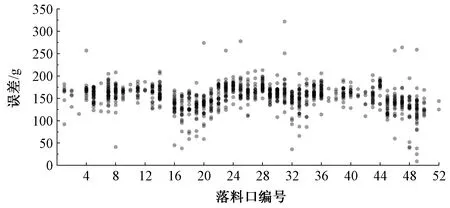
图5 落料口编号与配送误差的关系图Fig.5 Relationship between tank ID and distribution error

配送量与配送误差的关系如图6所示。可以看出，不同配送量在配送时的误差有一定的规律，配送量越多，配送误差越稳定，配送量也是影响配送误差的一个因素。

图6 配送量与配送误差的关系图Fig.6 Relationship between volume and distribution error

根据配送记录的数据分析，配送的条件会影响配送误差，但是因为配送条件较多，配送条件之间相互影响配送精度的数学模型不易建立。神经网络对非线性问题具有较好的解决能力[7]，多层全连接神经网络通过组合低层特征形成抽象的高层标识属性类别[8]，具有较好的回归和拟合能力[9]，加上激活函数给神经元添加非线性因子[10]，可以使用多层全连接神经网络去拟合配送误差模型，计算权重和偏置[11]，得到配送预停值的预测模型，再根据模型计算每1次配送时的预停值，达到减少配送误差的目的。

3 染色机助剂智能配送系统设计

为克服现有技术存在的缺陷与不足，本文提出一种染色机助剂智能配送系统及精度调节方法，从配送的历史记录数据中学习，通过多层全连接神经网络，训练推荐预停值和预计用时的预测模型，得到优化的控制策略。

3.1 控制流程设计

助剂配送系统的控制流程设计如下：

步骤1：上位机智能PC系统通过以太网通信获得企业资源计划(ERP)系统的配送定单数据和染色机中控的配送指令，将配送定单发送给现场PLC控制系统，配送定单里的信息包含助剂编号、染缸号和配送量等。

步骤2：PLC在收到这些数据后，根据助剂编号，打开相应的助剂配送阀，根据染色机料缸号打开相应的落料阀，同时启动变频器，控制转子泵电动机的转动。

步骤3：在助剂配送过程中，转子泵的变频器频率增加，直至达到设定值；当实际配送量接近目标配送量时，变频器频率降低，稳定一小段时间后，PLC将当前变频器的频率、压缩空气气压值发送给上位机智能PC系统。

步骤4：上位机智能PC系统将助剂编号、落料口(落料阀)编号、压缩空气气压值、变频器频率、定单的配送量代入神经网络模型计算得到推荐预停值和预计用时，并将其发给PLC。

步骤5：PLC将本身的设置预停值和推荐预停值按一定的比例计算出最终预停值，在每个扫描周期将定单的配送量减去流量计的计量值，得到剩余配送量；当剩余配送量≤最终预停值时，PLC立刻关闭配送阀，同时关闭落料阀和转子泵电机，由于阀门关闭过程需要几百毫秒的时间，在这几百毫秒内流量计仍然在计量，助剂流到染色机料缸的量约等于最终预停值。

步骤6：PLC将预测用时乘以设定的比例，得到本次助剂配送允许的最长时限，在每个扫描周期将实际用时减去最长时限，当得到的数据≥0时，立即发出声光报警信息，提示人员检查原因和处理故障。

3.2 可变比例控制策略

在助剂配送时，上位机智能PC系统将当前的助剂配送数据代入推荐预停值的神经网络预测模型中计算，得到推荐预停值o1；现场PLC控制系统将基于测试经验值设置的预停值o2，按比例加上推荐预停值o1，计算得到最终预停值o，此可变比例控制策略的计算公式设计为

o=Ko1+(1-K)o20≤K≤1

(4)

在项目实施的初期，K取一个很小的值，可变比例控制策略中起主要作用的是基于经验值设置的控制方式，使系统不会因为网络参数不优的原因导致配送误差大，避免灾难性事件的发生；随着运行收集到的数据量的逐步增多，可对神经网络进行多次训练，网络模型参数越来越接近最优状态，K值逐步提高，上位机智能系统对综合决策的影响就越来越大，当网络训练到最优状态时，K等于1，可变比例控制策略完全由上位机智能PC系统决定。

每次助剂配送时可变比例的K值由预设值决定。采用可变比例控制最终预停值的最大优点是可以对新添加的助剂种类和新增加的染缸实现最快的导入。如果没有可变比例控制策略，每次增加助剂或者增加染缸，原来训练好的神经网络模型不能适用，需要从头开始重新采集大量的配送数据进行网络模型训练，耽误时间。采用可变比例控制策略后，不需要重新训练整个网络模型，可以针对配送中有新助剂或者新落料口的定单的K值取一个较小的值，随着这些新助剂和新落料口的训练次数逐步增多，再相应地增加K值。当观察到推荐预停值连续优于设置预停值时，再将K值取为1。这种可变比例控制策略，在不影响整体控制策略的情况下完成新助剂或者新染缸的导入，可以较好地适应工厂扩产和扩品种的需求。

3.3 全连接神经网络模型设计

预停值和预计用时的全连接神经网络采用多层结构，如图7所示，分为3大部分。第1部分为预停值和预计用时模型共享部分，包括：第1层输入层、第2层隐藏层1，其神经元个数为128，预停值和预计用时共享此层。第2部分为预停值独有模型部分，包括：第3层隐藏层2，神经元个数为256；第4层隐藏层3，神经元个数为128；第5层隐藏层4，神经元个数为64；第6层预停值输出层1。第3部分为预计用时独有模型部分，包括：第7层隐藏层5，神经元个数为256；第8层隐藏层6，神经元个数为128；第9层隐藏层7，神经元个数为64；第10层预计用时输出层2。

图7 预停值和预计用时的全连接神经网络结构Fig.7 Fully connected neural network structure of pre-stop value and predict time

设计的预停值和预计用时全连接神经网络的输入数据均为：定单的目标配送量、助剂编号、落料口编号、压缩空气气压值和变频器频率。

全连接神经网络模型[12]每层的计算公式设计为

(5)

式中：i为本层的第几个神经元；j为对应本层的上一层的第几个输出；m为上一层的神经元个数；n表示第几层神经层；y为输出；x为输入；θ为本层的权重值；b为本层的偏置值；f为本层的激活函数。

每一层的输出作为下一层的输入，即：

xn+1=yn

(6)

模型训练完成后，用于推荐预停值的预测时，最后一层的输出即为推荐预停值，即：

o1=y

(7)

预停值全连接神经网络模型的代价函数公式设计为

(8)

式中：C为代价；L为样本总数；S为样本序号；v1为定单的目标配送量，g；v2为实际配送量，g；z为实际预停值，g。

预计用时全连接神经网络模型的代价函数公式设计为

(9)

式中：t1为助剂配送开始时间，s；t2为助剂配送结束时间，s。

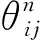
(10)

式中：θ为θij的矩阵；X为xij的矩阵。

4 工程实践

4.1 工程化分析

以上关于智能助剂配送系统的设计是基于理论上的设计，要使其能在实际的工程中落地，需要根据具体的工程进行分析和处理。

每套助剂配送系统中配送阀门数量很多，由于成本的原因，无法在每个配送阀关闭的气路中安装压缩空气气压计，因而在整套系统的总进气处安装了一个公用的压缩空气气压计，由于此气压计在进气组件的减压阀后面，在使用过程中一般将减压后的压强调到0.5 MPa，由于助剂配送时同时打开的阀门数量很少，所以此气压值稳定，在运行时几乎不变，其参与神经网络模型训练的意义不大，因而将压缩空气气压值这个输入项简化去除。

在助剂配送的开始阶段，变频器的频率逐步上升到设定的高速值，当剩余配送量小于设定的值(如2 kg)时，为了控制配送精度，PLC系统将变频器的频率下降至10 Hz，进行低速配送，当剩余配送量小于预停值准备关闭配送阀时，配送泵的频率是固定的10 Hz，因而变频器频率这个输入项也可以简化去除。

通常在一台助剂配送设备中有一套PLC控制系统，一般控制着包含如图1所示的3组系统，由于每组的助剂配送阀、配送泵、流量计和管道不一样，因而它们的配送特性不一样，与预停值和预计用时关连性比较大，因而配送组号也作为全连接神经网络的一个输入项参与训练和预测。

通过如上分析和排除，工程实践时全连接神经网络的输入为4个，分别是组编号、助剂编号、落料口编号、定单配送量。

染厂在使用助剂时，一般是以质量为单位进行计算，但是流量计测量的是体积，输出的是脉冲，在配送时，PLC计量已配送助剂质量的计算公式为

M=Nδρ

(11)

式中：M为已配送助剂的质量，g；N为PLC接收到的流量计的脉冲数；δ为脉冲当量；ρ为助剂的密度，g/mL。

4.2 全连接神经网络模型训练

在深度学习平台TensorFow2.0中搭建上述多层全连接神经网络，输入配送记录数据进行训练，此软件运用梯度反向传递法则计算出每层的θij和bi，这些θij、bi和网络结构组成训练好的网络模型，用于推荐预停值和预计用时的计算。

训练数据是从设计的助剂配送系统在染厂运行40 d得到的实际配送数据，共13 000条配送记录数据，用于本次的训练。训练步骤如下：

步骤1：数据清洗。1)检查是否存在空数据，对空数据进行整条清除；2)查找配送误差异常时的数据，比如配送误差超300 g或者为负值(预停值为0，关闭阀门过程一定会有部分助剂流过阀门)，超300 g的情况一般为阀门内有异物，没有完全关闭，为硬件问题，需要剔除此条数据；负值为流量计异常，也需要剔除。3)查找配送用时异常的数据，比如配送量除以时间超过平均值50%的数据，一般是在配送时出现硬件问题或者人工按了暂停键所导致配送用时特别长，此类数据需要整条剔除。

步骤2：将数据集切割成2个数据集，其中80%为训练数据集，20%为校验数据集。

步骤3：对训练数据集求平均值和样本标准差，计算公式如下：

(12)

(13)

步骤4：将训练数据集和校验数据集进行数据标准化，标准化公式如下：

(14)

(15)

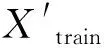
步骤5：设置训练参数，批的大小设定为1 024，7个隐藏层的激活函数均使用Relu函数，用Adam算法作为梯度下降的损失函数优化器。根据校验集的损失值改善情况降低学习率，每经过5个轮次(epochs)训练，若模型效果不再提升，就缩小学习率进行训练，其中设置值为：学习率调整倍数为0.8，最小学习率为0.000 000 01，轮次为200。

步骤6：对模型进行训练，在每个epoch输出训练数据和校验数据的损失值(Loss)和平均绝对误差(MAE)，得到第200次epoch训练结果，如表1所示。

表1 模型训练结果对比表Tab.1 Comparison of model training results

采用图型化表示训练过程的Loss值和MAE值随训练轮数变化的曲线，预停值的Loss值和MAE值的训练结果曲线如图8所示，预计用时的Loss值和MAE值训练结果曲线如图9所示，均能够快速收敛到一个较小的值，说明模型起到了较好的拟合效果。

图8 预停值与训练轮数曲线图Fig.8 Curves of pre-stop value and training epochs. (a) Loss curves of pre-stop value；(b) MAE curves of pre-stop value

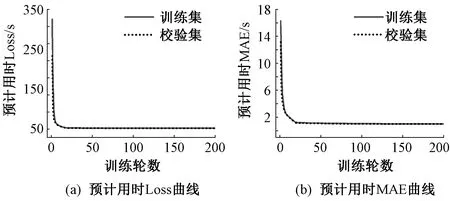
图9 预计用时与训练轮数曲线图Fig.9 Curves of predict time and training epochs. (a) Loss curves of predict time value；(b) MAE curves of predict time value

4.3 神经网络模型应用

在助剂配送系统的PC机上安装Python和Tensorflow2.0，运行预测网络模型，通过csv文件来实现配送数据的输入和神经网络模型预测数据的输出。助剂配送系统的上位机软件用C#语言编写，它将需要预测的数据写入到csv文件中，从模型预测输出的csv文件中读取预测结果数据。

步骤1：在助剂配送定单启动时，PLC启动配送过程计时器，上位机软件将配送数据写入到csv格式的输入数据中。

步骤3：预测程序将标准化的数据代入预测模型中进行计算，得到推荐预停值和预计用时，将这2个值写入到模型预测输出的csv文件中。

步骤4：上位机软件从模型输出的csv文件中读取推荐预停值和预计用时，通过OPC通信方式将这2个值写入到PLC系统的指定寄存器里。

步骤5：PLC系统计算最终预停值，使用最终预停值与剩余配送量的对比关系决定配送停止时机；PLC系统将预计用时乘以150%作为配送过程的最大时间限制值，若配送时间超出此值，PLC系统停止配送，发出声光报警，并在现场HMI上面显示报警信息，提示人员检查故障原因。

为了使预测系统不会因为意外原因出错导致助剂智能配送系统停机，使用try语句对可能出现报错停止的地方进行恢复处理，确保系统的稳定运行。

4.4 工程实践结果

使用4种预停值模式在染色机助剂配送系统上各执行1 000次配送任务，其中各模式预停值设置的区别如下。

模式1：预停值设置为0。

模式2：对7个配送支路分别进行配送测试，使用测试经验值设置各个配送支路的预停值。

模式3：使用13 000条配送记录进行第1次神经网络模型训练，使用第1次训练得到的全连接神经网络模型计算每次助剂配送的推荐预停值o1；采用可变比例控制策略的计算方式，按K=0.5将基于测试经验值设置的预停值o2，按比例加上推荐预停值o1，计算得到最终预停值o。

模式4：使用18 000条配送记录进行第2次神经网络训练，使用第2次训练得到的全连接神经网络模型计算每一次助剂配送的推荐预停值o1；按K=1计算o，此时o等于o1，最终预停值完全由神经网络的输出决定。

此4种模式下配送助剂得到的助剂配送误差与配送次数的分布图如图10所示。

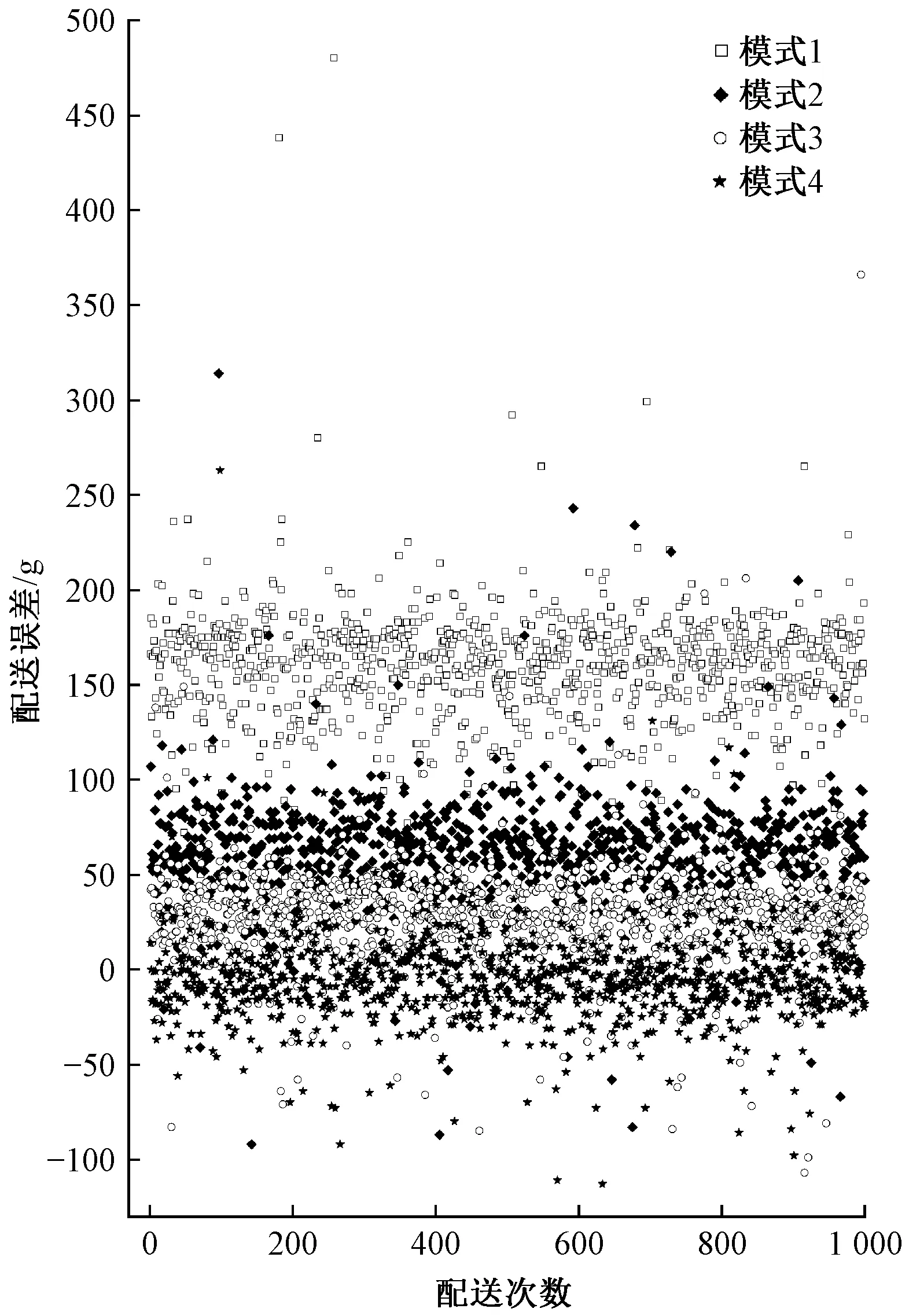
图10 模式1～模式4助剂配送误差对比图Fig.10 Graph of distribution error and distribution times of mode1 to mode 4

从图10可以看出：在没有设置预停值时，配送误差最大，离散度也最大；采用测试经验值模式时配送误差下降了一些，离散度略有下降；采用神经网络和测试经验值综合决策模式时配送误差再次下降，离散度也再次下降；完全采用神经网络预测预停值的结果是最优的，配送误差最小，离散度也最小。

表2示出4种模式各配送1 000次的配送误差结果对比。可以看到配送误差的方差、标准差和平均绝对误差均从模式1～模式4逐步降低，模式4的标准差为23.8 g，平均绝对误差为16.1 g；模式2的标准差为30.1 g，平均绝对误差为61.4 g。可见，模式4取得了较好的控制效果。

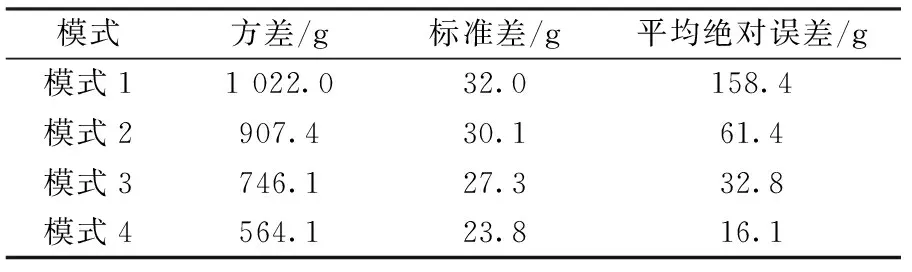
表2 4种模式配送误差结果对比Tab.2 Comparison of distribution error results of four modes

模式4配送方式执行1 000次配送的配送实际用时、预计用时与配送次数的关系如图11所示，除其中有1次配送实际用时特别长外，其余999次实际用时都在120 s以内，且与预计用时都比较接近。

图11 配送实际用时、预计用时与配送次数图Fig.11 Graph of actual time, predict time and distribution times

使用模式4配送方式执行1 000次配送，配送实际用时与预计用时之间的误差数据统计如表3所示，包含第253次配送时的硬件异常引起的超时(用时758 s)，标准差为23.5 s，平均绝对误差为1.8 s；若将第253次的异常配送记录剔除，对余下的999次配送记录做统计，则得到的标准差为1.6 s，平均绝对误差为1.0 s，标准差和平均绝对误差都比较小，说明助剂配送的预计用时接近实际用时，预计用时模型起到了较好的预测效果。

表3 配送实际用时与预计用时的误差结果对比Tab.3 Error statistics between actual and predict distribution time

在模式4实验时，启用了根据预计用时监控实际配送过程是否超时的功能，设置成当实际配送用时超过预计用时的150%时，系统发出报警。在第253次配送时，由于硬件异常导致阀门没有打开，无法配送助剂，当系统检测到配送用时超过预计用时的150%时，立即发出声光报警，提醒人员检查设备故障。采用神经网络计算配送预计用时，可以较快发现设备故障，提高设备的利用率。

5 结 论

本文所设计的染色机助剂智能配送系统，使用全连接神经网络模型预测助剂配送的预停值，比基于测试经验得到的预停值更准确，能得到比较好的配送精度，达到减少助剂用量和提高产品质量稳定性的技术效果；使用全连接神经网络模型预测助剂配送所需的时间长度，进行配送过程动态监测，解决了助剂配送过程时间跨度过大难以监控的技术问题，实现对每个定单的助剂配送过程执行超时监测和报警的功能。此新型助剂智能配送系统达到了节约助剂、减少排放、保护环境、提高配送精度的效果，具有一定的社会价值和经济价值。本文研究对于采用类似配送工艺的盐碱配送系统或母液配送系统也具有一定的参考价值。