基于数据挖掘的电能误差数据自动化校正方法
杨军,庄文德,张育辉
(南方电网数字电网研究院有限公司,广东广州 510520)
在实际分析电能数据时,受到外部环境的影响,常常会产生误差[1-2],为此,研究误差数据的校正成为了当前相关领域的研究重点。对于规模较大的电网网络,其误差数据规模也更为庞大[3],对实际的校正工作产生了较大的阻碍[4-6],为此,设计一种误差数据自动化校正方法是很有必要的。
文献[7]提出基于TDR 的自动墒情站监测数据校正,引用了正确的电能数据估计值替换原有的误差数值,但该估计值的精度不高,导致最终的校正正确率较小。文献[8]提出基于线电压差积分的电能误差检测及校正方法,整合了误差数据的特征,定义了误差数据的校正状态,但状态数据产生了一定的噪声,导致实际校正时的正确率变小。
综合当前研究成果来看,建立自动化校正方法很有必要,为此,提出基于数据挖掘的电能误差数据自动化校正方法。
1 数据自动化校正方法
1.1 挖掘供电网误差电能数据
在挖掘供电网误差电能数据时,划定相同区域的供电网作为处理对象[9],整理为不同类别的数据集后,采用主成分方法处理采集得到的电能数据,处理过程可表示为:
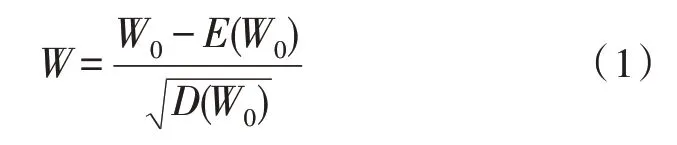
其中,W0表示采集得到的电能数据,E(W0) 表示计量得到的电能数据,D(W0)表示标准化电能数据。划分上述电能数据为不同的时间间隔等级,划分过程可表示为:

其中,j表示配电网的节点,n表示配电网节点电能表的数据,Wj表示时间间隔周期内的电能数据。假设实际间隔内的时间周期呈独立分布[10],此时挖掘得到的电能数据呈现正态分布,电能数据状态可表示为:

其中,e(j)表示电能数据间的线性关系,η2表示电能数据误差方差,I表示电能数据的单位矩阵,其余参数含义不变。不断增大采集电网的范围后[11],在上述电能数据状态的控制下,区域内的电能数据的变化如图1 所示。

图1 采集电能数据的变化
由图1可知,不同采集周期下,受到外部环境的干扰,电能数据中产生了部分的误差数据,对该部分误差数据进行处理[12],确定电能数据中的误差数据指标。
1.2 确定误差数据指标
在上述确定得到的电能误差数据下,同区域同周期不同分支内的电能数据,受到外部随机噪声的影响,导致电能数据误差,可表示为:
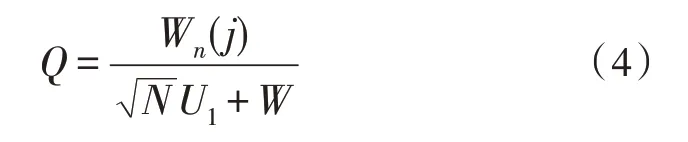
其中,Q表示电能误差数据集合,N表示实际产生噪声数据的支路数量,U1表示电能数据的协方差特征值。在该数据控制下,将电能数据误差指标数量作为一种误差数据指标。因外部供电电压较低而导致电能数据产生偏差[13],该部分的电能数据误差就可表示为:

其中,M表示实际配电网的供电量。Wz表示电网支路中与预期的数值差缺少的电压数值,y为预期电压数值,在统计区间内,配电网用户在限值范围内产生一定的累积[14],此时实际运行的电压与预算电压产生的误差,该部分误差就可表示为:

其中,Ri表示配电过程产生的电能误差,ti为配电网用户在限值范围内的电压差值,q为配电网用户极限电压值,M表示电能数据实际运行产生的电能,T表示采集电能数据周期。在上述统计周期内,供电网内的电压会产生一定的暂降,进而在供电网中产生一定的电能误差,可表示为:

其中,Hi表示电能数据的暂态误差,ΔDi表示配电网的统计时间周期,其余参数含义不变。汇总上述得到的电能误差数据,构建误差自动校正方法。
1.3 实现对电能误差数据的自动化校正
将不同误差来源的数据划分为不同的数据组,将数据组中的数据划分为已测数据与未测数据,并构建一个状态判断公式,可表示为:

其中,P表示全部的误差数据,P1表示已测数据,P2表示未测数据,A表示非零列的电能误差数据。定义上述电能数据为一个无显著状态,协调两个状态的稳态后,形成一个电能稳态数据,可表示为:

其中,f(x)表示电能稳态约束函数向量,B表示未测显著参数,n表示电能稳态参数。在上述电能稳态数据的控制下,构建得到的校正模型就可表示为:

其中,s表示电能误差数据的数量,ai表示配电网节点函数,F表示实际产生的电能误差数值,C表示非容性节点相关系数,其余参数含义不变。在上述校正矩阵的控制下,设定校正矩阵的校正周期[15-16],使用该校正周期参数不断控制电能误差数据的采集过程,最终实现对电能误差数据的自动化校正。
2 仿真实验
2.1 实验准备
选定一供电网网络拓扑结构作为电能数据的采集对象,使用的电网网络拓扑结构如图2 所示。
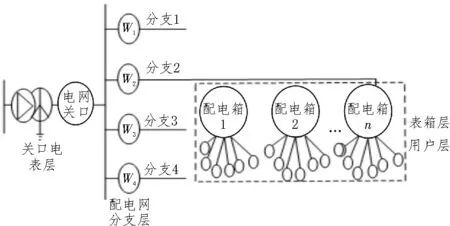
图2 选定的供电网络拓扑结构
在图2 所示的供电网拓扑结构中,供电线路采用放射式的接线形式,控制供电网中的母线电压为10 kV,并连接分支馈线,并在二级配电设备的控制下,通过分支箱的接线形式,实现电能的分支输送。采集供电网络拓扑结构中的电能数据,采集得到的电能数据如表1 所示[17]。
使用表1 采集得到的电能数据,以文献[7]方法、文献[8]方法及该文校正方法进行实验,对比三种校正方法的性能。
2.2 结果及分析
基于上述实验准备,控制三种校正方法处理表1中的电能数据,定义三种校正方法累积的校正误差可计算为:

表1 采集得到的电能数据

其中,Xi表示采集得到的电能数据集,表示显著误差数据,Q表示误差显著参数。在上述计算公式控制下,三种校正方法校正时产生的误差,结果如表2 所示。
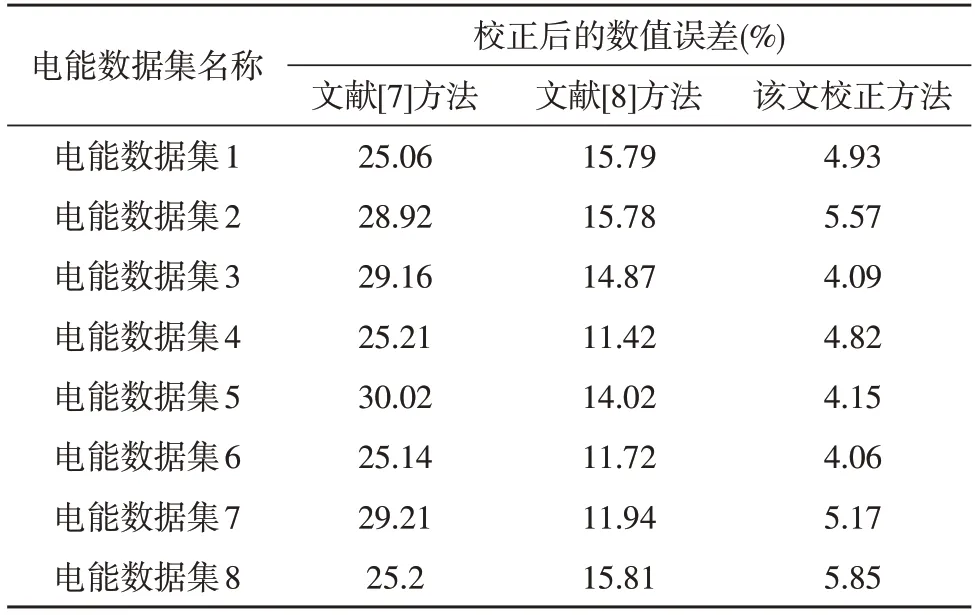
表2 三种校正方法产生的误差
由表2 所示的校正结果可知,控制三种校正方法处理相同的误差数据集,根据计算得到的校正误差可知,文献[7]方法校正误差在27%左右,实际校正效果较差,文献[8]方法产生的校正误差在12%左右,校正误差较小,且实际校正效果较强。而设计得到的校正方法产生的校正误差在4%左右,与两种对比校正方法相比,设计得到的校正误差最小,实际校正误差数据的效果较强。
当电能数据产生数值变化时,则定义为一次异常数据替换过程,统计三种校正方法可替换异常数据的数量,结果如表3 所示。
根据表3 所示的数值结果可知,控制三种误差数据校正方法替换原有的电能误差数据,文献[7]方法可替换的误差数据数量在21-29 组之间,可替换的误差数据数量较少,文献[8]方法可替换的误差数据数量在32-38 组之间,而设计得到的校正方法可替换误差数据组的数量在40-44组之间,与两种常规校正方法相比,该种校正方法几乎可替换所有的误差数据。
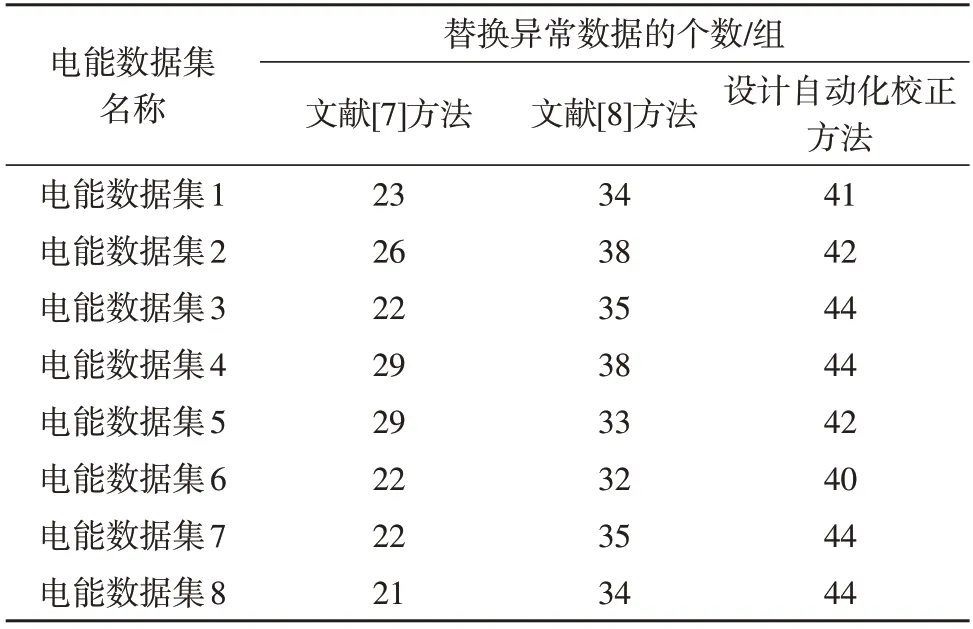
表3 三种校正方法替换异常数据个数结果
保持上述实验环境不变,在使用三种校正方法处理误差数据时,控制误差数据集迭代100次,统计三种校正方法正确校正的数量,计算得到校正正确率,结果如图3 所示。

图3 三种校正方法校正正确率结果
由图3 所示的校正正确率结果可知,控制数据集中的数据迭代100 次后,变换电能误差数据的形式,根据统计文献[7]方法平均正确率数值在85%左右,得到的正确率数值较小,文献[8]方法的平均校正方法平均正确率数值在94%左右,实际校正正确率数值较大,而设计校正方法平均正确率数值在97%左右,与两种常规校正方法相比,该种校正方法校正正确率最高,实际的校正效果最佳。
3 结束语
配电网结构越来越复杂,导致电能误差数据量的增加,为此提出基于数据挖掘的电能误差数据自动化校正方法,实验结果表明所设计方法能够改善原有校正方法存在的不足,为今后研究误差校正提供一定的理论支持。

