LDPC 码与数字图像加密
邵一丹,王中训,李心宇,张梦雨
(烟台大学物理与电子信息学院,山东烟台 264005)
在当今世界,网络信息技术几乎覆盖到了每一个角落,生活中的很多方面都离不开计算机。人们享受着计算机带来巨大便利的同时,隐私信息也面临着被泄露的风险。
图像包含的信息量较多,作为信息存储和传输过程中的一种重要载体,被广泛应用[1]。图像在人们的生活中发挥着越来越重要的作用,大量的图片在社交网络中传输,但也容易泄露个人的隐私。比如,有的人用他人的照片通过人脸识别取走当事人的快递,在网络世界中,人们也可以通过图像来获得各种各样的信息,如何保证图像信息的安全传输和存储,成为信息安全的一个及其重要的领域[2]。
为了提高数字图像安全性,这里运用了2D Logistic-Sine 混沌系统与LDPC 码相结合的图像加密方案,相比较一维的混沌系统,有着更为优良的特性,不易被破解,从而提高了密图的安全性。最后通过Matlab 进行仿真分析,得到了不错的加密效果。
1 LDPC码
1.1 LDPC码概述
LDPC(Low Density Parity Check)码概念首次出现是在1960年,由Gallager 教授在其博士论文中提出。由于相较于校验矩阵H的长度,它的行列中存在着特别小的非零数[3],即“1”的数目要远远比“0”的数目小得多。这也是LDPC 码之所以会被称作为低密度奇偶校验码的原因。正是出于这个原因,使得LDPC 码的复杂程度低,并且提高了其性能,使得LDPC 码得到了较为广泛的应用。
H为校验矩阵,其大小设定为m×n,并用它来对LDPC 码进行定义。在校验矩阵H当中,校验信息由每行来对应,码字信息则由列与其对应。校验矩阵H中每列非零元素的个数称为列重[4],并用λ来表示;同理可得,行重则是每行非零元素的数目,这里用ρ来表示。

校验矩阵H有着如下几个特点:
1)每行的元素1数目是一致的。“1”的数目即为行重。在如式(1)所表示的校验矩阵H中,该行重为3。
2)每列的元素1 数目是相同的。“1”的数目即为列重。在如式(1)所表示的校验矩阵H中,该列重为2。
3)任何两行或者两列之间,非零元素重合的次数小于或等于1。不是零的元素分布较为稀疏。
当HcT满足等于零的条件时,也可以用方程的方式来表述LDPC码,校验方程如式(2)所示:

除了校验矩阵和方程这两种方式能表述LDPC码之外,Tanner 图也可用于表示LDPC 码。Tanner 图中运用图形来表示,更加清楚地展示了码元节点跟校验节点之间的关系。利用码字的校验方程来表现码字就是Tanner 图的本质所在。
两种顶点(比特节点以及校验节点)出现在Tanner图当中。从某一个节点,例如从C0开始,不经历重复的边,最终又返回到这个节点的闭合回路称为环。在闭合回路中走过的边的数目是环长,最短环长也可以称作围场,指的是经历边数最少的环。Tanner 图如图1 所示。

图1 H(6,2,3)校验矩阵的Tanner图
在Tanner 图里存在着循环,在译码的过程中有概率会出现校验信息重复反馈的情况,从而使得译码的准确率降低,因此,构造校验矩阵的过程中应尽量避免围长较短的循环产生[5]。
1.2 BP译码方式
经典的置信传播(Belief Propagation,BP)算法,是一种软判决算法[6]。BP 译码算法的原理:其译码思想和BF 类似,在信息传输过程中沿着Tanner 图边进行传递,这种传递是双向的[7]。
BP 译码方式第一步就是将变量节点进行初始化,然后每个变量节点通过与校验节点相连的边将概率信息传递给校验节点[8]。信息经过校验节点计算更新之后再传回到变量节点中,接着,变量节点依据更新以后的信息做判决,这便是一次迭代的过程。最终结束译码的条件是找到了允许使用的码字或者是到达了最大的迭代次数。通过多次迭代计算使得译码结果更加精准,误码率更低[9]。
若xl表示变量节点,sm代表的是校验节点,那么表示的是xl向sm传递的信息,则sm传递给xl的信息就用来表示。不包含xl这个变量节点的L(m)集合记为L(m)l,不包括sm这个校验节点的M(l)集合记为M(l)m。
如果Hml满足等于1的条件,则l执行下面的步骤。
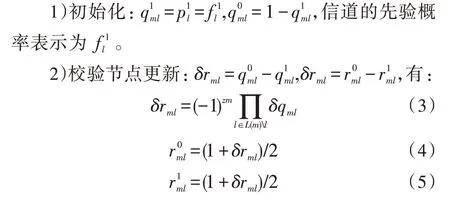
3)变量节点更新如下:

在上述公式中,aml是一个比较特殊的存在,它可以使得与两者的和保持为1。
4)似后验概率更新如下:

其中,al与aml作用相类似,它的存在可以使得与两者的和保持为1。
5)比特判决,当的取值大于0.5时,xl的数值就等于0;否则,判定的xl数值就等于1,l=1,2,…,N。当HTx=0 或者到达了最大迭代次数时,结束译码,输出译码结果x,如果还未满足要求,则跳回到步骤2)循环执行。
2 混沌系统
混沌系统有许多特性,如初值敏感性、随机性、遍历性和不可预测性等特点,被广泛应用于图像加密[10]。
2.1 Logistic
Logistic 映射表现为一种迭代或映像过程[11]。Logistic 映射用数学公式可以描述为[12]:

经过多次的实验,如果想要映射处于混沌的状态,μ要满足的条件是3.569 945<μ≤4。参数μ与数值4 越相近,x的取值范围越是平均分布在0 和1 的整个区域[13]。其结果展现出了伪随机分布状态。μ=4时,Logistic 映射进入满映射状态[14]。
2.2 Sine
Sine 映射公式为:

2.3 2D Logistic-Sine
2D Logistic-Sine 公式为:

其中,α∈[0,1]。
2D Logistic-Sine 的加密流程如图2 所示。

图2 加密流程
3 加密方案
首先,把待加密处理的图像进行位平面的分割,得到了8 个二值位平面,再对最高的两位位平面进行LDPC 编码,重构位平面,得到10 bit 灰度图。设定初值x0=0.5,y0=0.8,a=0.99。利用混沌系统对图像进行置换以及行列扩散操作。
原始图像如图3 所示。

图3 原始图像
首先,将图像进行置乱操作,结果如图4 所示。

图4 置乱后图像
对图像再进行行扩散与列扩散操作,结果分别为图5 与图6 所示。

图5 行扩散后图像

图6 列扩散后图像
分离出高两位位平面作为内部密钥输出,剩余8位位平面构成的密文图像输出。
最终加密图像如图7 所示。

图7 最终加密图像
解密就是取反的过程,依次进行列解密、行解密、置乱恢复。分离出高四位位平面,经过LDPC 译码最终得到解码之后的位平面。将解码之后的位平面与6个位平面重构,得到解密图像如图8所示。

图8 解密图像
4 Matlab仿真实验及分析
4.1 直方图分析
直方图是基本统计特征,它所表示的是灰度级函数。分布越均匀,越能掩藏明文图像像素值的散布情况,使对抗人员难以破解,获得相关的信息[15]。
直方图的定义如下:

原图像的直方图如图9 所示,加密后直方图如图10 所示。

图9 原图像直方图

图10 加密图像直方图
加密后的直方图较为均匀,说明加密效果较好。
4.2 相邻像素的相关性
图像相邻像素相关性能够真实反映图像相邻位置像素灰度值的相关程度[16]。
计算公式如下:

表1 为图像的相关性。

表1 图像的相关性
相邻像素点的相关性取值越小,表明了图像相邻像素灰度值关联程度就越低,图像就更加的无序混乱,所以应使加密后的图像相邻像素的相关性系数越小越好。
4.3 信息熵
信息熵反映了灰度值的分布状态。如果灰度值均匀分布,就有着更大的信息熵。
原始图像信息熵为7.009 7;加密图像信息熵为7.997 2,接近于8。越接近于8,经过信息熵来获取图像的信息就越困难。
4.4 密钥敏感性
选择不正确的初值进行解密,如x0=0.499 99,y0=0.800 01,再进行解密,错误解密图如图11 所示。

图11 错误解密图
解不出原始图像,说明该系统较为敏感。
4.5 密钥空间大小
假设精度为10-16,那么该算法的密钥空间为1048,密钥空间大于Logistic 映射的1030,更能抵御穷举攻击。
5 结论
该文采用LDPC 码与2D Logistic-Sine 相结合的加密方法,对图像进行加密,加密后无法用肉眼获得有用信息,加密效果较为理想。而且相对于一维的混沌系统,有着更大的密钥空间,也相对不容易被破解,提高了安全性,然而LDPC码的编译码速率还有待进一步提升。

