针对ATSC 3.0标准傅里叶信道估计算法的改进

尚玉龙，田建杰

（江苏理工学院 电气信息工程学院，江苏 常州 213001）

1 概 述

现今最新的数字地面电视标准是ATSC 3.0。ATSC 3.0标准采用了分层复用技术（Layered Division Multiplexing，LDM）。LDM具有两层，分别是核心层（Core Layer，CL）和加强层（Enhanced Layer，EL）。CL的覆盖范围大，主要提供一般电视服务，而EL覆盖范围小，主要提供高级别电视服务[1]。因此，需要采用单频网（Single Frequency Network，SFN）来解决全域覆盖问题，例如分布式多线方案，把传送天线设置在覆盖域中的不同位置，传送相同的服务信号[2]。

在SFN场景下，增大的信道延迟扩展对信道估计提出了很大的挑战。ATSC 3.0标准一般在多频网场景中采用线性插值信道估计，而在SFN场景下，建议采用离散傅里叶变换（Discrete Fourier Transform，DFT）信道估计以应对更大的信道延迟扩展。然而，由于DFT信道估计算法要求导频信号数量必须是2n（n是正整数），因此DFT估计算法在一部分ATSC 3.0中的导频插入方案下难以正常工作。

因此，本文建议了一种一般化DFT信道估计算法，其可以在任意导频插入方案下正常工作。同时，建议的算法在计算复杂度上比传统DFT算法更低。仿真结果表明，当导频数量是2n时，建议算法与传统DFT算法保持一致；当导频数量不是2n时，建议算法依然正常工作，CL和EL均可正常工作。此外，本文推导了建议算法的理论均方误差，其与仿真结果保持一致，从而与仿真进行了相互印证。

2 系统模型和传统DFT信道估计

ATSC 3.0的物理层系统框图如图1所示。CL和EL具备独立比特交织编码调制链路（BICM）。CL一般工作在低信噪比（Signalto Noise Ratio，SNR）区间以提供鲁棒性强的一般化服务，而EL一般工作在高SNR区间，以提供更高级别的服务[3]。ATSC 3.0定义CL和EL的能量比为注入水平（Injection Level，IL），通过IL的变化来平衡不同场景下的CL和EL服务质量。在接收端，快速傅里叶变换（Fast Fourier Transform，FFT）的输出可以表示为

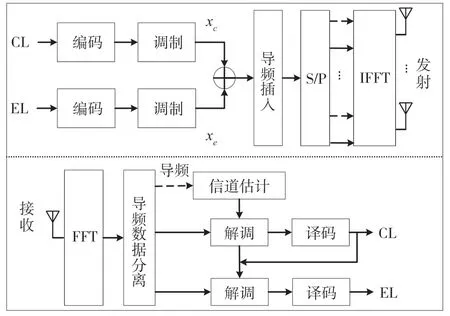
图1 ATSC 3.0物理层系统框图

y=Xh+n=XFg+n（1）式中：h和g分别是信道频域响应（Channel Frequency Response，CFR）和信道冲激响应（Channel Impulse Response，CIR），F和n分别是N×N傅里叶矩阵和N×1高斯噪声向量，ni~N(0,σn2)，X是N×N的对角矩阵，其对角元素由数据符号和导频符号组成。

接收端先进行信道估计，而后把EL信号当作噪声对CL信号进行解调译码，消除CL信号干扰后再对EL进行解调译码。

传统DFT的信道估计算法的系统框图如图2所示[4]。

图2 传统DFT信道估计框图

假设导频间隔为q，那么导频数量为P=N/q，因此必须满足q=2n才能保证P为整数，传统DFT算法才能正常工作。第i个导频信道可表示为

根据最小二乘估计可得

通过傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）得到CIR。需要注意的是，CIR的长度一般很小，小于正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）的保护间隔（Guard Interval，GI）。由于接收端并不知道CIR的具体长度，因此通常将GI的长度G当作CIR的长度。因此，CIR可表示为

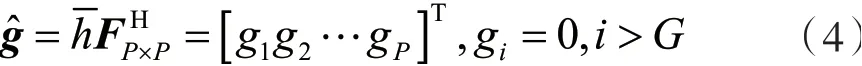
式中：(·)H指矩阵的复共轭运算。最后在CIR后补0，再通过N-FFT得到CFR。这里需要注意的是，根据经典估计理论，样本数量需要大于被估计参数的数量，因此P≥G[5]。

3 改进的DFT信道估计算法

DFT估计算法的核心思想是估计更短的CIR而后通过FFT转换为CFR。根据式（1），导频信号向量可转换为

这里yP=[y1yq+1…y(P-1)q+1]T，FP×N是根据导频位置从傅里叶矩阵中抽取其中的P行组成的矩阵。假设CIRg的长度被认为是L（一般认为L=G），因此，式（5）可以继续转换为

这 里FP×L是FP×N的 前L列 组 成 的 向 量，gL=[g1g2…gL]T。根据LS准则，需要最小化损失函数，可表示为

对其求导并令其等于0，可得LS估计如下：

根据式（6）和式（8），该算法的均方误差（Mean Square Error，MSE）可表示为

式中：σP是导频信号的幅度，η是一个常数，的迹，由于导频符号及其位置在接收端已知，因此式（8）可以化简为

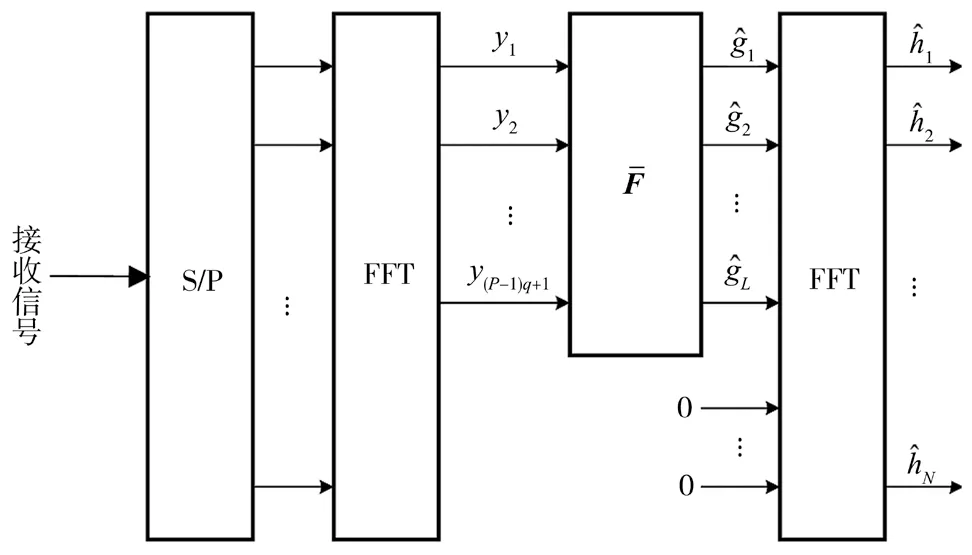
图3 改进的DFT信道估计框图

对于复杂度比较，一般使用复乘法的次数来衡量。不考虑两种算法相同部分，根据式（3）和式（4），传统傅里叶估计算法的复杂度为P+P2；由式（12）可得改进的DFT估计算法的复杂度为PL。对比可知，本文建议的算法比传统算法的复杂度稍低。

4 仿真结果及分析

本节通过MSE和比特误码率来对比传统DFT算法和改进的DFT算法。仿真场景是2个发射机的SFN场景，最大延迟扩展为90% GI的长度，信道模型为准静态莱斯，其他参数如表1所示。

表1 仿真参数

线性插值（Linear Interpolation，LI）、传统DFT以及改进的DFT算法的MSE仿真结果如图4所示。当q=8时，本文算法与传统DFT具备相同的性能，均优于LI算法。但是当q=6时，由于P=2n，传统DFT算法不工作，性能低于LI算法，本文算法依然可以正常工作。此外，本文算法的仿真MSE与理论MSE在两种情况下均保持一致。

图4 不同导频间隔下的MSE性能对比

图5给出了ATSC 3.0的CL和EL在不同信道估计算法下的比特误码率（Bit Error Ratio，BER）曲线。如图5所示，采用传统DFT和LI时，CL和EL均无法正常工作，因为CL和EL的LDPC码的工作区间分别为BER＜0.3和BER＜0.1[3]。而采用本文算法时，CL和EL的BER均正常，随着SNR的增加而下降，完全覆盖LDPC码的工作区间。与完美信道情况相比，CL和EL性能均有2 dB的损失。

图5 导频间隔q=6时不同算法的BER性能对比

5 结 语

本文针对ATSC 3.0标准提出了一种改进的DFT信道估计算法。不同于传统DFT，本文算法解除了导频间隔对传统DFT算法的限制，具备更多的设计自由度。仿真结果表明，在SFN场景下，本文算法在导频间隔不是2的幂次数时，性能远远优于传统DFT和LI算法；在导频间隔是2的幂次数时，性能与传统DFT算法性能保持一致。此外，在计算复杂度方面，本文算法略优于传统DFT算法。