基于时变矩GEV频率分布模型的设计暴雨推求

龙 群 黄亚珏

（水利部珠江水利委员会水文局，广东 广州 510611）

0 前言

设计洪水的分析计算是防洪工程设计、建设的基本依据，设计暴雨常常作为设计洪水计算模型的输入条件。随着气候变化加剧和大规模人类活动影响，暴雨序列呈现出不同程度的非一致性特性，违背了传统GEV、P-Ⅲ等频率分布模型使用时基于一致性的基本假设，基于常规频率分布模型分析设计暴雨进而计算得到设计洪水的结果可靠性有待考究。同样地受气候环境变化、下垫面条件变化影响，洪水序列呈现出了更为显著的非一致性［1-2］。国内外学者就水文资料的非一致性做了很多有益的探索及研究，目前关于非一致性水文频率分析方法的代表性研究成果主要分为两类［3-7］：一是基于还原/还现途径构造一致性序列的方法；二是基于非平稳系列的直接频率分析计算方法。在基于还原/还现途径的方法中，可参考暴雨资料修正洪水资料的非一致性问题［8］，但当暴雨资料的一致性也不能满足时，则可采用基于非平稳系列的直接频率计算方法。直接频率计算方法大致可以分为两类：针对序列个体并非来自同一总体时，构建基于混合分布或条件概率的非一致性频率分析方法；当样本个体存在一定的趋势性或难以明确的非一致性时，可以采用基于时变矩的频率分析方法。这些方法在水文资料直接计算设计洪水时常被用来讨论，但在设计暴雨推求设计洪水中却鲜有见到［9-11］。本研究以最大三日暴雨为例，采用时变矩的GEV频率分布模型，与基于一致性假设的常规模型所得设计暴雨成果进行对比，分析各个模型在暴雨资料推求设计洪水中应用的可靠性。

1 时变矩GEV频率分布模型

1.1 构建时变矩频率分布模型

在平稳广义极值分布模型GEV 中引入时间变量t 构建非平稳广义极值分布模型GEVt，所述非平稳广义极值分布模型GEVt的表达为式（1）。

式中，κt为形状参数，μt为位置参数，αt尺度参数，x为历年最大三日雨量，t为时间。

根据形状参数κ、位置参数μ、尺度参数α 分别与时间变量的关系，构建的非平稳广义极值分布模型 GEVt有 多 种 表 现 形 式 ，如 ：GEV1(μt= μ1+μ2Yt,α ,κ )、GEV2(μt= μ1+ μ2Yt+ μ3Yt2,α ,κ ) 或者 GEV11(μt= μ1+ μ2Yt,αt= exp(α1+ α2Yt),κ )，其中的Yt为年份统计变量。

1.2 极大似然法（ML）求解模型参数

构造极大似然函数［12］为式（2）。

式中：n为样本容量；其中κt≠ 0。对式（2）取对数得到式（3）至式（7）。

1.3 优选非一致性频率分布模型

采用AIC 准则对上述模型进行优选，表达式为式（8）。

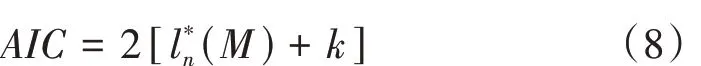
式中：k 为模型参数个数；l*n(M) 为模型 M 的极大似然指数。AIC 值越小，说明模型的适用性和复杂性越好，侧面反映所求模型参数的可靠性。

2 研究实例

本研究以某雨量站1959—2016 年年最大三日暴雨量资料为例，采用Mann-Kendall检验法对系列的趋势性、变异性进行检验；在明确存在非一致性时，采用多个时变矩的GEV 模型进行统计分析；通过AIC 准则优选统计模型，与常规GEV 模型求得的设计暴雨、超越概率进行对比分析［12］。

2.1 系列非一致性诊断

利用该站58 年的年最大三日暴雨量资料绘制的时间序列图见图1，可以得出年最大三日雨量有较为明显的下降性趋势。采用Mann-Kendall 检验法对其趋势性作进一步检验，在5%的显著性水平下，Mann-Kendall 法检验结果表明，系列不仅具有明显的下降性趋势，还存在多个突变点的跳跃性变异，如图2所示。

图1 年最大三日暴雨量时间序列图

2.2 基于时变矩的GEV模型分布参数求解

通过常规GEV频率分布模型，为方便计算，令κt为常数，构建 GEV1、GEV2、GEV11，采用极大似然估计（ML）方法进行分布参数的求解，具体结果如表1所示。

2.3 基于时变矩的GEV模型比较

通过上节得到的分布参数，求解各模型P=2%与P=1%的设计暴雨量，如图3、图4所示。可见，常规的GEV 频率分布模型所得到的设计暴雨量为一常数，而 GEV1、GEV2、GEV11所得的设计暴雨量随年份呈现递减的趋势。其中GEV1所得结果相对稳定，随年份变化不明显，在图中与常规的GEV 模型所得结果几乎重合；GEV11所得的设计暴雨量随年份变化下降最为明显，且在统计的前期设计暴雨量明显大于其他模型的所得结果，在统计的后期所得结果又明显小于其他模型；GEV2所得的设计暴雨量从统计开始便一直低于常规GEV模型的所得结果，并一直随着年份减小。

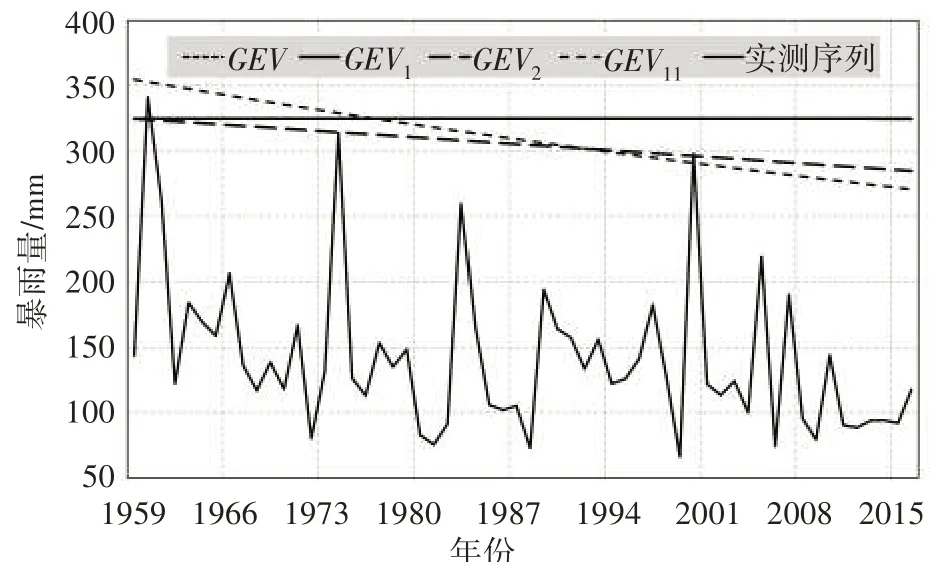
图3 各模型P=2%的设计暴雨量

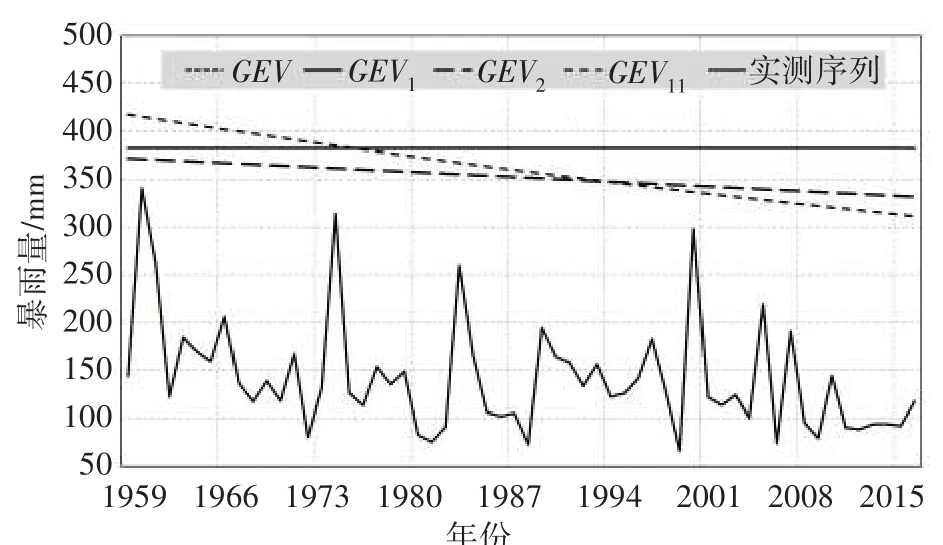
图4 各模型P=1%的设计暴雨量

根据AIC 准则，AIC 值越小，说明模型的适用性和复杂性越好，侧面反映所求模型参数的可靠性。通过表1 所得到的AIC 值进行对比分析，不难发现GEV2的AIC 值最小，其适用性较其他模型好，也优于常规的GEV模型。

表1 基于ML方法得到的非平稳GEV分布的参数估计成果

表2 列出了GEV、GEV 两种分布模型得到统计2期1959—2016 年内的P=1%、2%的设计暴雨量，对比发现GEV2得到的设计暴雨量最大值分别比GEV模型所得结果小2.7%、0.08%，平均值分别小7.89%、6.18%，最小值小13.17%、12.4%。

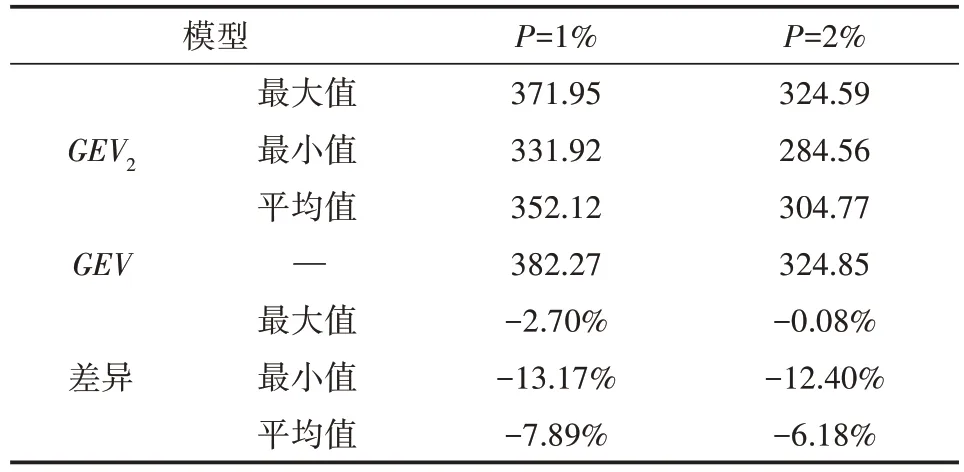
表2 GEV2与GEV分布模型在1959—2016年内的设计暴雨量对比

图5 为以GEV 模型成果作为设计值时每年的超越概率，如图5 所示，以GEV 模型求得P=1%、P=2%的设计暴雨量作为基准，采用GEV分布模型求2得对应的年超越概率呈现明显的减小趋势。以P=2%的设计暴雨值计算常规GEV模型的超越概率为2%，而适用性更好的GEV分布模型在工程寿命期2内（2017 年之后的50 年）计算该设计值对应的每年超越概率呈显著减少趋势，在工程使用期的初期每年的超越概率已经接近P=1%，在末期非常接近P=0.5%，差距达到了100%以上。

图5 以GEV模型成果作为设计值时每年的超越概率

3 结论与展望

本研究在暴雨资料不满足一致性假设推求设计暴雨时，构建了时变矩的GEV频率分布模型的多种形式，采用AIC 准则优选适用的时变矩GEV 频率分布模型，并将最优时变矩模型与常规的适用于一致性假设的GEV模型作对比，结论如下。

①在暴雨资料不满足一致性假设时，通过AIC准则表明，本研究构建的时变矩GEV2模型适用性优于常规的GEV频率分布模型，充分说明了时变矩模型在面对非一致性序列时的优越性。

②面对非一致性资料序列采用常规频率模型计算得到的设计值及其超越概率并不可靠，适用性更好的时变矩模型求解得到的设计值及其超越概率明显不同于常规频率分布模型。

③在面对不满足一致性假设的暴雨资料推求设计洪水时，应当对非一致性做处理，否则推求得到的设计洪水将产生较大的偏差，影响防洪安全和造成工程投资的浪费。

在采用时变矩GEV分布模型求解设计暴雨时，虽然该模型有一定的预测能力，但预测的准确程度还需要研究；不同的统计年限得到的设计值、超越概率也未必一致；如何使用统计年限使得具有预测功能的时变矩频率分布模型更可靠地推求设计值值得进一步的研究。