基于数值模拟的坝体泄洪消能研究

陈明昌

（民乐县抗旱防汛服务队，甘肃 民乐 734500）

0 引言

21 世纪以来，我国大坝建设进程逐步加快，且建设高度越来越高，特别是200 m 以上的高坝接连出现。由此以来，坝体泄洪消能产生的能量释放和传递时，势必会对周围环境和过流边界产生次生影响。截至目前，泄水建筑物遭受破坏的案例屡见不鲜，因此，坝体泄洪消能技术是大坝工程建设和良好运行的关键技术之一［1-2］。

重力坝的泄水构筑物通常由溢流表孔与底孔构成，前者具有泄流能力强、闸门运行调度灵活及安全性能高的特点；后者具有布设高程低且兼备水库防控功能而占优势。消能方式上，泄洪底孔常以挑流消能方式为主，如我国的三峡大坝［3］。采用该泄洪消能方式，在水力设计与运行方式上，较之于溢流表孔，面临更多的制约条件与技术挑战［4-5］，工程设计在实际施工前需要进行数值仿真模拟分析，以规避施工后造成不必要的损失。随着计算机的发展，数值模拟利用其建模快捷、成本低廉、时效性强等优点，受到研究人员的青睐［6-8］。

本研究以某混凝土重力坝为例，采用商用ANSYS 软件对设计与校核洪水位条件下泄洪洞泄流能力、断面流速等特性进行防洪安全分析。同时阐述了泄洪洞存在的安全问题及解决措施，提出最终的泄洪消能布置方案，可为同类工程设计提供参考。

1 数值模型及控制方程

1.1 模型建立

本研究数值模型采用ANSYS 软件进行建模模拟，详细尺寸及细节如图1 所示。计算域采用六面体结构网格，由于比较关注蓄水池产生的脉动对坝体的影响，因此，对该处进行节点加密。由于该模拟方案涉及FSI流、固耦合，因此需要建立流体计算域模型和固体计算域模型。

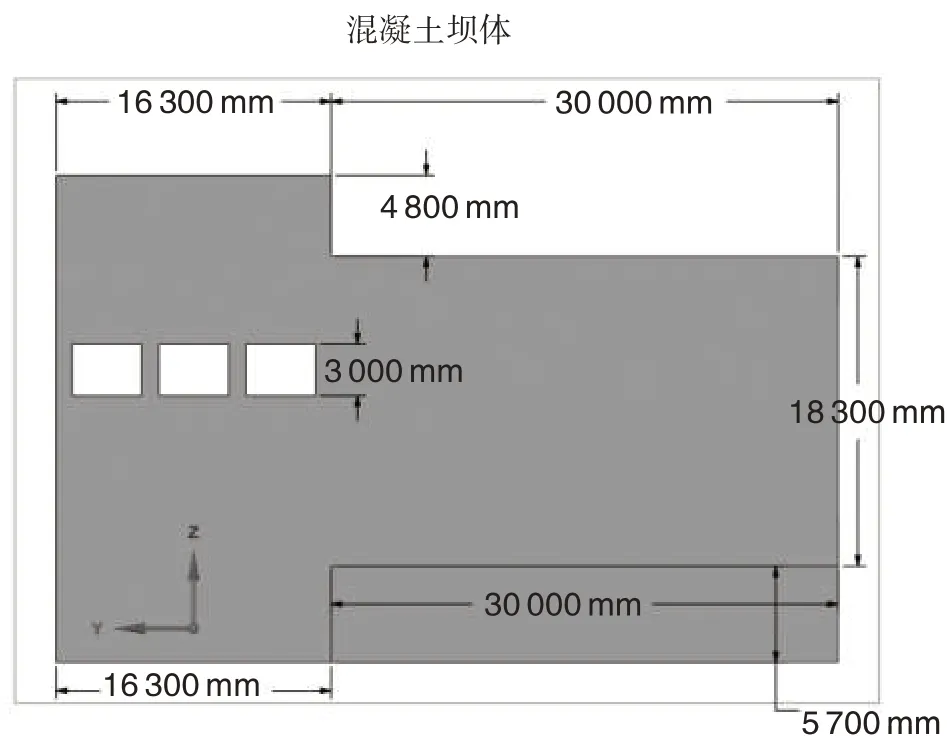
图1 三维模型建立示意图

1.2 控制方程

1.2.1 流体项控制方程。动量方程主要通过各相和属性来求得体积比率，如式（1）所示。

式中：t 表示时间，s；∇表示拉普拉斯算子；ρ 为流体密度，kg/m3；v 是流体速度矢量；μ 是动力黏度，N· s/m2；T表示温度，℃；g是重力加速度，m/s2。

能量方程如式（2）所示。

式中：keff为有效电导率，m/s；E为质量变量；P是流体压力，Pa；J→j,q为相间扩散通量；Sh是体积热源。

质量守恒方程如式（3）。

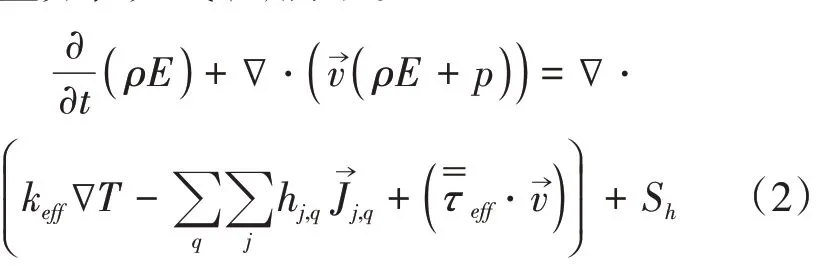
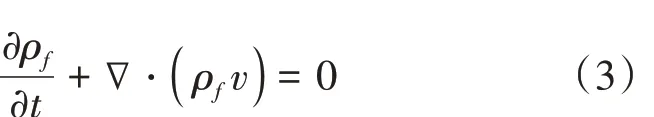
动量守恒方程如式（4）。

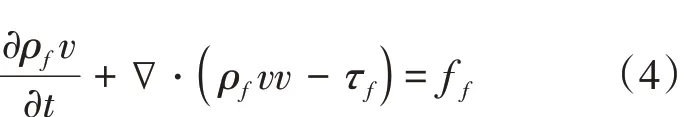
以上式中：ff是体积力矢量；v 是流体速度矢量；ρf是流体密度，kg/m3；τf是剪切力张量（如式5）；t表示时间。

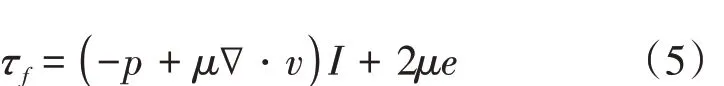
1.2.2 固体项控制方程。固体部分的守恒方程可以由牛顿第二定律导出，如式（6）：

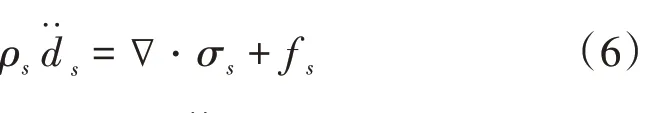
式中：fs是体积矢量；ds 是固体域的当地加速度矢量；ρs是固体密度；σs是柯西应力张量。

2 结果分析

数值模拟分析分为以下两种工况。

工况1：当坝前水位为正常蓄水位1 410.00 m时，排沙底孔开1 孔且下游无水时，设计流量为131 m³/s。

工况2：当上游设计洪水位为1 410.96 m，下游设计洪水位为1 389.50 m 时，排沙底孔全开，过闸流量为406 m³/s。

2.1 不同工况泄水建筑物的水力参数模拟

如图 2、图 3 所示，模拟了工况 1 总计 10 s 时刻的流态、流量图。T=4 s 前，水流全部集中在库体上部，水流不是很平稳，看不出有规律的流向；流量呈现波动上升的趋势，T=4 s 时流量达102 m3/s，T=5 s时，出流量达到最大流量123 m3/s。T=6 s 时，闸孔开始出流，由于能量基本消耗在水跃部分，排沙底孔的出流流态较为平缓，此时流量减小至118 m3/s。T=8 s 时，水流流态继续保持平稳状态；T=10 s 时，随着下泄流量的增大，排沙底孔下游的水面波动较大；随后，流量已经趋于平缓，且保持稳定出流，流量为99 m3/s。

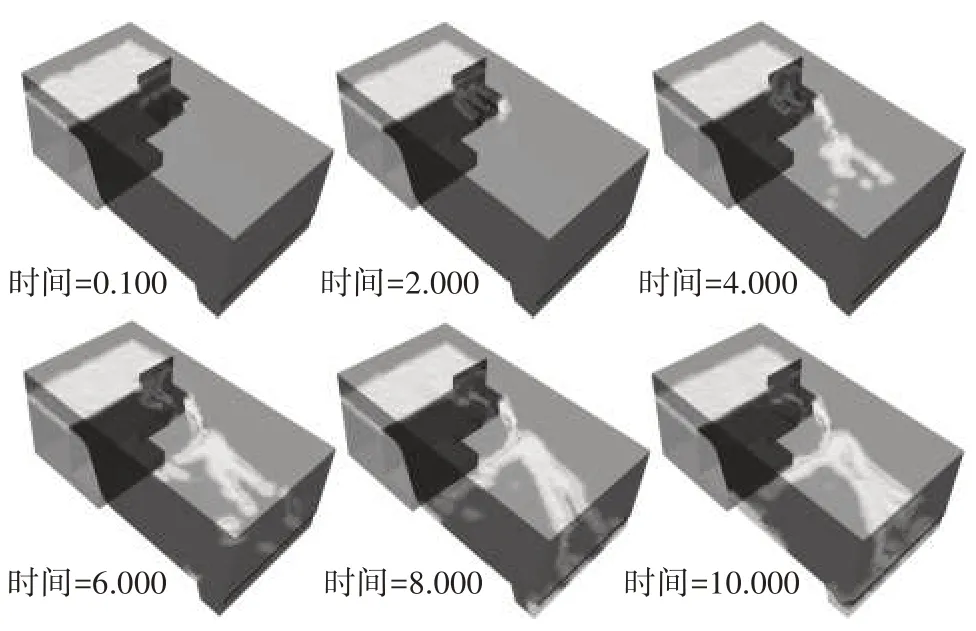
图2 工况1流态模拟云图

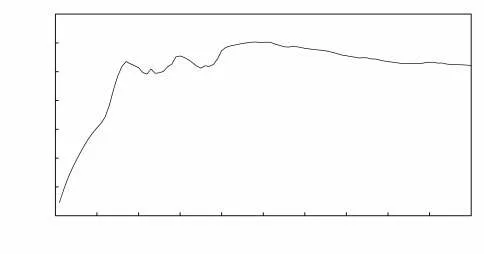
图3 工况1流量模拟曲线

总体来看，T 为0～10 s 时，流量呈现波动增大的趋势，最终趋于稳定出流。闸孔出口处没有非常明显的水跃发生，出口水流平稳，所以，闸孔出水的水舌与下游水面衔接自然。由于蓄水池的存在，闸孔出流附件并未发生旋滚区，因此，改善了排沙底孔出口的紊动条件。

如图4、图5所示，模拟了工况2总计15 s的流态、流量变化曲线。3孔排沙孔全部打开时，T=3 s，水流进入后，泄流量呈现急剧增加趋势，约为105 m3/s。T=6 s，随着下泄流量的增大，由于过水断面的收缩，导致水面跌落，流量为400 m3/s。T=9 s 后，流态区域稳定出流，此时最大流量为450 m3/s。池内水流略呈淹没射流流态，水舌两侧存在对称旋涡，沿垂直向下方向观测，左侧形成逆时针旋涡，消力池底部边墙前部水流存在大量气泡。随着下游距离的增加，流量呈现缓慢减小趋势（见图4），保持在395 m3/s，侧面说明消力池的消能效果明显。

图4 工况2流态模拟云图

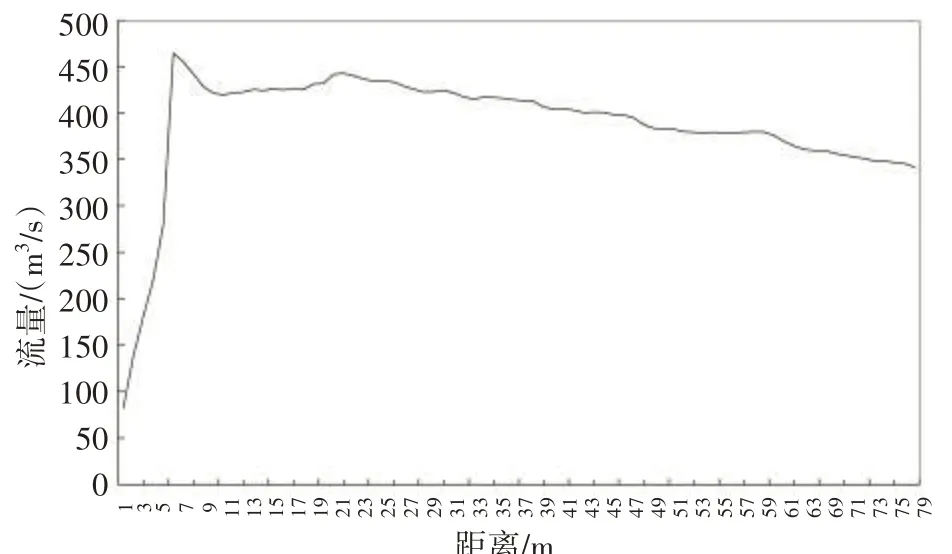
图5 工况2流量模拟曲线

如图5 所示，排沙底孔全部打开时，随着库水位的升高，泄流量增大。在闸室的上下进口处，变化各不一样。水流进闸后，由于过水断面收缩，导致水面跌落，跌落的最低点大约流量差为400 m3/s。排沙底孔全部打开时，每个孔的出流随着流量的不同，池内的水流表现出不同的流量状态。Q=260 m3/s时，池内为自由射流流态，形成明显的底部射流区，因而使得扩散水流在两侧边墙的作用下，形成纵向水翅并与水舌互相碰撞，使得动能损失增加。Q=450 m3/s，相比上一阶段，池内水流淹没不明显，水舌两侧漩涡对称存在，水面波动较小且池内水位呈现平稳。由此看出，随着流量的变化不同，分别呈现自由射流、略淹没射流和淹没与略淹没的临界流态。

如图6、图7 所示，为了详细分析泄水建筑物流速场的变化规律，在排沙底孔开1 个的一定范围内布置了流速量测点A。数值模拟中，网格数量的多少决定了计算成本的大小，由于上游水位较深，将出口流速监测点布置在A 位置。由此发现，如果上游水位不变，底孔过流对堰面的流速不会造成影响；相反，上游水位变化，堰面流速也变化，且随着水位的升高，堰面流速呈现增大的趋势。总体而言，在水平溢流段堰面的流速分布均匀；自由下泄段流速呈现逐渐增大趋势，符合急变段的流速变化规律。然而，靠近反弧段底部，流速约高达14.86 m/s。

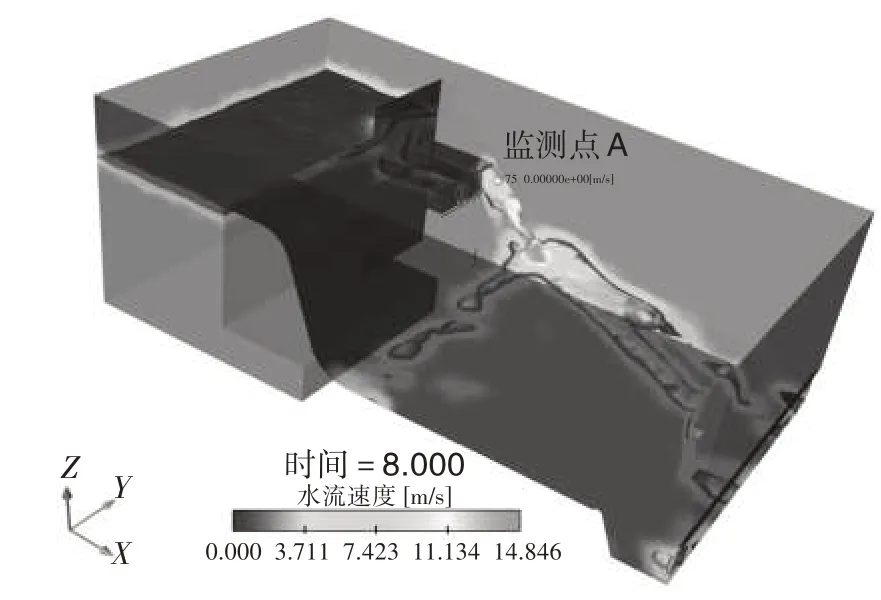
图 工况（开 孔）泄流时的流速变化模拟云图

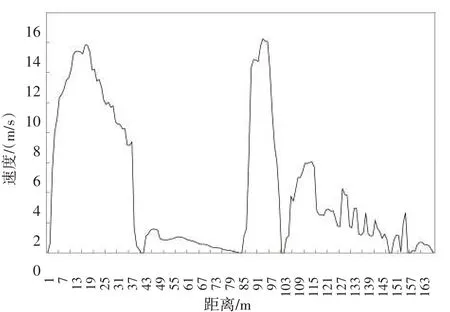
图7 工况1（开1孔）泄流速度的曲线变化

如图8所示，选取监测点B，测量排沙底孔全开时的流速分布。在敞泄情况下，排沙孔进口断面表面流速大于底流速，该断面最大表面流速为12 m/s。进入孔口后，平均流速在逐渐减小。在消力池处，最大表面流速为8 m/s。

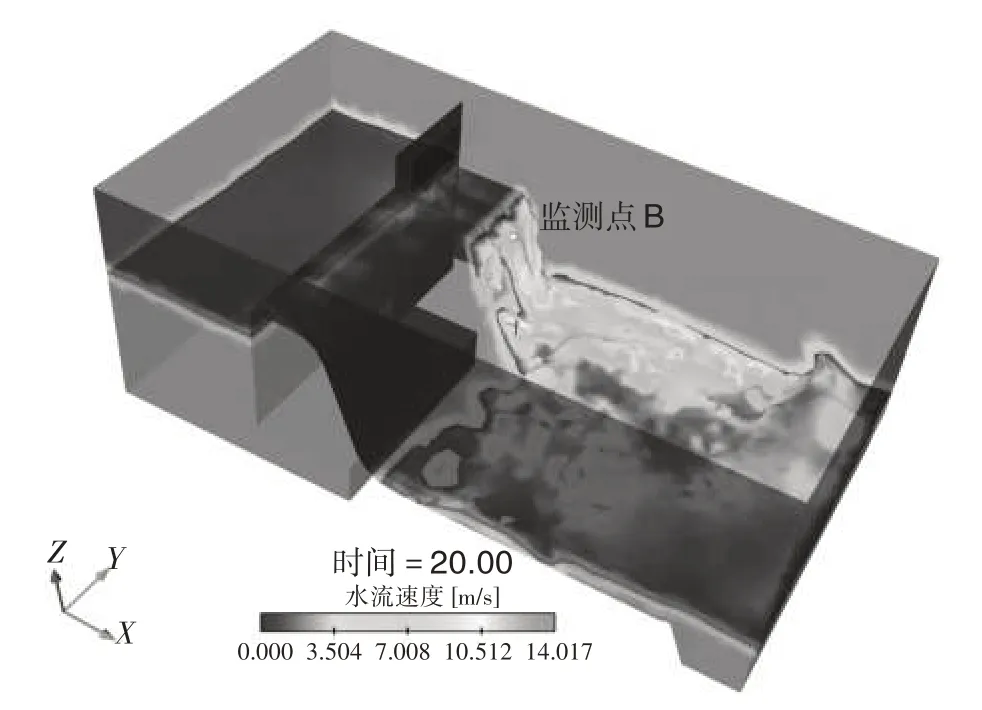
图8 工况2（孔全开）泄流时的流速变化模拟云图

如图9所示，随着3孔出水量的变化可以看出，流速呈现波动式变化，主要原因是泄洪时坝体蓄水池脉动效应所致。其余同工况1 的情形，堰面流速随着水位的变化而变化，水位上升，流速则增大。水平溢流段的流速仍然分布较为均匀；自由下泄段流速呈现增大趋势，符合急变段的流速变化规律。反弧段底部位置的流速变化规律亦然。在挑坎末端流速逐渐减小。当上游水位不变时，上游堰面流速保持不变，不因下游水位的变化而改变。当下游水位相比鼻坎高时，由于回流的出现，反弧段流速呈现逐渐减小趋势。

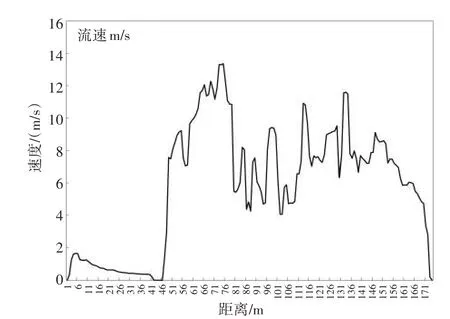
图9 工况2（底孔全开）泄流速度的曲线变化

2.2 不同工况坝体稳定性分析

如图10、图11 所示，分别模拟了工况1、工况2的坝体应力极值云图。对于工况1 而言，从仿真计算的云图分析可知，其应变的最大值和最小值分别在坝体排沙孔附近，最大值为0.000 195 2 m，最小值为0.000 006 5 m，其应变的极值均小于设计值，完全符合设计规范。应力的极大值为395 000 Pa，均发生在排沙孔过水时，坝体的应力最大值仅为19 561 Pa，设计报告提供的参数为混凝土的允许应力8.5 MPa，而且该值是正常蓄水位、冰冻期及发生地震时均满足要求，换言之，仿真计算的结果远远小于设计规范值。坝体位移的极大值发生在蓄水池产生脉动效应时的上方坝体，从仿真计算的云图来看，最大值仅为0.000 325 m，符合坝体抗滑设计，在合理范围内。

图10 工况1的坝体变形极值云图

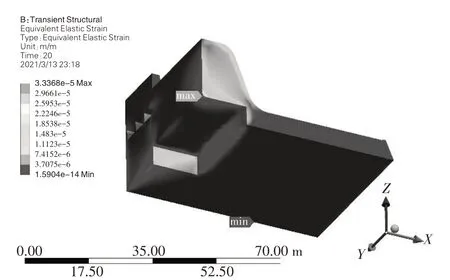
图11 工况2的坝体极值云图

对于工况2而言，从仿真计算的云图分析可知，即使3孔全开，蓄水池发生脉动效应，其应变的最大值和最小值分别在蓄水池靠近排沙孔附近的坝段以及排沙孔附近，最大值为0.000 174 6 m，最小值为0.000 008 7 m，其应变的极值均小于设计值，完全符合设计规范。应力的极大值为665 000 Pa，发生在蓄水池右侧顶上方，最小值几乎忽略不计，此处不再赘述，设计报告提供的参数为混凝土的允许应力8.5 MPa，而且该值是正常蓄水位、冰冻期及发生地震时均满足要求，换言之，仿真计算的结果远远小于设计规范值。坝体位移的极大值发生在蓄水池产生脉动效应时的蓄水池两侧边墙，从仿真计算的云图来看，最大位移值仅为0.000 011 23 m，符合坝体抗滑设计，在合理范围内。

3 结语

本研究通过ANSYS 软件对不同工况泄水的流量、流速、流态及蓄水池对坝体的稳定性等方面进行了分析。结果表明，高速水流产生的脉动对坝体应力各个位置的值均小于1 MPa，高速水流产生的脉动闸体应力较大值主要集中在上下游闸墩与闸室底板的连接点处，数值大约在4.425 MPa。排沙孔底孔全开时，闸体与边墙连接处的受力最大，最大应力为0.000 1 MPa。泄洪时坝体产生最大位移的位置在坝体泄水口附近，模拟计算分析产生的最大位移较小，仅为0.62 cm，沿x 方向的应力最大值为1.6×106kPa，最大塑性应变值为5.5×10-5m/m，不会破坏和损坏坝体结构；上述模拟结果均符合设计规范。因此，本研究构建的数值模型可以为实际工程设计提供科学的数据支撑，也可为同类实际工程设计提供参考。