基于PBFT算法改进的去主节点共识机制优化
董德宝,王云光
(1.上海理工大学 健康科学与工程学院,上海 200000;2.上海健康医学院 医疗器械学院,上海 200120)
0 引言
拜占庭容错算法BFT最早由Pease和Lamport在20世纪80年代提出[1],它是依据节点之间相互发送消息来达成共识协议,此协议的时间复杂度为指数级,现实中并未得到大量普及应用。1999年Miguel Castro和Barbara Liskov提出 了实用拜占庭容错算法(Practical Byzantine Fault Tolerance,PBFT),解决了原始BFT算法的信息传输复杂度太高的问题,由此实用拜占庭容错算法在实际系统中变得可行[2]。PBFT算法成功实现将BFT算法的时间复杂度从指数级降低到多项式级别[3],在实际应用中得到普及,但是该算法对节点的共识一致要求较高,更加适合私有链和联盟链[4]。
1 PBFT共识协议
1.1 PBFT算法共识流程
实用拜占庭容错算法由五个共识阶段组成,分别为请求阶段(request)、预准备阶段(pre-prepare)、准备阶段(prepare)、提交阶段(commit)、反馈阶段(reply),如图1所示。

图1 PBFT算法共识流程
1.2 PBFT算法共识详情
请求阶段:主节点(primary)接收来自客户端(cilent)的请求信息,主要验证客户端的签名是否正确(若正确,则请求成功;否则,请求失败),并将信息打包成格式为 预准备阶段:主节点(primary)将接收到客户端的正确请求信息,按照请求号的先后顺序依次分发给副本节点(replica),并将信息打包成格式为< 准备阶段:从节点(replica)收到主节点(primary)的预准备消息后,首先,验证预准备消息的真实性,验证通过再将预准备消息和准备消息打包发送给剩余从节点,并将相应信息写入日志文件,其信息的打包格式为 提交阶段:所有的节点(主节点和从节点)将所有确认过的消息广播给其他节点,其信息的格式为 反馈阶段:客户端会接受来自节点的共识结果反馈,当接收到(f+1)个确认消息后,则系统达成共识,每个节点的发送信息格式为 由于PBFT共识算法的主节点仅有一个且选取随意,它负责对客户端的请求进行排序[4],每个请求打上需求号标记,在接下来的区块打包过程中,按照需求号从低到高的顺序进行处理,并将主节点收到的信息广播给其他从节点。由于随意选取主节点,有概率选择的主节点为拜占庭节点,在经过五轮算法共识后,结果不一致,就会触发视图转换(view-change)机制,更换下一个节点(也有可能为拜占庭节点)作为主节点,无法防止主节点作恶,这种情况下就增加了网络开销和通信时延,使算法的效率下降。 笔者通过阅读大量文献发现,很多学者将选取主节点为主要方向,引入积分制、可信列表、随机函数、门限签名等优化主节点选取机制。本文提出无主节点共识算法(NO-PRIMARY PBFT,简称N-P PBFT)思路,即将主节点负责的客户端需求按序处理,并将客户端信息分发给从节点的处理过程置于共识算法之外,由客户端负责“担任”主节点,客户端将以时间戳先后顺序处理业务请求,其N-P PBFT共识算法的流程如图2所示。 N-P PBFT共识算法在原来PBFT共识算法的基础上省去了选取主节点的流程,采用无主节点共识流程,其具体分为:处理阶段(dispose)、准备阶段(prepare)、提交阶段(commit)、回复阶段(reply)、分发阶段(distribute),如图2所示。 图2 NP-PBFT算法共识流程 处理阶段:引入外部服务(extra-service)用来接收和处理客户端请求,按照时间戳将需求分配任务号依次处理请求,并将信息打包成格式为 准备阶段:将外部服务处理好的需求,依次发给参与共识的所有区块节点,并将信息打包成格式为< 提交阶段:所有的节点将所有确认过的消息广播给其他节点,其信息的格式为 反馈阶段:客户端会接受来自节点的共识结果反馈,当接收到(f+1)个确认消息后,则系统达成共识,其每个节点的发送信息格式为 分发阶段:客户端接收到参与共识的节点的结果反馈后,通过外部服务判断接收到共识的消息个数是否大于(f+1)个,若满足,则认为本次共识过程成功达成,反之,共识失败。 本课题采用的操作系统为MICROSOFT WINDOWS 11专业版、版本为10.0.22000 BUILD 22000、类型为X64-BASED PC、处理器为INTEL64 FAMILY 6 MODEL 142 STEPPING 10 GENUINEINTEL~1801 MHZ的PC电 脑,通 过JavaScript程序实现。 在PBFT算法中,假设算法性能测试的总节点个数为d(d≥3,d∈N*),当主节点为拜占庭节点则会进行视图转换,新增的通信次数为d(d-1),假设发生视图转换的概率为q,并模拟存在一个拜占庭节点的情况下开展算法性能测试,PBFT算法的通信时间复杂度为O(N2),其中PBFT算法在完成一次完整共识(五个阶段)的过程中的总通信次数SUMPBFT为: N-P PBFT算法中,为保证测试条件的一致性,假设算法性能测试的总节点个数为d(d≥3,d∈N*),在SUMN-PPBFT算法中,无主节点参与共识,故不会存在主节点故障或者为拜占庭节点时发生视图转换协议概率,同时模拟系统中存在一个拜占庭节点的情况下开展算法性能测试。在处理阶段和分发阶段由外部服务处理和分发客户端信息,不参与算法共识流程,故参与共识的阶段为准备阶段,其通信次数为d;在提交阶段,其通信次数为(d-1)(d-1);在反馈阶段,其通信次数为d-1。故N-P PBFT算法在完成一次完整共识的过程中的总通信次数SUMN-PPBFT为: 对比两种算法的通信开销性能,本次实验采用参与共识流程的节点总数以4,10,16,22,28为例,分别计算两种算法下的通信开销次数,如表1所示。 表1 两种算法的通信开销次数 通过对比PBFT和N-P PBFT算法的通信开销性能(如图3所示),当参与共识的系统节点总数为4个时,两种算法的通信开销分别为22次和16次,通信次数相近,但是随着系统中节点数的增加,可以看出N-P PBFT算法的通信开销相对PBFT算法有了显著的优化。 图3 两种算法的通信开销对比 根据PBFT和N-P PBFT算法在同一假设条件下的通信,可以看出其通信时间复杂度都是O(N2),但是PBFT算法可能存在主节点故障或者瘫痪,触发视图转换协议增加通信次数,而N-P PBFT算法提出无主节点共识算法流程能够完全避免PBFT的主节点相关问题。为了更加明显地看出两种算法在通信性能上的差异,两种算法的单次通信开销比б(overhead traffic)=SUMPBFT/SUMN-PPBFT,计算公式如下: 同样,本次实验采用参与共识流程的节点总数以4,10,16,22,28为例,分别计算当q=0和q=1时两种算法下的通信开销次比,如表2所示。 表2 两种算法的单次通信开销比 通过将PBFT与N-P PBFT算法的通信开销进行对比,在图4中可以看出其бcommunicationtimesratio值恒大于1,同时,考虑到PBFT算法可能会发生视图转换的概率q,本次实验采取了q=0和q=1两种情况,q=0即主节点是正常节点,未发生视图转换;q=1即主节点故障或者为拜占庭节点,从而会发生视图转换,导致PBFT算法中通信开销增加。考虑到现实的一般性,现实中的бcommunicationtimesratio在图4中表现位于бcommunicationtimesratio(q=1)和бcommunicationtimesratio(q=0)之间,本次实验采取两种极端情形。从图4可以看出,当q=0时,бcommunicationtimesratio值恒大于1,可以看出随着节点数的增加,бcommunicationtimesratio值也会呈现正相关,说明N-P PBFT对优化算法的通信开销有较大的提升。 图4 两种算法的单次通信开销比 为了更明显地看出两种算法通信开销比的相对差异和N-P PBFT算法相对于PBFT算法的优化量化数据,假设在没有遇到视图转换协议的情况下,即q=0,采用ψ表示累计通信开销比,其计算方法为d∈N*),详细的计算公式如下: 同样,本次实验采用参与共识流程的节点总数以4,10,16,22,28为例,分别计算当q=0时两种算法下的累计通信开销次比,如表3所示。 表3 两种算法的累计通信开销比 由两种算法的累计通信开销比(见图5)可以看出,随着系统节点数的增加,累计通信开销比ψsumcommunicationoverhead呈现类似一次函数趋势增长,k值约等于0.684,在假设PBFT算法没有发生视图转换的情况下(q=0),PBFT算法的通信次数最小。从图5可以看出累计通信开销比ψsumcommunicationoverhead的增长趋势,由此可以得出N-P PBFT相对于PBFT算法的性能得到进一步优化。 图5 两种算法的累计通信开销比 通过优化传统的PBFT算法,在原有算法达成一致性共识流程中,引入外部服务担任主节点角色,避免在选取主节点时带来的一定概率选中拜占庭节点或者节点宕机情形,从而触发视图转换协议,增加一致性共识阶段的通信开销,改善了原有五个阶段的共识方式,有效降低了通信次数,通过最终实验对比发现,N-P PBFT相对于PBFT算法在通信复杂度都为O(N2)的基础上,在实验设置的假设条件中,N-P PBFT有效降低了原有算法的通信开销,系统的算法共识一致性效率得到明显提升。2 PBFT算法优化及设计
2.1 PBFT算法的不足
2.2 N-P PBFT算法思路
2.3 优化的PBFT算法设计

3 N-P PBFT与PBFT算法实验对比
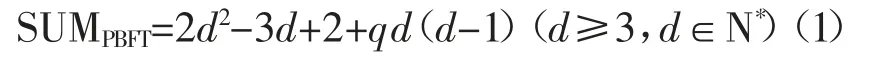









4 结语

