基于最粗优势木胸径生长的湖南栎类天然林立地质量评价模型*

何 静 李新建 朱晋梅 朱光玉

(1.中南林业科技大学林学院 长沙 410004； 2.国家林业和草原局中南调查规划院 长沙 410004； 3.湖南省林业局 长沙 410001)

立地生产力指一个特定林分生产地上林木的潜力，是林地和林分共同形成的生产单位(Skovsgaardetal.， 2008)。立地生产力评价是判断或预测立地适宜性或潜在生产力的一项基础性工作，在森林科学经营中具有重要作用(Berrilletal.， 2013)。森林立地生产力评价指标可归纳为林分高、林分蓄积或断面积生长量、林分特征和立地属性4类(朱光玉等， 2016)，基于4类评价指标产生了多种评价方法，其中以地位指数评价最为常用，即以某树种林分基准年龄时的优势平均高作为衡量森林立地生产潜力的指标(Fonwebanetal.， 1995； 孟宪宇， 2006)。

野外实地调查时，尤其在林区中，由于地形十分复杂、坡度变化较大、林木生长状况和林分密度不同等因素，给树高的准确测定带来了很多困难，而林木胸径与和树高之间存在密切关系(Sharmaetal.， 2007； Leietal.， 2009； 王冬至等， 2016； 2019； 段光爽等， 2020)，且胸径测量非常准确，因此，一些学者以优势木胸径为指标，通过构建模型或采用地位级法对林分生长与立地质量评价进行研究： 如应用多期胸径-年龄数据编制胸径立地指数表，用于天然林立地质量评价(刘洵等， 2019)； 应用树木理论生长方程，以优势木平均胸径为指标，导出立地指数模型，从理论和技术上解决立地质量评价问题(李铁华等， 1997)； 以最大胸径生长率为指标建立的杉木(Cunninghamialanceolata)人工林立地质量评价数量化理论模型，不仅可以评估现有杉木人工林的生产力，而且能够预测非林地的潜在生产力(杨海宾等， 2020)。可见，应用胸径-年龄构建立地指数模型评价立地质量是可行的(李振芳等， 2016； 吴恒等， 2015； 马炜等， 2013)。

混合效应模型是一种常用的处理局部变异性的建模方法，可在模型中反映其他因子的作用，针对不同立地类型，混合效应模型能够根据混合效应参数构建优势木胸径生长曲线簇，从而反映立地类型对胸径生长的影响程度(Fangetal.， 2001； Calamaetal.， 2004)。而且，混合效应模型既可以反映个体之间的差异，也可以反映总体的平均变化趋势，利用混合效应构建多行立地指数曲线能够提高立地指数估计精度(Calegarioetal.， 2005； 符利勇等， 2013； Zhuetal.， 2019)。

栎类(Quercus)天然林是我国天然林的主要林分类型，作为一种阔叶用材林在湖南林业生产中发挥了重要作用(胡芳名等， 2000)。天然林经营管理相对复杂，天然混交林立地质量评价仍是当今世界林业研究的难点和焦点，对天然林生产力预估和评价研究非常必要。鉴于此，本研究以湖南栎类天然林为研究对象，采用数量化方法Ⅰ筛选对优势木胸径生长影响显著的立地因子，通过混合效应、k-means聚类构建含立地类型的优势木胸径生长模型，导出以最粗优势木胸径为指标的基于立地分级的湖南栎类天然林立地质量评价模型，以期为天然林立地质量评价提供一种新方法。

1 研究区概况

湖南位于长江以南，属长江中游地区，地处108°47′—114°15′E，24°38′—30°08′N，为大陆性亚热带季风湿润气候，年均气温15～18℃，年降水量1 200～1 700mm。土壤以黄壤和黄棕壤为主。植物资源丰富，包括青冈栎(Cyclobalanopsisglauca)、栲(Castanopsisfargesii)、银杏(Ginkgobiloba)、南方红豆杉(Taxuschinensis)、水杉(Metasequoiaglyptostroboides)等珍贵树种。

2 数据与方法

2.1 数据采集

在湖南五盖山林场、八大公山自然保护区、平江县芦头实验林场等5个地点，设置20 m×30 m栎类天然林固定样地51块，对样地内胸径大于5cm的活力木进行每木检尺，调查因子包括胸径、树高、海拔、坡度、坡位、坡向、土壤类型等。对样地数据进行预处理，选取每块样地的最粗优势木，并利用生长锥钻取年龄(AGE)。林分因子统计见表1。

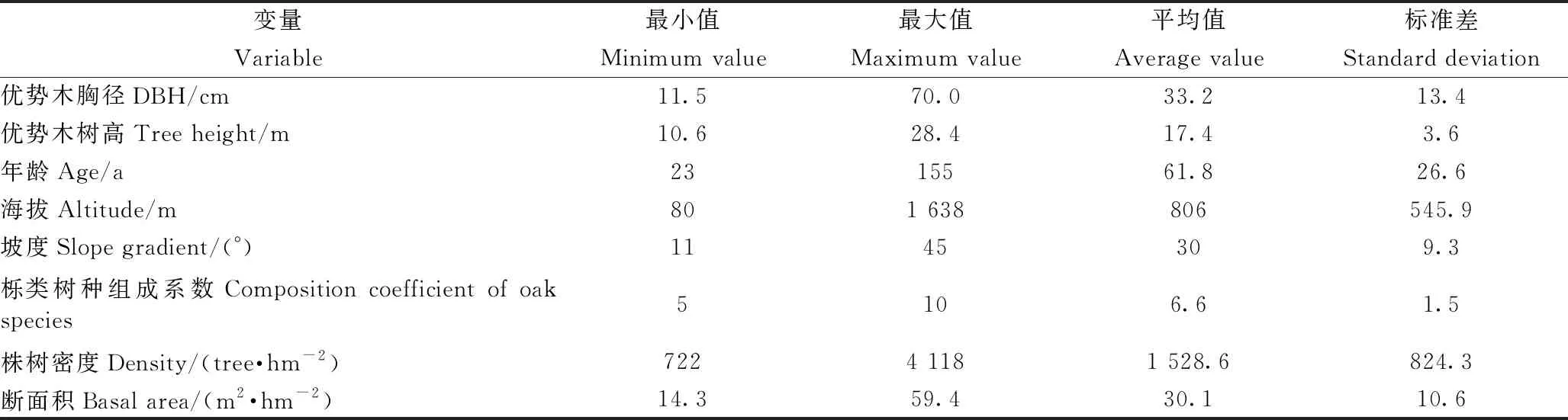
表1 林分因子统计

2.2 研究方法

2.2.1 数量化方法 Ⅰ筛选因子 数量化方法Ⅰ指自变量中包含定性变量的回归模型，表达式(周光亚等， 1979)如下：

(1)

式中：yi为变量y在i样品中的观测值；bjk为j项目k类目的得分；εi为随机误差。

运用Forstat 2.2“统计之林”软件进行数量化方法Ⅰ分析，筛选可能影响栎类天然林优势木胸径生长的因子。

2.2.2 基础模型拟合与选择 选取4种常见的树木理论生长方程，分别对栎类天然林最粗优势木胸径与年龄的相关关系进行拟合，候选基础模型名称、表达式和参数见表2，通过一系列评价指标，确定最符合栎类天然林最粗优势木胸径生长的最优基础模型。

2.2.3 立地分类 为方便划分立地类型和建立模型，将海拔、坡度、坡向、坡位和土壤类型5种立地因子进行分级处理，分级标准见表3。

2.2.4k-means聚类 应用k-means聚类划分立地类型。k-means算法实质上是一种将聚类视为密度估计问题的概率方法，假设样本来自于如下形式的混合模型(雷小锋等， 2008)：

p(x|θ)=∑j=1∶kP(Cj)pj(x|θj,Cj)。

(2)

式中：θ=(θ1,…,θk)为待估计的参数向量； 条件概率密度pj(x|θj,Cj)称为分量密度，表示类别j的概率密度形式，且参数向量θj未知； 先验概率P(Cj)称为混合因子。

表2 候选基础模型拟合结果①

①D为最粗优势木胸径(cm)，AGE为最粗优势木年龄(年)，a、b、c为模型待求参数。Dis the diameter at breast height (cm) of the thickest dominant tree, AGE is the age (year) of the thickest dominant tree,a,bandcare the parameters to be calculated in the model.

表3 调查因子等级划分

2.2.5 混合效应模型构建 混合效应模型(mixed effect models， MEMs)是根据回归函数依赖于效应参数的非线性关系建立的数学模型，其中，效应参数包括固定效应参数和随机效应参数，其一般形式(符利勇等， 2020)如下：

Yi=f(β,μi,Xi)+εi。

(3)

式中：Yi和Xi分别为第i个立地类型的因变量和自变量向量；εi为误差向量；β、μi分别为固定效应参数和随机效应参数。

2.2.6 模型评价与检验 采用赤池信息量(Akaike information criterion, AIC)、贝叶斯信息量(Bayesian information criterion, BIC)、确定系数(determination coefficient,R2)、平均绝对误差(mean absolute error, MAE)和均方根误差(root mean square error, RMSE)评价模型，指标计算公式如下:

AIC=-2lnl+2p;

(4)

BIC=-2lnl+lnn×p;

(5)

(6)

(7)

(8)

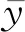
3 结果与分析

3.1 立地因子筛选

林分最粗优势木胸径生长受多种立地因子影响，根据最粗优势木胸径与不同立地因子的关系，采用数量化方法Ⅰ对其进行显著性分析，结果(表4)表明，对优势木胸径生长影响显著的立地因子包括海拔、坡度、坡向和坡位，显著性顺序为海拔>坡度>坡向>坡位。

3.2 基础模型拟合与选择

基于栎类天然林51块样地实测数据，分别以最粗优势木胸径和年龄为因变量和自变量，构建林分最粗优势木胸径生长基础模型，采用表2中的基本理论生长方程通过R语言的nls函数拟合最粗优势木胸径和年龄的相关关系。由表5可知，4种理论生长方程的确定系数(R2)均在0.7左右，其中Richards模型的拟合效果最好，R2为0.7318，平均绝对误差(MAE)和均方根误差(RMSE)分别为5.4426和6.8791，故本研究选择拟合效果最好的Richards模型为最粗优势木胸径生长基础模型(M4)。

表4 立地因子显著性检验①

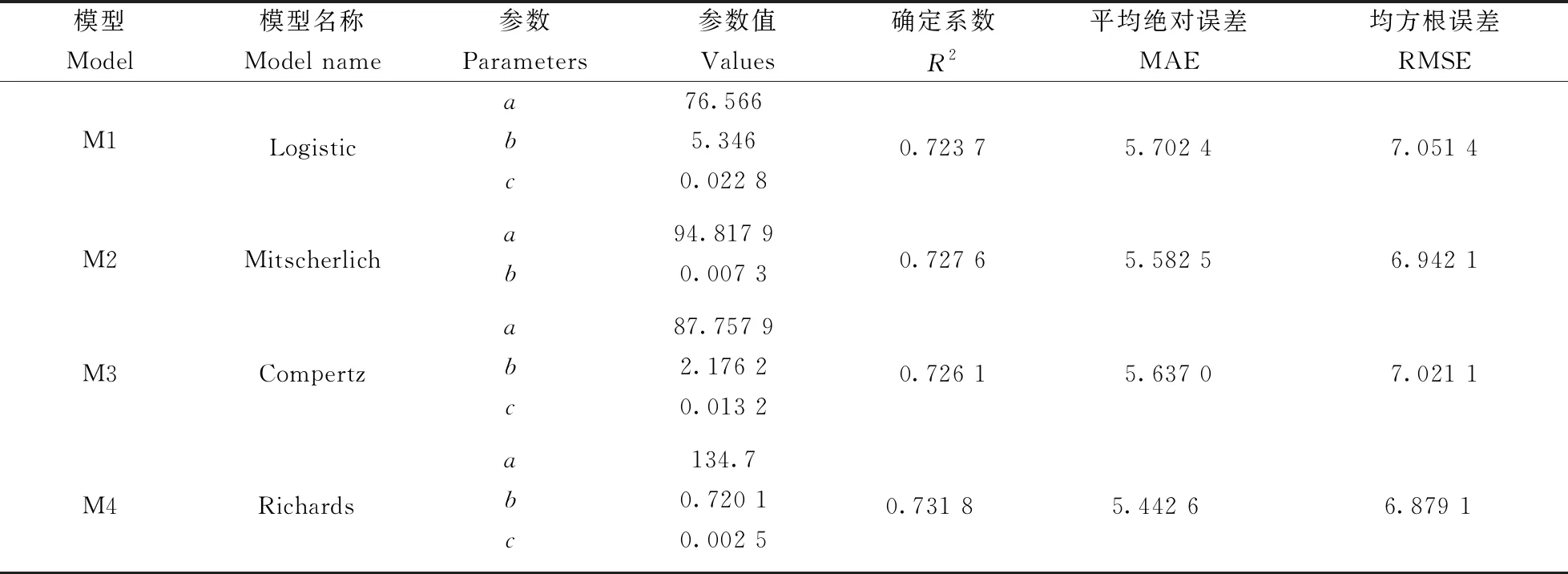
表5 基础模型拟合结果

3.3 基于立地类型效应的非线性混合效应模型构建与分析

不同立地条件下，林分最粗优势木胸径生长可能存在差异，故将海拔、坡度、坡向和坡位按标准(表3)分级、组合构成720种初始立地类型，具体划分情况见表6。

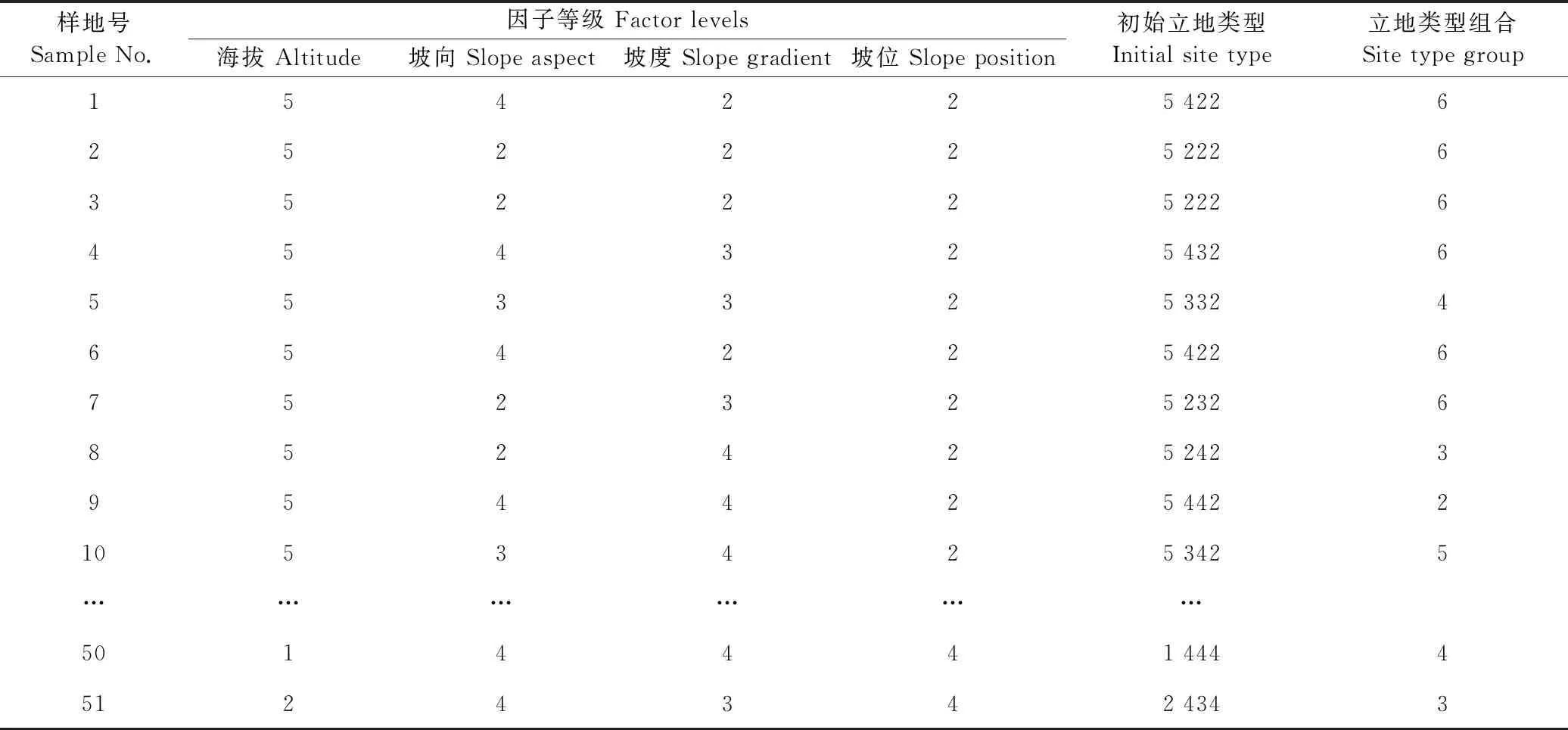
表6 初始立地类型与立地类型组合划分

本研究只用到初始立地类型中的38种，将组合后的初始立地类型作为随机效应加入基础模型构建混合效应模型，模型拟合结果(表7)显示，只在参数a上收敛，含立地类型随机效应的栎类天然林立地指数模型表达式为：

D=[a+μi)×(1-exp(-c×(AGE)]^b+ε。

(M4.1)

式中：a、b、c为模型参数；μi为随机效应参数；D为林分最粗优势木胸径； AGE为林分最粗优势木年龄；ε为误差项。

混合效应模型的R2相比基础模型有所提高，由原来的0.7318升至0.9016，含立地类型的混合效应模型明显优于基础模型。

残差分布是模型异质性检验最直观的工具之一，对基础模型M4和混合效应模型M4.1的拟合结果进行残差分析(图1)可知，模型残差均呈随机分布，且M4.1残差分布更为集中、均匀，可见混合效应能够提高模型精度。

表7 混合效应模型拟合结果

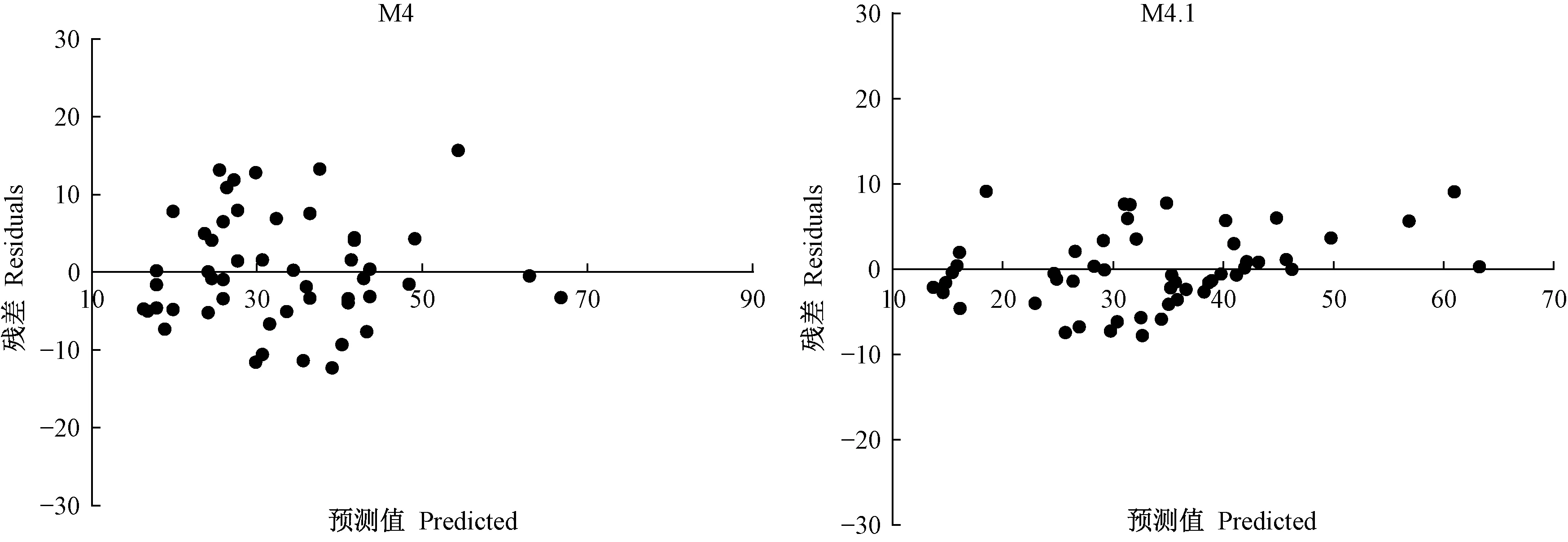
图1 基础模型M4和混合效应模型M4.1残差分布

3.4 基于立地类型聚类的非线性混合效应模型构建与分析

不同初始立地类型下，最粗优势木胸径生长状况不同，生长过程存在差异。本研究51块样地共有38种初始立地类型，为简化初始立地类型数量，将模型M4.1拟合得到的a参数值应用k-means聚类，在满足生长规律的基础上，以聚类精度≥95%为标准，将影响效果相近或相同的初始立地类型聚类成立地类型组。由表8可知，当聚类成6个立地类型组时，精度达96.4%，满足精度要求。

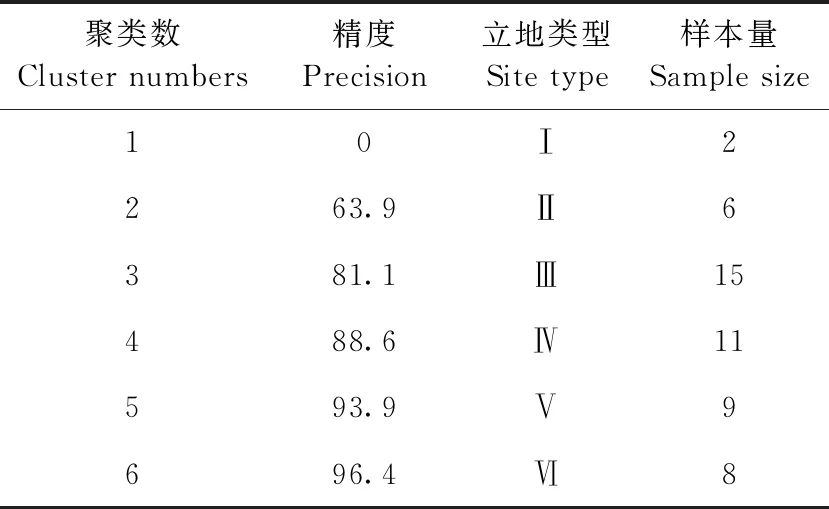
表8 立地类型聚类结果

将聚类后的立地类型组作为随机效应加入最优基础模型构建含立地类型组的混合效应模型(M4.2),由表9可知，与基础模型M4相比，M4.2的AIC、BIC均有所减小，Loglik有所上升；R2从0.7318升至0.9269，拟合精度提高26.7%，说明聚类后的立地类型组对栎类天然林最粗优势木胸径生长影响显著。模型M4.2的表达式为：

Dj=aj×[1-exp(-c×AGE)]^b+ε。

(M4.2)

式中：Dj为第j个立地类型组的最粗优势木胸径；aj为第j个立地类型组的参数值；b、c为模型参数；ε为误差。

表9 模型M4.2的精度评价与参数估计

对模型M4.2的拟合结果进行残差分析(图2)可知，模型残差在横坐标上下浮动，与图1对比，分布更加集中、均匀，说明立地类型组作为随机效应加入模型能够有效改进残差，提高模型精度。

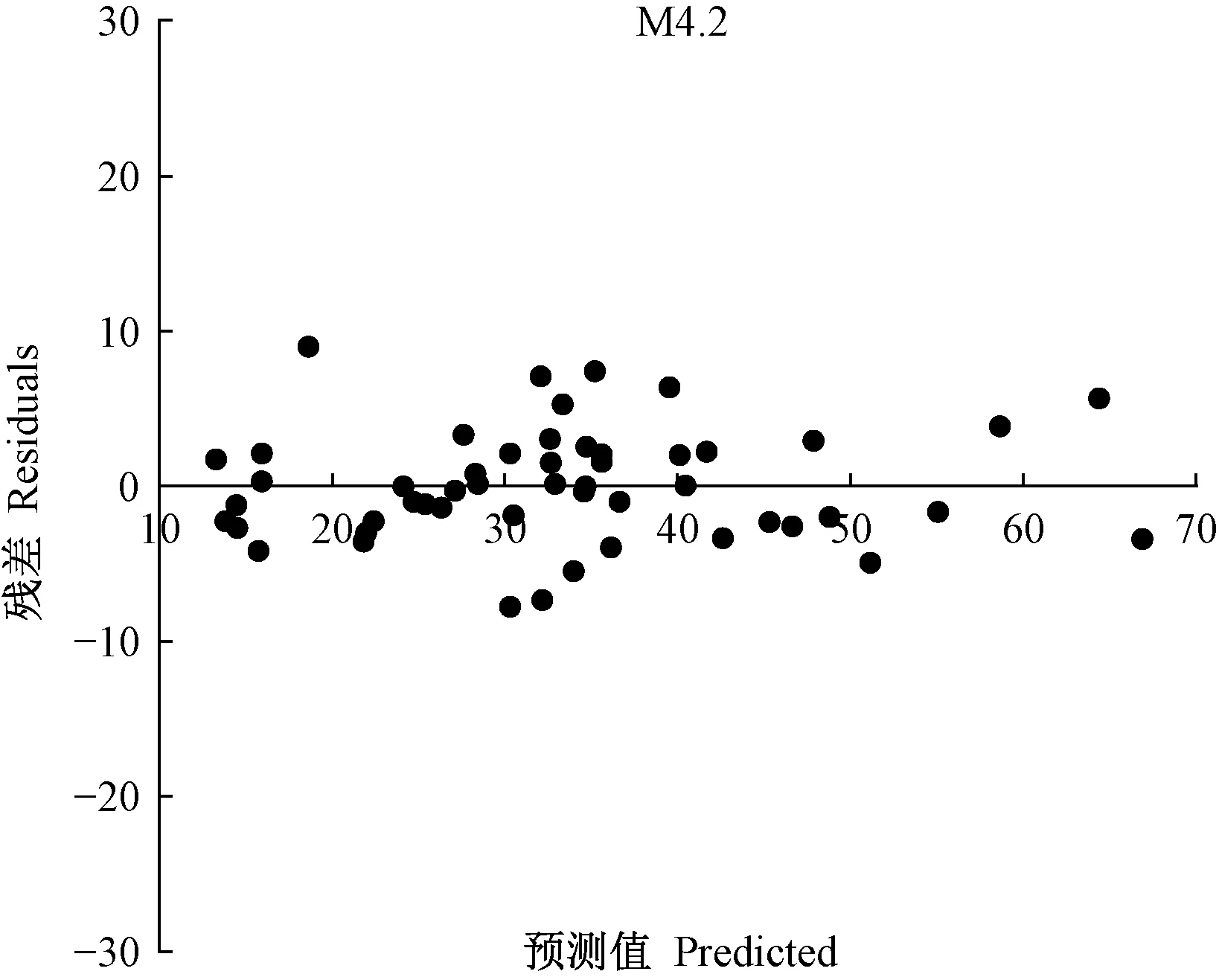
图2 混合效应模型M4.2残差分布

利用模型M4.2绘制基于立地类型组的胸径生长曲线簇，由图3可知，曲线拟合效果较好，进一步证实模型的精度和适用性。

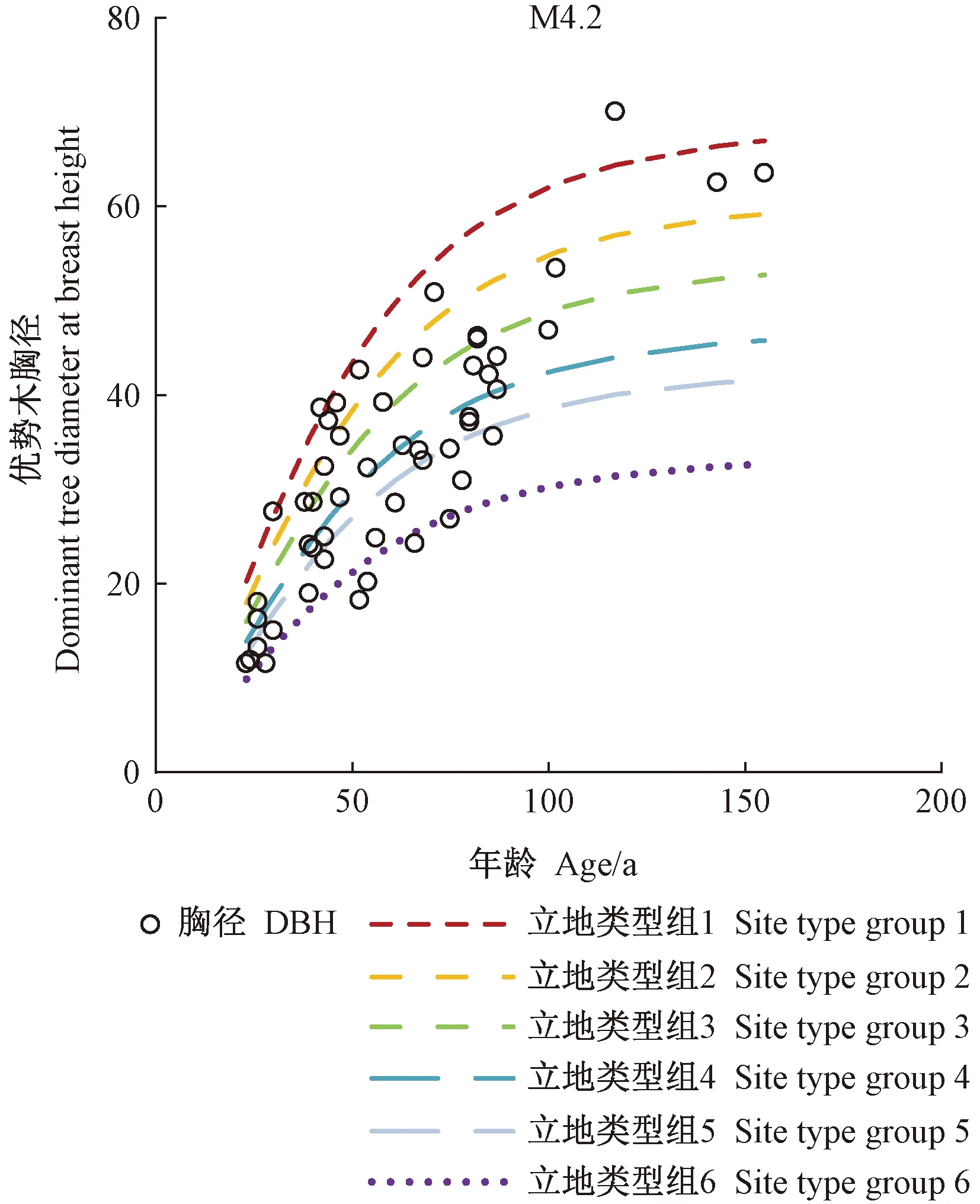
图3 基于立地类型组的胸径生长曲线簇

3.5 基于混合效应的立地质量评价模型

模型M4.2两边同时取对数：

lnDj=b×lnaj×[1-exp(-c×AGE)]，

(9)

得

(10)

因此，

SQEIM-DBH=aj×[1-exp(-c×AGE0)]^b+ε。

(11)

式中： SQEIM-DBH为基于最粗优势木胸径生长的立地质量评价指标；AGE0为基准年龄。

整理式(11)导出以最粗优势木胸径为指标的基于立地分级的立地质量评价模型为：

SQEIM-DBH=aj×[1-exp(-c×AGE0)]^

(12)

代入参数值得到最终模型为：

SQEIM-DBH=aj×[1-exp(-0.03×AGE0)]^

(13)

根据模型(13)，当给定基准年龄(AGE0)、优势木年龄(AGE)和胸径(D)时，在确定立地类型组下得到a参数值，即可得到立地质量评价指标SQEIM-DBH。

3.6 立地质量评价模型适用性检验

林分断面积是反映立地质量的常用指标，以林分每公顷断面积为因变量，林分密度指数、年龄、立地质量评价指标为自变量，采用方差分析验证立地质量评价模型的可行性，结果见表10。

表10 显著性检验

由表10可知，立地质量评价指标与林分断面积显著相关，以最粗优势木胸径为指标评价栎类天然林立地质量、预估林地生产力在理论上具有可行性。

4 讨论

立地质量是森林生产力的基础，对森林更新、树种选择、地力维持和经营管理至关重要。在异龄林或混交林中，林分密度不影响优势木的树高-胸径关系(李清顺等， 2021； Vanclayetal.， 1988； Huangetal.， 1993)，通常利用优势木树高-年龄(立地指数法)、树高-胸径(立地形法)评价立地质量，其中立地指数法应用最为广泛。但野外实地调查时，胸径测量相比树高更准确，且本研究通过相关分析也得到林分最粗优势木胸径生长与株数密度无显著相关性，而与立地因子显著相关，因此可以根据优势木胸径生长评价林地立地状况。本研究表明，影响湖南栎类天然林优势木胸径生长的因子包括海拔、坡度、坡位和坡向，其中海拔的影响最显著，坡度、坡位、坡向的影响次之。海拔主要影响气温，坡位、坡度主要影响土壤水分和养分再分配，坡向主要影响光照条件，再结合降雨、气温等气象条件，不同立地条件下的树木生长会存在差异(邓秀秀等， 2016； 高若楠等， 2019)。

混合效应模型广泛用于林分生长建模中，不仅可以提高模型精度，还能够提升模型适用性。齐战涛等(2021)基于混合效应模型构建含气候效应的杉木断面积模型，为森林经营者在气候影响下采取合理的经营措施提供了理论参考。本研究构建含立地类型的湖南栎类天然林最粗优势木胸径生长模型，通过分析随机效应参数发现， 立地类型影响最粗优势木胸径生长最大值。由残差分布可知，将初始立地类型作为随机效应加入模型构建混合效应模型的残差分布明显更加集中、均匀，说明混合效应模型精度更优，能够更好拟合湖南栎类天然林最粗优势木胸径生长。不同立地类型对优势木生长的影响差异可通过立地类型混合效应参数值体现出来。为简化立地类型数量，应用k-means聚类将影响效果相近或相同的初始立地类型聚类成6个立地类型组，并作为随机效应加入最优基础模型构建非线性混合效应模型，R2为0.9269，相比基础模型提高26.7%，相比含初始立地类型的混合模型提高2.8%，说明含立地类型组的非线性混合效应模型能够更加精确拟合湖南栎类天然林最粗优势木胸径生长状况。6个立地类型组对应6组参数值，根据不同参数值a可得到不同立地类型组下优势木胸径生长状况，就本研究结果来看，立地类型组1的最粗优势木胸径生长最佳，立地类型组6的最粗优势木胸径生长最差，因此，基于立地类型的湖南栎类天然林最粗优势木胸径生长模型可为经营者在不同立地条件下的经营管理提供参考。

5 结论