Timoshenko自由梁迭代法计算木材弹性模量和剪切模量的适用性*
王 正 周宇昊 沈肇雨 何宇航
(南京林业大学材料科学与工程学院 南京 210037)
弹性模量、剪切模量和泊松比是表征材料的弹性常数,亦是材料的3项基本物理特性参数。木材是正交各向异性材料,提高其弹性常数测试精度尤为重要(谭守侠等,2007; 董浩然等, 2022; 阮锡根等, 2005; 刘鸿文,1983)。木材弹性常数测试方法可分为静态法和动态法两大类,近年来,利用动态振动法测试木材和木质复合材料弹性常数研究取得了显著成果(Chuietal., 1990; Chui,1991; Rossetal., 1994; 马功勋,1996; 王正等, 2006; 2013; 2014; 王正,2007; 周海宾等, 2007a; 2007b; Wangetal., 2012; 2016a; 2018; 2019a; 胡英成,2001; 胡英成等, 2001; Turketal., 2008)。Timoshenko自由梁迭代法是一种具有代表性的动态测试材料弹性模量和剪切模量的方法,该方法以Timoshenko梁理论(Timoshenko, 1965)为基础,即梁横向振动时考虑梁的剪力和回转效应对其弯曲频率的影响。Timoshenko自由梁迭代法测试木材弹性模量和剪切模量时,首先测试自由梁的第一阶和第二阶弯曲频率,然后应用迭代程序计算木材的弹性模量和剪切模量(Chuietal., 1990; Chui,1991; 周海宾等, 2007a),但对该方法的适用范围研究尚少,且其测试精度受试件不同长厚比的影响较大。
鉴于此,本研究基于试验探究Timoshenko自由梁迭代法测试木材和木质复合材料弹性模量和剪切模量的适用性,重点考虑材料弹性模量和剪切模量的测试精度,寻求梁试件合适的长宽比。
1 方法
1.1 Timoshenko自由梁迭代法
自由状态下,Timoshenko梁的第一阶弯曲频率(f1)和第二阶弯曲频率(f2)提供了包含弹性模量(E)和剪切模量(G)2个非线性方程式:
f1(E,G)=0,f2(E,G)=0。
(1)
2个非线性方程式构成1个非线性方程组,该方程组可用编程的迭代方法求解。计算程序输入参数为梁长度(m)和厚度(mm)、梁材料密度(kg·m-3)、矩形截面因子(k)、第一阶弯曲频率(Hz)、第二阶弯曲频率(Hz),输出参数为弹性模量E(MPa)和剪切模量G(MPa)。若迭代收敛,可同时计算出正常的E和G; 否则不能计算出正常的E和G或根本计算不出E和G,即迭代发散。
1.2 Euler自由梁法
Euler自由梁的一阶弯曲频率(f1b)与弹性模量(E)的关系为:
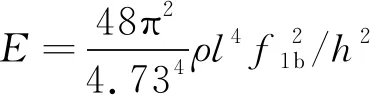
(2)
式中:E为弹性模量(Pa);l为自由梁长度(m);h为自由梁厚度(m);f1b为自由梁一阶弯曲频率(Hz);ρ为气干密度(kg·m-3)。
1.3 自由板扭转振型法
自由板一阶扭转频率(f1t)与剪切模量(G)的关系为:
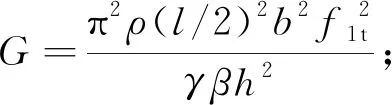
(3)
式中:G为剪切模量(Pa);l为自由板长度(m);b为自由板宽度(m);h为自由板厚度(m);γ为自由板振型系数;f1t为自由板一阶扭转频率(Hz);ρ为气干密度(kg·m-3)。
1.4 自由杆件扭转振动法
自由杆件一阶扭转频率(f1t)与剪切模量(G)的关系为:
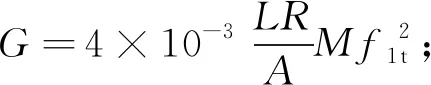
(4)
式中:G为剪切模量(MPa);L为杆长(mm);b为杆矩形截面宽度(mm);a为杆矩形截面厚度(mm);A为杆矩形截面面积(mm2);M为杆件质量(kg);f1t为一阶扭转频率(Hz)。
2 试验
2.1 试验材料
山毛榉(Fagussylvatica),含水率13%; 云杉-松-冷杉(spruce,pine and fir,SPF),含水率11.5%; 单板层积材(laminated venner lumber,LVL),含水率9%; 西加云杉(Piceasitchenrsis),含水率9.5%。
2.2 试件制作
制作山毛榉、SPF等树种的径、弦向梁试件,西加云杉横纹梁试件和LVL整板下料的纵、横向梁试件,以及相应的板试件,试件总数共49块。梁试件和板试件的基本参数分别见表1、2。
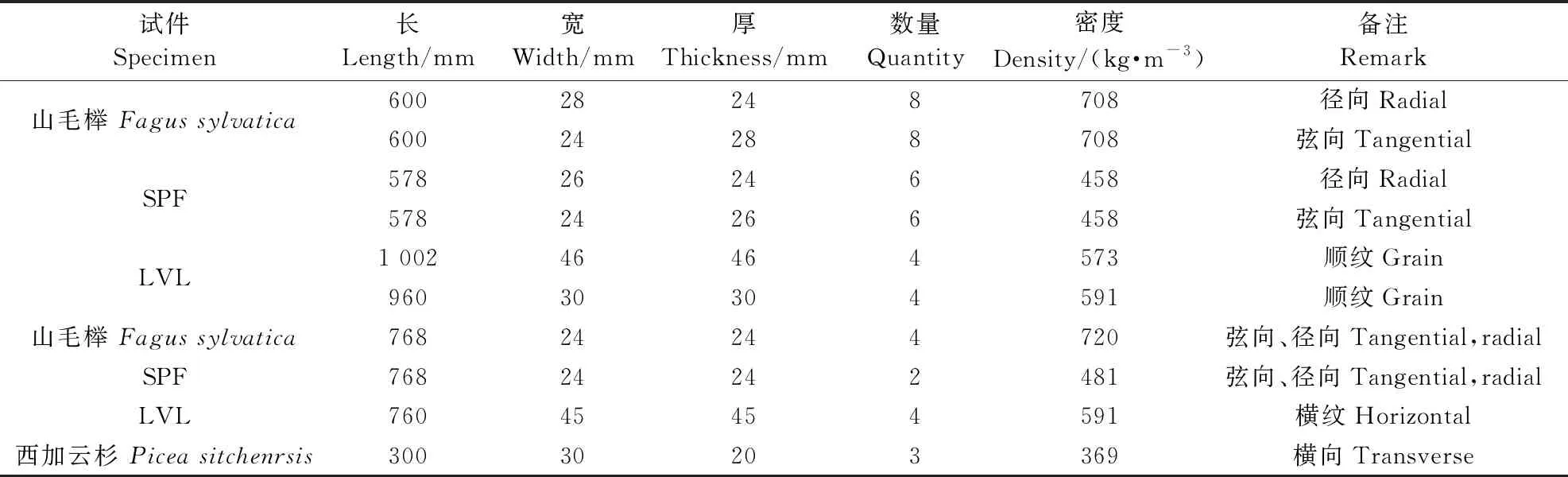
表1 梁试件基本参数

表2 板试件基本参数
梁试件和板试件用刚性系数小于0.4 N·m-1的弹性绳自由悬挂,实现两端自由约束的自由梁和自由板(图1、2)。
2.3 试验仪器及其配套件
CRAS振动及动态信号采集分析系统1套,包括调理箱、采集箱、信号与系统分析软件; CA-YD-125型压电式加速度计1只,1.5 g; HK-30型木材含水率测试仪1只; TG328B型电光分析天平1台,0.001 g; 游标卡尺1把,0~150mm; 橡胶锤1把; 尼龙锤1把; 钢尺1把,0~1 m。
2.4 试验设计
2.4.1 测试工况(梁试件) 记录每根梁试件长宽面和长厚面上的木纹特征,即弦向或径向。每根梁试件测试梁弯曲振动沿试件厚度和宽度方向2种工况,从一种工况到另一种工况只需将试件绕其纵轴线转动 90°,垂向激励即可实现; 每根径向和弦向迭代程序中输入的h指与梁弯曲振动方向相对应的梁横截面尺寸(宽或高)。
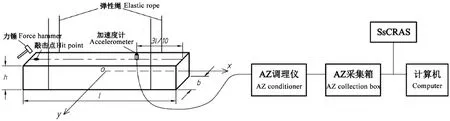
图1 自由梁测试系统
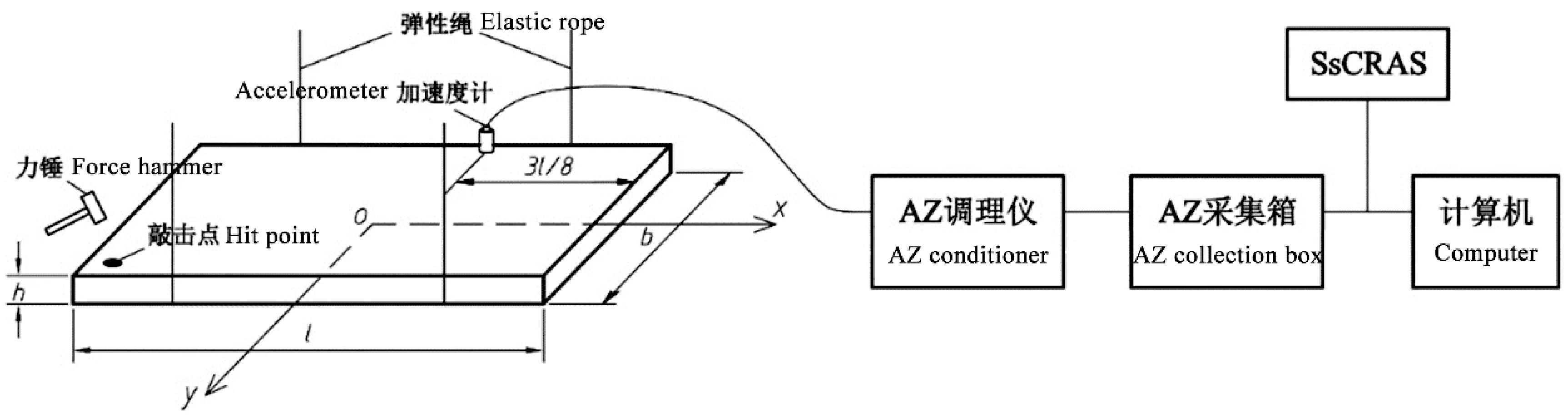
图2 自由板测试系统
2.4.2 截短试验 正方形截面的梁试件依次按l/h=32、28、24、20、16、14、12、10、8截短,截面宽厚不相等的梁试件按实际梁长截短,测试不同长厚比试件的第一阶和第二阶弯曲频率,应用迭代程序计算其弹性模量和剪切模量,以寻求弹性模量和剪切模量依赖于梁试件长厚比的变化规律,并确定能迭代出正确弹性模量和剪切模量的试件长厚比下限值。在迭代计算时,着重探讨矩形截面因子k取值对迭代结果的影响。按常规k应取0.833,但从能量观点看k也可取0.913(邵蓓珠等, 1988),本研究分别以k=0.833和0.913作为迭代程序输入,计算不同长厚比试件的弹性模量和剪切模量,以寻求合宜的k取值。
对于板试件,依次按l/b=6、5、4.5、4、3.5、3截短,测试自由板一阶弯曲频率和一阶扭转频率,根据自由板扭转振型法和自由杆件扭转振动法(Wangetal., 2016b; 2019b; 程可等, 2015)一阶扭转频率测试值计算其剪切模量,由Euler自由梁法一阶弯曲频率测试值计算其弹性模量,以此验证自由梁迭代法计算木材弹性模量和剪切模量的有效性。
2.5 频率测量
敲击试件激发自由振动,安装于试件上的加速度计接收振动信号,经放大、滤波、A/D转换为便于计算机处理的数字信号,通过采集器采集和信号分析软件(或专用的频谱分析仪)测得试件频谱,从频谱图上读取频率(Timoshenko, 1965)。
测试梁试件和板试件频谱时,加速度计安装位置和敲击点位置不同(图 1、2)。对于梁试件,当长厚比变小时,要适时提高其分析频率范围; 对于板试件,加速度计安装于沿板长边距角点3l/8处,敲击板对角线上另一个角点; 为识别弯曲频率和扭转频率,要敲击板面中心点。
同一根梁试件2种测试工况,编号为山-3的试件长576mm,矩形截面长边为24.61mm(弦向木纹特征),短边为24.37mm(径向木纹特征),振动方向沿短边和长边的频谱分别如图3、4所示。
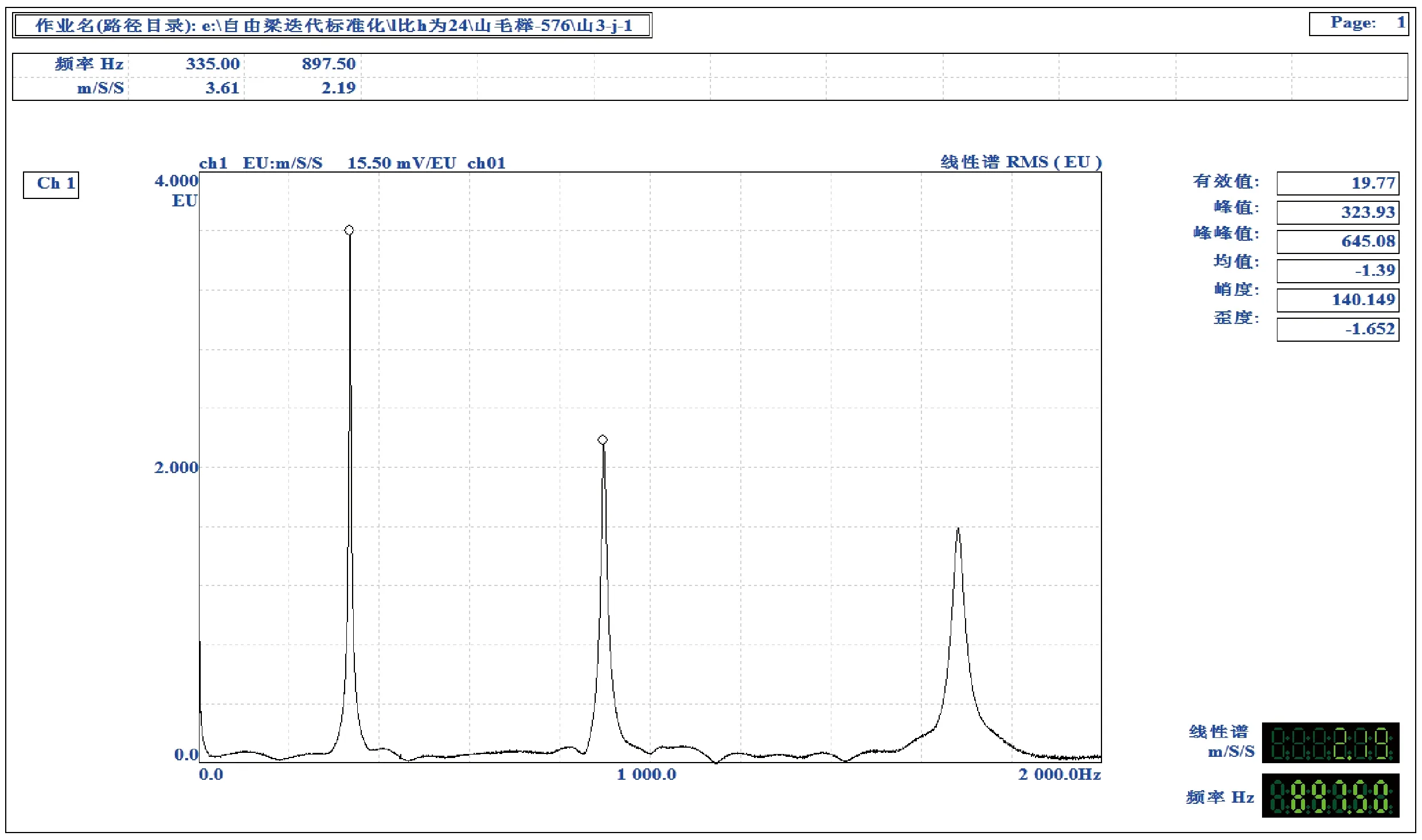
图3 山毛榉 576mm×24.61mm×24.37mm梁试件径向频谱
3 结果与分析
3.1 自由梁迭代法计算的弹性模量和剪切模量
山毛榉径向和弦向、SPF径向和弦向以及LVL垂直和平行胶层激励的梁试件,在不同长厚比l/h下采用自由梁迭代法计算的弹性模量和剪切模量如图5~10所示(矩形截面因子k取0.833)。
图4 山毛榉 576mm×24.37mm×24.61mm梁试件弦向频谱
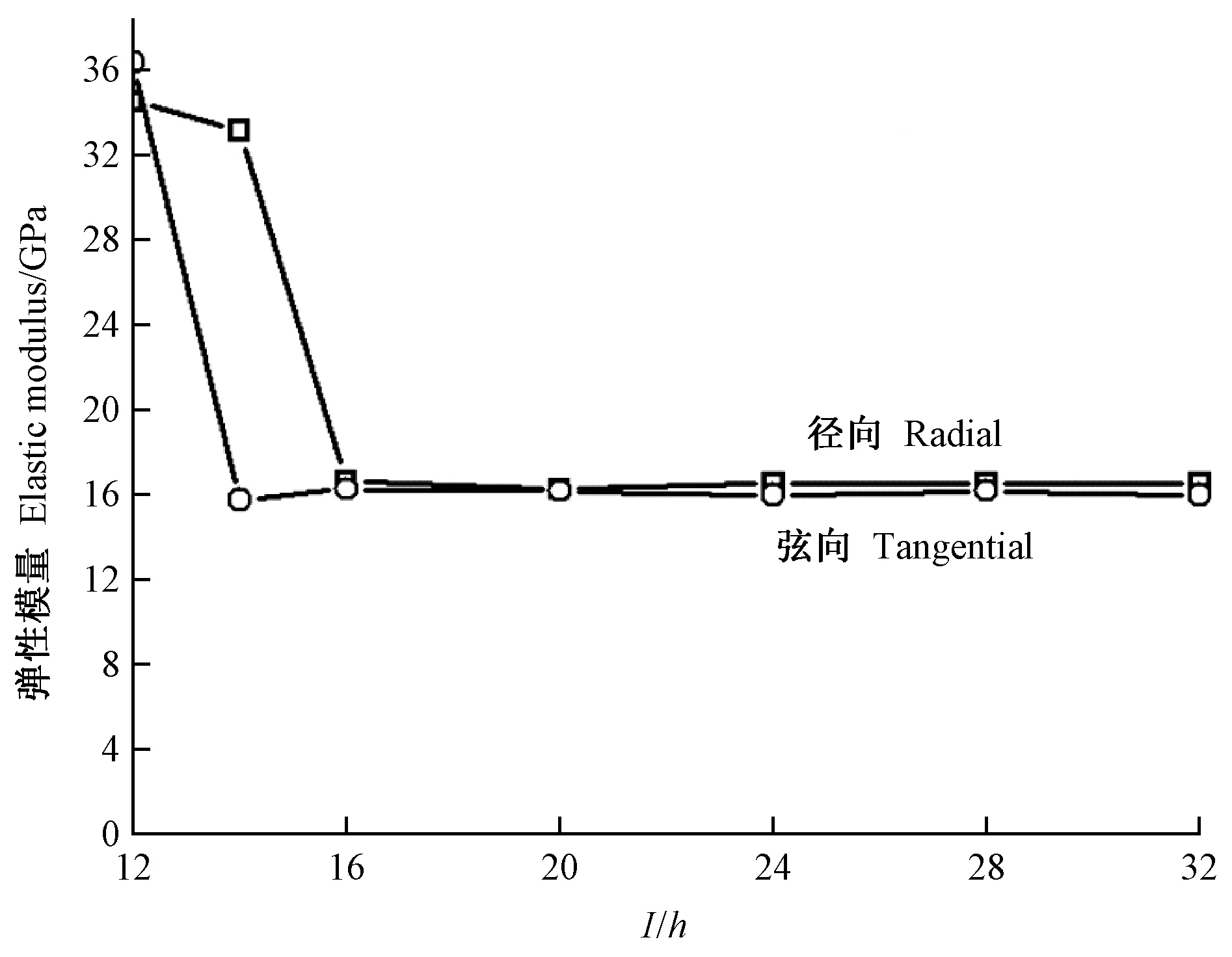
图5 山毛榉弹性模量(E)计算值随梁长厚比(l/h)的变化
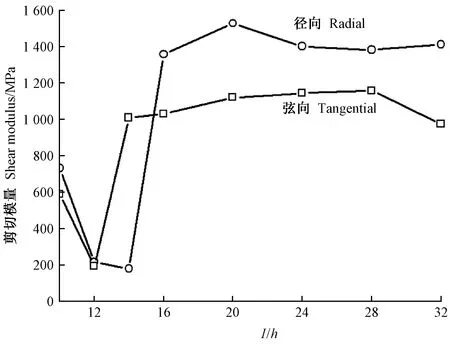
图6 山毛榉剪切模量(G)计算值随梁长厚比(l/h)的变化
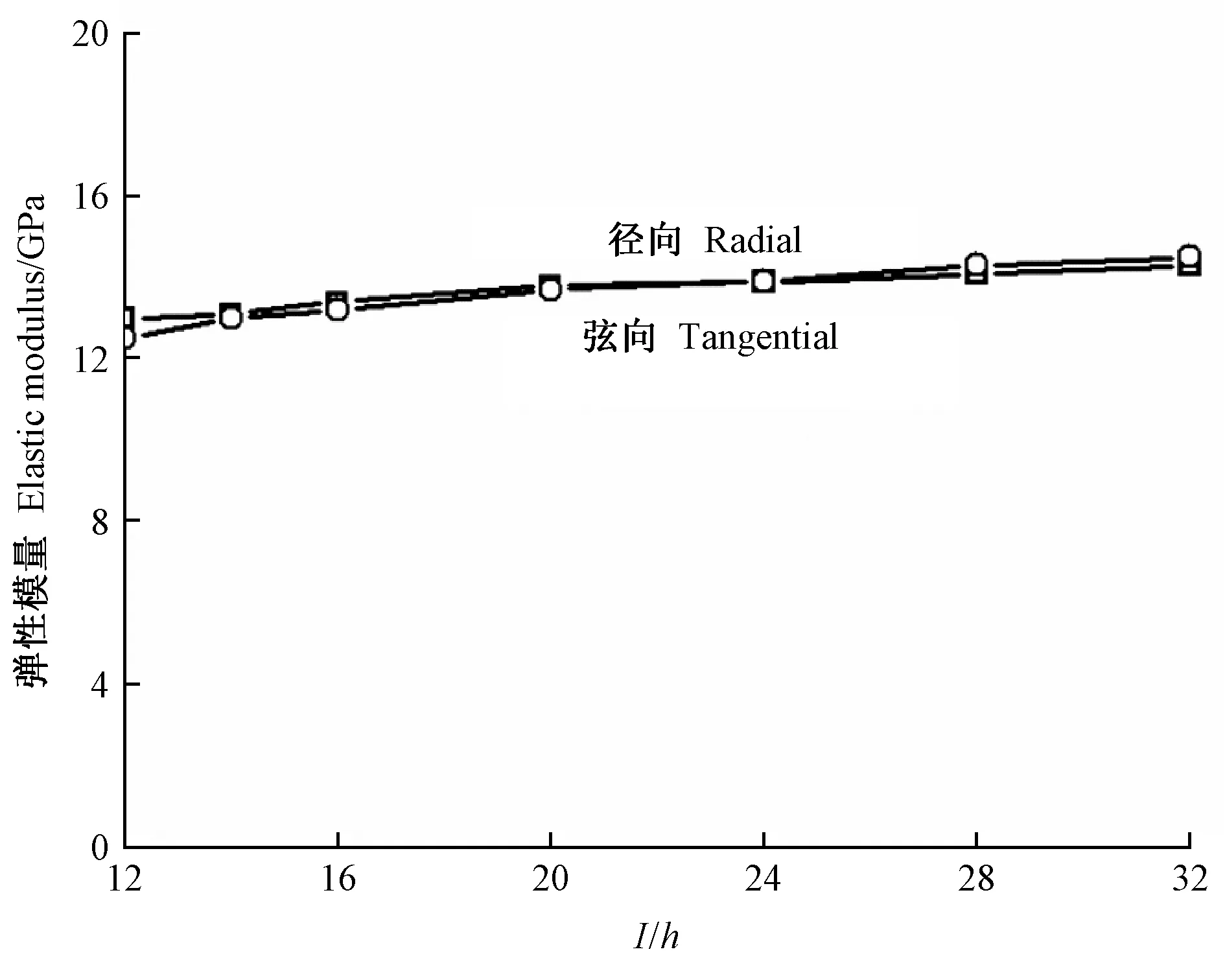
图7 SPF弹性模量(E)计算值随梁长厚比(l/h)的变化
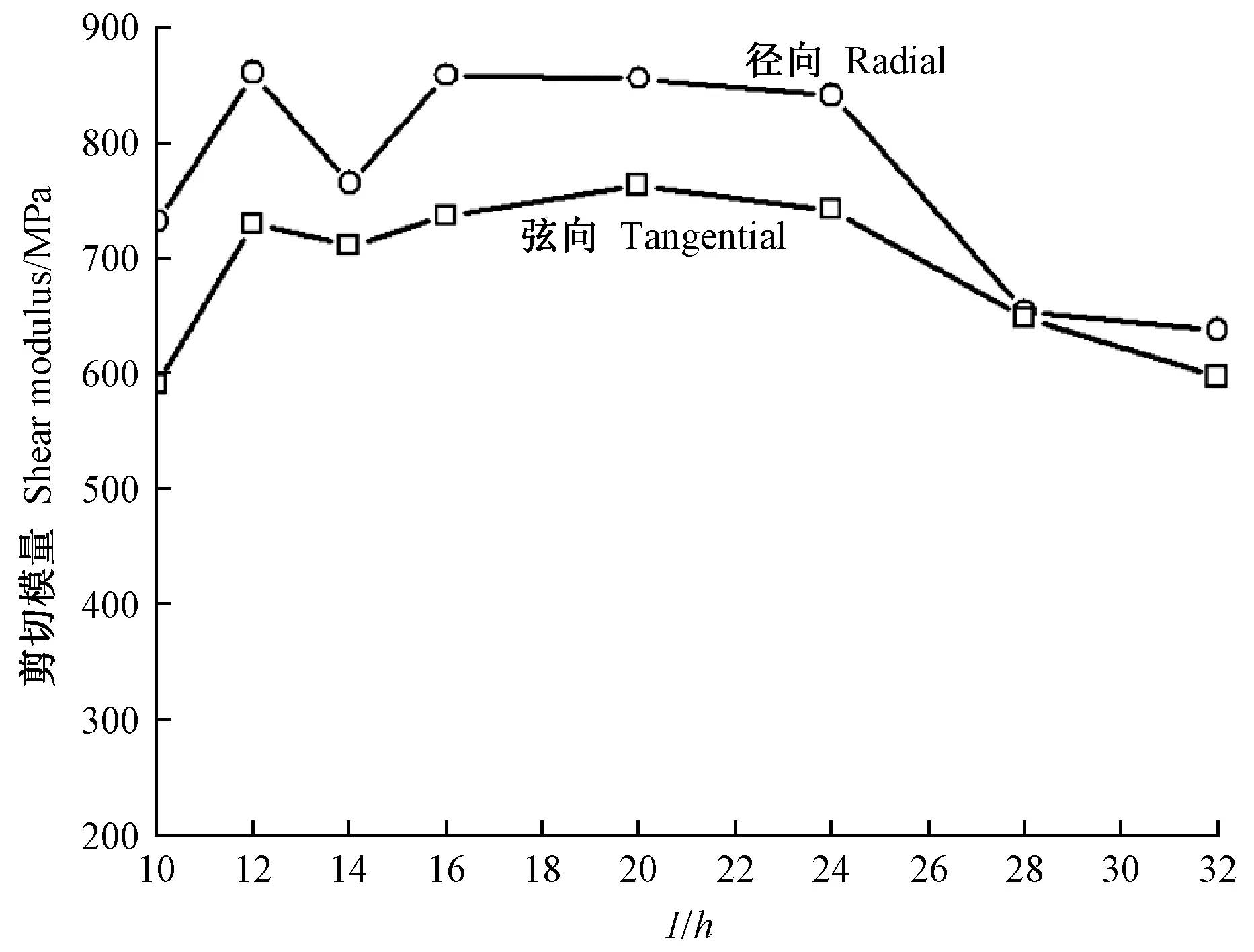
图8 SPF剪切模量(G)计算值随梁长厚比(l/h)的变化
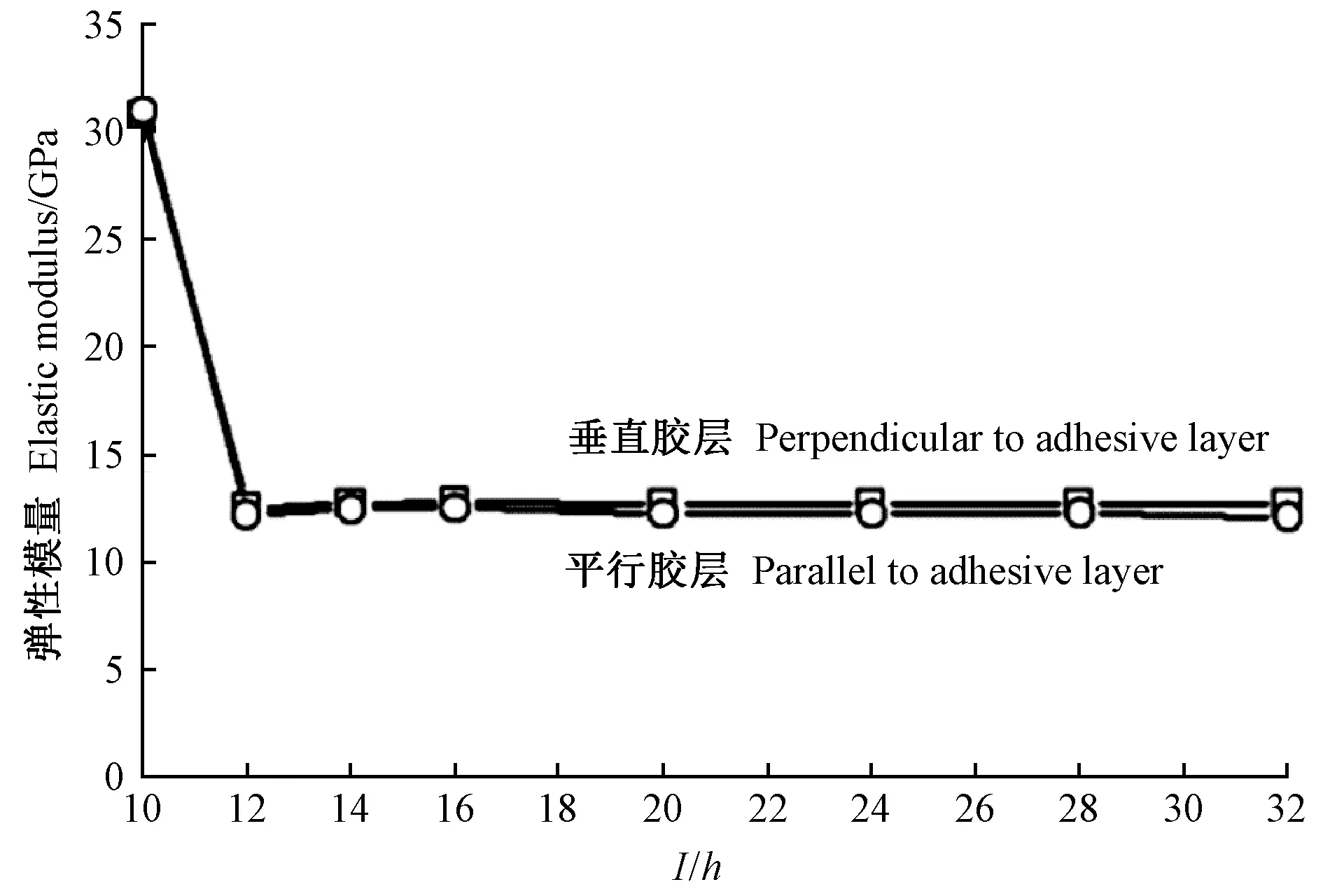
图9 LVL弹性模量(E)计算值随梁长厚比(l/h)的变化
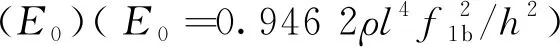
表4为山毛榉径向和弦向、SPF径向和弦向以及LVL顺纹(垂直平行胶层激励)试件在不同长厚比下采用Timoshenko自由梁迭代法计算的弹性模量和剪切模量均值。
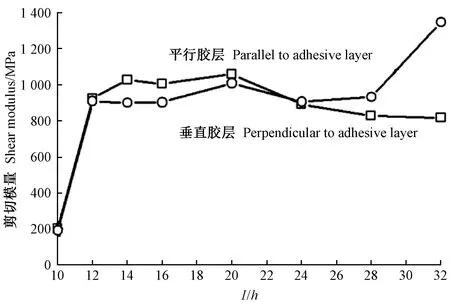
图10 LVL剪切模量(G)计算值随梁长厚比(l/h)的变化

表3 SPF、山毛榉和LVL采用自由梁迭代法计算的E/E0随梁长厚比(l/h)的变化
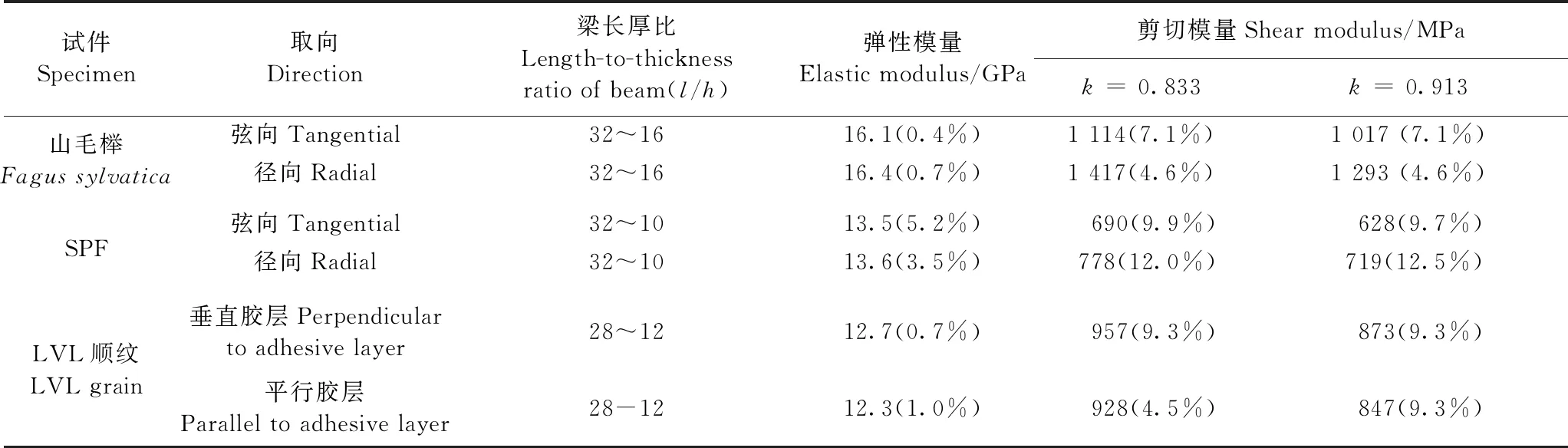
表4 山毛榉、SPF和LVL采用自由梁迭代法计算的弹性模量和剪切模量①
分析上述结果可知: 1)采用自由梁迭代法,当迭代计算出正常的弹性模量和剪切模量时,径向和弦向弹性模量几乎相等,且不随梁长厚比变化; 木材径向和弦向剪切模量虽随梁长厚比变化较大(表4、图6和图8),但根据其平均值可以区分开来。 2)自由梁迭代法存在一个与树种有关的试件长厚比下限值,当试件长厚比小于该下限值时,虽能测得自由梁的第一阶和第二阶弯曲频率,但不能计算出正常的弹性模量和剪切模量,迭代计算出的弹性模量相对正常值成倍增大,剪切模量成倍减小,或根本计算不出弹性模量和剪切模量。 3)当迭代计算出正常的弹性模量和剪切模量时,矩形截面因子k取0.833计算出的剪切模量比k取0.913大9.6%,弹性模量几乎相等(表4)。 4)对于SPF、山毛榉和LVL,当梁长厚比l/h=20~24时,Timoshenko自由梁迭代法计算的弹性模量(E)与Euler自由梁法计算的弹性模量(E0)的相对误差在7%以内(表3),l/h=20~24长厚比试件采用自由梁迭代法计算的弹性模量和剪切模量基本处于l/h=32、28、24、20、16相应的弹性模量和剪切模量计算值均值(图5~10)。因此,采用自由梁迭代法计算弹性模量和剪切模量时,推荐使用长厚比l/h=20~24的梁试件。
3.2 自由杆件扭转振动法和自由板扭转振型法测试的剪切模量
在板不同长宽比(l/b)条件下,采用自由杆件扭转振动法和自由板扭转振型法测试的山毛榉、SPF剪切模量如图11、12所示。
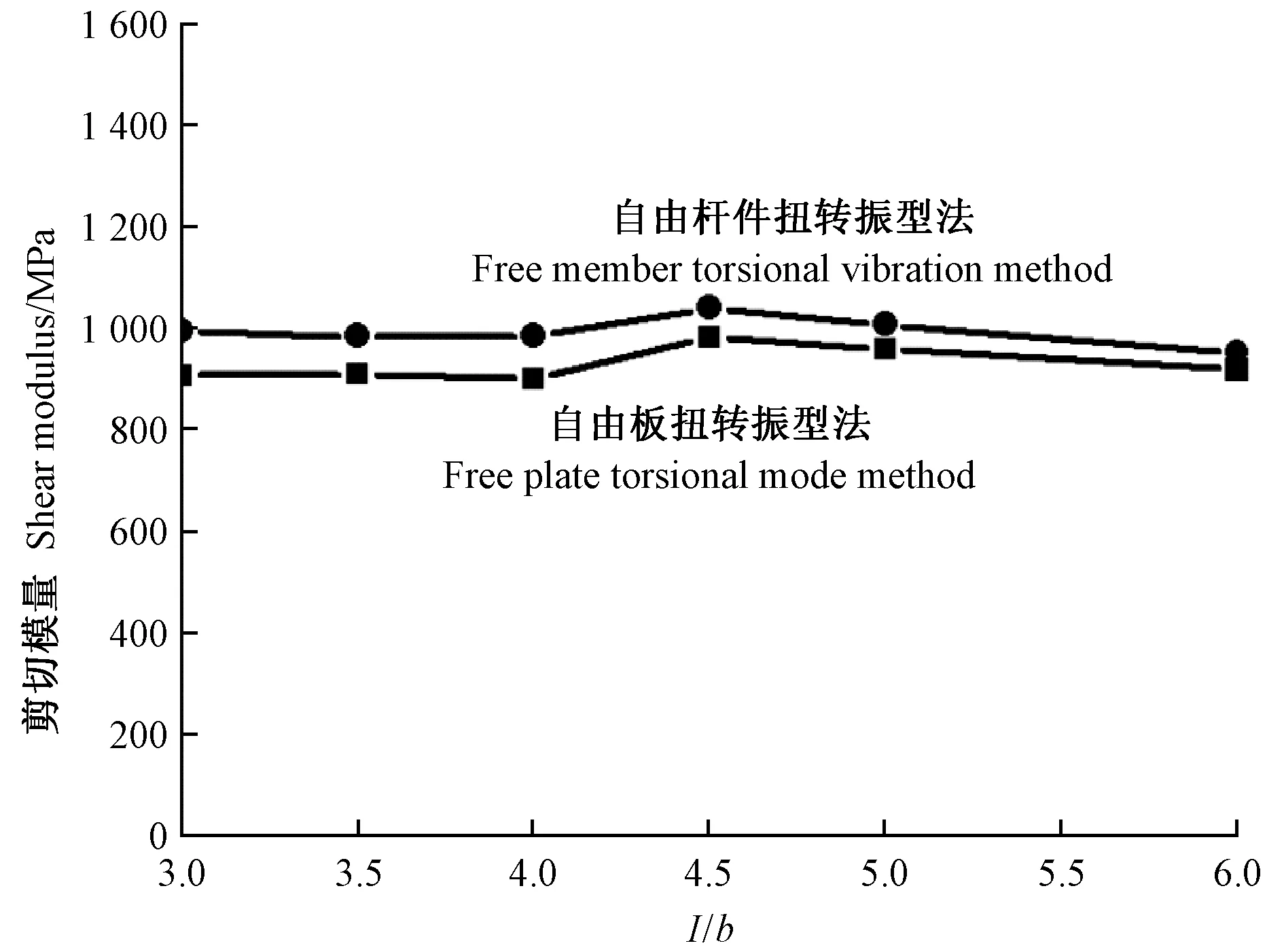
图11 自由板扭转振型法和自由杆件扭转振动法测试的山毛榉剪切模量随板长宽比(l/b)的变化
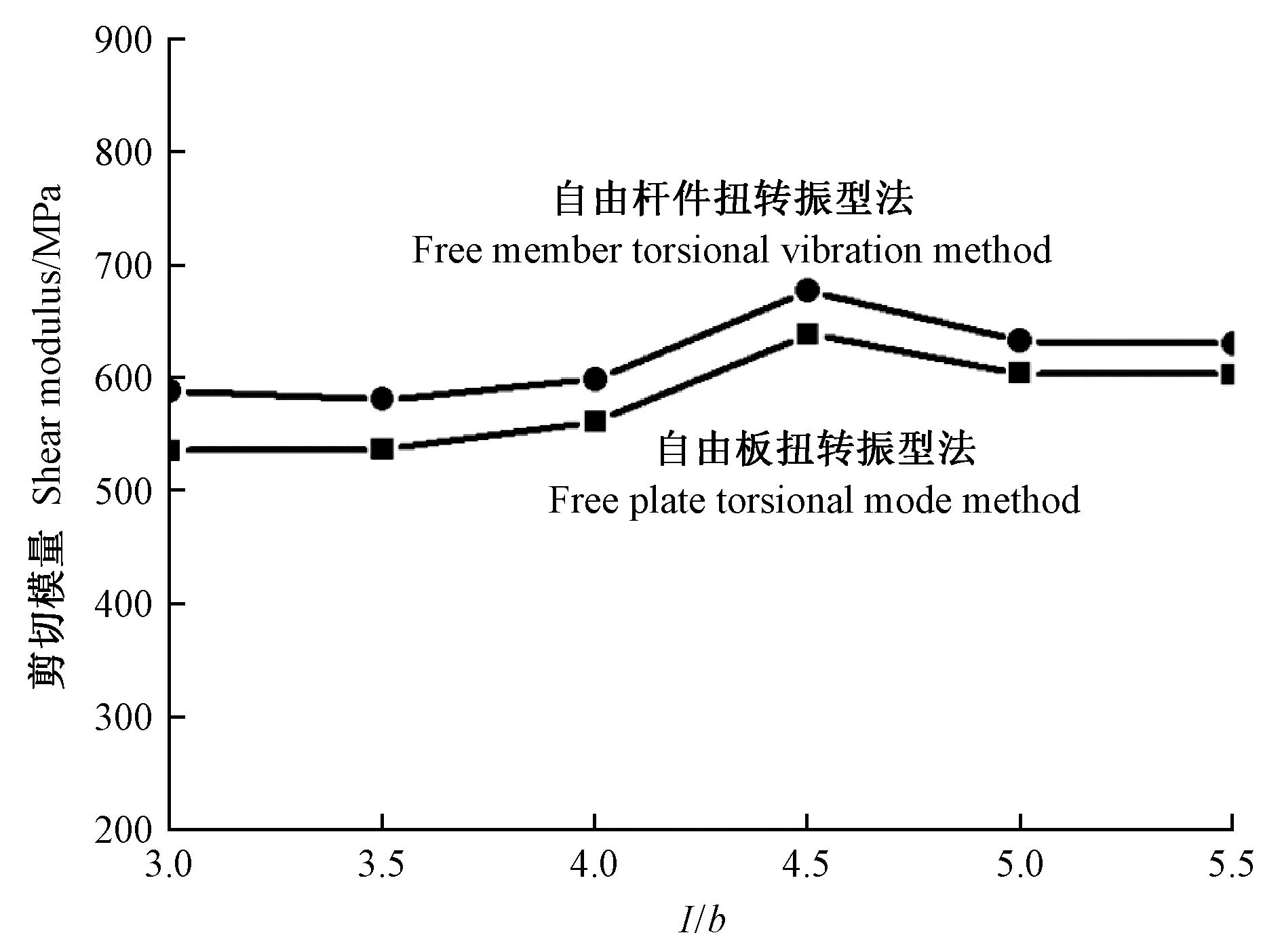
图12 自由板扭转振型法和自由杆件扭转振动法测试的SPF剪切模量随板长宽比(l/b)的变化

表5 自由杆件扭转振动法和自由板扭转振型法测试的山毛榉、SPF和LVL剪切模量
在板不同长宽比条件下,采用自由杆件扭转振动法和自由板扭转振型法测试的山毛榉、SPF和LVL剪切模量如表5所示。
分析上述结果可知,在板不同长宽比条件下,自由杆件扭转振动法测试的剪切模量均比自由板扭转振型法大7%左右。与自由板扭转振型法和自由杆件扭转振动法测试的剪切模量相比,自由梁迭代法计算出的剪切模量偏高,其偏高程度与矩形截面因子k取值有关。对于山毛榉弦向、SPF弦向、LVL顺纹(垂直于胶层激励),当k=0.833和0.913时,自由梁迭代法计算出的剪切模量比自由杆件扭转振动法分别高12.2%和2.3%,比自由板扭转振型法分别高19.9%和9.3%(表4、5)。基于自由梁第一阶和第二阶弯曲频率应用迭代程序计算木材和木质复合材料弹性模量和剪切模量发现,k取0.833时计算不出正常的弹性模量和剪切模量,但k取0.913时却可以计算出正常的弹性模量和剪切模量(表6),这说明矩形截面因子取0.913相对于0.833而言,不仅扩大了试件l/h的适用范围,即降低试件l/h下限值,还能够改善自由梁迭代法对剪切模量的高估。试验发现,西加云杉横纹梁可以测出其第一阶、第二阶弯曲频率,但采用自由梁迭代法却计算不出弹性模量和剪切模量; 若采用自由板扭转振型法测试西加云杉横纹板(404mm×70mm×12mm,9块),则可得出其弹性模量为349 MPa,剪切模量为40 MPa。从LVL整板垂直其纵向下料的横向梁(760mm×30mm×30mm,3根)可以测出其第一阶、第二阶弯曲频率,但采用自由梁迭代法也计算不出弹性模量和剪切模量; 若采用自由板扭转振型法测试LVL横向木纹板(760mm×240mm×30mm),则可得出其弹性模量为721 MPa,剪切模量为694 MPa。
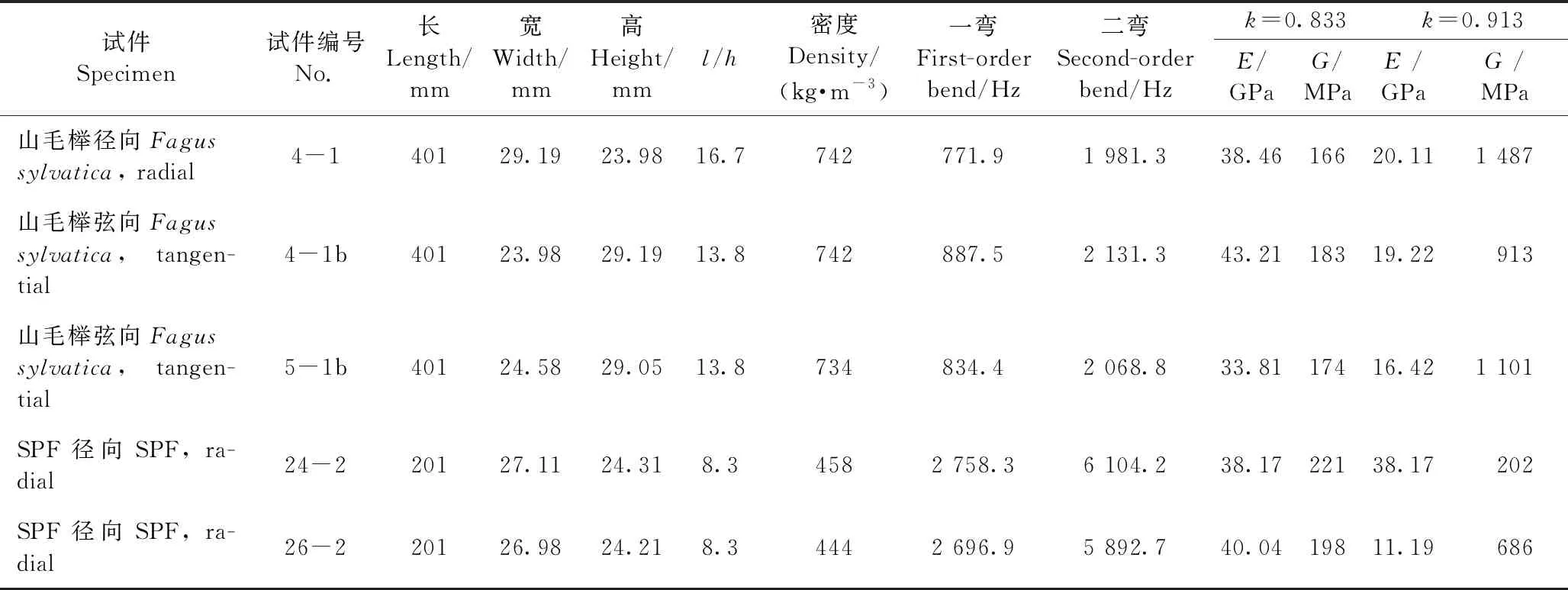
表6 矩形截面因子k取值对自由梁迭代法计算结果的影响
综上可知,若一次试验同时测试出高精度的弹性模量和剪切模量,Timoshenko自由梁迭代法不是最佳选择。自由板扭转振型法和自由杆件扭转振动法测试的是自由板频谱,从频谱图上读出板试件的一阶弯曲频率和一阶扭转频率,将一阶弯曲频率测试值代入式(2)得到弹性模量,将一阶扭转频率测试值代入式(3)或式(4)得到剪切模量,2种方法测试的剪切模量随板长宽比变化平稳,自由板扭转振型法或自由杆件扭转振动法测试的剪切模量精度高于自由梁迭代法。
4 结论
1) 存在一个与树种有关的试件长厚比下限值,当试件长厚比小于该下限值时,自由梁迭代法不能计算出正常的弹性模量和剪切模量或根本计算不出弹性模量和剪切模量。
2) 对于径向和弦向梁,自由梁迭代法计算出的弹性模量几乎相等,且不随梁长厚比变化; 木材径向和弦向剪切模量虽随梁长厚比变化较大,但根据其平均值可以区分开来。
3) 自由梁迭代法计算出的剪切模量与矩形截面因子k取值有关,当k取0.833和0.913时,分别高于自由杆件扭转振动法(自由板扭转振型法)剪切模量测试值12.2%和2.3%(19.9%和9.3%)
4) 为保证自由梁迭代法测试精度,推荐采用长厚比20~24的梁试件动态测试其第一阶和第二阶弯曲频率,并用矩形截面因子取0.913进行迭代计算木材的弹性模量和剪切模量。

