地下矿山主溜井支护钢板冲击模拟与影响规律
杨继海 王忠慧 张令非 王 雄
(中国矿业大学(北京)力学与建筑工程学院,北京 100083)
0 引言
主溜井是金属矿山重要的地下结构,井下开采的矿石都在此临时集储和转运[1], 按照矿石在溜井中的运动方式不同,溜井可以分为上部溜矿段和下部储矿段,溜矿段溜井主要承受矿石的冲击作用。由于溜井身处地下百米,地形地质、工程环境复杂,长期受到冲击荷载及摩擦作用,以及远处的爆破可能带来的影响[2],溜井井壁会逐渐的破损、扩大,最终发生垮塌事故[3],如国内的程潮铁矿[4-5]、新城金矿[6]、国外的南非Kloof金矿[7]等。对井壁围岩进行加固的锰钢板随着冲击次数的增多,也会逐渐发生脱落现象,因此研究溜井井壁受到矿石的冲击力大小规律,对于研究溜井井壁破坏规律有着重要的意义。
目前,针对溜井井壁的破损,大量学者取得了一系列的研究成果。宋卫东[8]对程潮铁矿溜井进行了相似比试验,并与理论推导进行对比,得到井壁处的破坏程度和破坏区域较为一致。路增祥[9]通过能量与变形的关系,得到了垂直溜井中井壁受到了冲击和剪切两种形式的破坏。马驰[10]对溜井中矿石的运动状态和影响因素进行了理论分析。叶海旺[11]利用PFC2D数值软件建立了溜井系统的模型,以冲量为指标,分析了溜井井壁的冲击损伤特征。
利用Abaqus数值模拟软件中的显式动力学模块,结合某矿山主溜井采用的钢板支护案例,以冲击力大小为指标,分析不同卸矿工况下的支护钢板的冲击力影响规律。
1 工程概况
此矿山为露天转地下开采的金属矿山,矿山采用主井、副井、斜坡道开拓,主溜井担负矿山露天转地下开采后主要矿石的转载、临储任务,主溜井通过矿石量1亿t以上,是矿山的主要工程之一。主溜井深228 m,采用全长支护,主溜井上部标高-321 m,下部标高-549 m,其中,-321~-331 m段为锰钢衬板支护,井筒直径4.5 m。在溜矿段,锰钢衬板支护时常受到矿石的冲击作用,自2017年投入生产以来,先后多次发生棚堵、支护混凝土及锰钢板脱落等现象。
2 模型及参数设置
卸矿后的矿石运动轨迹及运动速度等可通过散体运动学理论求解,由于矿石形状的差异,矿石之间的相互作用,致使矿石真实的运动轨迹较为复杂,文中不考虑矿石流的作用,即不考虑矿石之间的相互作用,仅考虑单块矿石对井壁支护结构的影响。
2.1 有限元模型的建立
通过对矿山主溜井的调查,收集相关的地质资料和监测资料,选择矿石与溜井井壁支护结构的碰撞位置处作为研究对象。该区域常年受铁矿石的冲击,井壁采用锰钢板加固,锰钢板厚80 mm,取锰钢板宽2 m。通过现场的数据得知,铁矿石直径大小主要集中在0.2~0.4 m,矿车卸下的矿石简化为球体,由于文中不对矿石进行分析,所以球体设置为刚性,参考点位于球心位置处。取钢板处适当大小的圆作为接触区域,矿石与锰钢板的接触设置为钢球表面与锰钢板上的圆的面面接触,采用动力接触方法和有限滑动公式。锰钢板约束形式为四周固定。
考虑到单矿石与钢板发生碰撞前的运动轨迹可由运动方程求解,同时为减少数值模拟计算时间,只计算矿石与钢板发生的碰撞时刻,结构形式与尺寸(钢板宽2 m,小球直径0.3 m)如图1所示。

图1 模型图
2.2 参数选取
通过现场调查和资料收集,根据矿山所做的各种岩石力学试验获得岩石力学指标,相关计算参数的采用值见表1。

表1 材料属性
2.3 模型的合理性验证
通过Chau[12]的研究,滚石在冲击过程中的自转动能仅为平动动能的10%左右,所以滚石的自转在碰撞过程中起到的作用较小,因此忽略矿石的自转作用。
以矿石直径D为0.3 m,矿石冲击角度为90°,矿石冲击速度为10 m/s为例,图2为系统的能量图,包括系统内能、系统动能及系统总能量随碰撞过程的变化图。
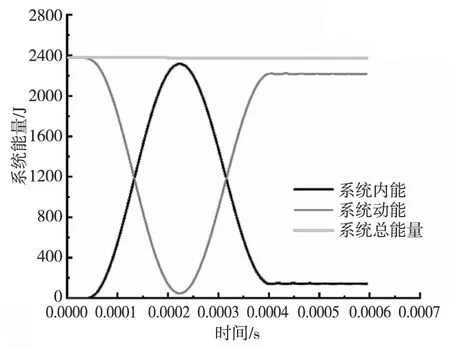
图2 系统能量历程曲线图
系统总能量来自矿石的速度,即冲击能量均由矿石动能转化,总能量大小为
由图2可见,系统总能量在碰撞前后基本保持不变,最大能量为2 375 J,最小能量为2 373 J,能量损失率低于0.09%,满足能量守恒定律。在整个碰撞及回弹过程中总能量保持不变,发生碰撞时系统内能先增大后减小最后保持稳定状态,保持稳定阶段时的内能大于0,说明经碰撞后系统存在一定内能,此能量使系统产生一定的应变能。而系统的动能由最大逐渐减小接近于0,发生回弹时会逐渐增大并趋于稳定。系统内能在2.25e-4 s时达到最大,最大为2 316.36 J,同时动能降为最小,最小为45.95J。其他工况同样满足如上的趋势,总体上系统能量的变化趋势符合相关理论,因此计算结果合理。
3 计算结果与分析
3.1 典型工况下支护钢板应力分析
鉴于模型的计算具有重复性,选取2.3节的典型工况进行应力分析。
图3所示为矿石冲击支护钢板不同时刻的应力云图,可知,矿石与锰钢板发生碰撞后,首先在碰撞中心处产生应力,随着碰撞的进行,应力开始向四周扩散。在碰撞过程中,锰钢板的最大Mises应力呈现先增大后减小的趋势,由下文可知,与矿石冲击力总体趋势相同,冲击力在0.2 ms达到最大,此时支护钢板的Mises应力也达到最大,钢板最大Mises应力为148 MPa,远低于钢板的屈服强度,矿石在0.4 ms左右发生回弹,在矿石回弹之后,支护钢板内的应力会继续向四周扩散。
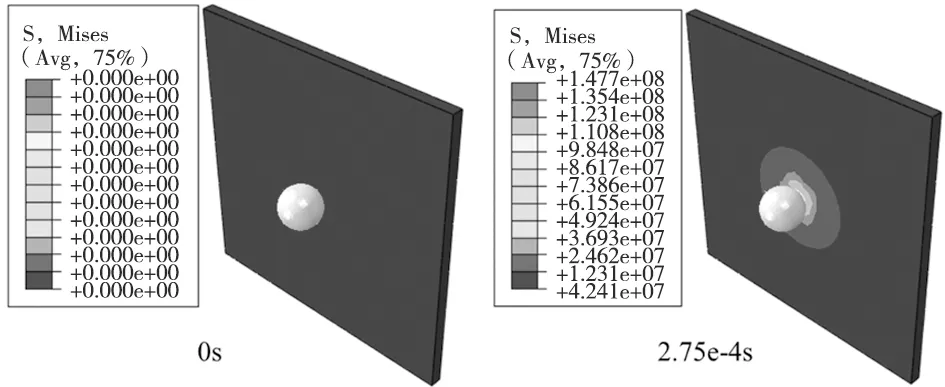
图3 数值计算结果
3.2 矿石冲击速度的影响规律
为研究矿石冲击速度对支护钢板产生的影响,选取矿石直径D为0.3 m,冲击角度为90°,冲击速度V分别为5、10、15、20、25 m/s的方案。图4为矿石不同冲击速度冲击锰钢板产生的冲击力时程曲线及峰值力变化曲线。
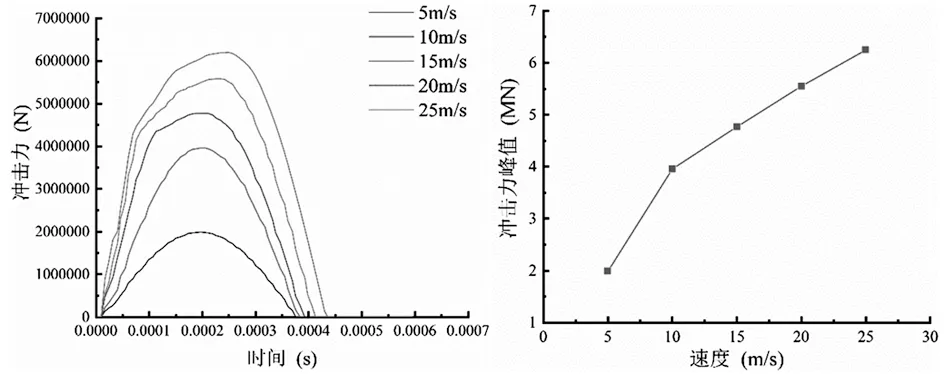
图4 不同冲击速度下冲击力时程曲线及峰值力变化曲线
由图4可见,随着碰撞过程的发生,矿石对钢板的冲击力由0先增大后减小,最后趋于0并稳定,不同速度下冲击力峰值约在0.2~0.25 ms处达到。在0.35~0.45 ms时矿石与锰钢板发生了分离,冲击力减小为0。随着速度的增大,冲击力峰值和矿石与锰钢板分离都有延后的趋势。相同矿石质量,相同入射角度,不同冲击速度对锰钢板产生的冲击力峰值大小不等,由图4可见,随着矿石冲击速度的增大,对锰钢板产生的冲击力也越大。在矿石冲击速度分别为5、10、15、20、25 m/s时,峰值冲击力分别为1.99、3.96、4.77、5.58、6.40 MN。在速度大于5 m/s后,峰值冲击力与矿石的速度呈正比关系。
3.3 矿石质量的影响规律
为研究矿石质量对支护钢板产生的影响,由于矿石直径与矿石质量存在确定的函数关系,为建模方便,以矿石直径代表矿石质量,选取矿石速度V为10 m/s,冲击角度为90°,矿石直径D分别为0.2、0.25、0.3、0.35、0.4 m,其质量分别为14.24、27.82、48.07、76.33、113.94 kg。图5所示为矿石不同质量,即不同矿石直径冲击锰钢板产生的冲击力时程曲线及峰值力变化曲线。
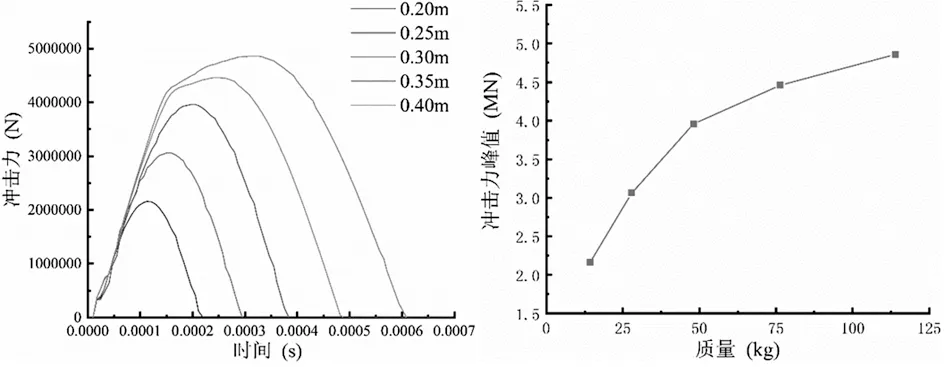
图5 矿石不同直径下冲击力时程曲线及峰值力变化曲线
由图5所示,不同直径矿石对支护钢板的冲击力大小同样都满足先增大后减小的趋势。矿石速度相同,相同入射角度,不同直径矿石对支护钢板产生的冲击力大小不等,随着矿石质量的增大,对钢板产生的冲击力也越大。在矿石质量分别为14.24、27.82、48.07、76.33、113.94 kg,最大冲击力分别为2.16、3.06、3.96、4.46、4.86 MN。由图5可见,与速度对冲击力产生的影响不同的是,随着矿石质量的增加,矿石与钢板发生碰撞的时间明显增加,在矿石质量分别为14.24、27.82、48.07、76.33、113.94 kg时,碰撞持续时间分别为2.11e-4、2.86e-4、3.75e-4、4.82e-4、6.03e-4 s。随着矿石质量的增加,峰值冲击力的增加速度有减缓的趋势,这是由于矿石的质量是通过直径表示的,这样就导致不同直径矿石冲击过程中接触面积有所不同。在矿石直径增大到一定程度后,峰值冲击力的变化越来越小。
3.4 冲击角度的影响规律
为研究矿石冲击角度对支护钢板产生的影响,选取矿石直径D为0.3 m,冲击速度V为10 m/s,冲击角度分别为90°、60°、45°、30°、0°。由于矿石与支护钢板的冲击存在一定夹角,所以分别考虑法向冲击力和切向冲击力。
由图6、图7可知,在矿石质量相等,相同速度情况下,即矿石直径D=0.3 m,矿石速度V=10 m/s,法向峰值冲击力随冲击角度的减小而减小,而切向峰值冲击力随冲击角度的减小而增大。在冲击角度分别为90°、60°、45°、30°时,法向冲击力峰值分别为3.96、3.32、2.64、1.78 MN,切向冲击力峰值分别为0.107、0.158、0.199、0.236 MN,在冲击角度为0°时,法向冲击接近于0。由图7可见,不同冲击角度下法向冲击力要远远大于切向冲击力,相比于法向冲击力而言,随着冲击角度的减小,切向冲击力所占的比例越来越大,法向冲击损伤会逐渐减小,而切向剪切损伤逐渐增大。而且随着冲击角度的减小,法向冲击力峰值减小速度与切向冲击力峰值的增加速度也有增大的趋势。
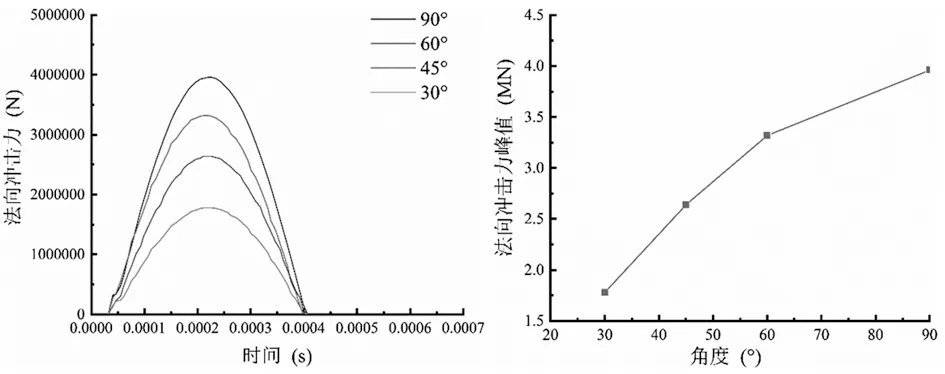
图6 不同冲击角度下法向和切向冲击力时程曲线及峰值力变化曲线
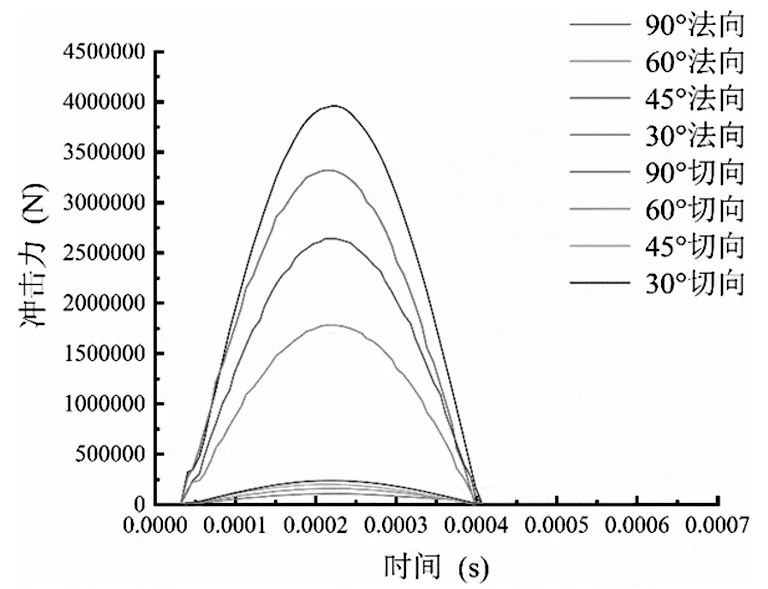
图7 不同冲击角度下冲击力时程曲线
4 结语
1)典型工况下,矿石冲击力与支护钢板的Mises应力都满足先增大后减小的趋势,且同时在0.2 ms左右达到最大,矿石在0.4 ms左右发生回弹,矿石回弹后,应力继续向外扩散。
2)在矿石冲击钢板的过程中,冲击力随矿石速度的增大而增大,速度达到5 m/s之后,峰值冲击力与矿石的速度成正比,且随着速度增大,峰值冲击力与冲击时间有延后的趋势;冲击力随着矿石质量的增大而增大,峰值冲击力的增加速度有减缓的趋势,冲击时间明显增加。
3)对矿石斜向冲击钢板,应考虑法向作用和切向作用时,法向冲击力随冲击角度的减小而减小,而切向冲击力随冲击角度的减小而增大,随着冲击角度的减小,切向冲击力所占比例越来越大,法向峰值冲击力的减小和切向冲击力的增大都有增大的趋势。

