基于仿真分析的墙壁插座面板厚度对其单边卡扣脱扣的影响分析
王也,陈旭波,常嘉能,姚思捷
(宁波公牛电器有限公司,浙江 慈溪 315314)
0 引言
墙壁插座因其安装结构设计在其装饰部件以下,墙上拆装需要先拆卸其装饰部件。墙壁插座面板是墙壁插座的必要装饰部件之一,因此墙壁插座面板的拆卸是用户使用该产品的必须环节。在拆卸面板过程中,面板卡扣脱扣时的脱扣力及其脱扣行程都是影响面板能否拆卸的重要指标;而面板的厚度直接影响面板脱扣时的脱扣力与脱扣行程[1]。
墙壁插座面板常被设计成单边中间带撬口,两侧内置隐藏卡扣的结构[2]。在具体设计中,面板两侧的内置卡扣常因墙壁插座的不同功能需求设计的不同结构而让位,导致卡扣布局不对称;或者因其他功能部件使面板侧边产生缺口而导致面板撬口两侧刚度不同,导致卡扣脱扣受力不对称等,使在撬动撬口时,两侧卡扣难以同时脱扣而形成一边卡扣脱开、另一边卡扣仍扣紧的情况[3]。在该情况下,仍扣紧的卡扣的再脱扣会形成单边卡扣脱扣的工况。在该工况下,因力矩平衡的破坏,面板在撬动过程中存在侧边翻转,单边卡扣脱扣受力与脱扣行程发生变化。而脱扣行程受使用工具的局限往往存在操作阈值,因此探究单边卡扣脱扣受面板厚度的影响规律有一定的意义。本文使用仿真分析的方法,基于一种墙壁插座实际结构模型,进行面板厚度对其单边卡扣脱扣的影响分析,探究其影响规律及其局限,并与试验测试结果对照验证其可靠性。
1 结构模型与工况
本次分析的结构模型如图1所示,脱扣相关结构包含面板和固定架。模型结构采用中间撬口、两侧隐藏式卡扣的设计。其中,右侧卡扣因避让其他功能性结构不与左侧卡扣相对于中间撬口对称,左侧卡扣中心距撬口中心19.65 mm,右侧卡扣中心距撬口中心32 mm;且面板于撬口右侧侧边存在缺口。该模型为原始尺寸模型。
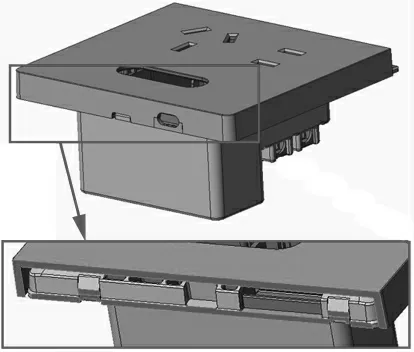
图1 参与分析的墙壁插座结构模型
常规脱扣过程起始于使用工具对中间撬口的向上抬动,抬动过程中面板整体发生中间高、两侧低的翘曲形变和撬口侧边向外侧翻转的形变,面板卡扣与固定架卡扣由中间向两侧滑动,卡扣滑动结束后完成脱扣。其中,在卡扣相同的情况下,面板形变的程度直接决定卡扣滑动的速度;而其形变程度由面板的刚度及撬口至卡扣的力矩决定。
显而易见,因面板侧边缺口的影响,该结构面板左侧刚度大于右侧,且在撬动撬口脱扣过程中,左侧卡扣力矩小于右侧。当左侧卡扣完成滑动后,右侧卡扣未完成,故而存在右侧卡扣需单边脱扣的工况。
本文分析的单边脱扣工况与常规脱扣工况类似,其显著差别为:在脱扣过程中,没有图1所示左侧卡扣的作用。
2 力学模型
依据卡扣脱扣的实际工况,基于本文分析的结构模型建立卡扣在脱开过程中力学模型,如图2所示。撬动撬口后面板开始向上运动时,在卡扣处面板卡扣与固定架卡扣的区域,固定架卡扣受到面板的力P,并认为力P集中于卡扣几何模型的几何中心A点,该力的力矩为点A到面板在A的几何尺寸对称点B的长度L1;面板撬动后绕撬口对称端翻转,则固定架在点A的几何尺寸对称点B受到相反的力,其力矩对应为L2。而在点A处,面板卡扣受到固定架阻碍其向上运动的反作用力F,该力在坐标系上的分量分别为Fx与Fy。依据Herz接触理论[4],两物体接触局部均会形成垂直于受力方向的局部形变并形成平面,在该模型中该平面在该平面坐标系的投影与X坐标轴的夹角为α。单个卡扣脱扣过程中B点受力力学表达式为
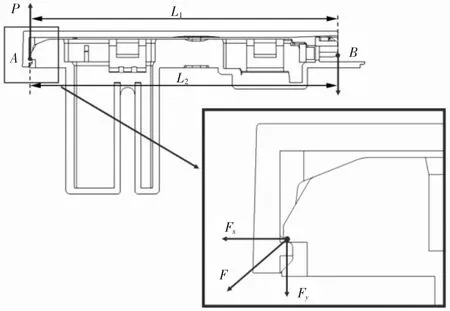
图2 卡扣力学模型

脱扣力是使结构变形克服固有结构阻碍的力,其大小与施加方无关。由该模型可以很明确地看出,脱扣力P的大小主要与Fy的大小相关,它们在脱扣过程的每个固定时刻保持力矩平衡。由式(2)可知,Fy与Fx关于α角相关,α角是由脱扣过程中力F的方向决定的,而该力的方向与面板的整体形变相关。可知,K是影响脱扣力的关键因素,该因素决定面板的形变,具体表现在它影响面板侧边翻折所需力的大小、面板顶面形变所需力的大小、面板卡扣与固定架卡扣接触形变形成的面在坐标系中的投影与X轴的夹角。
因为面板变形后可恢复为原形,刚度K为弹性形变范畴的弯曲刚度,则刚度K的表达式[5]为
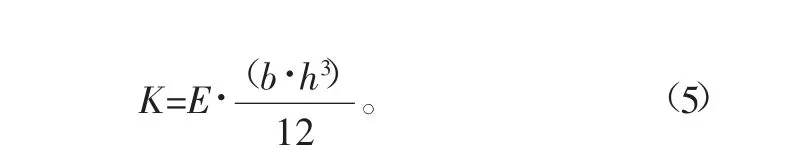
式中:E为弹性模量;b为截面宽度;h为截面高度。
依据式(5),截面高度(即弯曲方向的厚度)是影响面板刚度的高敏感因素,因此面板的厚度是影响脱扣的关键因素。这里面板的厚度分为面板侧边的厚度与面板顶面的厚度,面板侧边的厚度在实际设计中会影响墙壁插座的外沿尺寸,而外沿尺寸是固定值,因此本文主要讨论面板顶面厚度对脱扣的影响。
3 前处理
3.1 网格的划分
本文使用仿真试验的方法进行理论研究,而网格的密度直接关乎仿真结果计算的精度,但过高的网格数量却会增加仿真计算的计算量,延长计算时长并给设备带来负担。为平衡这一矛盾,采取整体网格密度较小、关键接触位置网格密度较大的原则划分网格。网格设置如表1[6]所示。
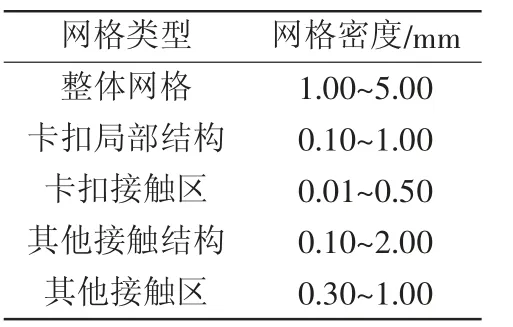
表1 网格设置参数
网格类型主要分为六面体网格和四面体网格,其中六面体网格的精度高于四面体网格,这是由有限元仿真计算方法所决定的,而四面体网格更适应复杂结构网格的划分;本文选择带中间节点的四面体网格,在保证网格划分效率的基础上使网格划分质量与六面体网格接近[7]。最终划分网格节点数为367 390,划分网格单元数为205 095。
3.2 约束与接触的设置
在实际拆卸环境下,墙壁插座各零部件之间及其固定架与墙壁之间包含螺钉连接等固定结构连接。在仿真环境下,这些连接采用约束连接线、连接面各自对应自由度或固定连接的方式进行模拟连接。
仿真设置的各零部件的接触面位置与实际安装各零部件卡扣及其他接触面的位置相同;在每对接触的选择上,选择面积较大的面为主接触面、面积较小的接触面为附属接触面。各个接触的接触形式及属性由实际测量获得,数据如表2所示。
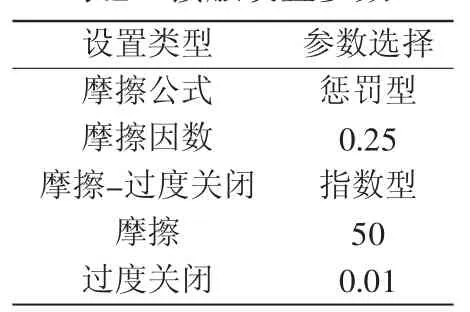
表2 接触设置参数
3.3 材料的选择
在实际工程生产过程中,为保证较高的生产效率,材料配比的精确性控制是一个区间而非某个固定值,这就导致不同批次材料的属性存在细微差异,为保证仿真分析的准确性,对被分析零部件实际使用的同一批次材料进行测量[8],并以此设置仿真材料参数,参数如表3所示。

表3 材料实测参数
3.4 载荷设置
卡扣作为基于零部件发生形变而扣锁的紧固结构,在扣合位置的结构尺寸一般采用过盈设计。在分析时,直接划分网格进行计算易造成网格穿透,并且穿透位置为卡扣扣合的接触面位置,这会导致接触面的交错,进而使接触失效,导致卡扣紧固脱开。因此需要对过盈扣合量进行临时载荷设置,使其在脱扣过程计算前脱离过盈状态,其中一个卡扣的临时约束设置如图3所示。设置位移载荷为临时载荷,在撬动载荷前生效,临时载荷作用在与卡扣垂直的面上,载荷方向与撬动载荷方向垂直,作用效果使设计过盈量消失且使接触面最短距离小于0.01 mm[9]。
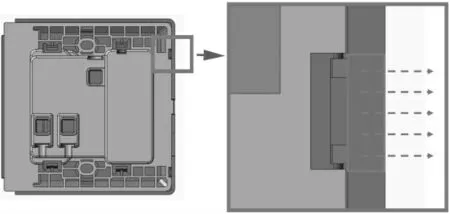
图3 临时约束设置示意图
由第2节可知,脱扣力是克服结构形变的反作用力,因此载荷设置为位移载荷,作用在撬口的几何中心上,且作用点以固定连接形式连接作用面。载荷作用方向垂直于作用面向上,为稳定计算且增加计算精度,载荷采用均匀施加的 方 法[10],单 步载荷设置为0.2 mm,载荷作用总长设置为7 mm。
4 脱扣力及脱扣状态的判定
将原始尺寸模型代入进行仿真计算,模拟实际单边脱扣工况,使模型左侧卡扣脱扣,并保持右侧卡扣扣锁,使撬口稳步向上运动,模拟右侧卡扣脱扣全过程。因在实际状态中,脱扣力的直观感受点位于撬口中,故而设定撬口中心的力为脱扣力点,脱扣全过程的脱扣力变化如图4所示。
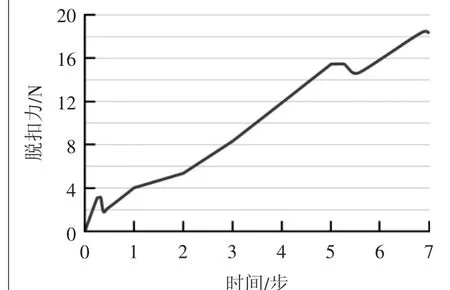
图4 原始尺寸模型单边脱扣力
在脱扣过程中,分析脱扣过程及脱扣力趋势可以看出:首先,面板与固定架整体发生弹性形变且卡扣并未开始脱扣,直至卡扣开始相对滑动,此时脱扣力开始提升,然后突降;然后,面板卡扣与固定架卡扣由面板中心向面板侧边方向发生相对滑动,同时二者形变加剧,脱扣力持续提升,直至卡扣局部开始发生塑性形变;最后,相对滑动结束,脱扣力持续提升,达到峰值后发生突降。脱扣力突降时模型整体及卡扣局部仿真应力云图如图5所示。
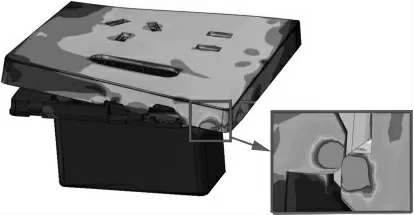
图5 原始尺寸模型脱扣状态应力分布
此时,面板左侧较高,面板中间及右侧发生大反转弹性形变,右侧卡扣右端上沿已滑过固定架卡扣右端下沿,脱扣区域中面板卡扣与固定架卡扣的局部应力高于材料屈服应力。此时卡扣完成相对滑动距离,卡扣扣位干涉完全脱开,卡扣接触区材料存在局部屈服。因此可以认为,脱扣力发生突降时,卡扣恰好完成脱扣。
5 面板厚度对脱扣的影响
由图5可见,单边卡扣脱扣时的脱扣行程(即撬口的位移)主要由面板的形变产生,而非脱扣的偏转产生。加厚面板的厚度可增加面板的整体刚度,使面板减小形变量,减少脱扣行程,因此设计不同面板厚度条件下的单边卡扣脱扣试验研究。
试验以原始尺寸模型为实验组,以面板分别加厚0.5、1.0、1.5、2.0 mm为对照组,在其他条件均相同的条件下进行仿真模拟试验,试验脱扣行程结果如图6 所示,脱扣力结果如图7所示。
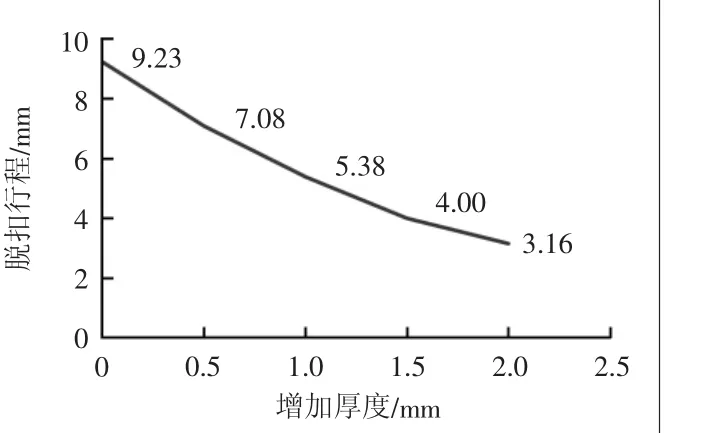
图6 不同厚度面板脱扣行程结果
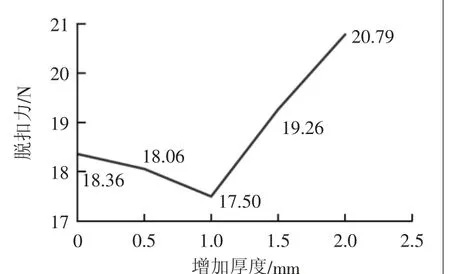
图7 不同厚度面板脱扣力结果
可见,随着面板厚度的提升,单边卡扣的脱扣行程始终呈下降趋势,但其下降折线的斜率也同时递减,厚度由0.5 mm增加至1 mm的斜率是厚度由0 mm增加0.5 mm的斜率的79.07%,而厚度由0.5 mm增加至1 mm的斜率仅达到其39.07%。可知,增加面板厚度是减少单边卡扣脱扣行程的可靠手段,但其效率随厚度的增加而递减。
通过分析脱扣力与面板厚度的关系可知,增加厚度在1 mm以下时,脱扣力随厚度增加而增加;增加厚度超过1 mm时,脱扣力随厚度增加而大幅度上升。这是因为卡扣脱扣过程是建立在一定程度的面板形变基础上的,由厚度增加导致的强度增加有利于力的传递,但过高的强度影响面板本身的形变,使脱扣力增加。
因在实际情况中脱扣行程越小就越容易操作,故而在本分析案例条件下,考虑到脱扣力的因素,增加面板厚度1.5 mm为最优,其脱扣力变化比例最小,仅为4.9%,而脱扣行程却可降低57%。
6 试验对标验证
脱扣行程是瞬间位移变化难以测量,故选择脱扣力为仿真试验对标指标。使用同一批次、相同仿真试验参数与条件相同的不同厚度的面板进行实际单边脱扣的脱扣力测量,其结果如图8所示。
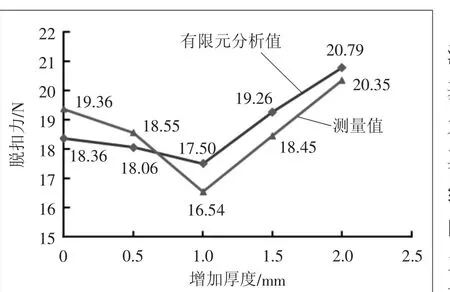
图8 不同面板厚度脱扣力测量值
以实际测量值为基准,有限元分析的仿真值在原始结构条件下的偏差值为-5.17%,在厚度增加0.5 mm时偏差值为-2.64%,在厚度增加1 mm时偏差值为5.79%,在厚度增加1.5 mm时偏差值为4.39%,在厚度增加2 mm时偏差值为2.16 %。可认为仿真脱扣力基本与实验值相当,仿真脱扣行程为实际脱扣行程。
7 结论
增加墙壁插座面板厚度可有效减少其单边卡扣脱扣行程,是减少其脱扣行程的有效方法,这是通过增加厚度以增加插座面板整体刚度来实现的。但脱扣行程的降低效率随厚度增加而衰减,且一味增加厚度会导致脱扣力持续增大;这是由于脱扣是基于面板形变发生的,过高的刚度会导致面板形变困难,达到同样的形变需要更大的力。因此,在考虑脱扣力框架下通过增加面板厚度而减少脱扣行程存在阈值。

