基于力学分析的汽车车灯卡扣结构优化设计

叶盾

(常州星宇车灯股份有限公司，江苏常州 213022)

0 引言

汽车灯具在设计生产过程中，会采用多种连接方式来实现不同部件之间的连接，如灯具的壳体与灯罩之间的胶合、焊接；反射镜与壳体之间的螺丝连接以及饰圈与其他部件之间的卡接。作为塑料件的组装方式，利用卡扣之间的卡接既方便又节省成本。卡扣卡接方式不仅在汽车车灯等塑料件上应用广泛，在众多其他领域[1]也得到有效应用。对于这种应用普遍的连接方式，很多主流汽车公司都在企业标准里详细给出了连接结构的卡接力和拉脱力的要求。如某汽车公司在对供应商的法规中明确规定卡合连接件结构的惯性锁峰值(最大卡接力)要小于70 N。江淮汽车的李书栓[2]利用有限元分析方法，研究了汽车门护板上卡扣的断裂强度和位移变形；法雷奥公司在智能天线系统、智能钥匙、开关和机械控制盘等零部件系统都广泛采用卡扣连接，并利用分析软件进行仿真模拟，同时评估结构失效的风险，确保了所设计的卡扣的卡接力和拉脱力满足相关要求。

通过有限元分析方法，在设计阶段，就可以模拟和验证所设计的卡扣卡接力是否满足相关标准要求。通过力学分析软件中的优化模块，以卡接力为优化设计目标[3-4]，利用基于力学分析的优化设计，得到卡扣主要结构尺寸、卡扣宽度和卡扣高度与优化目标卡接力(对应于变形量)之间的定性关系。最后利用曲线拟合方法[5-6]，得出卡扣高度这一主要结构尺寸与设计目标卡扣卡接力之间的函数关系，为结构设计工程师在卡扣结构设计过程中提供参考。

1 数值模拟与优化过程

1.1理想化模型

根据如图1所示的一种卡扣的基本结构，进行卡扣卡接时，假设需要两个卡扣和一个卡板。分析过程如下：(1)分析卡接瞬间之前的过程，也即卡板上表面在受到垂直于上表面的卡接力的情况下，沿卡扣斜面向下移动，忽略卡扣与卡板之间的摩擦；(2)以一对卡扣卡接情况进行分析，并忽略卡板的自身重力；(3)计算结果表明，同一方向上卡扣的变形量与卡板的变形量相差两个数量级，因此忽略卡板的变形量；(4)假设卡板长度和卡扣下端间距相同，卡接过程中，分析卡扣在卡接瞬间的极限变形情况，将其作为分析卡板受卡接力沿卡扣斜面向下移动时整个结构的情况。

图1 一种卡扣的基本结构尺寸

1.2 参数说明

基于上述假设，计算、分析和优化以卡扣高度H和卡扣宽度W为输入变量的情况，如图2所示，优化结果为卡扣的变形量。这一优化参量直接决定了卡扣卡接的容易程度，间接决定了卡扣的卡接力和卡扣根部应力状况。以卡扣高度H和宽度W为设计变量，其中在数值模拟阶段，其施加的载荷力是根据卡扣极限位移为条件产生的变形反推出来，并施加于分析对象上。通过该方法，可以得到其他几组不同尺寸结构的卡扣卡接时候的最小卡接力(如图2所示)、极限变形、卡扣根部和卡板上的最大应力值。如表1所示，同时给出了所用材料的名称。表1中卡扣根部和卡板的应力是数值模拟计算得出的结果。

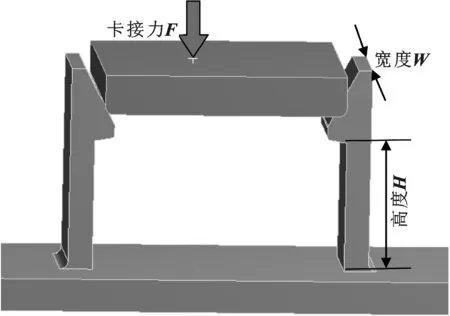
图2 参数化尺寸卡接力F、高度H和宽度W

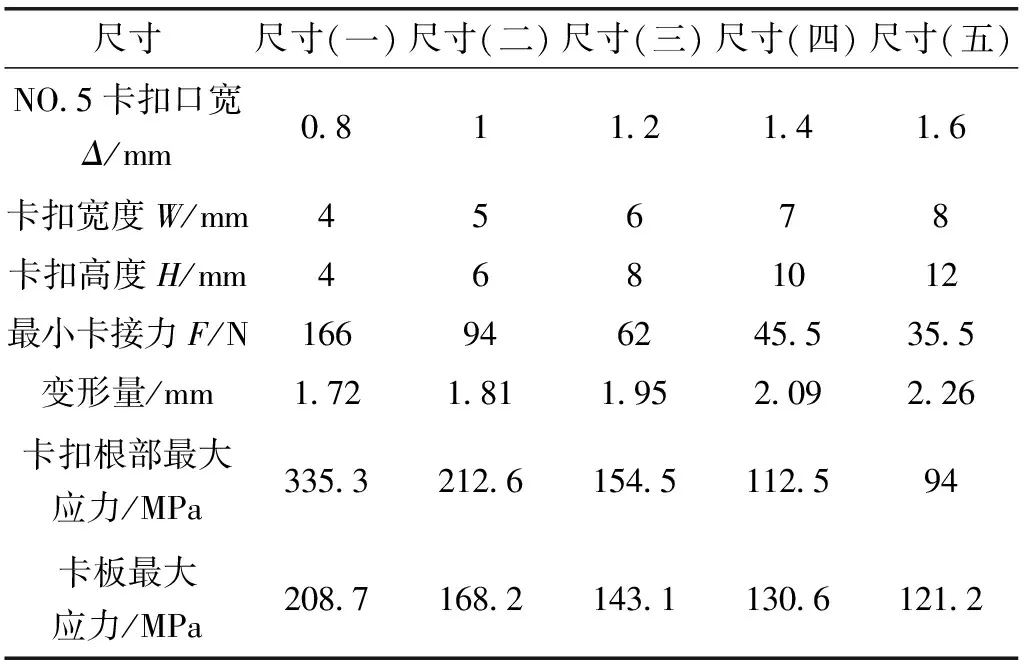
表1 不同结构尺寸卡扣数值模拟结果

注：卡板和卡扣材料均为ABS。

1.3 优化设计过程

根据参数说明，卡扣各个结构尺寸中卡扣高度和宽度未给定，其他结构参数都是给定的。优化目的就是找到两个未知参数与目标参数卡接力(变形量)之间的关系，为结构设计提供参考。

参照图1的结构尺寸，以表1的第一列结构尺寸为基本尺寸，并以卡扣高度H和卡扣宽度W为设计输入变量。利用优化设计相关模块进行求解。首先可以得到设计过程中各个设计变量之间的相关性，同时可以得到实验设计点数据。在结构设计中，由于受到零部件的整体性、安装性以及制造工艺原因，一些结构尺寸的设计上下限被规定下来，例如对于汽车的前室内灯，其两个卡扣之间的距离决定了灯具的总宽度，卡扣的总高度有一定限制不至于产生碰撞和干涉。根据上述两个原因，进行结构的优化设计[7]，得到一组实验设计点，如图3所示。同时得出两个设计输入参数的实验设计点，如图4和图5所示。

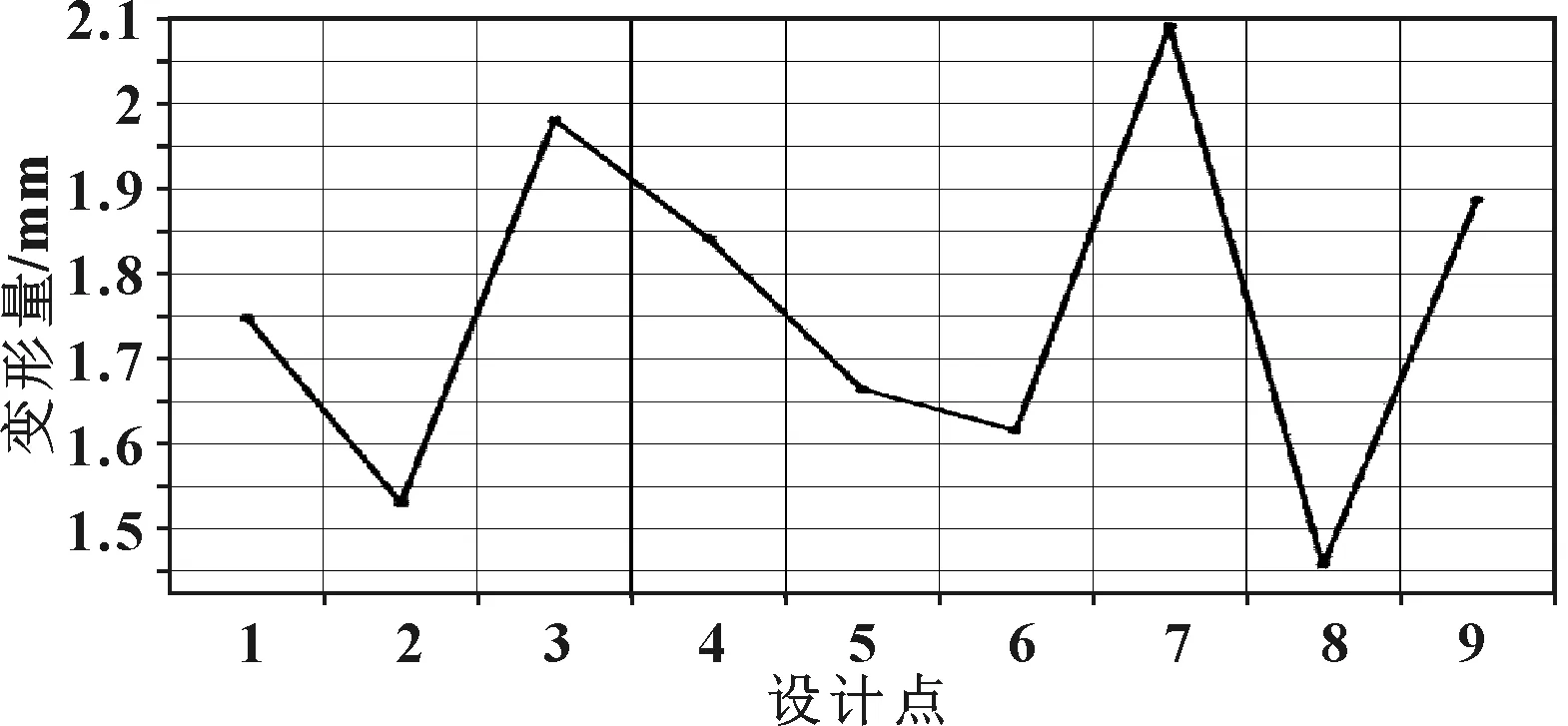
图3 卡扣变形的设计点

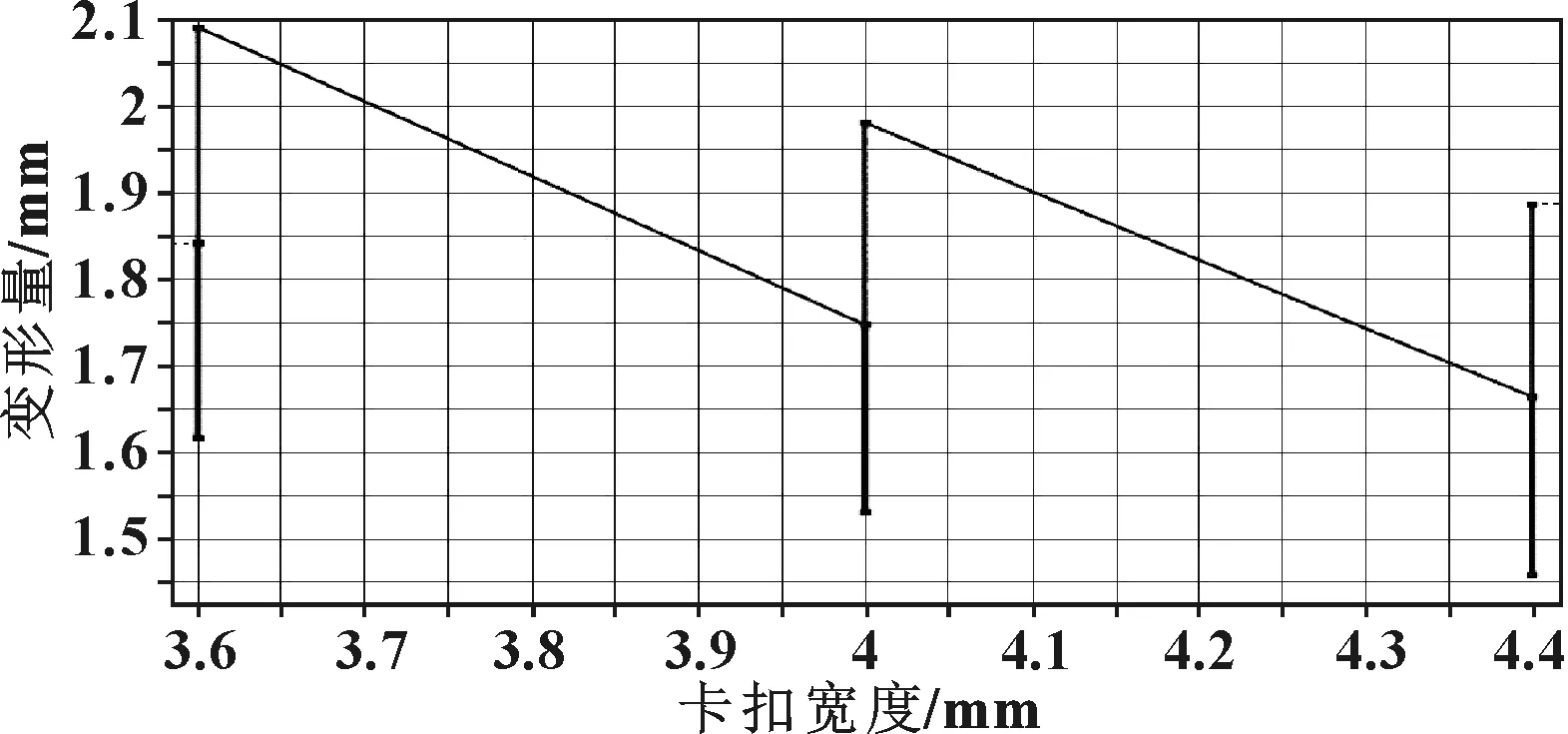
图4 卡扣宽度与变形量的实验设计点

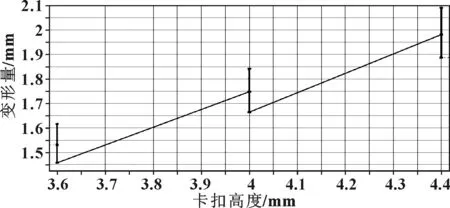
图5 卡扣高度与变形量的实验设计点

对于卡扣的卡接，容易发现卡扣越高，越容易卡接；卡扣较宽，卡扣较难卡接。卡扣高度和宽度这两个尺寸都对卡接有影响。

图6、图7分别给出了上述两个参数的二次曲线决定度矩阵图和决定度系数直方图。从图6可以看出，如果想让卡扣容易卡接，主要取决于卡扣的高度参数H；而从图7可以读出，卡扣高度H决定度系数为78%，另外一个参数卡扣的宽度W，其决定度系数仅仅约为14%。由此知道，卡扣容易卡接与否，主要由卡扣高度决定。由“分析力学”知道，当卡扣较高时，刚度较低，容易产生变形，从而实现卡接。

图6 二次决定度矩阵

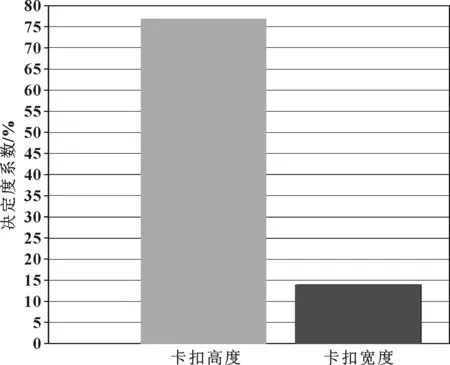
图7 两个输入参数与优化目标输出参数(变形量)之间的决定度系数柱状图

图8给出了两个设计参数与目标参数的线性相关性矩阵。由图8可知，卡扣高度H与容易卡接程度(变形量)成系数约为0.8的正线性相关；而卡扣宽度W与容易卡接程度成负的线性相关，相关系数约为-0.3。说明，宽度越宽，卡扣越不容易实现卡接。

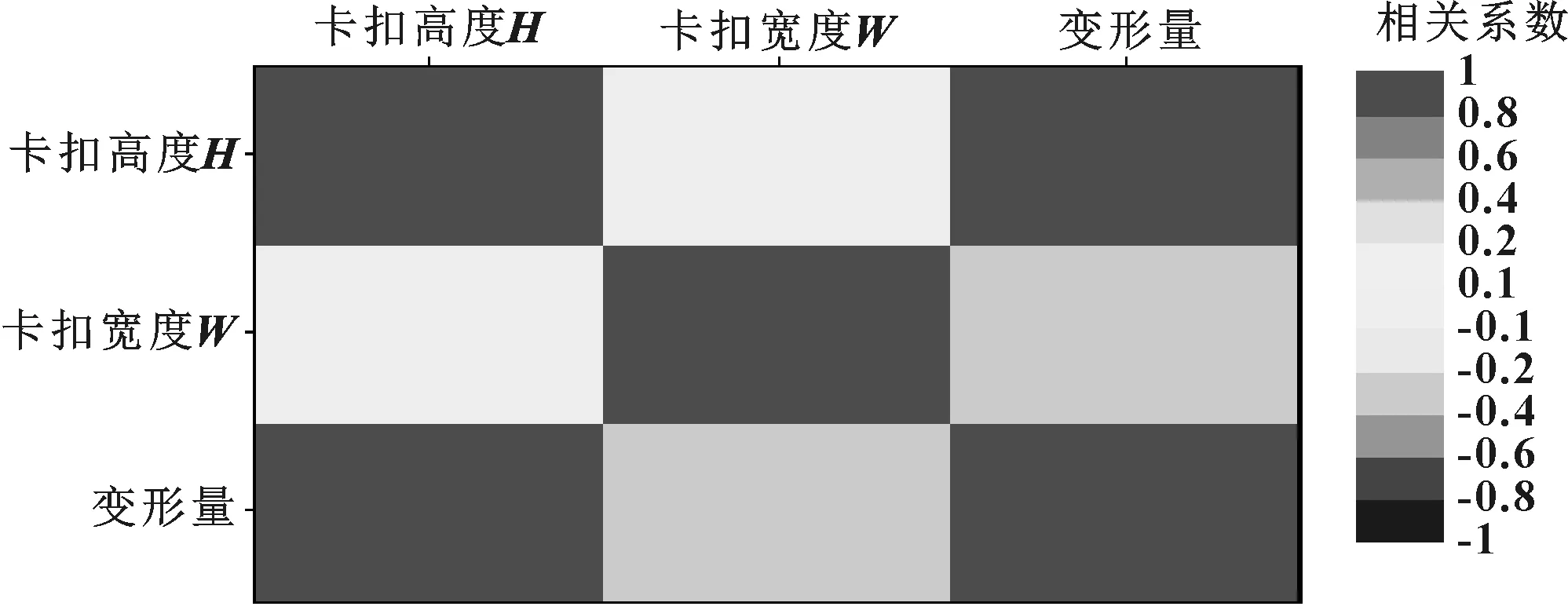
图8 线性相关矩阵

图9和图10分别给出了卡扣宽度W和卡扣高度H与卡扣卡接容易程度具体的相关性离散化程度，其中包含了线性相关度和二次相关度曲线。

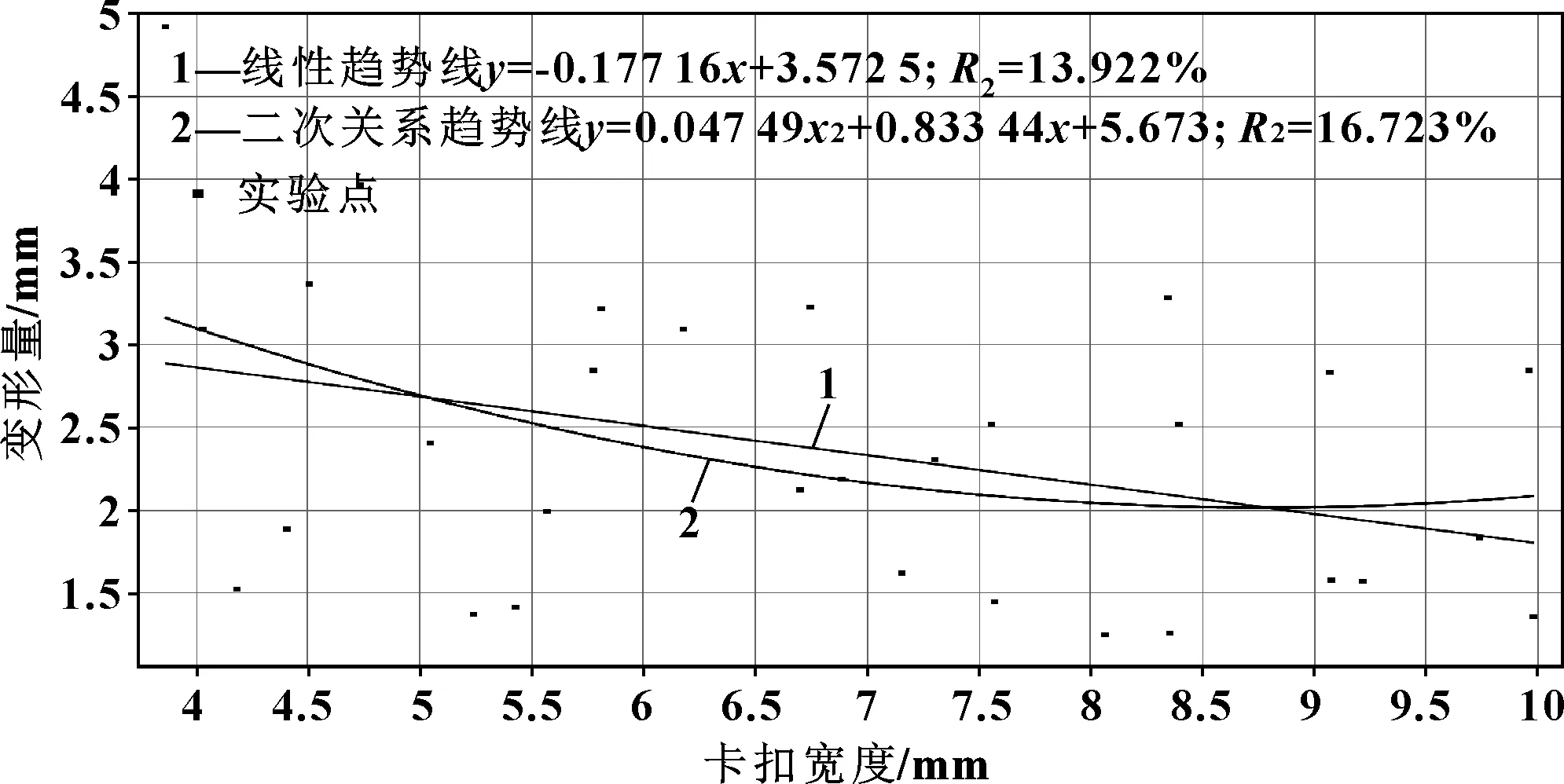
图9 卡扣宽度与变形量之间的相关性(线性相关和二次相关)

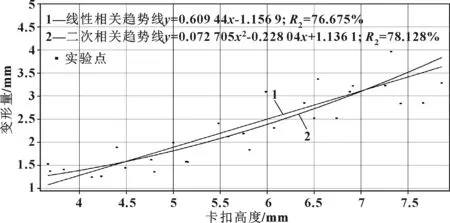
图10 卡扣高度与变形量之间的相关性(线性相关和二次相关)

在进行卡扣结构设计过程中，通过尺寸的确定来改变零部件的结构特征，同时也改变了所设计的零部件的力学性能参数。设计过程中，会有许多参数会对力学性能产生影响。但究竟哪个结构参数的影响程度最大，或者对卡扣而言，究竟哪个参数对力学性能更敏感，图11给出了两个参数对设计目标参数的敏感度。从图11可以看出，卡扣高度这一参数对设计目标最敏感，敏感度约为91%，而卡扣宽度对设计目标的敏感度不到0.05%。这样可以直观地指导结构设计师在设计过程中，如果想通过改变结构尺寸来改变卡扣容易卡接程度，那么改变卡扣高度H这一结构尺寸最有效。

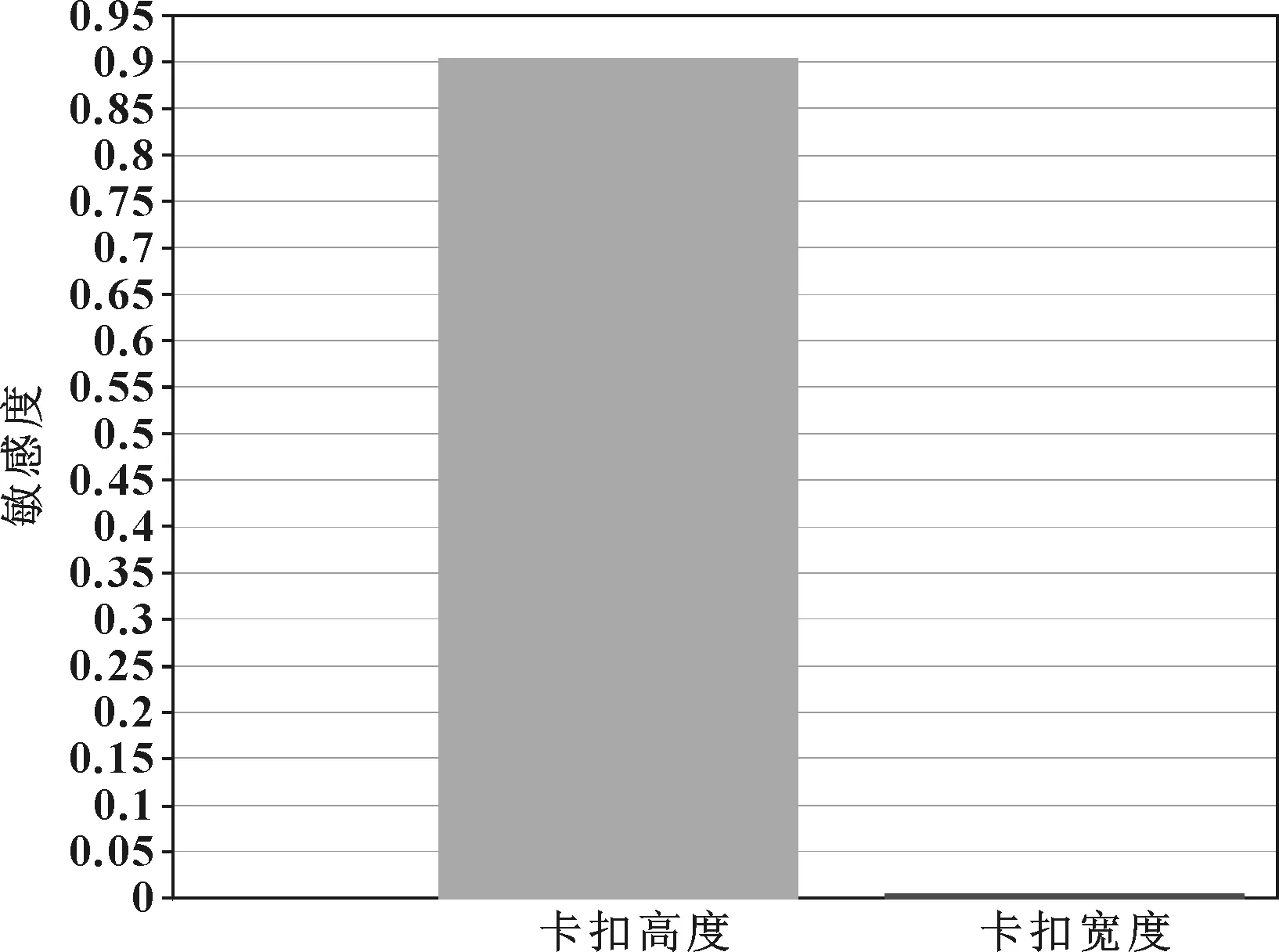
图11 两个输入参数的敏感度图

图12是卡扣卡接极限状态的应力图，其他结构尺寸相同，其左侧的卡扣高度H1要大于右侧的卡扣高度H2。从应力云图中看出，在卡扣卡接过程中，卡扣根部出现应力集中[8]，且最大应力已经超过了材料的屈服应力，但是由于卡接是个瞬时过程，卡扣不会出现断裂危险。但是实际样件中，经过卡接的样件，其卡扣根部仍然会有泛白现象，这是由于材料应力过大屈服造成的。

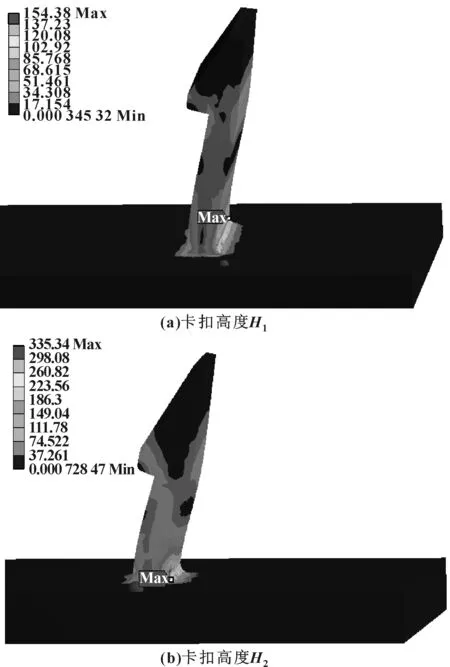
图12 两种不同高度尺寸的卡扣应力云图

1.4 卡扣高度与卡接力之间的关系

以卡扣高度H为单一变量，且变量区间定为[4,12]。同时固定卡扣的其他尺寸，包括卡口宽度Δ=0.8 mm，卡扣宽度W=4 mm，卡扣和卡接板材料仍然为ABS。与此同时，取变量“卡扣高度H”的固定变化步长为2 mm，得到仿真实验点，如表2所示。

表2 以卡扣高度H为单一变量的设计实验点

注：卡扣和卡板材质均为ABS。

表2中数据是利用有限元分析软件中静态结构分析得到的数值模拟结果。将各个实验设计点用平滑曲线连接，并分别用线性、指数函数和幂函数进行曲线拟合，得到如图13所示的关系。同时给出了满足线性、指数函数和幂函数的具体函数关系式。从图13中可以看出，卡扣高度与卡接力之间最接近幂函数关系，其幂函数关系式为

y=4 876.7x-2.408

(1)

从幂函数拟合曲线看出：卡扣的高度越高，曲线的拟合度越好。

在进行卡扣设计过程中，如果已知高度尺寸x，利用式(1)可以估算得到该尺寸下，卡扣卡合所需要的最小卡接力的具体数值。

在卡扣卡接过程中，优化目标使相同卡接力情况下更容易卡接。但在实际卡接过程中，从卡扣和卡板的应力应变图中可以看出，卡扣最大应力处(卡接接触点)的值已经远远大于材料的屈服应力。在这种高应力和应变情况下，材料已经发生塑性变形。因此在卡扣和卡板的相应位置，会出现类似于磨损的现象。

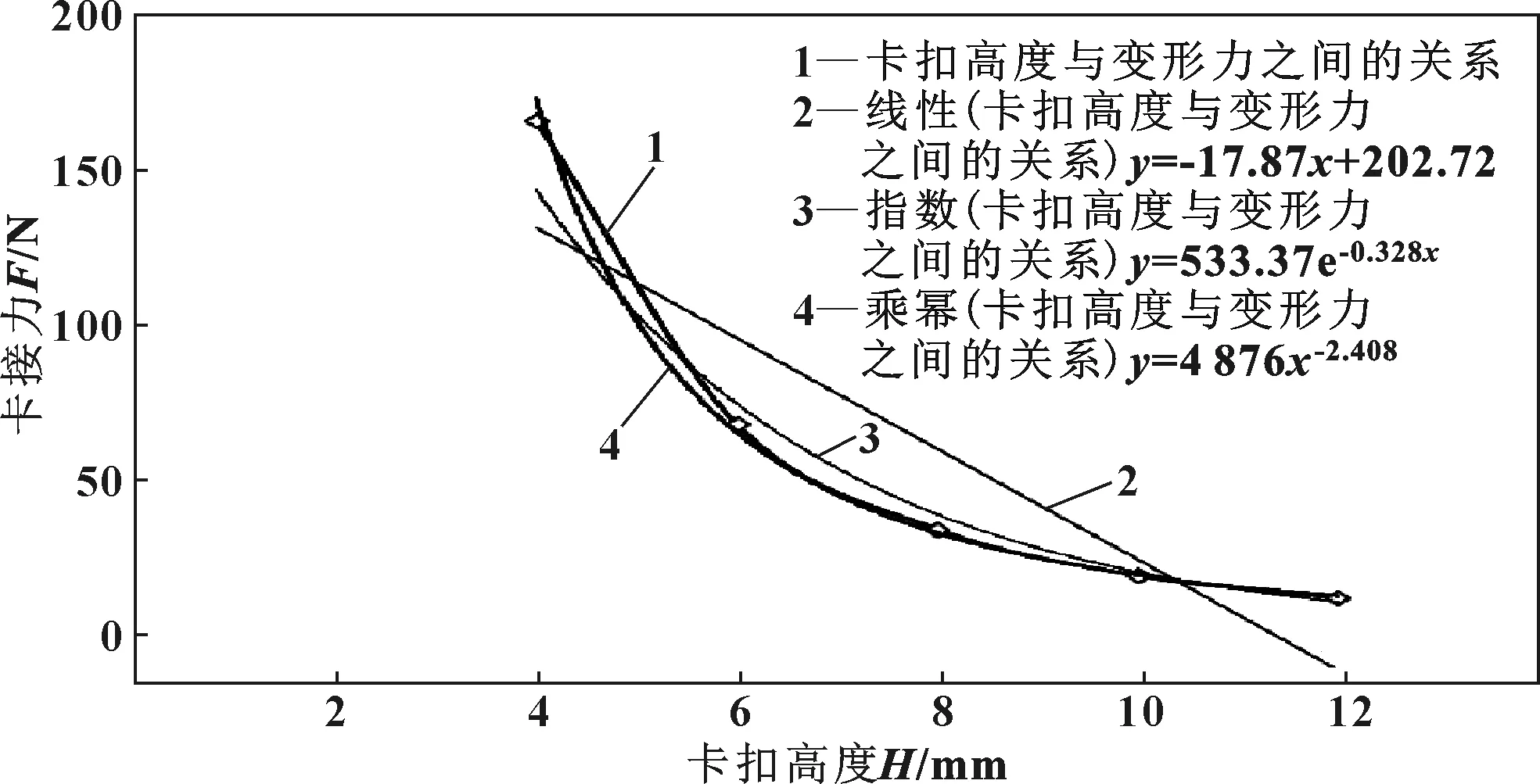
图13 卡扣高度与卡接力之间的函数关系

2 结论

根据数值模拟计算结果及优化结果，得到如下结论：

(1)为了满足相关法规对卡接力的要求，首先考虑卡扣的高度。通过改变这一结构尺寸，能快速并有效地改变卡接力，达到法规要求；增加卡扣高度，可以减少卡扣根部应力，防止卡扣根部应力集中产生潜在裂纹，后续在行车振动中，裂纹会扩张，从而产生松动、噪声或者断裂危险；

(2)卡扣宽度减小，对应力影响不大，它只与扣合处强度有关；卡扣宽度增加，卡扣强度增加，卡扣卡合需要的卡接力增加，但是变化微小[9]。