基于自抗扰控制的永磁同步电机弱磁控制策略

李思毅 苏健勇 杨贵杰

基于自抗扰控制的永磁同步电机弱磁控制策略

李思毅 苏健勇 杨贵杰

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

针对应用纯积分器的电压反馈弱磁控制在弱磁程度较深时会发生振荡乃至失控的问题，提出一种基于自抗扰控制的电压反馈弱磁控制方法。通过建立电压环小信号时域模型，设计了自抗扰电压控制器，给出控制器参数的选取原则并利用描述函数法对稳定性进行分析。该方法不依赖被控对象精确模型，鲁棒性强，可有效观测并补偿系统中存在的非线性及其他扰动因素，有效处理线性与非线性控制对象。实验证明，与纯积分器方法相比该文所提方法在弱磁深度较深时带载能力更强，稳定性更好。

永磁同步电机 弱磁控制 自抗扰控制 描述函数法

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因其效率高、功率密度高、起动转矩大、调速范围宽等优点被广泛应用于家用电器、交通运输、工业自动化等领域[1-2]。为了兼顾宽调速范围和大转矩输出能力的要求，在逆变器输出到达极限时常采用弱磁控制进一步提升电机转速。

传统弱磁控制方法主要包括前馈弱磁方法、反馈弱磁方法和混合弱磁方法。前馈弱磁方法基于电机数学模型调节定子电流矢量的参考值，一般通过直接计算法[3]和离线表格法[4-5]实现；反馈弱磁方法利用过调制前后的dq轴参考电压差[6]或直接利用dq轴参考电压调节d轴电流或超前角的参考值[7]；混合弱磁方法将前馈弱磁方法和反馈弱磁方法相结合，系统中既有前馈通道，也有反馈通道，响应速度快于反馈弱磁方法，可抵抗电机参数变化带来的影响[8]。三种方法中前馈弱磁方法响应速度最快，但其控制性能依赖电机参数的准确性。混合弱磁方法结合了前馈弱磁方法和反馈弱磁方法的优点，但增加了控制结构的复杂程度。反馈弱磁方法响应速度适中，控制结构简单，对电机参数依赖性小，应用广泛[9]。

传统电压反馈弱磁控制方法一般使用纯积分控制器，其结构简单，易于实现，可实现稳态情况下的无差跟踪。但积分器的存在会给系统带来副作用[10]，高速情况下纯积分器方法会因反电动势、磁饱和等非线性因素使系统振荡甚至失控[11]。为了克服基于纯积分器方法的缺点，近些年学者们对非线性电压反馈弱磁控制进行了进一步研究。文献[11]基于小信号模型提出了同时适用于电动状态和发电状态的自适应弱磁方法，该方法在不同弱磁模式、不同特征电流比值情况下均能稳定运行。文献[12]利用模糊速度控制器进一步提高文献[11]中方法的电压利用率与弱磁能力。文献[13]通过非线性增益补偿实现了基于超前角的自适应弱磁控制，部分克服了电压环非线性特性。文献[14]在文献[13]的基础上将转矩参考值引入电压环，并且将d轴电流参考值变为输出，实现了速度环与电压环的解耦，保证了转矩控制的准确性。文献[15]进一步考虑了输入电压降低、电机加速、瞬态转矩变化等动态条件对弱磁控制的影响，提出了电压控制器与相关参数的设计原则。以上方法虽然有效地解决了电压环非线性特性带来的问题，但没有消除积分器产生的负面影响。

自抗扰控制（Active Disturbance Rejection Control, ADRC）可克服积分器在控制系统中的固有缺点，并且可以有效观测并补偿系统中存在的非线性及其他扰动因素，统一处理线性与非线性控制对象。目前已在PMSM伺服控制中取得了较好的应用效果[16]。文献[17]针对速度滤波器对转速调节带来的负面影响，提出基于扩张状态观测器和基于锁相环观测器的自抗扰控制器。基于扩张状态观测器的方法能更好地抑制测量噪声，基于锁相环的方法鲁棒性和噪声抑制特性稍差，但具有更好的低频干扰抑制能力。文献[18]采用线性/非线性切换的自抗扰控制器实现速度与电流控制，与线性ADRC相比采用线性/非线性切换的方法可在同样抗干扰能力下降低扩张状态观测器的增益，并且转速响应超调更小，电流跟踪性能好。文献[19]将三环控制简化为双环控制，采用二阶非线性ADRC控制器实现外环位置与转速复合控制，在内环利用一阶线性ADRC控制实现电流控制，该方法有效地提高了系统抵抗负载扰动和参数变化的能力。文献[20]利用扩张状态观测器代替滑模观测器观测扩展反电动势，并且在内环采用ADRC电流控制器，该方法不需要电机磁链参数，没有滑模观测器带来的抖振与滞后，避免了低通滤波器和角度补偿带来的副作用。ADRC在速度控制、电流控制、位置控制、反电动势观测等方面均表现出优越性，这些优点同样适用于电压反馈弱磁控制。

针对基于纯积分器的传统电压反馈弱磁控制存在的缺点，本文提出一种基于自抗扰控制的电压反馈弱磁控制方法，并利用描述函数法分析方法的稳定性。所提方法将由定子电压和d轴电流参考值引起的扰动，以及忽略的电阻压降、逆变器非线性特性等因素视为总扰动，进行较好地观测并补偿。与传统纯积分器方法相比，所提方法可拓宽电机的运行范围，增加带载能力，提高弱磁区域内的稳定性。

1 PMSM数学模型

表贴式永磁同步电机在dq两相旋转坐标系下的数学模型为

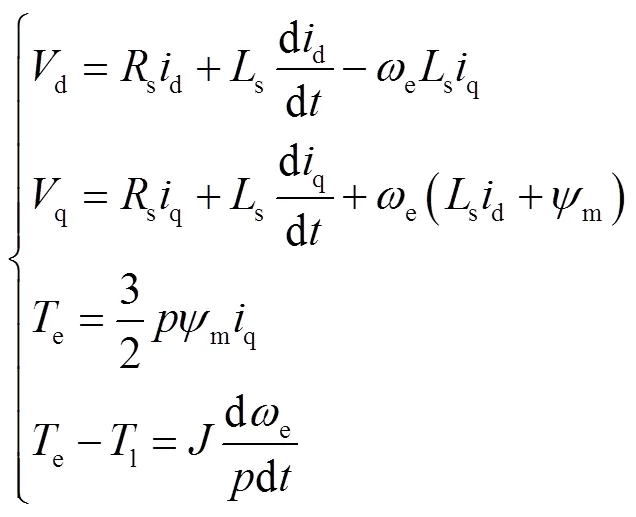
电机运行时需受到逆变器输出和电机额定电流电压的约束，可表示为

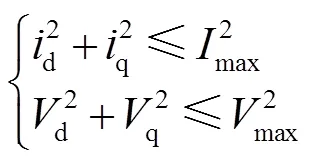
稳态运行时可忽略电阻压降及微分项，式（1）中定子d、q轴电压可表示为

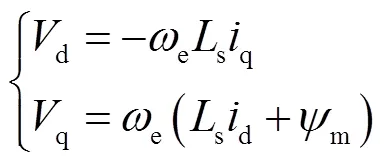
将式（3）代入式（2）中的电压约束，可得到电压极限圆表达式为

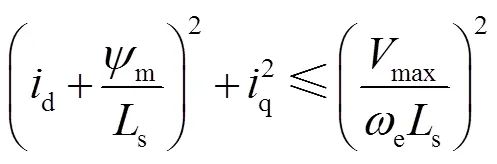
根据式（2）中第一项和式（4），可在dq坐标系中画出电流极限圆与电压极限圆，如图1所示。

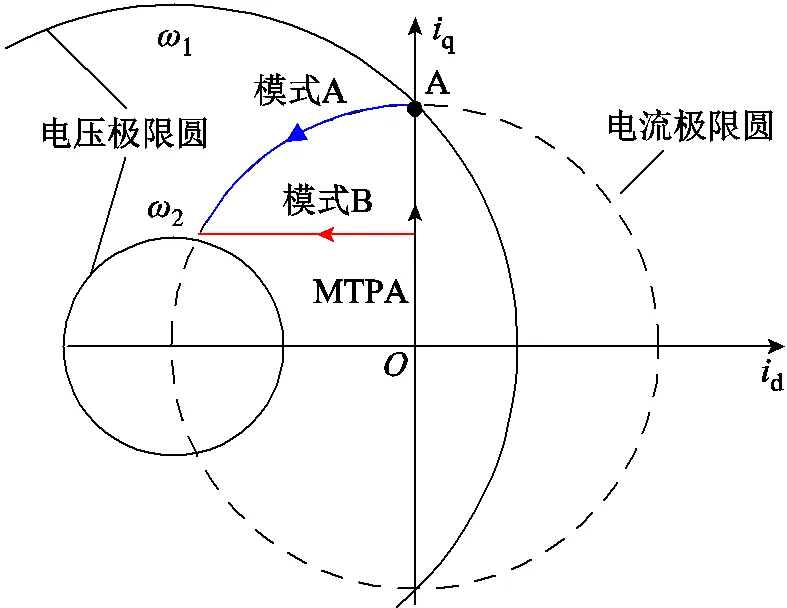
图1 电压极限圆与电流极限圆

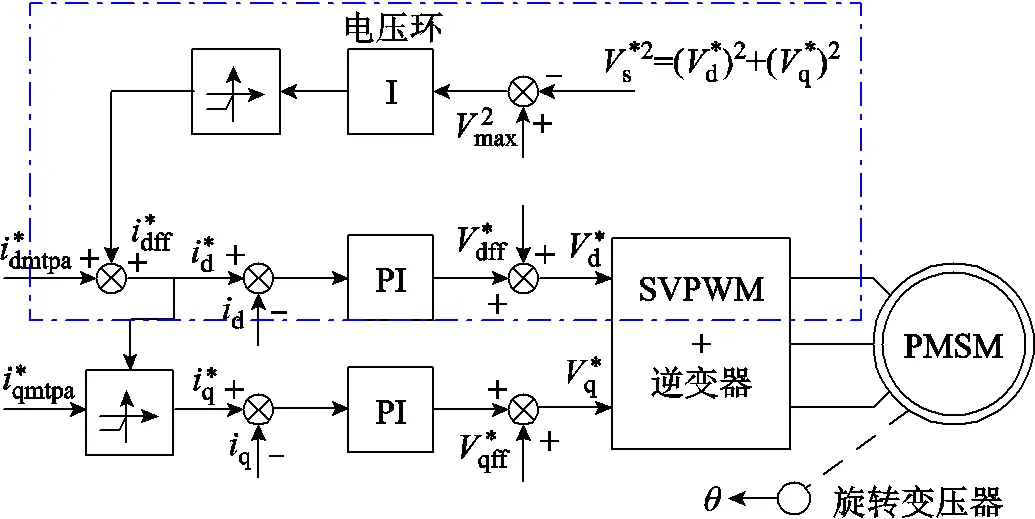
图2 传统纯积分电压反馈弱磁方法

利用小信号分析法，在工作点附近可得到等效电压环小信号模型如图3所示[11,14]。

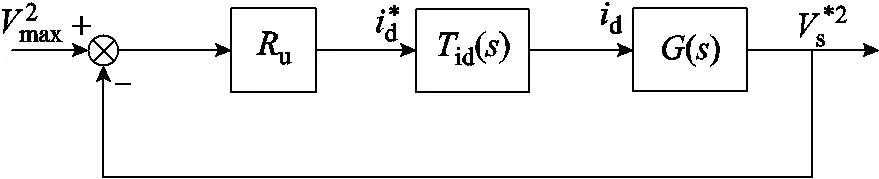
图3 等效电压环小信号模型

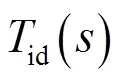
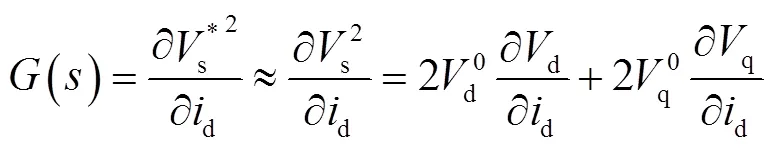
由于

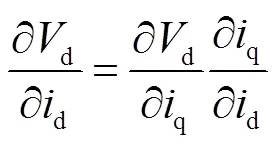
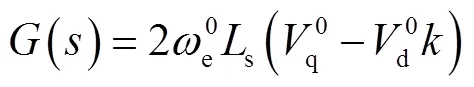
因此，被控对象的传递函数可表示为

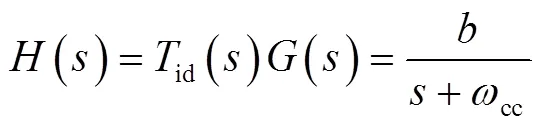
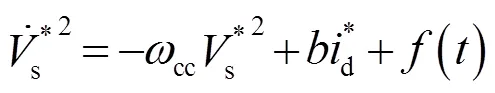
将系统化简为

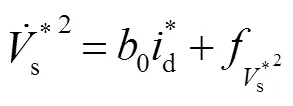
2 电压环ADRC控制器

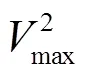
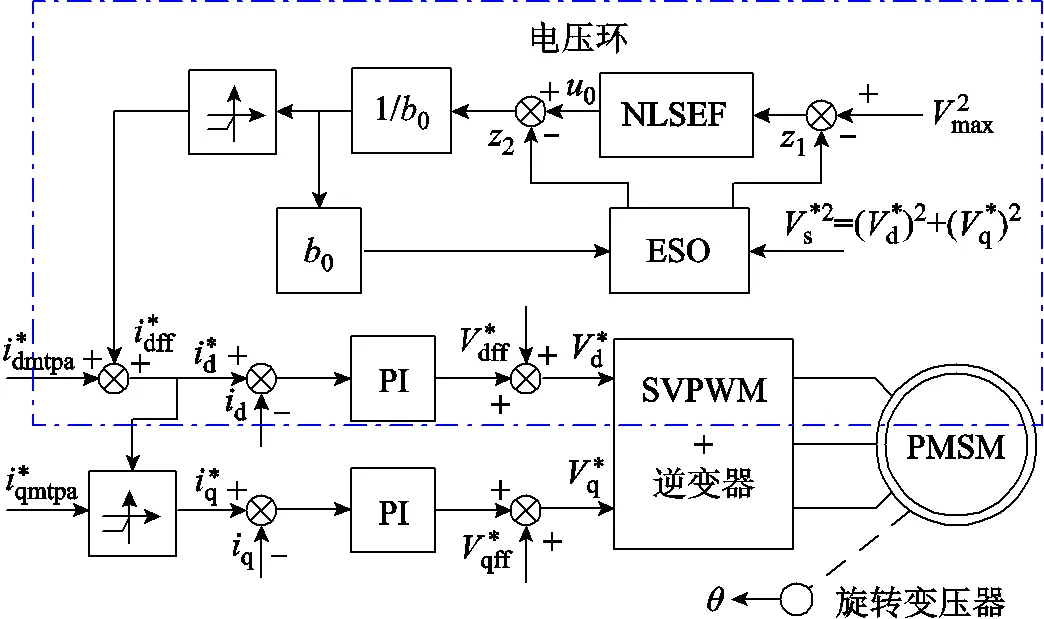
图4 基于ADRC的电压反馈弱磁控制方法

2.1 一阶电压环ADRC控制器设计

2.1.1 ESO设计

对一阶被控对象

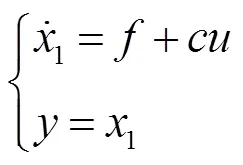
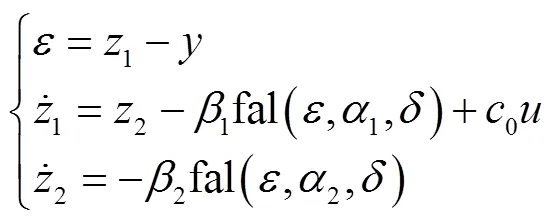
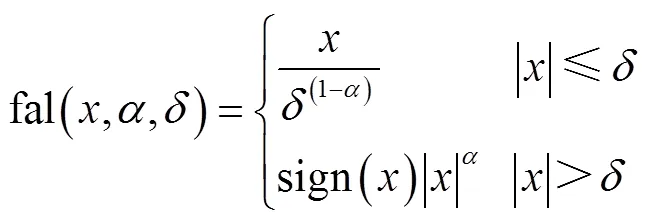
式中，sign()为符号函数。

根据式（10）～式（14）可建立ESO。

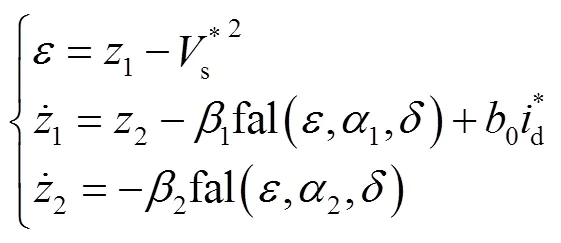
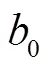
模式A

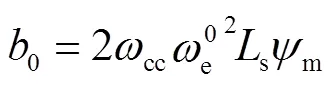
模式B

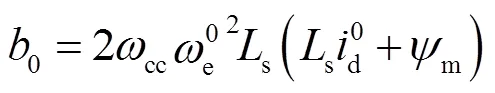
表1 永磁同步电机参数

Tab.1 The parameters of PMSM

两种工作模式下的0与转速、d轴电流的关系如图5所示。

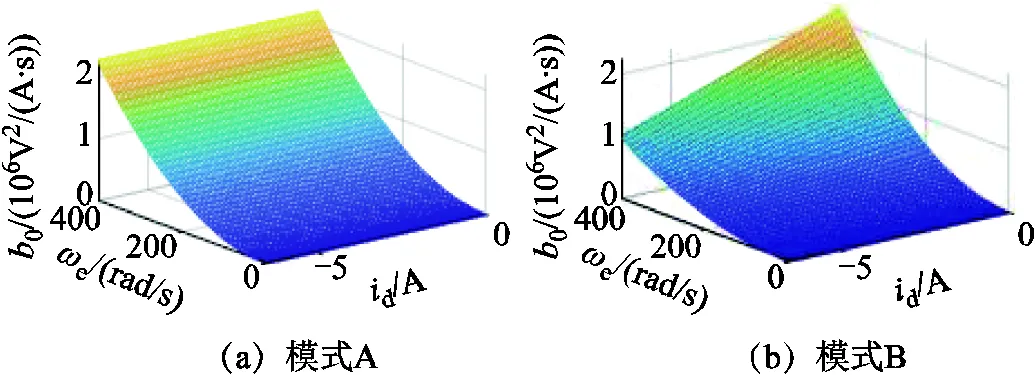
图5 两种弱磁工作模式下

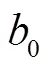
2.1.2 NLSEF设计

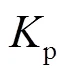
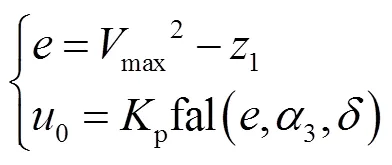
ADRC利用ESO对上述扰动统一观测和补偿，通过非线性反馈使系统化为积分器串联标准型。

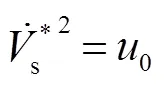
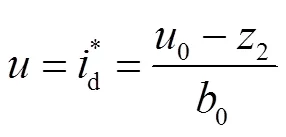
根据式（9）、式（15）、式（18）、式（20）可得到一阶电压环ADRC控制器，如图6所示。

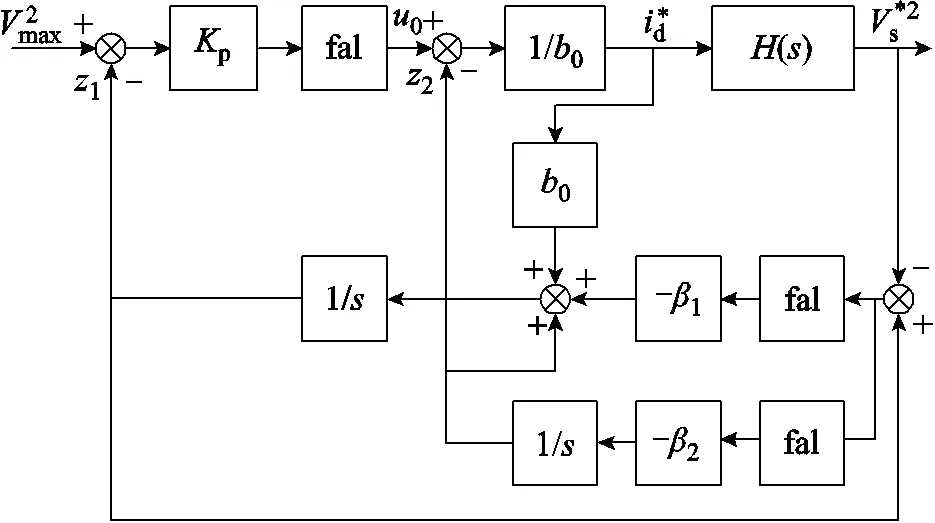
图6 一阶电压环ADRC控制器

2.2 一阶电压环ADRC控制器稳定性分析

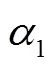
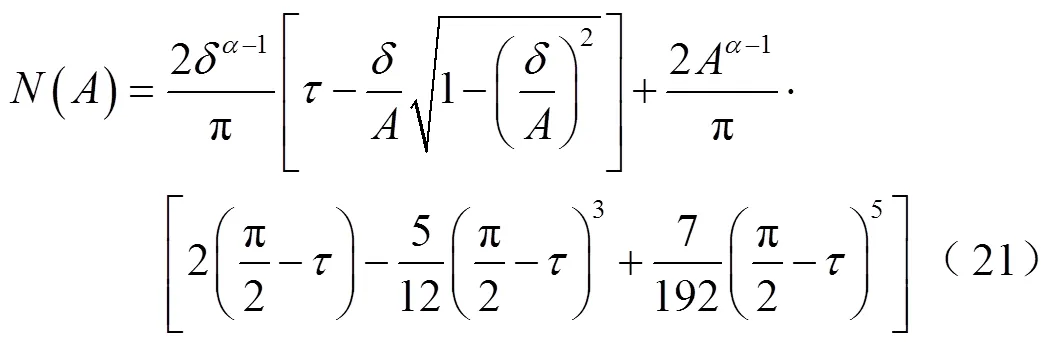
图6描述的闭环传递函数为

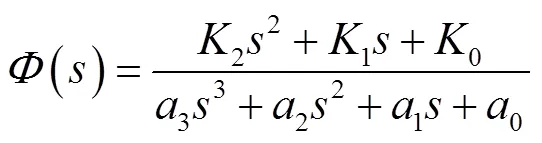
式（22）各系数取值见附录式（A1），前向通道和各回路传递函数见附录式（A2）。

根据闭环极点相等的原则可对式（22）进行简化，如图7所示。

图7 非线性系统简化结构

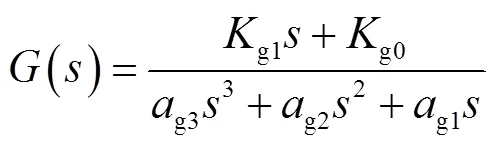
式（23）各系数取值见附录式（A3）。

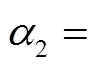
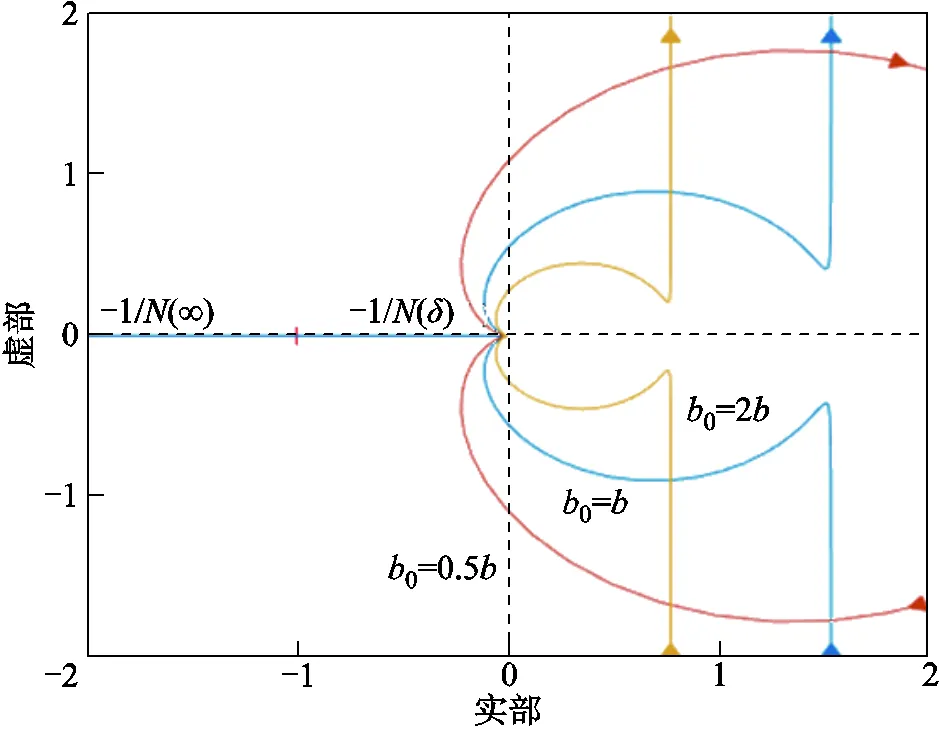
图8 线性部分Nyquist曲线和非线性部分曲线

3 实验结果

为了对比ADRC电压环控制器和纯积分控制器的弱磁效果，验证基于ADRC的弱磁控制方法的有效性。本文针对空载起动、带载起动、突加负载三种工况进行测试，实验电机参数与控制参数见表1、表2。实验平台如图9所示，主控芯片采用英飞凌XMC4800，控制频率和开关频率为10kHz，使用DL850示波器和EtherCAT总线采集数据。

表2 ADRC与纯积分器参数

Tab.2 The parameters of ADRC and pure integrator

图9 实验平台

3.1 空载起动

速度给定为两倍额定转速，电机空载起动，传统纯积分器方法与ADRC方法的速度、dq电流、定子电压波形如图10和图11所示。

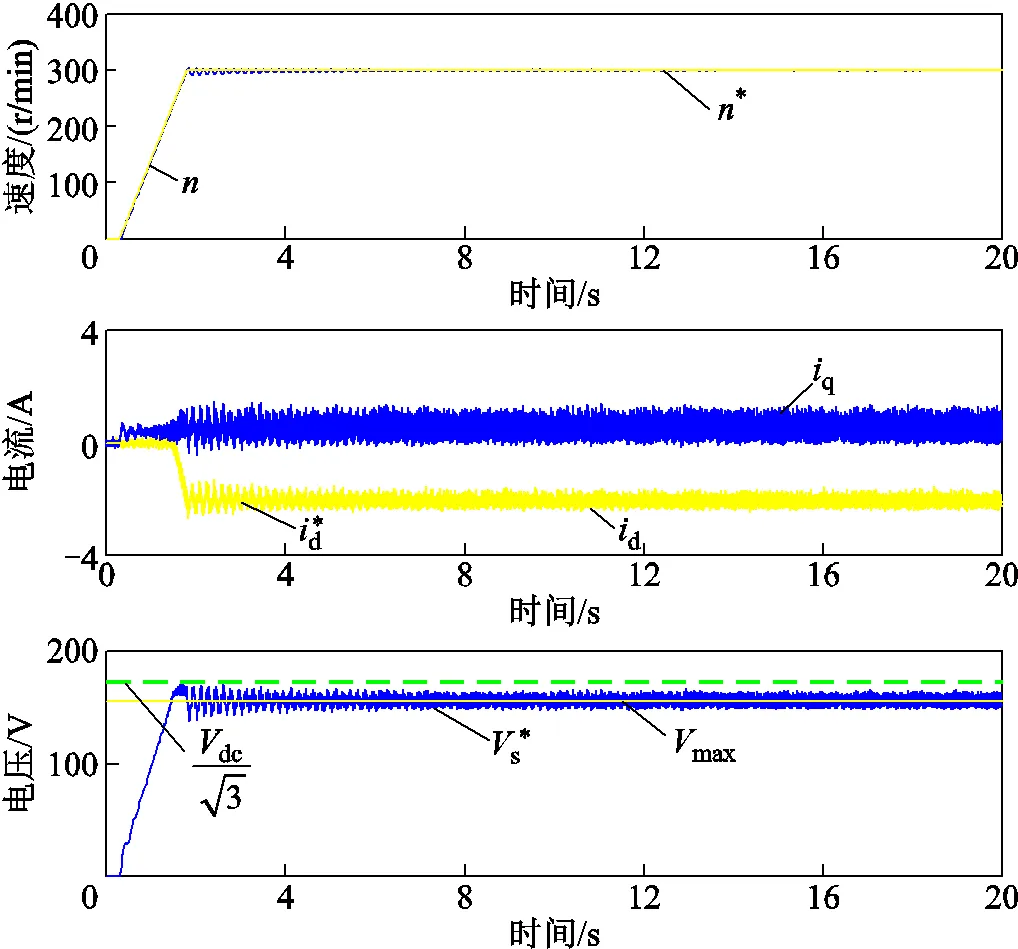
图10 纯积分器方法空载起动实验波形

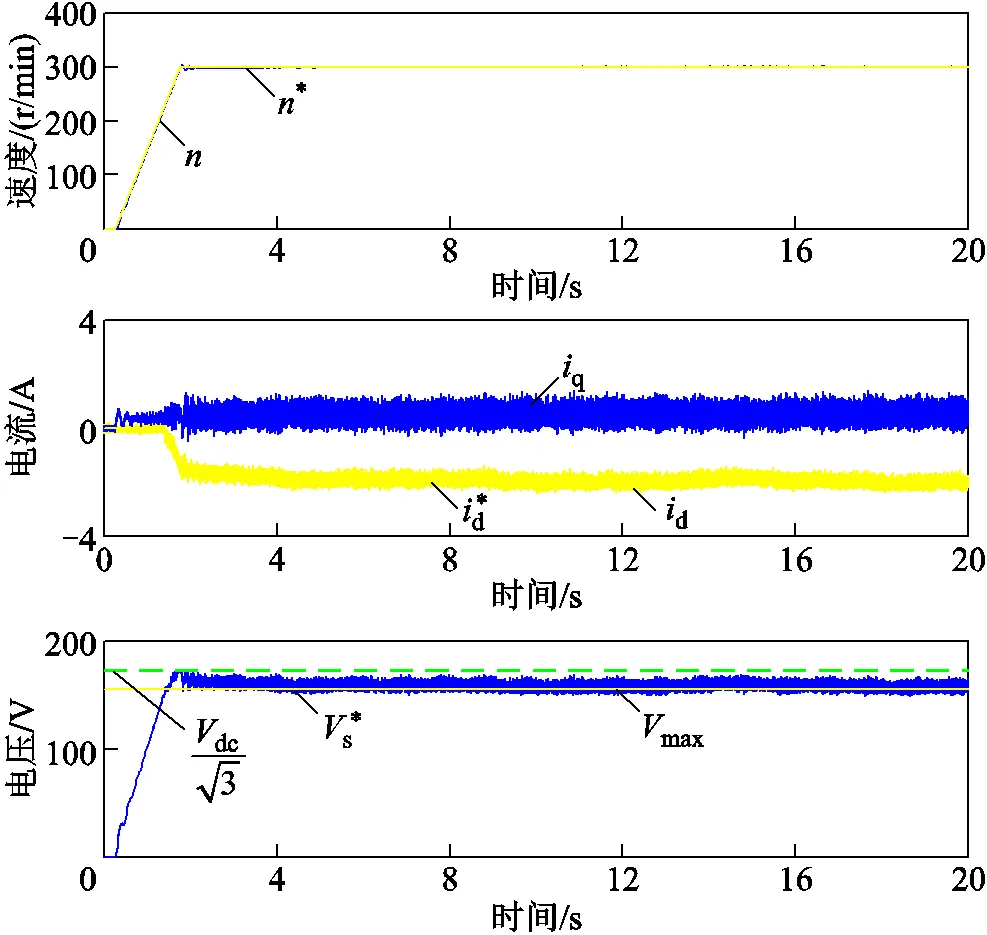
图11 ADRC方法空载起动实验波形

对比图10和图11可知，纯积分器方法存在明显的电压与转速波动，而ADRC方法电压与转速波动较小。达到稳态后纯积分器方法和ADRC方法的d轴电流平均值与波动幅度基本一致。图10和图11说明在空载起动至相同转速的工况下，ADRC方法电压和转速更稳定，不易失控。

3.2 带载起动

速度给定为两倍额定转速，电机带载起动。ADRC方法在带载工况下的响应波形如图12所示。从图12中可以看出，受负载影响，电机转速动态响应变慢，进入稳态后，与空载相比电机d轴电流负向增加，q轴电流正向增加，定子电压波动幅度增加。

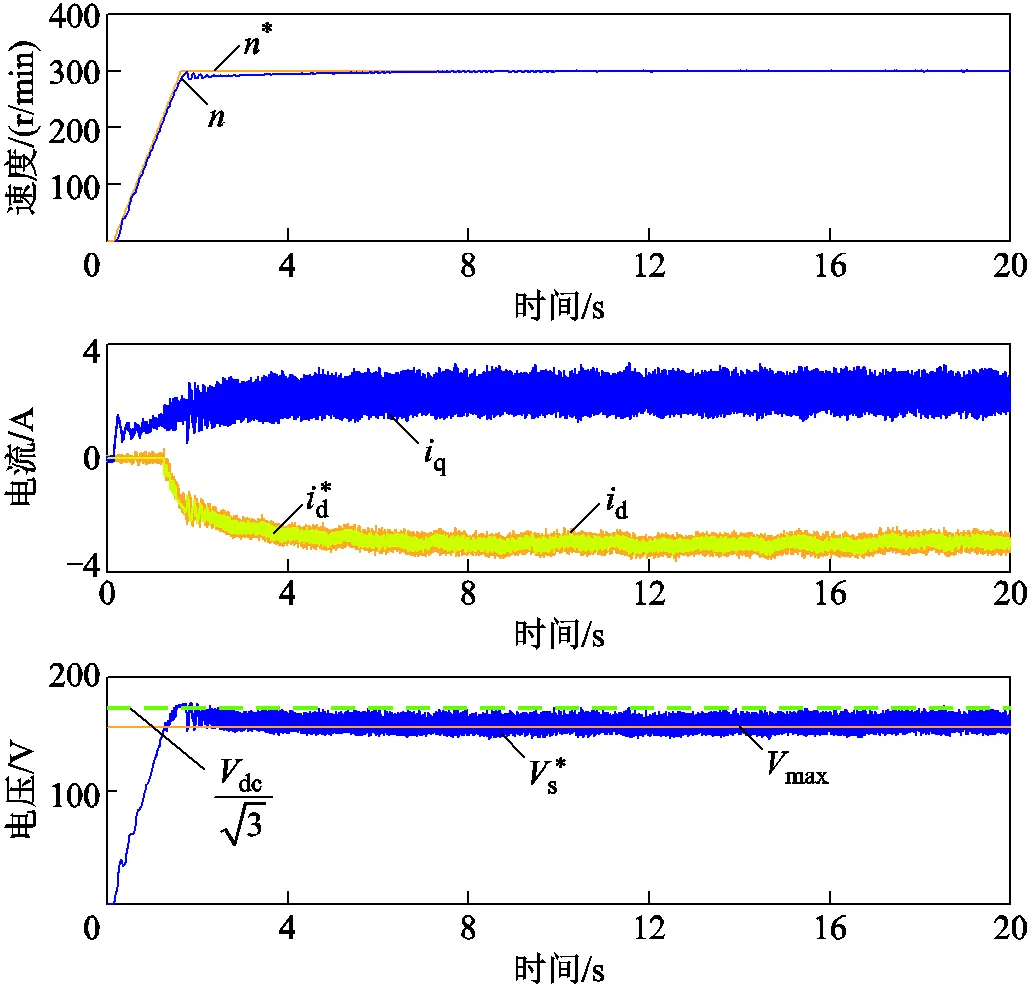
图12 ADRC方法带载起动实验波形

纯积分器方法带载起动在速度达到给定后直接失控，转速、电流与定子电压均大幅度振荡。图12说明带载后电机工作点向左上方移动，ADRC方法在带载工况下可以稳定运行，而纯积分器方法无法在两倍额定转速给定的工况下带载起动。

3.3 突加负载

速度给定为两倍额定转速，电机空载起动。纯积分器方法与ADRC方法在突加负载工况下的响应波形如图13和图14所示。图中1.4s时进入弱磁区域，7.3s时增加30%额定负载，14.9s后ADRC方法稳定运行于弱磁区域。由图13与图14可以看出，加载前ADRC方法转速收敛更快，波动更小，d轴电流给定值波动较纯积分器方法更大，但dq轴电流波动与纯积分器方法几乎一致，定子电压波动和超调明显更小。两种方法转速超调均为5r/min，在空载稳态时的电压波动幅度基本相同。

加载后两种方法转速均下降约9r/min，纯积分器方法的转速、电流、定子电压波动逐渐增加最终失控。而ADRC控制的转速波动无明显变化，d轴电流波动保持不变，定子电压幅值有明显上升但仍在给定附近并逐渐下调。

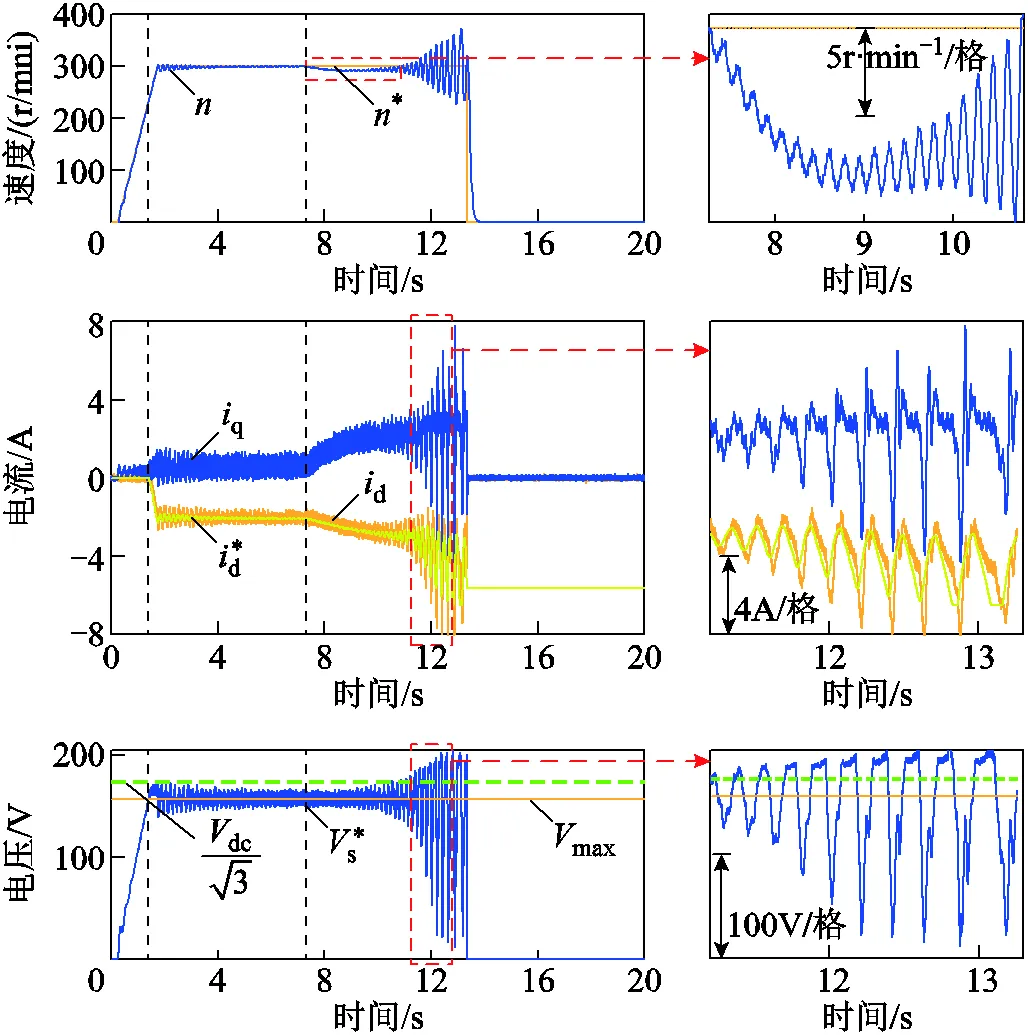
图13 纯积分器方法突加负载实验波形

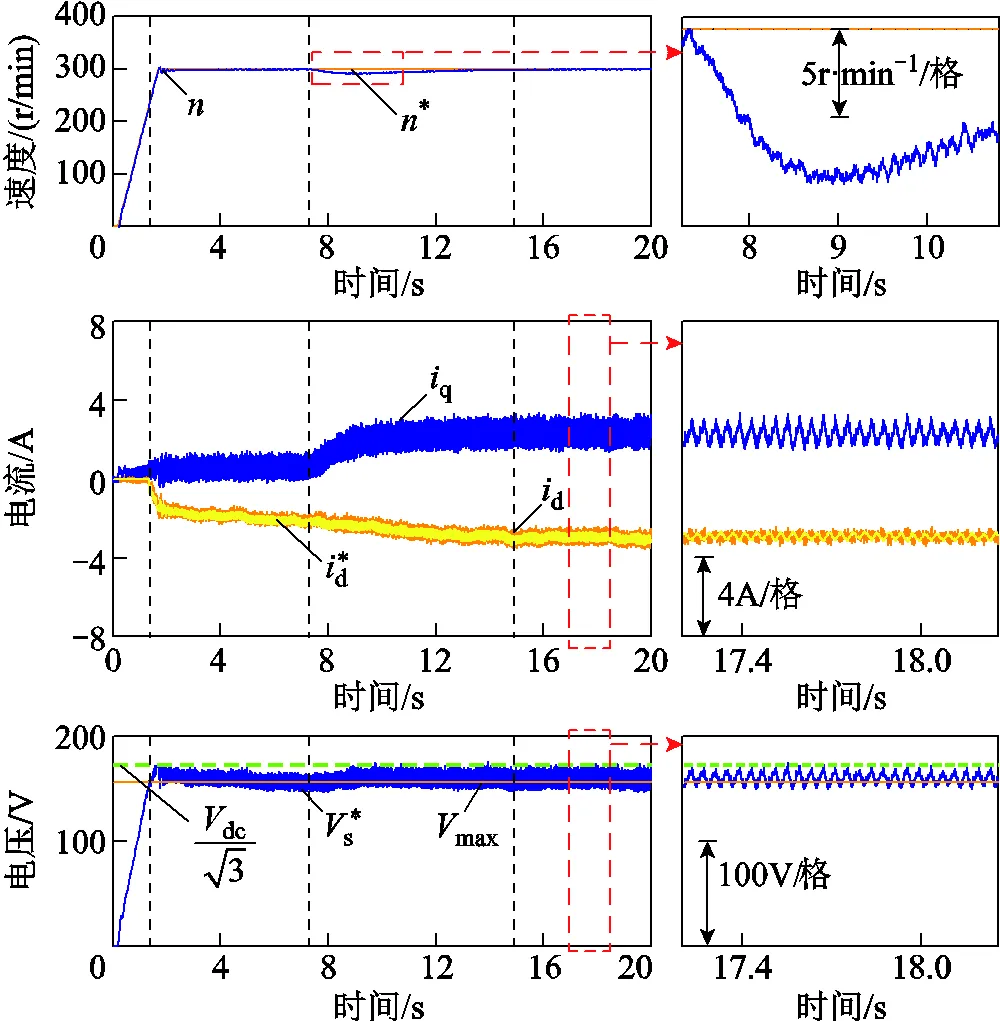
图14 ADRC方法突加负载实验波形

图13与图14说明纯积分器方法可以在空载情况下运行在弱磁区间，但稳态加载后系统波动增加，超过最大限制并逐渐失控。ADRC方法在转速和定子电压动态响应上均优于纯积分器方法，并且加载后仍然能保持稳定运行。

纯积分器方法在较深的弱磁深度下带载起动与突然加载后均失控是由于纯积分器方法d轴电流绝对值偏大，稳态工作点偏左，在较深的弱磁深度下系统阻尼因子下降[11]、相位裕度变小[13]，导致系统失控。带载后系统电流、定子电压波动有所增加，使系统失控加剧。而ADRC可以通过ESO较好地观测并补偿系统中的各种扰动，d轴电流绝对值偏小，稳态工作点偏右，系统能更平稳地运行在弱磁区域，避免失控。

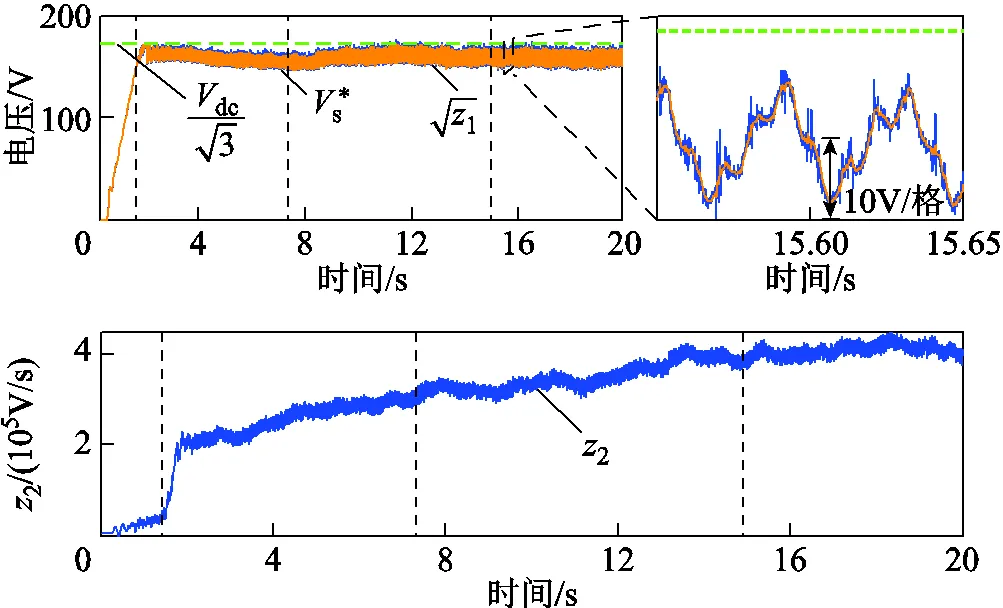
图15 ESO观测波形

4 结论

本文提出了一种基于自抗扰控制技术的永磁同步电机电压反馈弱磁控制方法，给出了参数整定的原则并利用描述函数法证明了系统的稳定性。实验证明，本文设计的自抗扰控制器可对系统扰动进行较好的观测并补偿，实现了在空载起动、带载起动、突加负载三种工况下的稳定运行，保证了实际应用中的可靠性。与基于纯积分器的传统电压反馈弱磁控制方法相比，基于自抗扰控制的方法带载能力更强，稳定性更好。

附 录

式（22）系数为

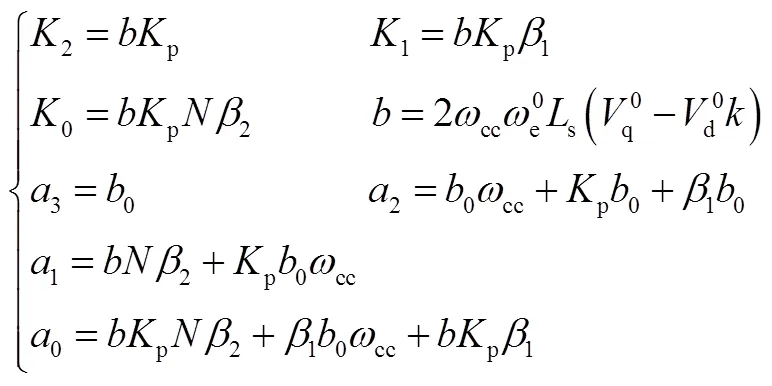
前向通道和各回路传递函数为

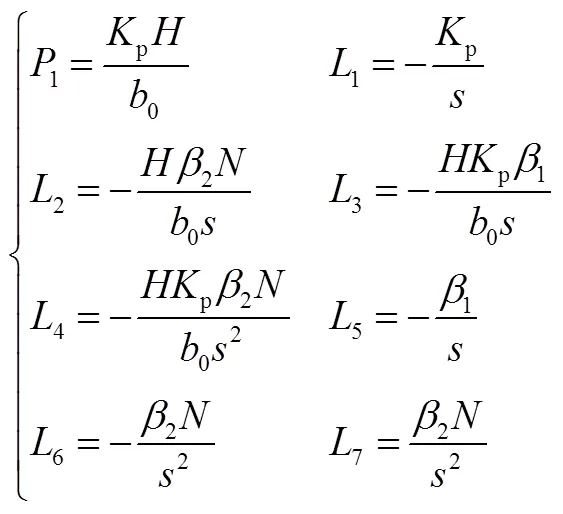
式（23）系数为

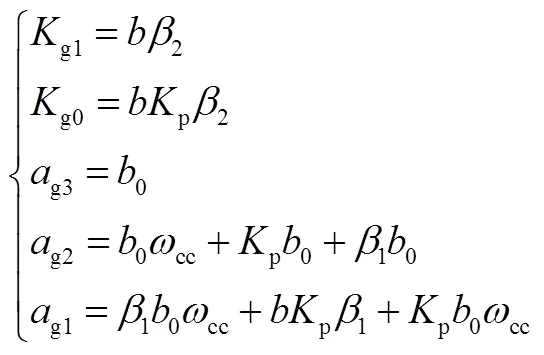
[1] 李雪, 迟颂, 刘聪, 等. 基于虚拟电阻的永磁同步电机单电流调节器弱磁控制[J]. 电工技术学报, 2020, 35(5): 1046-1054.

Li Xue, Chi Song, Liu Cong, et al. Flux-weakening control with single current regulator of permanent magnet synchronous motor based on virtual resistor[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 1046-1054.

[2] 莫为, 汪梅, 莫会成. 不同转子结构对永磁交流伺服电机弱磁特性影响[J]. 电工技术学报, 2018, 33(增刊1): 89-98.

Mo Wei, Wang Mei, Mo Huicheng. Influence of different rotor structure on flux-weakening properties of permanent magnet AC servo motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 89-98.

[3] 吴荒原, 王双红, 辜承林, 等. 内嵌式永磁同步电机改进型解耦控制[J]. 电工技术学报, 2015, 30(1): 30-37.

Wu Huangyuan, Wang Shuanghong, Gu Chenglin, et al. An improved decoupling control strategy for the IPMSMS[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 30-37.

[4] Yang Nanfang, Luo Guangzhao, Liu Weiguo, et al. Interior permanent magnet synchronous motor control for electric vehicle using look-up table[C]//Power Electronics & Motion Control Conference, Harbin, China, 2012: 1015-1019.

[5] Chen Yuzheng, Huang Xiaoyan, Wang Jun, et al. Improved flux-weakening control of IPMSMs based on torque feedforward technique[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10970-10978.

[6] Kwon T S, Sul S K. Novel anti-windup of a current regulator of a surface-mounted permanent-magnet motor for flux-weakening control[C]//Fortieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2005: 1813-1819.

[7] Qiao Mingzhong, Peng Wei, Zhu Peng, et al. Research on leading angle flux-weakening control strategy of permanent magnet synchronous motor based on over-modulation algorithm[C]//2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 2021: 1035-1041.

[8] Nalepa R, Orlowska-Kowalska T. Optimum trajectory control of the current vector of a nonsalient-pole PMSM in the field-weakening region[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7): 2867-2876.

[9] 康劲松, 蒋飞, 钟再敏, 等. 电动汽车用永磁同步电机弱磁控制策略综述[J]. 电源学报, 2017, 15(1): 15-22.

Kang Jinsong, Jiang Fei, Zhong Zaimin, et al. Overviews of flux weakening control schemes with permanent magnet synchronous motor used in electric vehicles[J]. Journal of Power Supply, 2017, 15(1): 15-22.

[10] Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[11] Wang C, Zhu Z Q, Zhan Hanlin. Adaptive voltage feedback controllers on the non-salient permanent magnet synchronous machine[C]//2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 2018: 1374-1380.

[12] Wang Chao, Zhu Z Q. Fuzzy logic speed control of permanent magnet synchronous machine and feedback voltage ripple reduction in flux-weakening operation region[J]. IEEE Transactions on Industry Applications, 2020, 56(2): 1505-1517.

[13] Bolognani S, Calligaro S, Petrella R. Adaptive flux-weakening controller for interior permanent magnet synchronous motor drives[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 236-248.

[14] Bedetti N, Calligaro S, Petrella R. Analytical design and autotuning of adaptive flux-weakening voltage regulation loop in IPMSM drives with accurate torque regulation[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 301-313.

[15] Jacob J, Calligaro S, Bottesi O, et al. Design criteria for flux-weakening control bandwidth and voltage margin in IPMSM drives considering transient conditions[C]//2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, 2019: 5667-5674.

[16] 盖江涛, 黄守道, 黄庆, 等. 基于负载观测的永磁电机驱动系统自抗扰控制[J]. 电工技术学报, 2016, 31(18): 29-36.

Gai Jiangtao, Huang Shoudao, Huang Qing, et al. Active-disturbance rejection controller for permanent magnet motor drive system control based on load observer[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 29-36.

[17] Zuo Yuefei, Mei Jie, Jiang Chaoqiang, et al. Linear active disturbance rejection controllers for PMSM speed regulation system considering the speed filter[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14579-14592.

[18] Lin Ping, Wu Zhen, Liu Kunzhi, et al. A class of linear–nonlinear switching active disturbance rejection speed and current controllers for PMSM[J]. IEEE Transactions on Power Electronics, 2021, 36(12): 14366-14382.

[19] 刘春强, 骆光照, 涂文聪, 等. 基于自抗扰控制的双环伺服系统[J]. 中国电机工程学报, 2017, 37(23): 7032-7039, 7095.

Liu Chunqiang, Luo Guangzhao, Tu Wencong, et al. Servo systems with double closed-loops based on active disturbance rejection controllers[J]. Proceedings of the CSEE, 2017, 37(23): 7032-7039, 7095.

[20] 杜博超, 韩守亮, 张超, 等. 基于自抗扰控制器的内置式永磁同步电机无位置传感器控制[J]. 电工技术学报, 2017, 32(3): 105-112.

Du Bochao, Han Shouliang, Zhang Chao, et al. Sensorless control of interior permanent magnet synchronous motor based on active disturbance rejection controller[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 105-112.

[21] 孙斌, 王海霞, 苏涛, 等. 永磁同步电机调速系统非线性自抗扰控制器设计与参数整定[J]. 中国电机工程学报, 2020, 40(20): 6715-6726.

Sun Bin, Wang Haixia, Su Tao, et al. Nonlinear active disturbance rejection controller design and tuning for permanent magnet synchronous motor speed control system[J]. Proceedings of the CSEE, 2020, 40(20): 6715-6726.

[22] 朱斌. 自抗扰控制入门[M]. 北京: 北京航空航天大学出版社, 2017.

[23] 黄一, 韩京清. 非线性连续二阶扩张状态观测器的分析与设计[J]. 科学通报, 2000, 45(13): 1373-1379.

Huang Yi, Han Jingqing. Analysis and design of nonlinear second-order extended state observer[J]. Chinese Science Bulletin, 2000, 45(13): 1373-1379.

[24] 韩京清, 张荣. 二阶扩张状态观测器的误差分析[J]. 系统科学与数学, 1999, 19(4): 465-471.

Han Jingqing, Zhang Rong. Error analysis of the second order ESO[J]. Journal of Systems Science and Mathematical Sciences, 1999, 19(4): 465-471.

[25] Wu Dan, Chen Ken. Frequency-domain analysis of nonlinear active disturbance rejection control via the describing function method[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3906-3914.

Flux Weakening Control Strategy of Permanent Magnet Synchronous Motor Based on Active Disturbance Rejection Control

Li Siyi Su Jianyong Yang Guijie

（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

In this paper, a voltage feedback flux weakening control method based on active disturbance rejection control(ADRC) is proposed to solve the problem that the voltage feedback flux weakening control using pure integrator will oscillate or even lose control when the flux weakening degree is deep. By establishing the small signal time domain model of the voltage loop, the active disturbance rejection voltage controller is designed, the selection principle of the controller parameters is given, and the stability is analyzed by using the describing function method. This method does not rely on the accurate model of the controlled object, and has strong robustness. It can effectively observe and compensate the nonlinear and other disturbance factors in the system, and effectively deal with linear and nonlinear control objects. The experimental results show that compared with the pure integrator method, the proposed method has stronger load capacity and better stability when the flux weakening depth is deeper.

Permanent magnet synchronous motor, flux weakening, active disturbance rejection control, describing function method

10.19595/j.cnki.1000-6753.tces.211129

TM341

2021-07-23

2021-12-15

李思毅 男，1998年生，硕士研究生，研究方向为永磁同步电机弱磁控制。E-mail：lisiyihit@163.com

苏健勇 男，1979年生，副教授，硕士生导师，研究方向为永磁同步电机驱动与控制技术及模型预测控制等。E-mail：hitsujy@126.com（通信作者）

（编辑 赫蕾）