考虑工人学习效应的双资源约束柔性车间调度*
侯天天,张守京,杜昊天
(西安工程大学机电工程学院,西安 710600)
0 引言
车间调度问题是生产调度领域广受学者关注的问题之一,优化调度方案能一定程度提高生产效率,降低成本。在实际生产中,工人资源也是直接影响车间产能的重要因素之一[1]。由于人力成本逐年递增,工人操作机器的技能受限或存在差异,合理工人分配资源十分必要。双资源约束柔性车间调度问题(dual-resource constrained flexible job shop scheduling problem,DRCFJSP)就是在经典柔性车间调度问题(FJSP)基础上,增加了工人选择的子问题,求解空间和难度大幅增加,是更复杂的NP-Hard问题,已有众多学者针对该问题开展了广泛研究。
OBIMUYIW等[2]考虑有限数量的熟练安装工人,建立DRCFJSP的MILP模型,并采用遗传算法进行求解;GONG等[3]提出考虑工人灵活性的柔性车间调度模型(FJSPW),采用混合人工蜂群算法(HABCA)进行求解,并通过实验证明该算法求解FJSPW问题的优越性;肖倩乔等[4]考虑工人学习因素对产能的影响,构建基于学习曲线的人机资源配置模型,有效解决了多目标双重资源配置;胡金昌等[5]为解决单人单工序多机的车间调度问题,根据学习效应计算实际安装时间,构造迭代多目标遗传算法(IMOGA)进行求解;PENG等[6]采用混合离散多目标帝国竞争算法(HDMICA),求解受工件运输时间和学习效果约束的多目标柔性车间调度问题模型;曹磊等[7]为解决异质性全技能工人与机器的配置问题,构建基于车间层面的多目标模型,提出一种双层编码的变邻域杂草优化算法进行求解。
上述研究虽有考虑到工人的学习因素,但很少有学者将其量化,且没有考虑工人技能柔性程度的影响。基于此,本文提出考虑工人技能柔性度的学习效应曲线,构建以最小化完工时间、加工成本和环境指标为优化目标的DRCFJSP模型。为更好地求解该问题,融合MOPSO和NSGA-Ⅱ设计非支配排序混合遗传算法(non-dominated sorting hybrid genetic algorithm,NSHGA-Ⅱ),并通过实例仿真验证了该算法的有效性和优越性。
1 问题描述及数学模型
1.1 问题描述
考虑学习效应的DRCFJSP可描述为:某调度周期内,w名操作工人(W={W1,W2,…,Ww})操作m台加工机器(M={M1,M2,…,Mm})加工n个工件(J={J1,J2,…,Jn});工件i有ni个待加工工序(Oi={Oi1,Oi2,…,Oini}),工序之间具有优先级约束;不同机器和工人的技能柔性程度不同,工人的技能水平受学习能力影响。在求解该问题时需考虑工序排序、机器选择和工人选择3个约束,以及工人实际操作时间动态变化的情况。假设条件如下:
(1)工件、机器及工人在零时刻均空闲可用;
(2)加工过程稳定运行,不允许中断;
(3)同一时刻,任一机器至多加工一个工序,任一工序至多由一台机器加工;
(4)同一时刻,任一机器至多由一个工人操作,任一工人至多操作一台机器;
(5)工人须在一个工序加工完成后才可转移;
(6)运输、刀具更换等时间考虑在加工时间内。
1.2 考虑工人技能柔性度的学习效应曲线
学习效应(learning effect)是指工人在连续的生产周期中,通过不断重复地做同一个工作或类似工作,其自身知识经验得以积累,操作的熟练程度得到提升,从而减少操作时间或者成本的现象。由于人的异质性,每个工人的培训效果不同,技术水平存在差异,从而影响实际加工时间。因此,研究学习效应对生产调度的影响十分必要,本文采用基于对数模型的DeJong学习曲线模型[8],如式(1)所示。
(1)

然而,对于一些机器操作难度大、人机协作要求高的行业,为保证工人良好的工作状态,降低工人离岗的负面影响,人机比率可能大于1;此外,不同程度交叉培训的工人具有技能柔性差异,这些情况下采用人机比率表示F不再适用。由于工人作业常为同种任务类型,其掌握技能数量也会影响操作熟练度,为此引入工人技能柔性度表示F。首先,为量化工人技能柔性度[10],定义人机关系矩阵PM=(PMsk)w×m,其中PMsk∈{1,0}分别表示工人s能否操作机器k,工人技能柔性度FI如式(2)所示。
(2)
式中,FI∈[0,1],FI越大,说明工人对机器的技能柔性越高,反之柔性越低。对于考虑工人技能部分柔性的情况,FI∈(0,1)。

(3)
αsk=lglsk/lg2
(4)

1.3 多目标DRCFJSP模型

目标函数为最小化完工时间(T)、加工成本(C)和环境指标(EI)(考虑能耗、废屑和噪声),如式(5)~式(7)所示。

(5)
(6)

(7)
式中,在对计算环境评价的3个指标时,由于数据单位的不同,需对其去量纲处理,计算公式如式(8)所示,X′表示处理后的数据结果。
(8)
在求解DRCFJSP时,还需满足以下约束:
(9)
(10)
(11)
[Sijks,Fijks]∩[Si′j′ks′,Fi′j′ks′]=∅
(12)
式中,∀i,i′∈{1,2,…,n};∀j,j′∈{1,2,…,ni};∀k∈{1,2,…,m};∀s∈{1,2,…,w},i≠i′;j≠j′。式(9)表示同一时刻任一工件的任一工序只能选择一台机器和一个工人进行加工;式(10)表示同一工件的工序优先级约束;式(11)表示加工过程不可中断;式(12)表示两道工序在一台机器上的加工时间不可交叉。
2 改进NSHGA-Ⅱ求解多目标DRCFJSP模型
2.1 求解流程
多目标DRCFJSP约束复杂、求解难度大,为避免求解过程无效解的产生,采用工序编码,并设计解码策略获得可行解;NSHGA-Ⅱ算法将NSGA-Ⅱ和MOPSO相结合,具有高效的全局搜索效率和精确率;为避免算法陷入局部最优,在目标迭代停滞时执行邻域搜索。求解流程图如图1所示,步骤如下:
步骤1:设置算法参数,迭代次数maxGen,进化最大停滞代数N,种群规模popsize等;
步骤2:初始化种群F(t):随机生成工序编码,通过解码获得对应机器、工人序列及可行解;
步骤3:计算种群F(t)个体适应度,进行快速非支配排序;算法迭代开始,令t=1;
步骤4:粒子更新:①更新权重;②找出最优个体;③粒子更新;④计算新种群P(t)个体适应度;
步骤5:遗传操作:①竞标赛选择;②交叉变异操作;③计算新种群G(t)个体适应度;
步骤6:合并子父代种群P(t)、G(t)和F(t),删除重复个体,若剩余个体数量小于popsize,则转到步骤4,否则进行快速非支配排序,选择种群规模大小的新种群;
步骤7:若种群进化停滞代数达到N,进行邻域搜索,否则执行步骤8;
步骤8:令t=t+1,得到新一代种群F(t),若t 步骤9:熵值法选出最优解,绘制Pareto解集图,最优调度方案甘特图,算法迭代图。 图1 NSHGA-Ⅱ算法求解多目标DRCFJSP流程图 为简化算法流程,保证编码的有效性,选择基于工序的编码方式,以分别有3、2、2道工序的3个工件为例,示意图如图2所示。 图2 工序编码示意图 为选择合适的机器和工人,以完工时间为导向,设计一种考虑工人学习效应的贪婪解码策略:为各工序选择完工时间最小的机器和工人,以确定工序的加工顺序、起始加工时间等,生成可行调度方案。对于待加工工序Oij,可加工时刻为Sij(Sij=Ti(j-1)),解码步骤如下: 步骤1:遍历可加工工序Oij的机器集中各机器的加工任务,任一机器k的可用时刻记为Ak(即机器k上一任务完工时间);若Sij≥Ak,则Ak=Sij,选择完工时间(即Ak与tijk之和)最小的机器,记为集合kij; 步骤4:更新Ak=As=Tij,若j=ni,则Ti=Tij,否则Si(j+1)=Tij。 2.3.1 粒子更新 粒子群算法是模拟鸟类捕食行为的一种群体智能算法[12],每个粒子表示一个潜在解,粒子根据个体最优和全局最优位置指导自己速度和位置的更新,如式(13)~式(14)所示。 (13) (14) 式(13)中w是平衡算法搜索能力的重要参数,采用指数形式的时变权重如式(15)所示。 (15) 式中,wt为第t代的权重值;wmax和wmin分别为权重上下限;t为种群当前迭代次数;maxGen为最大迭代次数。 2.3.2 遗传操作 选择操作:采用三元锦标赛的方法,将非支配排序等级和拥挤度作为适应度的判断值,扩大精英个体遗传子代的概率;交叉操作:针对工序编码,采用JBX[13]和PBX[14]两种单一交叉算子相结合的方式,各按1/2的概率交替选择;变异操作:针对工序编码,采用任意三点基因互换的方式和两段基因分别倒序的方式,示意图如图3所示。 图3 变异操作示意图 为避免固定的交叉变异概率造成算法收敛波动大,采用动态变化的交叉变异率,第t代交叉或变异率如式(16)所示。 pxt=pxmax-(pxmax-pxmin)×t/maxGen (16) 式中,pxmax={pcmax,pumax};pxmin={pcmin,pumin}。 由于遗传算法和粒子群算法在局部搜索上均存在不足,为丰富种群多样性提升解集质量,针对任意两点基因构造4种邻域搜索算子:两点互换、两点间倒置、插入和邻位互换,在搜索时只接受优于原个体的新解。以图2的工序编码为例,随机选择两个基因位2和5,其4种邻域结构如图4所示。 图4 邻域搜索算子示意图 以某车间调度实例数据为基准进行仿真实验。车间内共有6台机器(M1~M6)和7个负责机器上下料的工人(W1~W7),加工有若干工序的6个工件(J1~J6)。工序与机器、工人与机器的加工关系信息分别如表1和表2所示,工人和机器的单位成本如表3所示,污染指标中的能耗、噪音、废屑数据参考文献[13]的规律随机生成。通过参考文献[16]与正交试验确定算法参数设置:popsize=200,maxGen=200,c1=c2=2,wmax=0.95,wmin=0.5,pcmax=0.8,pcmin=0.4,pumax=0.2,pumin=0.1。 表1 工序加工时间表 续表 表2 工人与机器加工关系表(上下料时间/初始能力/学习率) 表3 机器和工人单位时间成本 首先,采用NSHGA-Ⅱ算法求解不同人机比例下的最优调度方案,如图5~图7所示,分别为工人数为5、6、7名时的最优方案甘特图(实线框为工序的机器加工时长,虚线框为工人作业时长),验证可知所提模型的有效性。 图5 5名工人的最优调度方案甘特图 图6 6名工人的最优调度方案甘特图 图7 7名工人的最优调度方案甘特图 以6名工人为例分析算法性能,图8为NSHGA-Ⅱ、NSGA-Ⅱ和MOPSO三种算法Pareto解集的分布情况。 图8 Pareto解集分布图 图中NSHGA-Ⅱ的解集更靠近理想原点;此外,针对Pareto解集采用3种评价指标:①基数:解的数量(Q);②收敛性:中值距离(MID)[6];③多样性:空间分布(spacing)。表4为3种算法的最优解目标值、Pareto解集目标均值和评价指标的结果;通过对比可知,NSHGA-Ⅱ的最优解和解集均值在3个目标上均占优于其他两种算法,而且解的数量最多,MID和Spacing的值最小,表明解集的收敛性和多样性最佳。 表4 3种算法求得的最优解的多目标值 图9~图11为3种算法Pareto解集的3个目标均值迭代情况。 图9 Pareto解集平均完工时间迭代图 图10 Pareto解集平均环境指标迭代图 图11 Pareto解集平均加工成本迭代图 从收敛情况看, NSHGA-Ⅱ算法的寻优速度均明显优于其他两种算法;在寻优能力上,MOPSO算法和NSGA-Ⅱ算法容易早熟收敛,而NSHGA-Ⅱ算法能跳出局部最优。 本文研究了考虑工人学习效应的多目标DRCFJSP,引入工人技能柔性度构建数学模型,并提出一种NSHGA-Ⅱ算法进行求解。为保证迭代过程中解的可行性,针对工序编码设计基于完工时间的贪婪解码策略;NSHGA-Ⅱ算法结合MOPSO和NSGA-Ⅱ的优良性能,提高算法全局开发能力;构造的四种邻域算子提高算法局部搜索能力;采用熵值法客观选择最优调度方案。最后通过实例仿真,验证了模型的有效性,将NSHGA-Ⅱ、NSGA-Ⅱ和MOPSO的结果对比可知,NSHGA-Ⅱ的解集质量和寻优收敛情况均明显优于其他两种算法,证明了所提算法求解该类问题的可行性与优越性。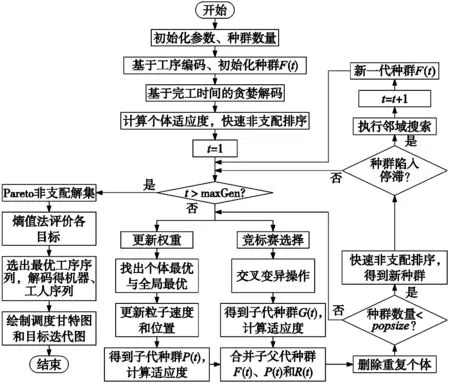
2.2 编码与解码



2.3 全局搜索



2.4 邻域搜索

2.5 熵值法评价策略

3 实例仿真分析











4 结束语

