面向球的自驱动关节臂测量机最佳测量区*

杨洪涛，陈 贺，沈 梅

(安徽理工大学a.机械工程学院；b.矿山智能装备与技术安徽省重点实验室，淮南 232001)

0 引言

随着我国工业智能制造技术的快速发展与更新迭代，对工业生产线产品的在线检测装备与技术提出了更高的要求[1-2]。自驱动关节臂式坐标测量机是一种非正交柔性坐标测量设备，利用角度基准实现其工作空间内的工件形貌检测及其几何尺寸测量，具有高通用性、高精度、高效率等特点。当待测工件置于空间不同区域内时，自驱动关节臂坐标测量机以不同的测量姿态对工件进行测量，导致测量机产生不同的测量误差，且上述误差在测量机的测量空间范围内连续性变化并呈一定分布规律[3-4]。因此，在关节臂坐标测量机整个测量空间范围内，必存在一个最佳测量区域，将待测工件置于该区域内时，测量机测得的工件几何尺寸误差最小。

针对上述问题，国内外学者对关节臂式坐标测量机的最佳测量区域确定方法进行了深入研究。WERNER[5]根据其研究的ScanMax坐标测量机的结构和误差分布，建立了测量机的测量方程和误差方程，并对二维平面上的最佳测量区进行了研究。通过泛函网络理论和v-SVMRBF核函数，构建柔性坐标测量机新型点误差模型和空间误差分布模型，并采用偏微分方法对误差进行建模，对柔性坐标测量机的测量空间的求解问题，采用Monte Carlo理论进行求解[6]。通过确定柔性坐标测量机的最佳测量区，从而提高对工件的测量精度。WANG等[7]通过基于密度的带噪声应用空间聚类(DBSCAN)的子测量区域划分和合并方法，验证了可以在精度区域进行测量来提高测量精度。胡毅等[8]通过研究整个测量空间，发现不同测量区存在差异，即存在误差较大的测量区域和误差较小的最佳测量区域。胡毅、江超等[9-10]基于关节臂测量机各圆编码器误差特性，通过将测量空间等间隔分割成若干个小立方区域，采用改进的蚁群算法求出各个小区域的最大测量误差，得到最佳测量区。江超等[10]利用关节式坐标测量机对空间某一点进行多种姿态测量，得出6个圆编码器测角误差组合在不同姿态下是不同的。

由上述分析可知，目前国内外学者对关节臂测量机的最佳测量区研究主要针对手动式关节臂坐标测量机，然而自驱动关节臂坐标测量机的旋转关节内部引入驱动模块和自动测量系统，其机械结构和控制系统与手动式测量机不同，静态与动态误差来源更广泛，且各项误差之间的耦合关系更复杂，导致其在不同测量区域的工件测量误差分布与手动式测量机亦存在差异。因此，需对自驱动关节臂坐标测量机面向对象的最佳测量区进行研究。此外，自驱动关节臂坐标测量机测量的工件几何特征包括空间点坐标、长度、平面以及球等复杂曲面，且测量机测量的直接结果为点的空间坐标，长度、平面、曲面等几何特征结果则是以上述点坐标进行变换求解，故基于自驱动关节臂坐标测量机的曲面测量最复杂。

本文基于课题组设计研制的自驱动关节臂坐标测量机结构原理，采用MDH参数法建立其理想测量模型[11]，系统性分析静态、动态误差来源，提出面向球的自驱动关节臂坐标测量机的最佳测量区确定方法，通过单位四元数球面线性插值算法求解测量机的不同测量姿态，利用测量机样机搭建并开展面向球的最佳测量区测试实验，由此确定自驱动关节臂坐标测量机面向球的最佳测量区域，以助于提高其自动定位与测量精度，为工件几何特征测量策略提供理论参考。

1 测量机结构原理与误差源分析

1.1 测量机结构原理与测量模型

自驱动关节臂坐标测量机是一种新型非正交式柔性坐标测量设备，如图1所示，其组成部件包括：基座、6个旋转关节、关节臂连杆以及触发式测头等结构。自驱动关节臂坐标测量机通过在6个旋转关节内部引入一体化关节模组，实现设备的自驱动控制和在线自动测量。

图1 自驱动关节臂坐标测量机整体结构

自驱动关节臂坐标测量机在测量工件时，根据测量机测头起点与工件目标点的坐标值进行规划轨迹，采用逆运动学法求解关节所需转动的理论角度，通过驱动系统控制各关节转动相应角度，实现测量机的自驱动定位测量。自驱动关节臂坐标测量机的测量过程分为变速靠近和匀速触测[12]，变速靠近采用轨迹规划控制末端测头以加速-匀速-测目标点。当测头触测目标点时，上位机接收测头信号并记录关节转动实际角度，将实际角度和结构参数代入测量模型，计算出测头到达目标点时的实际空间坐标，完成测量任务。

为了求解自驱动关节臂坐标测量触测目标点的空间坐标，基于测量机串联结构特点，采用改进的denavit-hartenberg(MDH)参数法[13]建立其理想测量模型。分别在测量机的基座、测头、关节适当位置建立局部坐标，图2为运动传递原理图，其中坐标系{x0,y0,z0}为固定坐标系，{x1,y1,z1}～{x6,y6,z6}为关节坐标系，{x7,y7,z7}为测头坐标系。

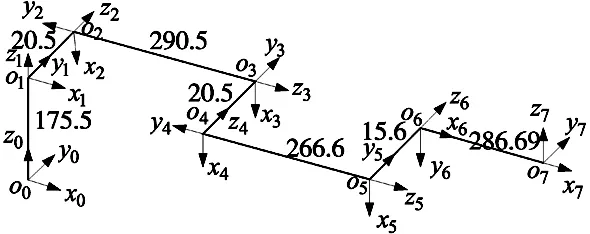
图2 AACMM运动传递原理图

相邻坐标系{Xi-1,Yi-1,Zi-1}和{Xi,Yi,Zi}之间经过2次旋转和2次平移实现坐标系变换，其齐次变换矩阵如式(1)所示[14]。

(1)

式中，θi为关节i转角值；αi-1为关节i-1和关节i之间的杆件扭转角；ai为对应关节长度；di为相邻关节间的杆件偏置长度。

根据MDH参数法得到如式(2)所示的测量机的理想测量模型。

(2)

式中，P=[xyz1]为测头在固定坐标系中的空间坐标。表1为理想测量模型的结构参数值。

表1 自驱动关节臂坐标测量机理想测量模型结构参数

1.2 测量机误差来源分析

当自驱动关节臂坐标测量机对工件进行测量时，零件的制造安装、关节连杆的柔性变形、测量的运动参数以及工作环境等因素均会影响测量机的自动定位与测量精度。相较于手动式测量机，自驱动关节臂坐标测量机旋转关节内部引入一体化关节模组，其误差来源更广泛。本节根据自驱动关节臂坐标测量机的结构原理，对其误差来源进行详细分析。

1.2.1静态误差分析

(1)零件制造误差。测量机零件的加工工艺、加工环境等因素将影响零件的形位制造精度。如关节臂连杆的杆长尺寸制造误差将导致测量模型中的连杆长度和关节偏置等结构参数存在误差，连杆安装面平行度制造误差、连杆轴线垂直度制造误差将导致关节转角和扭转角等结构参数存在误差。

(2)零部件安装误差。利用加工零部件进行测量机整机装配时，基座与工作台之间、各零部件(含选型部件和加工零件)之间存在的装配误差将使得测量模型中的连杆长度、关节偏置、关节转角以及关节扭转角等结构参数存在误差。

(3)连杆静态弯曲变形误差。测量机的关节臂连杆在静态时会因自身重力及其所承负载共同作用下发生静态弯曲变形，由此产生的杆件弯曲转角和挠度将带来连杆长度、关节偏置以及关节扭转等参数误差。

(4)关节静态扭转变形误差。测量机6个旋转关节均采用一体化关节模组，当测量机为静态时，其各关节模组因其末端连接不同的负载而产生不同的静态扭转变形，导致测量模型中的关节转角参数存在误差，影响测量机测头的定位精度。

1.2.2 动态误差分析

自驱动关节臂坐标测量机的动态误差项中，其零件制造误差和零部件安装误差与静态误差项中的相同。其中，相邻零部件之间的安装精度可能会随着测量机的运动而发生微小改变，导致零件安装误差存在动态变化的随机性。同时，测量机的动态误差项还包括以下内容：

(1)连杆动态弯曲变形误差。当测量机运动测量时，关节臂各段连杆末端所承的负载力矩与连杆空间瞬时姿态及其运动参数有关。当关节臂连杆的空间瞬时姿态不同时，其因负载力矩产生的动态弯曲变形也不同，继而导致关节臂连杆长度、关节扭转角等结构参数产生动态误差。

(2)关节动态扭转变形误差。当测量机运动测量时，其旋转关节末端所承的负载力矩与关节负载的空间瞬时姿态和关节转动加速度有关。当旋转关节的空间瞬时姿态不同时，其因负载力矩产生的动态扭转变形也不同，继而导致关节转角参数存在动态误差。

(3)关节模组驱动测角误差。自驱动关节臂坐标测量机关节内部引入一体化关节模组，当关节模组转动时，该类型关节模组内部的谐波减速器、伺服电机、磁编码器将分别产生谐波减速器转角误差、伺服电机转角误差、磁编码器测角误差，上述误差将导致测量模型中的实际关节转角存在动态误差，影响测量机的动态定位精度。

此外，由电机驱动所增加的热源、环境温度导致的热变形误差、结构参数标定误差和控制系统响应导致的控制系统也会影响自驱动关节臂坐标测量机的动态定位精度。

由上述误差溯源分析可知，自驱动关节臂坐标测量机的自动定位与测量精度受零部件制造安装、关节杆件动态变形、运动测量参数以及工作环境等多种因素影响。其中，当待测工件置于不同测量区域时，测量机的测量姿态不同，其关节杆件的动态柔性变形也不同，最终导致测量机测得的工件尺寸误差存在差异。因此，在自驱动关节臂坐标测量机整个工作空间范围内，必然会存在一个测量区域，使得工件几何特征的测量误差最小，则称该区域为自驱动关节臂坐标测量机的“最佳测量区”。此外，自驱动关节臂坐标测量机在对不同待测对象进行测量时，因几何形状和测量路径不同，导致最终测得的工件几何特征测量误差分布规律同样存在差异。其中，相较于点、直线、平面等简单工件几何特征，当自驱动关节臂坐标测量机的测量对象为曲面时，其测量过程与几何特征结果计算最复杂。为了确保测量机面向不同工件几何特征测量时，最佳测量区存在的可靠性，本文以最复杂的曲面测量为研究对象，开展面向球的自驱动关节臂坐标测量机最佳测量区确定方法研究。

1.3 面向标准球的最佳测量区确定方法

为了研究面向球的自驱动关节臂坐标测量机的最佳测量区，本文以标准球半径为测量对象，确定测量机面向球的最佳测量区方法。将标准球固定于测量机的某一空间位置，通过改变测量机关节模组不同的角度组合，控制测量机以不同的姿态触测球表面不同的4个点，利用4点法[15]求解得到球的不同测量半径误差[16]。通过比较上述误差值，确定球位于该空间位置时的最大半径测量误差δR[max]i。其中，4点法求解球心坐标和球半径的原理如图3所示。

图3 4点法求解空间球面方程原理

根据测量机测得的球表面4个点空间坐标Pi(xi,yi,zi)，i=1～4，设空间球面方程如式(3)所示，其中球心坐标为Q(m,n,k)，半径为R。

(x-a)2+(y-b)2+(z-c)2=r2

(3)

对式(3)展开并整理得到：

-2xa-2yb-2zc+1*(a2+b2+c2-r2)=-x2-y2-z2

(4)

将4个点空间坐标Pi(xi,yi,zi)，i=1～4，代入式(4)得到4个线性方程组：

(5)

(6)

式(4)写为矩阵形式为式(6)所示，由此则将非线性空间球面方程转化为线性问题，利用最小二乘法求解出式(6)中的m，n，k，R。

在此基础上，改变标准球在测量机工作空间中的固定位置，重复上述球半径测量操作，最终得到一组球固定于自驱动关节臂坐标测量机工作空间中不同位置处的最大半径测量误差δR[max]1,δR[max]2,…,δR[max]n-1,δR[max]n，n为球在测量机工作空间中的固定位置数目。通过数据对比得到球的最大半径测量误差值最小的测量区域，该区域即为自驱动关节臂坐标测量机面向球的最佳测量区。

2 自驱动坐标测量机不同测量姿态求解

根据前文面向球的自驱动关节臂坐标测量机最佳测量区确定方法可知，控制测量机关节模组以不同角度组合去测量同一测量位置处的标准球半径，求解测量机在不同姿态下测得的球半径测量误差是研究其最佳测量区的关键一步，因此，本节针对测量机的不同测量姿态求解方法作进一步研究。

2.1 基于单位四元数球面线性插值算法

为了求解测量机测量空间采样点的n(n值取决于起始测量姿态与终止测量姿态中间的插补步长)种不同测量姿态，定义测量机测量空间采样点的第1个测量姿态和第n个测量姿态，通过对上述两种测量姿态之间进行插值[17]，求解得到中间n-2个测量姿态。目前，通常采用四元数插值算法，该算法包括正规化线性插值(Nlerp)、球面线性插值(Slerp)以及球面四边形插值(Squad)等[16]。通过对比三种插值方法特点[18]，并综合考虑关节模组转动角速度的均匀性[16]，本文采用单位四元数球面线性插值算法[18]，求解测量机的不同测量姿态。单位四元数球面线性插值原理如图4a所示，通过一般线性插值公式：vt=k1v1+k2v2。以v1和v2之间插值变换为例，其几何关系如图4b所示。

(a) 角度线性插值 (b) 向量几何关系

图4b中，k2v2//v2，由ΔACB和ΔOAB的几何关系可知：

sin(α1t)=x1/vt

(7)

sin(α1)=x1/k2v2

(8)

因v1、v2、vt为单位向量，故sin(δ1t)=x1，sin(δ1)=x1/k2，代入式(7)和式(8)并联立计算可得：

k2=sin(δ1t)/sin(δ1)

(9)

同理，图4b中ΔAED和ΔOAD的几何关系如式(10)和式(11)所示，联立计算得出k2。

sin((1-t)δ1)=x2/vt=x2

(10)

sin(δ1)=x2/k1v1=x2/k1

(11)

k1=sin((1-t)δ1)/sin(δ1)

(12)

将式(12)和式(9)代入一般线性插值公式vt=k1v1+k2v2，得到中间向量vt为：

(13)

利用插值变换原理及计算模型，通过单位四元数球面线性插值法，求解n种不同测量姿态下测量机的测量采样点，插值模型最终即为：

(14)

根据上述单位四元数球面线性插值算法，求解出测量机测量某一空间位置处的球的不同测量姿态，为求解测量机以不同姿态测量同一位置处的球半径测量误差，并找出该位置处的球半径最大测量误差提供重要基础。之后，改变球的空间位置，通过比较不同位置的球半径最大测量误差，可以得出自驱动关节臂坐标测量机面向球的最佳测量区。

2.2 测量机不同测量姿态仿真验证

针对自驱动关节臂坐标测量机测量空间内某一点在不同姿态下的测量误差，利用MATLAB进行仿真来验证单位四元数球面线性插值算法的有效性。

图5 不同测量姿态下采样点定位误差仿真

任取测量机测量空间中的采样点S1(-20 mm,546 mm,327 mm)，设定起始测量姿态和终止测量姿态的关节模组角度组合分别为[0°,5°,20°,13.2°,10°,18°]、[20°,75°,-7°,0°,4°,-20°]，利用插值法对中间姿态进行插补，进而得出该点的不同测量姿态。其中，中间插补步长设置成0.05。测量姿态总个数为21。通过MATLAB真求解，该采样点的定位误差仿真分布如图5所示。

由图5仿真曲线变化可知，当自驱动关节臂坐标测量机以21种不同姿态对空间采样点S1进行定位时，其X、Y、Z向坐标误差以及采样点定位误差存在差异。上述结果表明利用四元数球面线性插值算法可以求解出自驱动关节臂坐标测量机的不同测量姿态，同时验证了测量机以不同姿态进行测量时的工件几何特征测量误差存在差异。

3 面向标准球的最佳测量区实验验证

3.1 实验平台搭建

要研究自驱动关节臂坐标测量机的最佳测量区，需要对测量空间内不同测量区工件定位误差的分布规律进行研究，经前期研究可知自驱动关节臂坐标测量机测量空间为球体状[19]，故本文主要基于球系坐标原理，利用测量机样机对在不同测量半径r、不同测量转角φ和不同测量俯角φ空间位置处的标准球半径进行测量，研究球在测量机不同测量区域位置处的半径测量误差分布规律。其中，球坐标系原理如图6所示。

利用单一变量法通过设置6个关节模组角度组合，分别控制测量机在不同测量半径、不同测量转角和不同测量俯角状态下，其测头触测分布于球表面的4个点，研究自驱动关节臂坐标测量机测得的球半径测量误差分布规律，进而确定自驱动关节臂坐标测量机最佳测量区。自驱动关节臂坐标测量机面向球的最佳测量区实验装置如图7所示，实验设备包括测量机样机、剪式升降台、电气箱、标准球等。

图6 球坐标系原理 图7 面向标准球的自动测量实验装置

3.2 实验结果与分析

首先，为了研究自驱动关节臂坐标测量机在不同测量半径上的球半径测量误差分布，选定标准球在空间中的17组不同测量半径位置，通过不同关节之间的不同角度组合，完成自驱动关节臂坐标测量机对标准球在不同测量半径时的半径测量实验。

其次，控制测量机2～5关节角度不变，即[θ1,18°,0°,-64°,0°,51°]，仅在关节1处以10°间隔在[0°,180°]范围内转动，确定标准球的不同测量转角φ位置。

最后，控制1、3～6号关节角度不变，即[90°,θ2,0°,-75°,0°,60°]，仅在关节2处以5°间隔在[-50°,30°]范围内转动，确定标准球的不同测量俯角φ位置。

通过实验数据处理，得到自驱动关节臂坐标测量机在不同测量半径、不同测量转角和不同测量俯角处的标准球半径测量误差分布结果如图8所示。

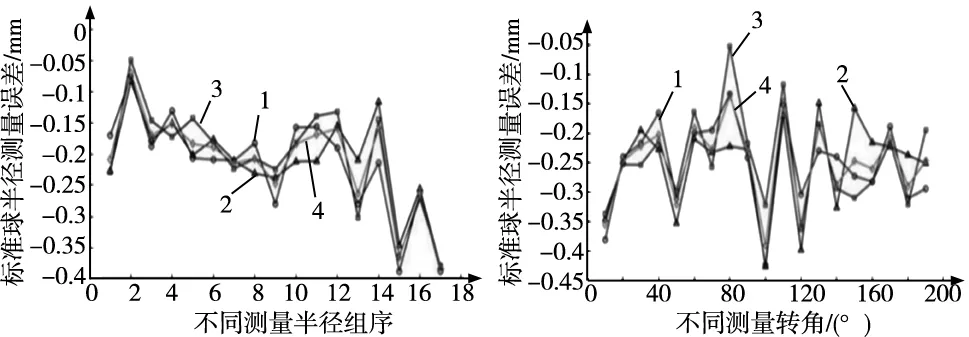
(a) 不同测量半径 (b) 不同测量转角

(c) 不同测量俯角

由图8测量实验结果得出：自驱动关节臂坐标测量机对不同空间位置处的球半径测量误差不同，且呈一定规律分布。当标准球固定于测量机的以下空间范围内，即测量半径范围为433.995 mm～659.627 9 mm，测量转角范围为130°～180°，测量俯角范围为20.102 8°～48.936 7°时，自驱动关节臂坐标测量机测得的标准球半径平均测量误差相对较小，其最大的平均测量误差值为0.332 4 mm。上述测量空间范围即为面向球的自驱动关节臂坐标测量机最佳测量区域，将待测球固定于该最佳测量区内进行半径测量时，可以有效提高测量机对球半径的测量精度。

4 结论

本文主要研究面向球的自驱动关节臂坐标测量机最佳测量区。基于自驱动关节臂坐标测量机结构原理建立了理想测量模型，确定了面向球的最佳测量区确定方法，求解了测量机测量空间同一位置工件的不同测量姿态，对空间某一采样点的不同测量姿态求解进行了仿真验证，对球坐标系下的不同半径、不同转角和不同俯角位置处的标准球进行了半径测量实验。研究结果表明，单位四元数球面线性插值算法可以实现测量机不同测量姿态的求解，在自驱动关节臂坐标测量机整个工作空间范围内，确定了面向球的自驱动关节臂坐标测量机最佳测量区。在上述区域内，自驱动关节臂坐标测量机测得的标准球半径平均测量误差相对较小，可为测量机面向复杂工件的点、线、平面等几何特征测量策略提供思路。