基于新型滑模观测器的PMSM无传感器控制*

程亚楠，刁 俊，苏子华，魏瑞丽，隋 栋

(1.中国航天科工集团第二研究院，北京 100039；2.北京航天长峰股份有限公司，北京 100039；3.北京建筑大学电气与信息工程学院，北京 102627)

0 引言

永磁同步电机(PMSM)因具有体积小、功率密度高、响应速度快等特点，在航空航天、新能源汽车、医疗器械等领域发挥着巨大的潜力[1]。在医疗器械领域的急救转运呼吸机中，通常采用永磁同步电机带动涡轮叶片压缩大气产生通气所需要的压力和流量，从而避免携带高压空气瓶，减少医护人员的救援负担。然而传统的永磁同步电机一般采用霍尔传感器或光电编码器获取转子的位置信息以控制电机的精确换向，传感器的引入不仅增加了产品的体积和成本，同时户外救援过程中的温差、噪声等不可避免的环境变化容易导致传感器损坏或者特性劣化，从而降低呼吸机系统的可靠性，对病人生命健康产生巨大的安全隐患。因此，永磁同步电机无传感器控制算法的研究对提高急救转运呼吸机系统的稳定性有着重要意义[2]。

目前永磁同步电机无传感器矢量控制算法根据基波信号的数学模型和与转速位置相关的物理量估算出转子的位置信息，常用的有模型参考自适应法(MRAS)[3-4]，扩展卡尔曼滤波法(EKF)[5-6]、滑模观测器法(SMO)[7-8]、神经网络算法[9-10]等；其中滑模观测器法具有算法简单、对模型参数变化和外部扰动不敏感等优点，在实际的电机控制领域逐渐成为主流。滑模观测器的实质是通过定子给定电流和反馈电流的误差重构反电动势，利用符号函数高频切换来不断修正反电动势，使实际电流值快速收敛于给定电流值，并从观测到的反电动势信号中提取转子的位置和转速信息[11]。符号函数的正负高频切换，导致系统在滑模态会产生固有的高频抖振，使获得的反电动势信号中含有大量的高频谐波分量。

申永鹏、张祺琛等[12-13]采用边界层厚度可变的饱和函数、分段幂函数代替符号函数，使系统在边界层内近似线性反馈控制、在边界层外为切换控制，从而减小系统在滑模态的高频抖振，但是边界层的过渡不够平滑会导致抑制抖振的效果并不明显；李垣江等[14]采用积分钳位抗积分饱和法，通过增加输入微分前馈和控制增益环节设计复合PI控制器，提高系统在负载突变时的动态响应速度；WANG、祝新阳等[15-16]引入模糊控制技术，通过电流误差和电流误差变化率的关系设计模糊规则对观测器的滑模增益进行实时调整，从而提高系统的动态响应速度并削弱固有的系统抖振，但是此方法仅适用于调速范围比较小的电机控制系统，呼吸机中永磁同步电机的调速范围比较大，通常在每分钟几千至几万转用以满足通气过程中所需压力和流量控制的实时性要求，因此该方法的实际效果并不明显。

本文提出一种新型滑模观测器算法，将其应用于急救转运呼吸机永磁同步电机控制，能够有效提高通气过程中压力和流量的控制精度，改善其通气性能，对急救转运呼吸机产业化发展具有重要意义。

1 传统滑模观测器原理

根据永磁同步电机(PMSM)中永磁体的安装位置不同，大致分为内嵌式和表贴式两种。本文中PMSM采用表贴式永磁同步电机，在两相静止坐标系下的数学模型[17]为：

(1)

式中，iα、iβ、uα、uβ分别为两相静止坐标系下的定子电流和电压；Rs、Ls分别为定子电阻和电感；ke为反电动势系数；ωe为转子角速度；θe为转子角度；eα、eβ分别为两相静止坐标系下的反电动势，从上式可以看出反电动势信号中包含转子的位置信息。

滑模观测器状态方程的数学表达式为：

(2)

(3)

式中，ωr为低通滤波器的截止频率。将滤波后的反电动势进行反正切函数计算得到转子的位置，进而微分得到转子的角速度。

(4)

2 新型滑模观测器算法设计

2.1 sigmoid(x)函数

针对符号函数在零点不连续引起的系统抖振问题，本文采用零点光滑连续的sigmoid(x)函数代替符号函数sign(x)，函数图像如图1所示。

图1 sigmoid函数示意图

sigmoid(x)函数在整个实数域内光滑连续，并在零点周围近似线性关系，能够有效抑制切换状态因零点不连续产生的系统抖振。其中控制系数a用于调节零点附近的曲线斜率，a值越大，曲线越陡，越接近符号函数；变量Δ为边界层厚度，在边界层内采用sigmoid函数，在边界层外采用符号函数，边界层厚度越大，抑制系统抖振的效果越好，控制精度越高，但是会降低系统的响应速度。因此选择合适的a和Δ对满足系统的控制精度和响应速度至关重要。考虑电流误差的变化范围，本文选取a=3，Δ=2，此时滑模观测器的切换函数变为：

(5)

2.2 自适应滑模增益设计

传统的滑模增益是人为根据经验设定的常数。滑模增益越大，趋近运动的速度越高，到达滑模面的时间越短，系统的响应速度越快，但是在低转速时系统的抖振也会更剧烈。对于调速范围大的呼吸机用PMSM控制系统，固定常数的滑模增益难以同时满足抑制系统抖阵和提高响应速度的需求。根据式(1)中反电动势方程可以看出，反电动势的大小和转子的转速成正比，本文设计一种滑模增益跟随转速变化的自适应律：

(6)

分别针对低速和高速，分段设置不同的自适应律。式(6)中，Ksw为滑模增益值；ω0、ω1为额定转速参考值；K0、K1为增益基准值；c0、c1为增益偏移值；ωref为转速实际值。当系统运行在低转速时，通过减小滑模增益抑制系统的高频抖阵；当系统运行在高转速时，通过增大滑模增益提高系统的响应速度。

2.3 自适应滑模观测器设计

传统滑模观测器得到的反电动势信号中存在大量的高频谐波分量，经过低通滤波器处理后的反电动势信号存在明显的相位延迟。为了得到精确的转子位置，需要增加相位补偿环节[18]，相位补偿通常与低通滤波器的截止频率和电机的转速有关，一方面滤波器的截止频率恒定，随着转速的提升，截止频率引起的相位延迟会不断增大，从而破坏系统的稳定性；另一方面，转速的观测误差被直接引入补偿环节，导致转子位置的观测精度下降。除此之外，相位补偿的反正切运算还会占用大量的CPU和内存资源。

为了解决上述相位补偿产生的问题，本文设计一种新型的自适应滑模观测器。自适应滑模观测器状态方程的数学表达式为：

(7)

根据电流的观测值和实际值误差，得到电流的误差方程：

(8)

(9)

设计反电动势自适应律：

(10)

由于电机的电气时间常数远小于机械时间常数，在一个控制周期中，转子转速变化几乎为0，进而得到反电动势误差方程：

(11)

(12)

(13)

式(13)满足Lyapunov稳定性理论，证明自适应滑模观测器算法是稳定的。此时传统二阶滑模观测器变为四阶自适应滑模观测器，在MCU中编写程序需要对四阶观测器方程进一步离散化处理：

(14)

式中，Ts为电流采样周期；k为滑模增益；m为反电动势误差增益。

在得到反电动势观测值后，传统滑模观测器采用反正切函数计算转子位置。反电动势信号中的高频抖振和观测误差被直接引入反正切函数的除法运算中，导致结果的误差被放大，进而降低转子位置的观测精度。本文采用锁相环[19](PLL)来提取转子的位置信息，如图2所示。

图2 锁相环结构原理图

根据图2可得如下表达式：

(15)

3 仿真验证和结果分析

为了验证本文所设计的新型滑模观测器算法在PMSM调速系统中的性能，在MATLAB/Simulink平台上搭建永磁同步电机无传感器矢量控制系统，系统结构框图如图3所示。表贴式PMSM的电机参数为：定子电阻Rs=0.02 Ω，定子电感Ls=0.015 mH，反电动势系数Ke=0.1Vrms/krpm，极对数ρ=1，转动惯量J=0.135 μN·m·s2，粘滞系数F=1.824 μN·m·s。仿真选用定步长ode3算法，采样时间设置为2×10-6s。

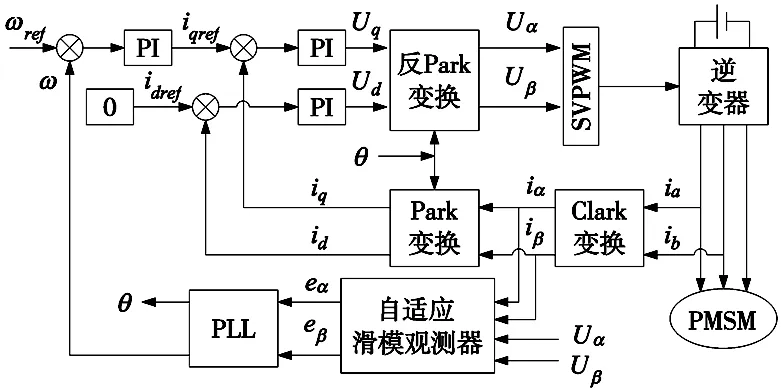
图3 永磁同步电机无传感器矢量控制系统

为了更直观分析系统的动态性能和新型滑模观测器的改进效果，将传统滑模观测器和新型滑模观测器进行对比实验。图4～图7表示传统和新型滑模观测器在永磁同步电机1000 r/min运行时的转子转速、转子位置、反电动势和负载转矩观测曲线图。

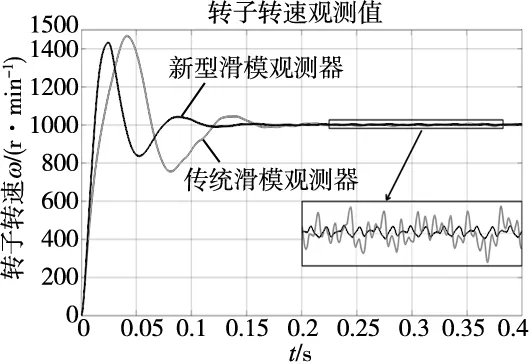
图4 传统及新型滑模观测器转子转速对比

从图4可以看出，新型滑模观测器在启动过程中转速收敛速度更快，有更小的超调量；在电机稳定运行时高频分量和系统抖阵明显减小，转速的观测误差率从1%降低到3‰，观测精度显著提高，能够有效降低呼吸机通气过程中压力和流量的波动，从而提高呼吸机通气系统的控制精度。

从图5a和图5b转子位置实际值和观测值曲线可以看出，新型滑模观测器在电机稳定运行时对转子位置的跟踪效果更好，相位延迟分别为4.112 ms和2.816 ms，新型滑模观测器产生的相位延迟更小，相位延迟减少31.5%；从图5c转子位置观测误差曲线可以看出，最大转子位置观测误差分别为29.1°和20.3°，转子位置的观测误差率从8.1%降低到5.6%，新型滑模观测器在系统稳定运行时对转子位置的观测精度更高。

(a) 传统滑模观测器转子位置实际值和观测值 (b) 新型滑模观测器转子位置实际值和观测值

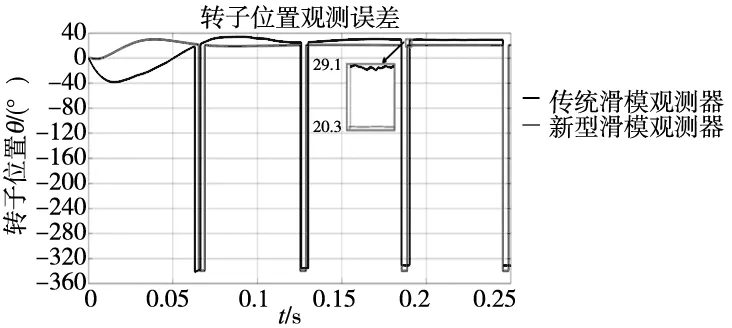
(c) 传统及新型滑模观测器转子位置观测误差值

从图6反电动势观测曲线可以看出，传统滑模观测器在经过低通滤波后得到的反电动势信号中仍含有大量的高频谐波；新型滑模观测器通过设计自适应律算法对观测的反电动势进行实时修正，弥补了传统滑模观测器中高频切换信号产生的固有抖阵缺陷，使得到的反电动势信号中几乎无高频分量，观测曲线近似正弦曲线，反电动势的观测精度大幅度提高。

(a) 传统滑模观测器反电动势观测值 (b) 新型滑模观测器反电动势观测值

图7是在0.4 s突加4 N负载时转子转速和负载转矩的观测值变化曲线。

(a) 转子转速观测值 (b) 电磁转矩观测值

从图7a可以看出，新型滑模观测器在负载突变时对转速有良好的跟踪效果。从图7b可以看出，传统和新型滑模观测器的最大转矩误差分别是0.4 N·m和0.15 N·m，最大转矩误差率从3.8%降低到1.43%，新型滑模观测器的转矩曲线更加平滑，观测精度更高，抑制系统抖阵效果更好。

为了更好地验证新型滑模观测器算法在抑制系统抖振方面的效果，将文献中提到的饱和函数、分段幂函数和本文设计的sigmoid函数进行对比分析，如图8所示。

(a) 转子转速对比 (b) 转子位置对比

从图8a可以看出，在抖阵频率相同的情况下，sigmoid函数的转速误差值最小，观测精度最高。从图8b可以看出，sigmoid函数的相位延迟最小，对转子位置的跟踪效果最好。

为了更好地分析自适应滑模增益在提高系统观测精度方面的效果，在转速一定的条件下，将常数滑模增益和自适应滑模增益进行对比分析，如图9所示。

图9 新型滑模观测器中常数滑模增益和自适应滑模增益转速观测值对比

实验中调节永磁同步电机转速从5000 r/min到10 000 r/min到15 000 r/min再到20 000 r/min。从图中可以看出，低速下的常数滑模增益在电机高速运行时会导致转速的观测误差增大，观测精度下降。引入随转速变化的自适应滑模增益能够有效提高转子转速的观测精度，从而进一步提高呼吸机通气系统的稳定性。

4 实物验证和结果分析

为了验证本文提出的新型滑模观测器算法的可行性和上述仿真实验的有效性，根据图3搭建永磁同步电机无传感器矢量控制实验平台，实验平台由直流电源、上位机、永磁同步电机、涡轮风机模块(负载)、电机控制驱动器、示波器、高精度转速测量仪等部分组成，如图10所示。其中电机控制器采用意法半导体的STM32G431CB型号芯片。

图10 永磁同步电机无传感器矢量控制实验平台

本实验采用双闭环矢量控制方式，转速环和电流环的控制频率分别是1 kHz和20 kHz，转速环主要用于执行状态机和计算转速平均值；电流环用于执行观测器状态方程、计算转子角度、ADC三相电流采样、数学计算(clark、park、反park变换)和SVPWM计算三相电压输出占空比等。实验结果如图11～图14所示。

图11为新型滑模观测器转子转速设定值和观测值曲线，转速的采样周期为10 ms，调节转子转速设定值从5000 r/min到10 000 r/min到15 000 r/min再到20 000 r/min。从图中可以看出，自适应滑模增益的设计抑制了转速突变引起的超调，超调量在8%左右；随着转速上升，系统高频抖阵越来越小，观测精度越来越高；新型滑模观测器在转速突变时对转子转速有良好的跟踪效果，能够满足呼吸机通气系统响应速度快的要求。

图11 新型滑模观测器转子转速设定值和观测值对比

图12～图14是新型滑模观测器在转子转速为10 000 r/min稳定运行时三相电流、反电动势和转子位置观测曲线，观测值的采样周期为50 μs。

图12 新型滑模观测器三相电流变化

图13 新型滑模观测器反电动势观测值

图14 新型滑模观测器转子位置观测值

从图12可以看出，三相电流波形无明显纹波，相位互相延迟120°。从图13可以看出，反电动势波形无高频谐波分量，观测曲线近似正弦曲线。从图14可以看出，转子位置观测曲线近似直线，观测器能够准确跟踪转子的实际位置，观测精度高。

5 结论

本文通过对传统滑模观测器存在的系统抖阵大、观测精度低、动态响应速度慢等问题进行分析，提出了一种新型自适应滑模观测器算法。采用零点连续的sigmoid函数代替符号函数，能够有效抑制系统在滑模面高频切换产生的抖阵，使电机运行时的转速和转矩更加平稳，从而提高了呼吸机通气过程中压力和流量的控制精度；设计自适应滑模增益和反电动势自适应律，能够有效降低大范围调速引起的观测误差，提高系统抗干扰能力的同时进一步加快电机的转速收敛，从而缩小吸气过程中输送气体的时间，提高了通气系统的动态响应速度。实验结果证明了本文所提方法的有效性，新型滑模观测器算法对急救转运呼吸机产业化发展具有重要意义。