简谐激励下阻尼复合结构多尺度拓扑优化设计

倪维宇，张横，姚胜卫

缓冲与隔振

简谐激励下阻尼复合结构多尺度拓扑优化设计

倪维宇a，张横b，姚胜卫a

（上海理工大学 a.公共实验中心 b.机械工程学院，上海 200093）

为得到抗振性能良好的板壳结构，保证设备的正常工作，文中提出一种板壳阻尼复合结构多尺度优化设计方法。以动柔度为目标，建立频域激励下和固定频率点激励下板壳阻尼复合结构中阻尼材料宏观分布和微结构协同设计的多尺度问题的数学模型，推导目标函数和约束条件对设计变量的灵敏度，并基于移动渐近线法求解优化数学模型。所提多尺度设计方法可以有效获得板壳结构最优阻尼材料宏观布局和最优阻尼复合材料微结构构型，提高了结构的动力学性能，同时结果也表明涂敷阻尼复合材料结构的振动响应相较于仅涂敷单一阻尼材料的振动响应大幅减小。研究表明，不同激励频率下阻尼材料的宏观分布形态不同，阻尼材料主要分布于结构模态振型位移的最大处和支撑端，通过加强结构的刚度，抑制了结构变形，减小了振动响应。微结构构型基本类似，其基本形态都是低刚度、高阻尼材料呈条状分布，条状分布的阻尼复合材料微结构在受弯方向上的刚度较大，可以有效抵制结构的弯曲变形。

阻尼复合结构；多尺度；拓扑优化；阻尼层；简谐激励

随着尖端科技的不断发展，高精度的产品设备在包装以及运输过程中对包装材料的隔振降噪的要求越发严格。在大面积的板壳包装材料中，外部激励产生的振动往往需要一定的消退时间，板壳振动问题在包装工程中显得尤为突出，因此，低质量、高刚度特性板壳材料的振动特性研究近年来成为新的研究热点。在包装工程的振动控制领域，通常希望在一定的设计条件下有效降低振动的幅值，以提高设备结构的工作精度和可靠性。在设备结构上增加阻尼材料形成复合结构，是控制结构振动的有效办法，通过阻尼材料的耗能实现减小振动幅值和快速衰减振动的目的，如运载装备中承受动态载荷的板壳结构，可通过对阻尼层的优化设计减小板壳结构振动响应，减小噪声，提高舒适性，因此，针对结构动态载荷的响应最小化问题开展研究具有重要价值。

在阻尼复合结构宏观分布设计方面，Kang等[1]以简谐激励响应最小为目标对壳结构的阻尼材料分布进行了设计。Kim等[2]通过将结构模态的阻尼比最大作为设计目标，以壳结构阻尼材料的分布为研究对象进行了设计。Yamamoto等[3]基于改进的模态应变能法，将系统的模态阻尼比最大为优化目标，研究了板壳结构的阻尼层优化问题。Takezawa等[4]以减小共振响应幅值为目标，研究了阻尼材料的最优分布问题，实现最小的附加质量条件下得到最优阻尼材料分布形式。房占鹏等[5]优化了频带激励下阻尼材料的分布。蒋亚礼等[6]、贺红林等[7]同样研究了阻尼材料的分布问题。尽管阻尼材料的分布设计可以有效提高结构阻尼，但是由于高阻尼材料（如橡胶）模量小、密度大的特点，不可避免地会减小原结构的动刚度，由此可能引发新的振动问题，因此在不降低结构刚度的前提下，对结构阻尼的优化设计就显得尤为重要。从材料设计的角度出发，通过对复合材料微结构的构型设计，使得设计的复合材料兼具高刚度高阻尼特性，有效提高结构的刚度和阻尼。

针对材料微结构设计问题，Yi等[8-10]研究表明复合材料的刚度和阻尼与其微结构构型有关，以提高材料阻尼为目标，采用逆均匀化方法，实现了复合材料的微结构设计。Chen等[11]研究了材料剪切模量与阻尼之间的关系，以剪切模量最大为目标进行设计。Huang等[12]对优化目标的选择在阻尼复合材料中的影响进行了研究，分析了刚度和阻尼作为设计目标对微结构构型的影响。上述的研究都是针对复合材料微结构进行研究的，设计目标多为复合材料的材料属性，如阻尼、刚度等，而非兼顾到关于复合材料结构设计问题。再例如，以结构的宏观性能为目标进行研究时，Liu等[13]在对阻尼复合结构的微结构进行设计时，是在以结构频率为约束的前提下完成的。Chen等[14]同样是以结构模态阻尼比为目标，经过优化实现了复合结构的振动响应值都有所减小。Andreassen等[15]研究了一种关于阻尼结构的多尺度设计方法，通过最大化阻尼复合材料微结构的阻尼性能，在获得阻尼复合材料微结构构型的优化结果后，再采用优化已经得到的微结构构型在宏观上进行优化，进而得到其宏观上的最优分布，但该研究方法实际上仍是2个单尺度设计方法，并非多尺度设计方法。Zhang等[16]以结构模态阻尼比最大为目标，对自由阻尼层结构的多尺度设计问题进行了研究，并未对动力学响应问题进行研究。

目前，关于阻尼复合结构的优化设计研究多数停留在仅宏观尺度或仅微观尺度，而多尺度设计的研究较少，但其可以在保证不降低结构性能的前提下最大限度的节省材料。基于以上分析，文中对阻尼复合结构在给定简谐激励下的响应问题进行优化设计，研究在动态载荷作用下阻尼复合结构的两尺度设计问题，如何对阻尼材料的分布以及阻尼材料微结构同时进行设计，进行优化设计问题的灵敏度分析，以结构柔度为目标，分别对频带激励下和固定频率点激励下的阻尼复合结构进行两尺度拓扑优化设计。

1 阻尼复合结构的动柔度

=T(1)

式（1）为动柔度定义，为结构的位移列阵，为载荷向量。由于阻尼材料的作用，结构的位移列阵为复数，因此动柔度也是复数，其表达式为：

=R+iI(2)

式中：R、I分别为动柔度的实部和虚部。

根据式（2），动柔度又可表示为：

根据式（1）、式（2）可得，

=T=T(R+ iI‒2)(4)

将结构的位移列阵表示为复数形式，式（4）可改写为式（5）所示形式。

经整理得：

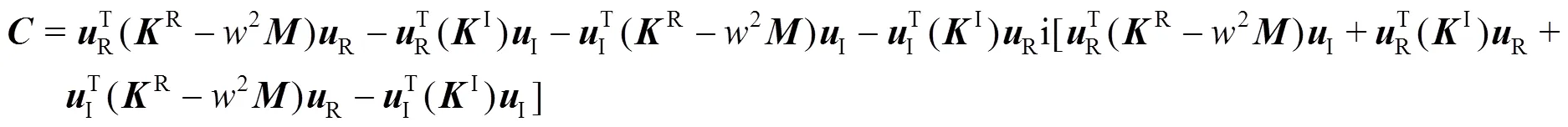
根据式（6），可得R，I分别为：

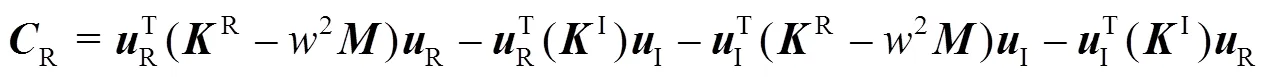
2 优化数学模型及灵敏度分析

以结构的动柔度最小为目标对阻尼复合结构进行两尺度优化设计，其数学模型为：

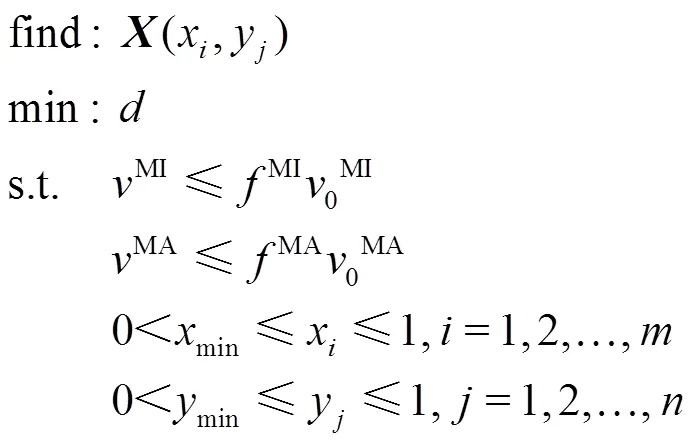
式中：为设计变量，其中x为微结构设计变量、y为基板上宏观分布的设计变量；为结构的动柔度；0MI、0MA分别为宏微观原始结构体积；MI、MA分别为宏微观优化后结构体积；MI、MA分别是宏微观体积分数。

杜建镔等[17]对动柔度设计中激励频率对设计结果的影响问题进行了详细研究，指出在外部激励略小于结构的固有频率时比在外部激励略大于结构固有频率时可得到更理想的设计结果，但若实际激励频率大于结构固有频率时，可通过频率渐变的方法对结构进行动柔度最优化设计。为了减小结构在固有频率附近的响应，文中将激励频率均设置为略小于结构的固有频率，以得到理想的设计结果。

通过对式（3）求导，可得到目标函数动柔度对设计变量的灵敏度：

式（10）中R，I对设计变量的灵敏度分别为：

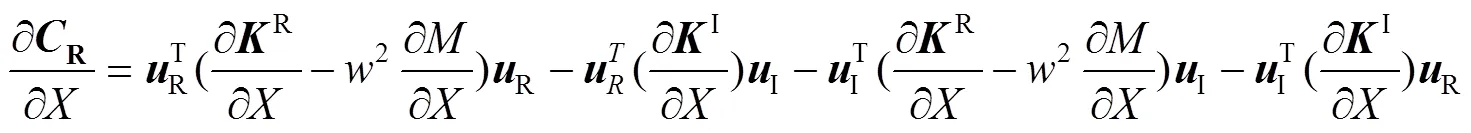
由于基板为非设计域，因此R对微观和宏观设计变量（x,y）的灵敏度可根据式（13）和式（14）计算得到。

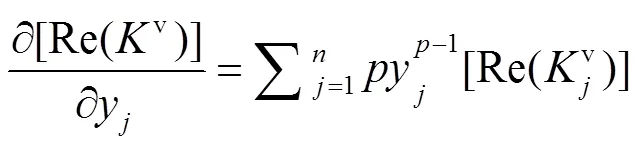
I对微观和宏观设计变量(xy)的灵敏度可根据式（15）和（16）计算得到。

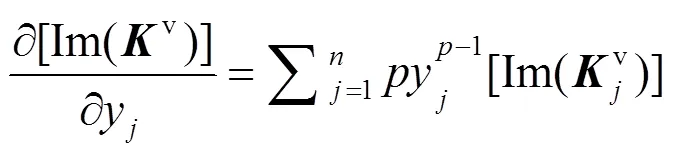
质量矩阵分别对微观设计变量x和宏观设计变量y的灵敏度为：

将式（13）、（15）、（17）和式（14）、（16）、（18）分别代入式（11）和（12）即可得到动柔度目标函数分别对微观设计变量x和宏观设计变量y的灵敏度。

3 设计流程

将基板为非设计域，阻尼层为设计域，建立自由阻尼层两尺度的优化模型。通过对微结构中单胞进行模型，将其所有的单元设定为设计变量，采用均匀化方法进行分析，可得单胞模型的等效复弹性矩阵。然后对结构宏观性能进行有限元分析，借助已得到的单胞等效复弹性矩阵对目标函数和约束函数进行计算，从而得到复合结构的整体性能。最后进行2个尺度上的灵敏度分析，基于移动渐进算法更新设计变量x和y，当目标函数优化过程中相连2次的差值小于允许的容差，或触发迭代次数上限时，则退出寻优，否则返回微结构有限元分析，继续优化，迭代至收敛条件。具体优化流程见图1。对阻尼复合材料两尺度优化数学模型式（9）的求解，可通过移动渐进算法寻优得到。

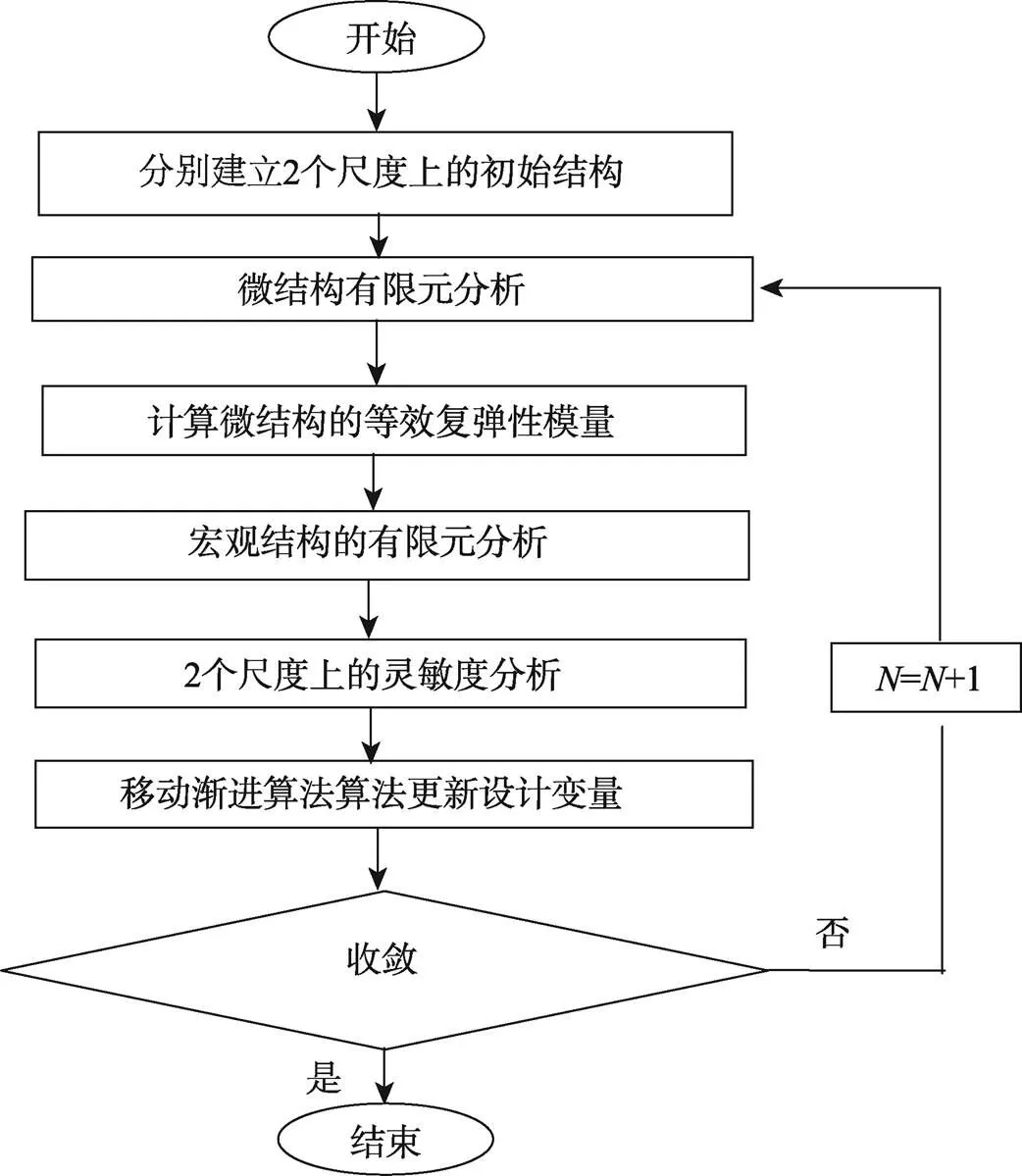
图1 阻尼复合结构的多尺度设计流程

4 算例

以图2a所示悬臂板结构为例，其长度=150 mm、宽度=100 mm，金属基板和阻尼层的厚度均为2 mm。激励点为图2a中的圆点，其位于矩形板最右端中间位置。图2b为简谐激励载荷，激励幅值为100 N。对于频域激励，文中算例都是均匀选取11个频率点。算例中金属板的材料为铝合金，阻尼层中的两相材料为橡胶和树脂，分别代表2种典型的材料性能——低刚度高阻尼材料和高刚度低阻尼材料，材料性能见表1。

4.1 频域激励下的两尺度设计

对图2所示的悬臂板结构进行设计，宏微观体积分数分别为MA=0.5和MI=0.8。由于不同初始构型对设计结果有一定影响，故在不同初始构型下对结构进行两尺度设计，初始构型见图3。结构在不同初始微结构下初始结构的前三阶固有频率分别约为75、250和450 Hz，因此在频段激励优化设计中，首先将激励频段设置为60～70 Hz，建立4种结构：model 1的初始微结构1，=7.304、MA=0.38、MI=0.49；model 2的初始微结构2，=6.932、MA=0.39、MI=0.58；model 3的初始微结构3，=6.538、MA=0.41、MI=0.72；model 4的初始微结构4，=6.648、MA=0.41、MI=0.66。4种设计结果见图4。从图4结果可知，model 1、model 2、model 3、model 4这4种结构的材料宏观分布基本相同，阻尼复合材料均分布与板的左侧部分，微结构构型基本类似，低刚度高阻尼材料的体积分数略有不同，其基本形态都是低刚度高阻尼材料分布，即呈条状分布，由于加载点的位置在结构上下对称的中心线上，因此结构主要受到弯矩作用，发生弯曲变形，条状分布的阻尼复合材料微结构在结构受弯方向上的模量较大，可以有效抵制结构的弯曲变形，因此最终的阻尼复合材料微结构形态都类似。

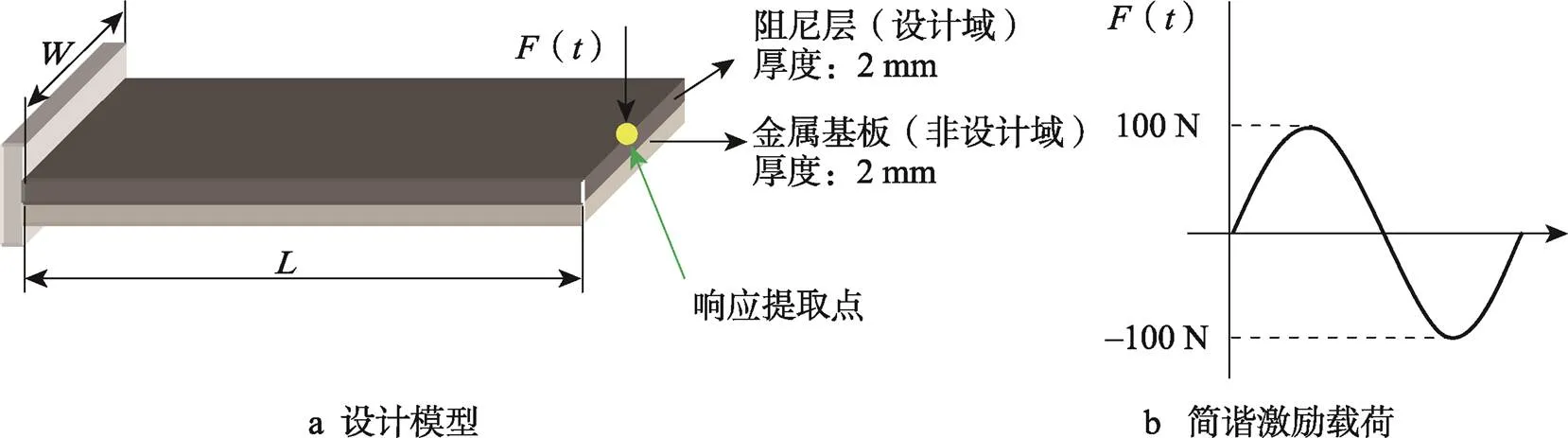
图2 悬臂板结构激励位置示意

表1 基板和阻尼材料的性能

Tab.1 Properties of substrates and damping materials

图3 不同的初始微结构构型

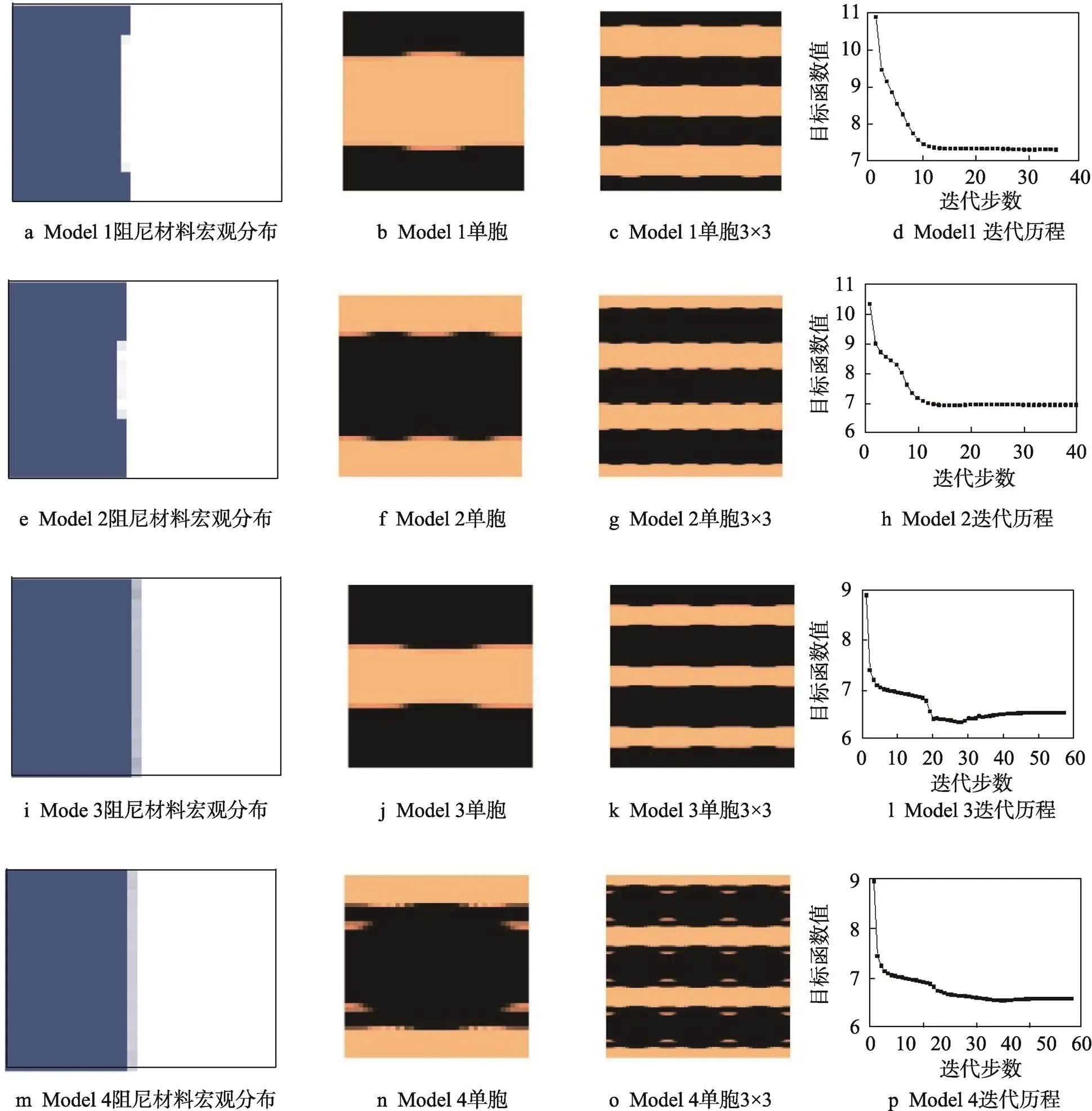
图4 悬臂板激励频率在60～70 Hz时设计结果

由于激励频段发生在基频附近，结构的振动响应主要是第1阶模态起主要作用，因此结构宏观的材料分布于结构支撑端，从而来加强结构，以提高结构基频，减小振动响应。从图4的迭代历程中可以看出，不同初始构型下的设计结果都最终收敛。从目标函数值可以看出，初始构型4得到的设计结果的目标值最小，此时微结构中高阻尼相的体积分数为0.66。初始构型3得到的设计结果的目标函数值比初始构型4得到设计结果的目标函数值略大，同时其高阻尼相材料的体积分数是最大的。

4.2 固定频率激励下的两尺度设计

对固定频率激励下结构的响应最小化问题进行设计，激励频率设置为65 Hz，略小于初始结构的基频，设计的4种结构：model 5的初始微结构1，=0.638、MA=0.40、MI=0.49；model 6的初始微结构2，=0.608、MA=0.41、MI=0.58；model 7的初始微结构3，=0.565、MA=0.41、MI=0.68；model 8的初始微结构4，=0.595、MA=0.41、MI=0.63。4种设计结果见图5。从图5中可以看出，4种不同构型下阻尼材料的宏观分布基本相同，均分布于板的左侧部分，与60～70 Hz频段激励下的设计结果相同，均是因为激励频率发生在结构基频附近，结构第1阶模态起主导作用，故对第1阶模态进行抑制以减小目标函数值。4种不同初始构型下设计结果的微结构构型基本类似，且在相同的初始构型下与60～70 Hz频段激励下的设计结果相同，不同初始构型下设计结果微结构中低刚度高阻尼材料体积分数略有不同。从目标函数值可以看出，初始构型3得到的设计结果的目标函数值最小，此时微结构中高阻尼相的体积分数为0.68。

通过对不同的初始构型下，以动柔度为目标的阻尼复合结构两尺度设计问题进行研究，证明了该设计方法可用于不同初始构型下的设计，同时设计结果也表明初始构型3下得到的结果最优。当悬臂板激励频率为235 Hz，初始构型为3时的设计结果，如图6所示（激励频率235 Hz，初始微结构3，=0.103、MA=0.49、MI=0.62），可知阻尼材料的宏观分布与激励频率为65 Hz时不同，主要是因为65 Hz接近于结构的第1阶固有频率，故第1阶模态的响应起主要作用，而235 Hz接近于结构的第2阶固有频率，所以第2阶模态的响应起主要作用。优化后微结构的形态基本相同，低刚度高阻尼材料的体积分数为0.62。悬臂板激励频率为420 Hz时，初始构型为3时的设计结果如图7所示（激励频率为420 Hz，初始微结构3，=0.300、MA=0.40、MI=0.62），可知阻尼材料的宏观分布与激励频率为65 Hz和235 Hz时的不同，主要是因为420 Hz接近于结构的第3阶固有频率，第3阶模态的响应起主要作用，微结构的形态与上述算例基本相同。

图5 悬臂板激励频率为65 Hz时设计结果

5 实验验证及分析

为了验证设计结果的正确性，故对设计结果进行试验测试，根据实验测试结果判断设计方法以及设计结果的优劣性，实验测试方案布置见图8，对结构左侧夹紧以模拟悬臂板结构。根据4.1节和4.2节算例结果可知，设计结果中微结构构型形态基本相同，都是低刚度高阻尼材料呈条状分布，不同之处仅是体积分数有略微区别，对比不同微结构初始构型设计结果可知，最优的微结构中低刚度高阻尼材料的体积分数约为0.7，故实验中仅取体积分数为0.7的结构进行制作，并分别制作了微结构中仅有低刚度高阻尼材料和仅有高刚度低阻尼材料的试件，如图9所示，3个样件中铝合金板厚度均为0.8 mm，都是整板左侧涂敷50%，图9a为左侧涂敷环氧树脂，图9b为左侧涂敷橡胶，图9c左侧是涂敷微结构（橡胶的体积分数为0.7）。

图6 悬臂板激励频率为235 Hz时设计结果

图7 悬臂板激励频率为420 Hz时设计结果

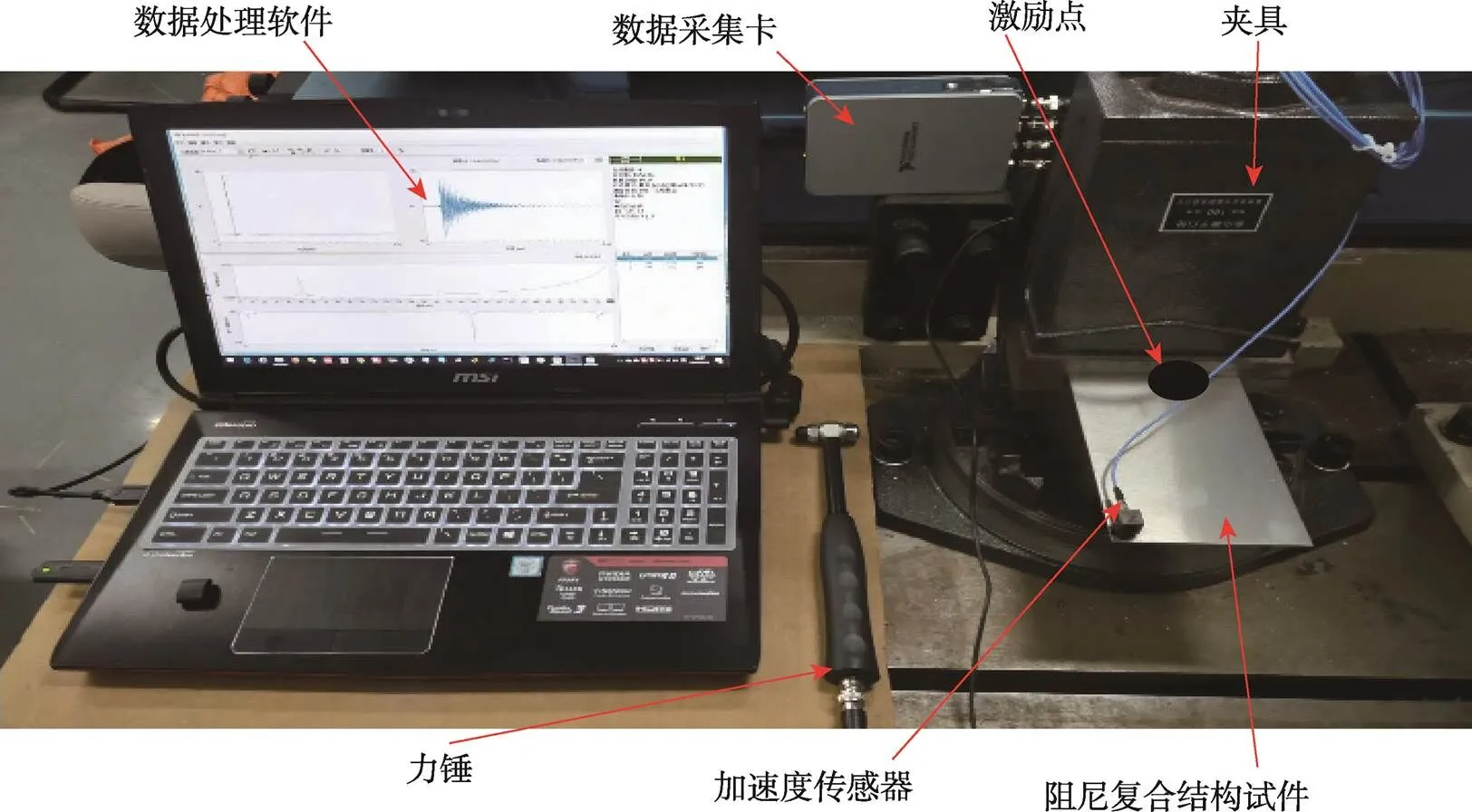
图8 两尺度阻尼复合结构实验方案布置

图9 不同微结构形态的阻尼复合结构的实物

表2 两尺度设计悬臂板仿真与实验对比

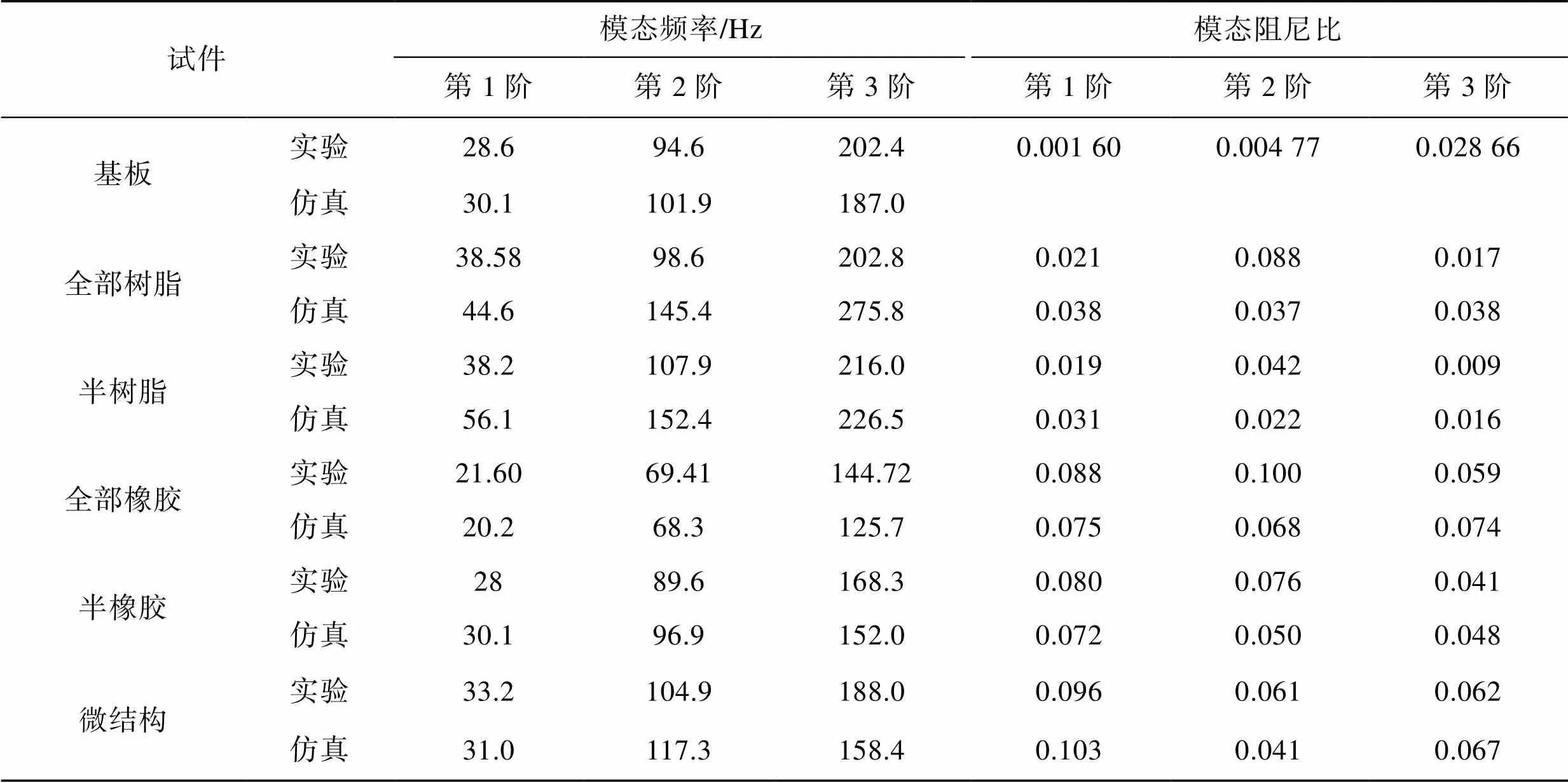
Tab.2 Comparison between simulation and experiment of cantilever plate with two scale design

图10 实验测试频率响应

经过实验测试，得到结构频率响应见图10，表2为实验测试结果，尽管两尺度设计的悬臂板实验测试结果与仿真存在一定的误差，但由于实验都是在相同实验条件下进行，因此实验仍可反映设计结果的性能。

在结构左侧涂敷橡胶相较于全涂敷橡胶，实验测试和仿真结果都表明结构的刚度增加，但结构的阻尼减小，以实验结果为例，全部涂敷橡胶结构的第1阶频率和阻尼分别为21.6 Hz和0.088，左侧涂敷橡胶的第1阶频率和阻尼分别为28.0 Hz和0.080，结构的频率响应幅值变大；结构左侧涂敷环氧树脂相较于全涂敷环氧树脂，仿真结果中结构的前两阶频率增加。第3阶频率减小，实验结果中结构的频率变化不大，实验和仿真结果都表明结构的阻尼减小，同样结构的频率响应幅值变大，左侧涂敷环氧树脂的板结构其各阶模态频率是最大的；而涂敷阻尼复合材料的结构，见图9c。虽然其各阶模态频率略小于左侧涂敷环氧树脂结构，但其频率响应在所有结构中响应是最小的，同时仿真和实验结果都表明，涂敷阻尼复合材料的结构的模态阻尼在所有结构中是最大的。与基板结构相比，涂敷阻尼复合材料的结构其前两阶模态频率都大于基板，频率响应减小了约8倍，因此，合理的微结构形式可以使用最少的材料达到最优的结构性能，有效地减小结构的振动响应。

6 结语

基于变密度法对阻尼复合结构的两尺度优化问题进行研究，通过两尺度拓扑优化方法实现阻尼复合材料的微结构设计及其在宏观上的最优分布设计。以结构动柔度为目标对阻尼复合结构进行设计研究，分别对频域激励下和固定频率点激励下板壳阻尼复合结构进行两尺度设计。不同激励频率下阻尼材料的宏观分布形态不同，阻尼材料主要分布在结构模态振型位移最大处和支撑附件处，通过增加结构刚度来抑制结构变形，减小振动响应。由于加载位置位于结构中线上，使得不同激励频率下微结构构型基本类似，其基本形态都是低刚度高阻尼材料呈条状分布。条状分布的阻尼复合材料微结构在受弯方向上的刚度较大，可以有效抵制结构的弯曲变形。

[1] KANG Zhan, ZHANG Xiao-peng, JIANG Shi-gang, et al. On Topology Optimization of Damping Layer in Shell Structures under Harmonic Excitations[J]. Structural and Multidisciplinary Optimization, 2012, 46(1): 51-67.

[2] KIM S Y, MECHEFSKE C K, KIM I Y. Optimal Damping Layout in a Shell Structure Using Topology Optimization[J]. Journal of Sound and Vibration, 2013, 332(12): 2873-2883.

[3] YAMAMOTO T, YAMADA T, IZUI K, et al. Topology Optimization of Free-Layer Damping Material on a Thin Panel for Maximizing Modal Loss Factors Expressed by only Real Eigenvalues[J]. Journal of Sound and Vibration, 2015, 358: 84-96.

[4] TAKEZAWA A, DAIFUKU M, NAKANO Y, et al. Topology Optimization of Damping Material for Reducing Resonance Response Based on Complex Dynamic Compliance[J]. Journal of Sound and Vibration, 2016, 365: 230-243.

[5] 房占鹏, 郑玲, 唐重才. 指定频带简谐激励下约束阻尼结构拓扑优化[J]. 振动与冲击, 2015, 34(14): 135-141.

FANG Zhan-peng, ZHENG Ling, TANG Zhong-cai. Topology Optimization for Constrained Layer Damping Structures under Specified-Band Harmonic Excitations[J]. Journal of Vibration and Shock, 2015, 34(14): 135-141.

[6] 蒋亚礼, 吕林华, 杨德庆. 提高船用阻尼材料应用效果的优化设计方法[J]. 中国舰船研究, 2012, 7(4): 48-53.

JIANG Ya-li, LYU Lin-hua, YANG De-qing. Design Methods for Damping Materials Applied to Ships[J]. Chinese Journal of Ship Research, 2012, 7(4): 48-53.

[7] 贺红林, 袁维东, 夏自强, 等. 约束阻尼结构的改进准则法拓扑减振动力学优化[J]. 振动与冲击, 2017, 36(9): 20-27.

HE Hong-lin, YUAN Wei-dong, XIA Zi-qiang, et al. Topology Optimization of Plates with Constrained Damping Based on Improved Optimal Criteria[J]. Journal of Vibration and Shock, 2017, 36(9): 20-27.

[8] YI Y M, PARK S H, YOUN S K. Asymptotic Homogenization of Viscoelastic Composites with Periodic Microstructures[J]. International Journal of Solids and Structures, 1998, 35(17): 2039-2055.

[9] YI Y M, PARK S H, YOUN S K. Design of Microstructures of Viscoelastic Composites for Optimal Damping Characteristics[J]. International Journal of Solids and Structures, 2000, 37(35): 4791-4810.

[10] ANDREASSEN E, JENSEN J S. Topology Optimization of Periodic Microstructures for Enhanced Dynamic Properties of Viscoelastic Composite Materials[J]. Structural and Multidisciplinary Optimization, 2014, 49(5): 695-705.

[11] CHEN Wen-jiong, LIU Shu-tian. Topology Optimization of Microstructures of Viscoelastic Damping Materials for a Prescribed Shear Modulus[J]. Structural and Multidisciplinary Optimization, 2014, 50(2): 287-296.

[12] HUANG Xiao-dong, ZHOU Shi-wei, SUN Guang-yong, et al. Topology Optimization for Microstructures of Viscoelastic Composite Materials[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 283: 503-516.

[13] LIU Qi-ming, RUAN Dong, HUANG Xiao-dong. Topology Optimization of Viscoelastic Materials on Damping and Frequency of Macrostructures[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 337: 305-323.

[14] CHEN Wen-jiong, LIU Shu-tian. Microstructural Topology Optimization of Viscoelastic Materials for Maximum Modal Loss Factor of Macrostructures[J]. Structural and Multidisciplinary Optimization, 2016, 53(1): 1-14.

[15] ANDREASSEN E, JENSEN J S. A Practical Multiscale Approach for Optimization of Structural Damping[J]. Structural and Multidisciplinary Optimization, 2016, 53(2): 215-224.

[16] ZHANG Heng, DING Xiao-hong, LI Hao, et al. Multi-Scale Structural Topology Optimization of Free-Layer Damping Structures with Damping Composite Materials[J]. Composite Structures, 2019, 212: 609-624.

[17] 杜建镔. 结构优化及其在振动和声学设计中的应用[M]. 北京: 清华大学出版社, 2015: 89-92.

DU Jian-bin. Structural Optimization and Its Application in Vibration and Acoustic Design[M]. Beijing: Tsinghua University Press, 2015: 89-92.

Multi-scale Topology Optimization Design for Damping Composite Structures under Harmonic Load

NI Wei-yua,ZHANG Hengb,YAO Sheng-weia

(a. Centre of Public Experiment, b. School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to propose a multi-scale optimization design method of plate and shell damping composite structure to obtain a plate and shell structure with good anti vibration performance and ensure the normal operation of the equipment. Aiming at dynamic flexibility, a mathematical model of multi-scale problem was established under frequency domain excitation and fixed frequency point excitation. Macro distribution of damping materials and microstructure of plate and shell damping composite structure were collaboratively designed. The sensitivity of objective function and constraint conditions to design variables was derived, and the optimization mathematical model was solved based on the moving asymptote method. The proposed multi-scale design method can effectively obtain the optimal macro layout of damping materials and the optimal microstructure configuration of damping composites for plate and shell structures. It improved the structural dynamic performance. At the same time, the results also showed that the vibration response of the structure coated with damping composites was significantly reduced compared with that coated with only a single damping material. The research shows that the macro distribution of damping materials is different under different excitation frequencies. The damping materials are mainly distributed at the maximum displacement of the structural modal shape and the support end. By strengthening the structural stiffness, the structural deformation is restrained and the vibration response is reduced. The microstructure configuration is basically similar. Its basic morphology is that the distribution of low stiffness and high damping materials is strip-shaped. The strip-shaped damping composite microstructure has a large stiffness in the bending direction of the structure, which can effectively resist the bending deformation of the structure.

damping composite structures; multi-scale design; topology optimization; damping layer; harmonic load

TH113.1

A

1001-3563(2022)23-0225-09

10.19554/j.cnki.1001-3563.2022.23.027

2022–07–16

国家自然科学基金（52005337）

倪维宇（1986—），男，硕士，实验师，主要研究方向为机械结构优化与振动分析。

责任编辑：曾钰婵