假设检验及基于参数假设检验的质检算法
◎孙含笑
(石家庄铁路职业技术学院,河北 石家庄 050041)
1 引言
在实际生活中,对总体参数的研究具有极大的价值,有利于决策者作出正确的统计推断.参数研究主要包括参数的估计和检验,参数估计适用于总体分布已知但参数未知时对参数的研究.参数估计有多种方法,常见的方法有矩估计法、极大似然法、最小二乘法、贝叶斯估计法等.参数估计的研究非常广泛,并在各个领域展现出了独有的效用和价值.杨智勇等人研究了参数估计在岩土工程场地勘测中的应用,提出了考虑场地多源勘测数据三维空间相关性的土体参数概率密度函数估计方法,该研究方法为融合多源勘测数据的场地土体参数不确定性量化提供了一种有效分析工具.杨艳艳等人研究了参数估计在机器学习中的应用,提出了基于群启发式算法的机器学习参数寻优方法,该方法的参数寻优能力和效率都优于主流的网格搜索算法并且具有良好的可拓展性.李琼芳等人研究了参数估计在暴雨强度预测中的应用,高精度的暴雨强度公式是城市防洪排涝基础设施建设规划设计的重要依据.李琼芳等人提出的基于系统微分响应的暴雨强度公式参数率定方法能够快速寻找到参数真值,不仅效率高且能够避免陷入局部最优,对提升暴雨强度公式精度具有重要参考价值.
在实际应用中,对总体参数可能预先有所了解,这时会对总体参数提出假设,通过样本的信息验证提出的假设是否成立,这就是参数的假设检验.但假设检验逻辑性强,初学者很难理解其背后包含的原理以及含义.与此同时,假设检验在许多领域都有显著的价值,何宁辉等人在变压器故障诊断中引入假设检验,该模型的诊断准确性相比于传统诊断方法有较大提升.石则强等人研究了假设检验在汽车排放实验室比对中的应用研究,该研究方法能够得到比对结果的真实情况.高宇等人探讨了假设检验在生物学中的应用,以期为生物学数据的统计分析提供新的思路.乔俊峰考虑了假设检验在舰船通信网络信息安全中的应用,该加密模型相较于传统的加密模型提高了加密的安全系数.基于此,有效地降低假设检验的学习难度具有一定的意义.本文深入地分析参数假设检验,加深学习者对假设检验的理解,并通过Matlab实现基于参数假设检验的质检算法,用以保证系统和零部件的可靠性以及检验试验在不同的操作过程中是否有本质上的区别.使用该算法进行质检时,质检人员只需要输入样本数据以及选择检验类型,便可得到最终结果,这不仅降低了质检人员的使用难度,而且提升了质检的有效性.
2 假设检验
2.1 假设检验的基本思想
概率性质的反证法
假定对总体的某种假设H0是正确的,那么不支持这一假设的事件A即为小概率事件,在一次试验中几乎不可能发生,实际上可认为是不发生的.若在一次抽样试验中样本观察值导致事件A发生,与小概率不发生矛盾,则拒绝这一原假设;否则就接受原假设.
2.2 参数假设检验的主要概念
(1)原假设与备择假设
统计中常把要检验的假设称为原假设,记为H0,还需要建立一个与H0对立的假设,称为备择假设,记为H1.
(2)显著性水平
α=P{拒绝原假设H0|H0为真}是公认的小概率事件的概率值.
(3)两类错误
在假设检验的过程中,对判定原假设是否为真,即作出决策的依据仅仅是一个样本.由于样本的随机性,要进行判断就不可避免会发生错误.
①当原假设H0实际为真时,也有可能是样本观察值导致小概率事件发生,而作出拒绝H0的判断,称为第一类错误,又叫弃真错误.犯第一类错误的概率是显著性水平α.
α=P{拒绝原假设H0|H0为真.}
②当原假设H0实际为假时,样本观察值未导致小概率事件发生,而作出接受H0的判断,称为第二类错误,又叫取伪错误.其发生的概率为β.
β=P{接受原假设H0|H0为假}.


图1 两类错误关系图
只有扩大样本量n,才能使α与β同时减小.在实际中,样本量过大不现实.通常情况下,我们会控制犯第一类错误的概率,使之不超过α.原因有两点:
①通常情况下,人们认为犯第一类错误的后果更严重一些,因为犯第一类错误即错过了事实存在的真相.
②在实际计算中,犯第二类错误的概率β计算比较复杂,因此更容易控制犯第一类错误的概率.
(4)检验统计量
用于检验假设的统计量(统计量:不含未知参数的样本函数)是检验统计量.文章只考虑正态总体均值和方差的检验,选取标准如下:
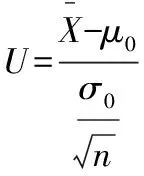
(5)拒绝域
拒绝域W1:拒绝原假设H0时,样本值观察值(x1,x2,…,xn)所构成的集合.
假设检验根据拒绝域的形式分为双边检验和单边检验,单边检验又分为左边检验和右边检验.划分标准如下:
①拒绝域在两边称为双边检验,如图2所示.备择假设表现为含有“≠”符号.
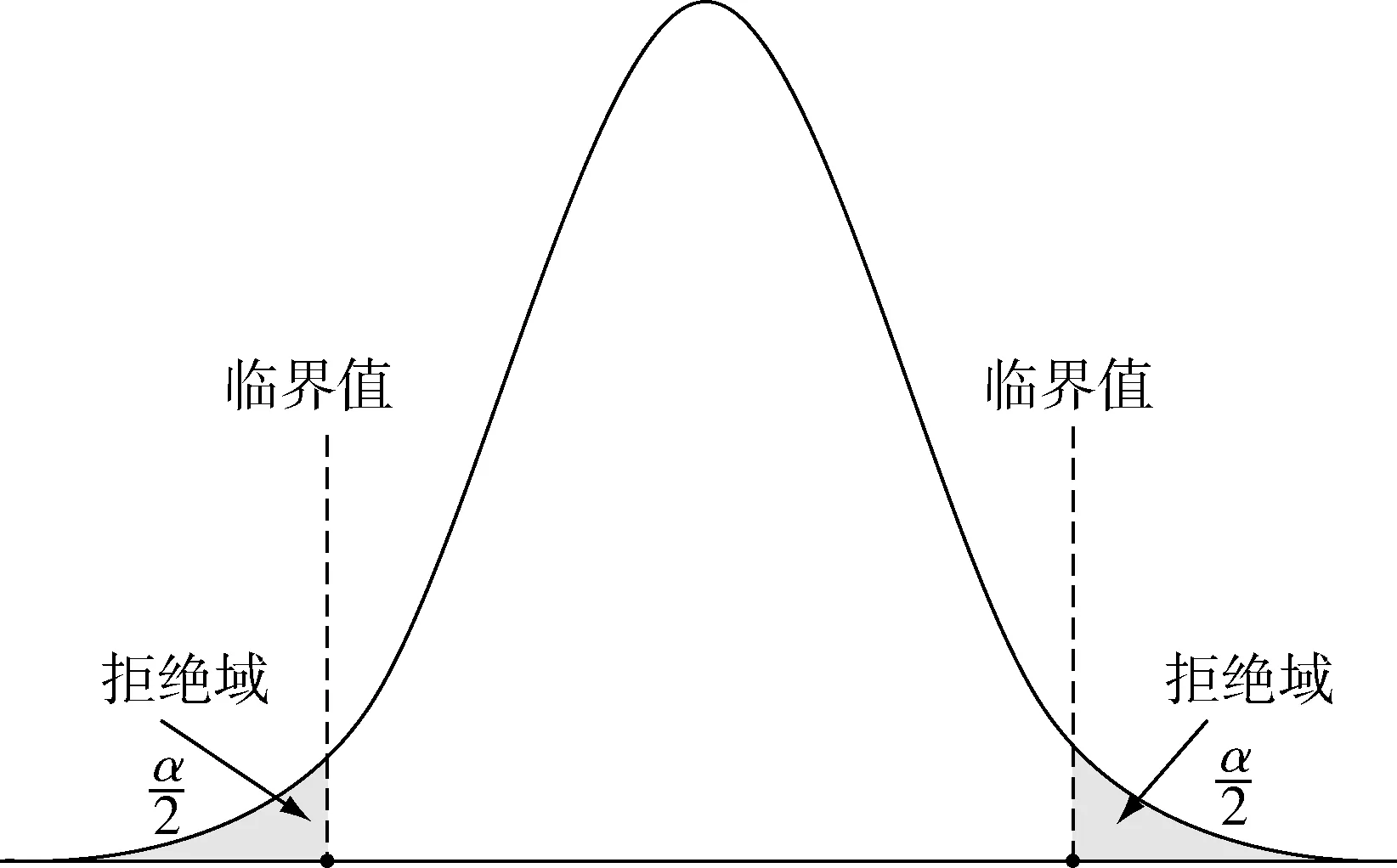
图2 双边检验拒绝域
②拒绝域在右边称为右边检验,如图3所示.备择假设表现为含有“>”符号.

图3 右边检验拒绝域
③拒绝域在左边称为左边检验,如图4所示.备择假设表现为含有“<”符号.

图4 左边检验拒绝域
2.3 假设检验的一般步骤
假设检验的一般步骤归纳如下:
(1)根据实际情况,建立两个完全对立的假设;
(2)选择合适的检验统计量;
(3)依照实际情况确定显著性水平,表述拒绝域形式;
(4)根据样本信息,对总体参数作出判断.
若样本观察值(检验统计量)落入拒绝域W1内,则拒绝原假设H0;若样本观察值(检验统计量)没有落入拒绝域W1内,则接受原假设H0.
3 基于参数假设检验的质检算法
基于假设检验的原理设计一种质检算法模型,并通过Matlab软件中相关函数实现该模型.具体思路为:根据实际需求,设定合适的显著性水平α.本文只考虑正态总体的假设检验,首先判断是单个正态总体还是两个正态总体的假设检验.如果是单个正态总体的假设检验,方差检验则需选择χ2检验法.对于均值的假设检验,则需要进一步判断方差已知还是方差未知,方差已知时选择U检验法,方差未知时选择t检验法.如果是两个正态总体的假设检验,均值检验选择t检验法,方差检验选择F检验法.然后,根据实际需求,选择左边检验、右边检验或双边检验.该算法模型适用于解决正态总体均值和方差的假设检验,具体流程如图5:
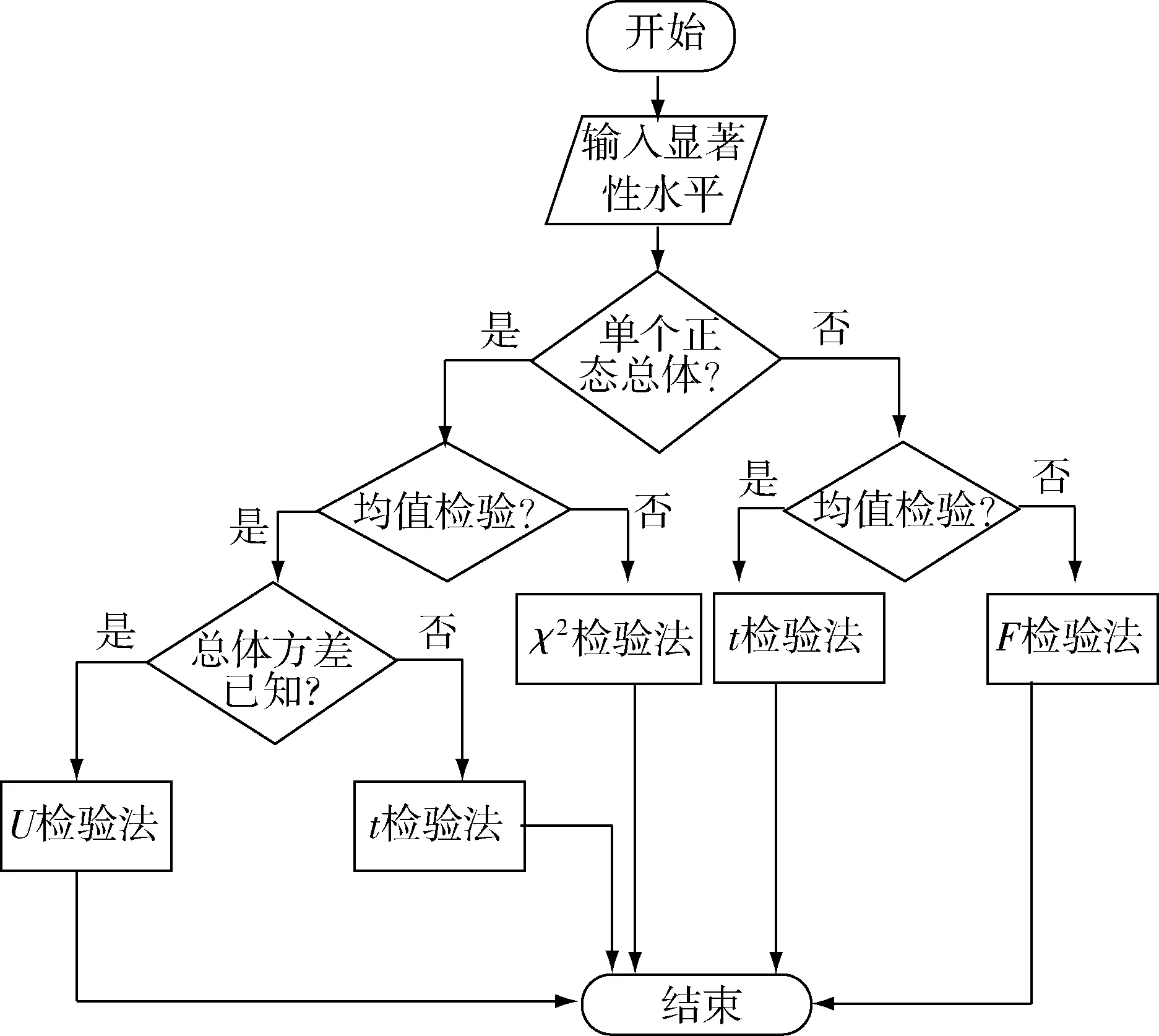
图5 算法流程图
4 算法的应用
例1[工艺改进]为了验证新的操作方法是否能提高钢的产率,在保证其他试验条件一样的情况下,分别按照标准方法和新方法炼10炉钢,其产率如下表所示:
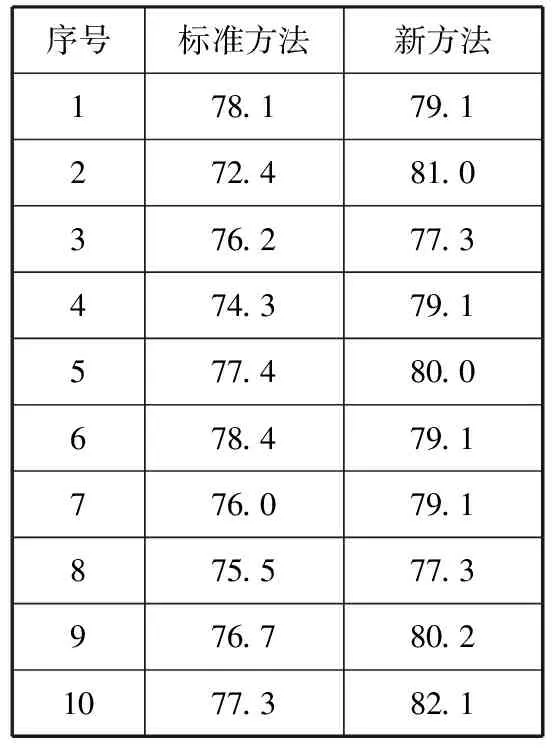
产钢量
设这两个样本是相互独立的正态总体,μ和σ2均未知.按照新的方法能否提高钢的产率(α=0.05)?
运行程序,输入必要参数,演示如下:
输入显著性水平:
0.05
单个正态总体请输入[1];两个正态总体请输入[2]:
2
对方差检验请输入[F];对均值检验请输入[J]:
J
请输入样本值:x=
[78.1,72.4,76.2,74.3,77.4,78.4,76.0,75.5,76.7,77.3]
请输入样本值:y=
[79.1,81.0,77.3,79.1,80.0,79.1,79.1,77.3,80.2,82.1]
双边检验请输入[0];右边检验请输入[1];左边检验请输入[-1]:
-1
运行结果:
在显著性水平0.05下,可以拒绝原假设H0,即μ1<μ2;
即在显著性水平0.05下,新的操作方法能提高钢的产率,其平均产钢率要高于标准方法.
例2[故障排查]当机器正常工作时,机器切割金属棒的平均长度x为10.5 cm,从中随机选取15段进行测量,金属棒的长度x如下:
10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2
10.9 10.6 10.8 10.5 10.7 10.2 10.7
已知总体X~N(10.5,0.15),该机器工作是否正常?(α=0.05)
运行程序,输入必要参数,演示如下:
输入显著性水平:
0.05
单个正态总体请输入[1];两个正态总体请输入[2]:
1
对方差检验请输入[F];对均值检验请输入[J]:
J
请输入样本值:x=[10.4,10.6,10.1,10.4,10.5,10.3,10.3,10.2,10.9,10.6,10.8,10.5,10.7,10.2,10.7]
双边检验请输入[0];右边检验请输入[1];左边检验请输入[-1]:
0
如果总体方差已知,请输入[u];如果总体方差未知,请输入[t]:
u
请输入已知的均值:
10.5
请输入正态总体的标准差:
0.15
运行结果:
在显著性水平0.05下,可以接受原假设H0,即μ=10.5.
5 结论
本文对假设检验作了深入描述和分析,能帮助学习者更好地理解假设检验.同时,基于参数假设检验的基本原理和统计推断中的常用方法,通过Matlab编程设计了工程质检算法模型,方便质检人员进行质量检测和故障排查.但本文设计的质检模型比较单一,只能用于较简单的正态总体方差和均值的检验,如何设计更为有效且精确度高的质检模型仍需进一步研究.

