构造几何图形 妙解代数问题
◎杨诗婷 马绍文
(云南师范大学,云南 昆明 650500)
一、前言
“数学思想是数学的生命,是数学的灵魂”.其中数形结合思想是解题中常用的思想,数抽象而形式化,形具体而形象化.数与形对应的思维是分析性思维和视觉化思维,这两种思维在数学解题中都是非常重要的,它们在数学解题中相互作用,互为补充.
数形结合思想一般分为两种,一种是由“形”到“数”的转换,即将几何问题转化为代数问题,将复杂的问题简单化;另一种则是由“数”到“形”的转换,将代数问题转化为几何问题,使问题变得直观易懂.构造图形解决代数问题是数形结合思想的具体应用之一,对于复杂的代数问题,构造特殊的几何图形,将问题和条件直观地展示出来,化繁为简,便于解决问题.本文将通过4个典型例题,分析妙用斜率公式、距离公式和余弦定理构造图形解决代数问题的方法.
二、妙用斜率公式

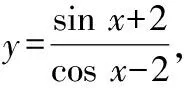

其中tanα=-y,
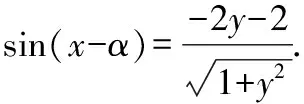
整理得3y2+8y+3≤0,
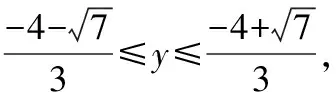

解法二
分析题中的函数可以看作点A(cosx,sinx)和点B(-2,2)所在直线的斜率,则问题就转换为求直线AB斜率的取值范围.点A(cosx,sinx)是单位圆上的任意点,点B是定点,构造图形(如图1),观察图形发现当直线AB与单位圆相切时,直线AB的斜率取最值.故求出直线AB与单位圆相切时直线AB的斜率即可解决问题.
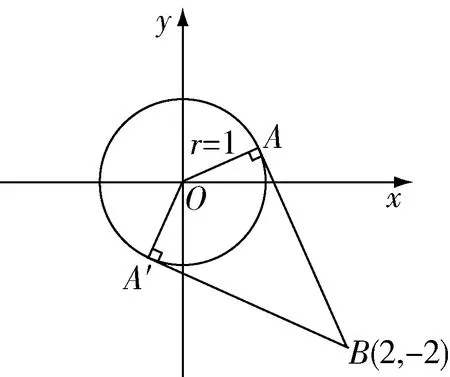
图1

如图1所示.
设直线AB的斜率为k,则直线AB的方程为kx-y-2k-2=0.
因为直线AB与单位圆相切,
所以圆心O到直线AB的距离为1,



评注:解法一用代数法解决该题,解法二则利用数形结合解决该题.二者的区别在于解法一需要将题目所给函数转换为正弦函数,利用正弦函数的性质得到不等式进行解题,而解法二则利用图形直接得到结果.所以解法二较为简便.

分析求函数值域的常用方法有单调性法、换元法和导数法,但是题目中所给的函数式是分式,所以换元后还是分式,求导也会将题目复杂化,函数的单调性也不容易判断,因此利用斜率公式构造图形来求解.其中y可以看成是点A(-2,1)与点B(x2,3x2)所在直线的斜率,则问题就转换为求直线AB斜率的取值范围.
解y可看成是点A(-2,1)与点(x2,3x2)所在直线的斜率,设x′=x2,y′=3x2,则y′=3x′(x′≥0).
故原函数的值域即为点A(-2,1)与直线y′=3x′(x′≥0)上的点(x′,y′)所在直线的斜率的取值范围.
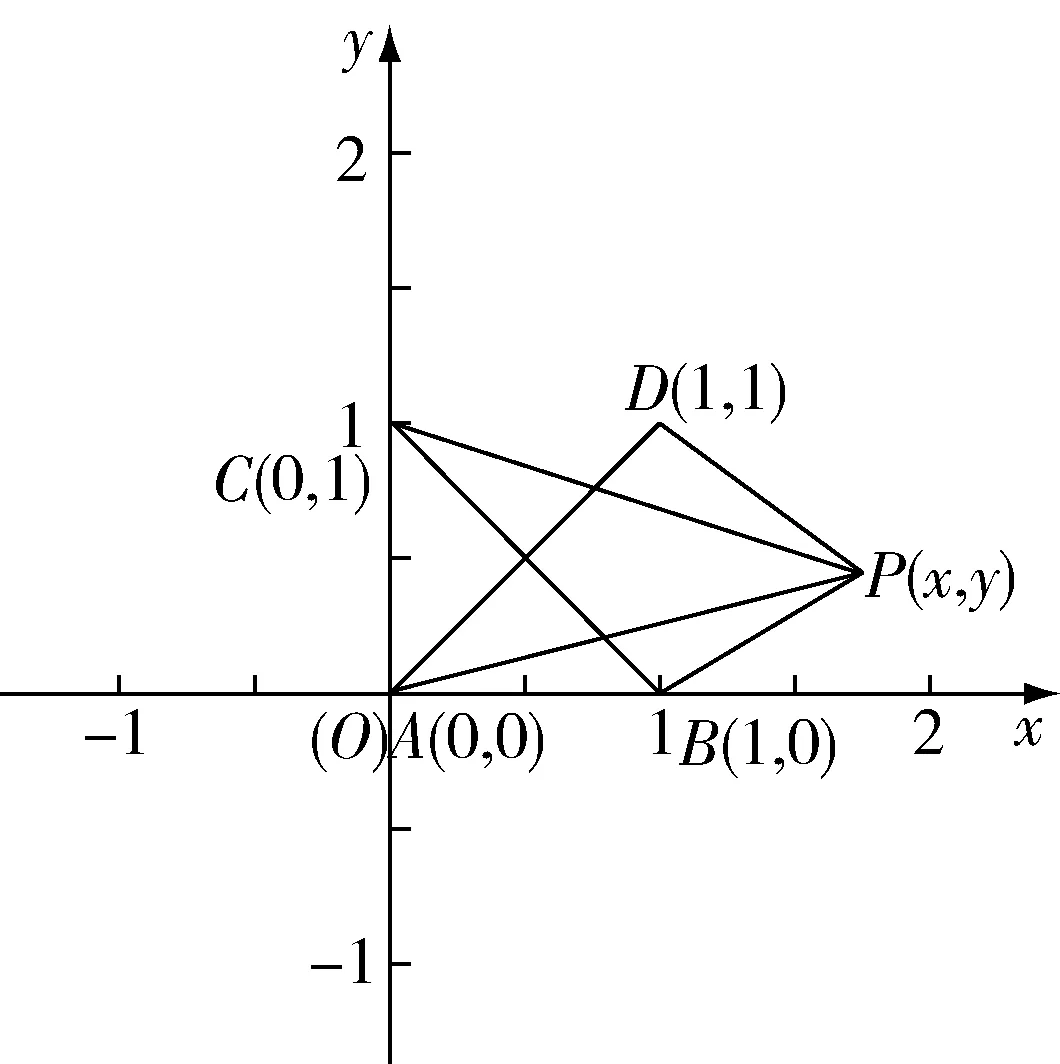
如图2,作射线AC与直线y′=3x′(x′≥0)平行,易得kOA≤y 图2 设点A(3,2),点B(0,1),点C(x,x2),如图3所示. 图3 此时问题转换为求线段AC和BC长度之差的最大值. 由图易知AC-BC≤AB, 当点C运动到点P时,AB取得最大值, 解如图4所示,f(x,y)表示在平面直角坐标系中的动点P(x,y)到定点A(0,0),B(1,0),C(0,1),D(1,1)的距离之和. 图4 在△APD中,PA+PD≥AD,当且仅当点P在AD上时等号成立, 在△CPB中,PC+PB≥BC,当且仅当点P在BC上时等号成立, 例5已知x,y∈R且x2+y2-2x-2y-2≤0,求|x+y+3|的最值. 分析题中待求的式子有绝对值并且有两个变量,用代数方法求该式时首先要去绝对值.因为有两个变量,所以考虑利用平方法去绝对值,但是转换之后式子更加复杂,所以利用代数方法解决该题较困难.观察发现题目中|x+y+3|与点到直线的距离公式相似,同时不等式可以恒等变换为(x-1)2+(y-1)2≤4,即以点A(1,1)为圆心,半径为2的圆内或圆上的任意点到直线x+y+3=0的距离,于是结合点到直线的距离和不等式的几何意义构造图形解决问题. 解x2+y2-2x-2y-2≤0可化为(x-1)2+(y-1)2≤4, 图5 如果题目中出现或者经过恒等变换后出现形如x2+y2-mxy(其中m=2cos〈x,y〉)的式子,则可以结合余弦定理a2+b2-2abcosC构造图形解决问题. 分析该题求证的结论很复杂,直接用基本不等式法求证很难.求证不等式的常规方法:先算出不等式左边的最小值,然后再算出不等式右边的最大值,最后将二者进行比较.而不等式中的式子都含有根号,这样解决会使问题复杂化,所以该问题难以用代数方法证明.观察不等式中的式子,从整体性出发,可以联想到“三角形两边之和大于第三边”,而第一个被开方数类似于勾股定理的形式,后面两个被开方数的形式则与余弦定理很相似.所以构造与题意相符的三角形来解决问题. 证明如图6,构造一个四边形ACBD,使AB,AC,AD的长分别是x,y,z,并且∠BAC=90°,∠BAD=60°. 图6 在△ABD中,由余弦定理得BD2=AB2+AD2-2AB·ADcos∠BAD=x2+z2-xz, 在△BCD中,BC+BD>CD, 当B点在CD上时,有BC+BD=CD, 图7 当B,C两点均在AD上时取等号, 通过对例题的分析和解答,可以发现利用数形结合思想解决代数问题很直观,而且容易理解,同时避免了繁杂的代数运算.但是这种方法有一定的局限性,如果图形不准确、不完整就会导致解答过程出现错误,所以在使用这种方法的过程中要注意图形的准确性和完整性.另外,通过构造图形解决代数问题时,学生需要深刻理解题目,并建立旧知与问题之间的联系.面对具体问题,学生要从不同角度去分析,这样就会使学生对问题的条件、结论以及它们之间的联系和转化方式有了多角度的理解,从而对条件、结论有不同形式的表达,形成多样化的解题方法,进而在解题时达到事半功倍的效果. 总之,数形结合是一种科学的、高效的解题方法,本文分析的“以形解数”的解题方法蕴含数形结合思想.若学生能够将数形结合思想运用到解题中,这将是对学生思维的一种开拓,会使学生在深刻理解知识的同时高效地学习.


三、妙用距离公式
(一)妙用两点间距离公式







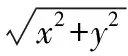


(二)妙用点到直线的距离公式




四、妙用余弦定理




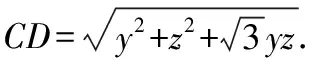

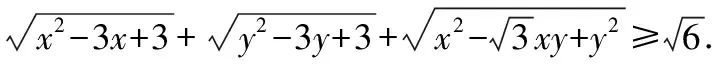

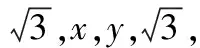





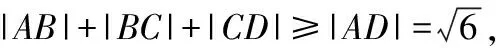
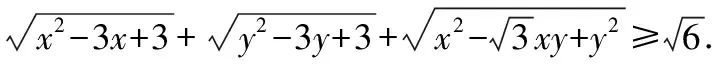
五、小结

