概率扭曲与A股市场风险定价①

石 芸， 芮 灏， 周 勇

(1. 华东师范大学统计学院和统计交叉科学研究院， 统计与数据科学前沿理论及应用教育部重点实验室, 上海 200062； 2. 上海大学管理学院， 上海 200444)

0 引 言

概率扭曲(probability distortion), 又称为概率权重(probability weighting)描述的是决策者在不确定性环境下的一种心理偏差：高估(或低估)尾部小概率事件发生的客观概率，是投资者心理偏差的一种有效度量，近年来受到国内外金融学家的重视.在金融市场中，概率扭曲首先会影响投资者对尾部风险的感知，进而影响投资者的投资决策行为，最终落在对资产均衡价格的影响.现实中，投资者会为了规避左尾风险而做出保守的投资决策，同时也会因追逐右尾收益而产生博彩行为.在概率扭曲的作用下，这两种投资行为又会受到怎样的影响？资产的风险定价是否会因之而改变？为了回答这些问题，本文将立足中国A股市场，从理论和实证两个角度来探究概率扭曲对于资产风险与收益关系的影响.

经典资本资产定价模型(CAPM)使用Beta来衡量系统性风险，并指出一个风险厌恶型的投资者自然要求“高风险高收益”，即Beta风险和收益应是正向关联的.然而，实证研究的结果却往往并非如此.Fama和French[1]的研究结果指出了Beta与预期收益率没有显著关系.Baker等[2]更进一步指出在美国市场中卖空高Beta的股票并买入低Beta的股票能获得较高的超额收益(即Beta和预期收益之间呈负向关联).这种实证结果与理论预期的不一致在文献中又称为Beta异象(Beta anomaly).Frazzini和Pedersen[3]发现Beta异象在19个发达国家股票市场普遍存在.A股市场也有很多Beta异象的相关研究.陈浪南和屈文洲[4]发现A股市场Beta与预期收益率的相关性不稳定.靳云汇和刘霖[5]指出Beta与预期收益率的关系是非线性的.陈收和曹雪平[6]将市场状态划分为牛市和熊市，发现当市场处于牛市(熊市)时，Beta与收益率正(负)相关.潘莉和徐建国[7]同时检验了Beta、市值等多个因子对于A股的回报率的影响，并发现Beta对A股市场定价没有影响.

针对Beta异象的背后原因，现有文献从不同的角度给出了解释: 市场的无效性[8], 市场摩擦[2, 9]，杠杆约束[3]，投资者情绪影响[10]，投机性需求[11]，彩票偏好[12]，以及特质波动率与Beta异象的互动关联[13]等.本文从概率扭曲的视角，为理解Beta异象提供了一个新的渠道.

为了弄清楚概率扭曲的作用，本文先从相关文献中的一些解释出发，探讨概率扭曲在Beta资产定价的影响.Bali等[12]提出的彩票偏好(lottery preferences)，认为很多投资者偏好类似于彩票的投资，从而为具有潜在高收益可能性的资产(也就是高Beta资产)付出了过高的价格，使得其预期收益下降；而低Beta资产由于受到冷落，预期收益上升，从而导致了低Beta资产能带来更好回报这一异象.Frazzini和Pedersen这篇经典文章[3]则从杠杆约束角度提出了另一种解释.他们指出，在很多市场上，加杠杆是受限的，无论是客观的交易约束，还是投资者对杠杆的主观恐惧所致.在这种情况下，为了追逐更高的收益，很多投资者会更倾向买入具有较高Beta的资产，从而推高了高Beta资产的价格.可以看出，上述文献中的两种解释，都是试图找出高Beta资产的价格高估背后的额外需求：彩票偏好或者杠杆约束.不管高Beta资产的价格高估背后的原因为何，可以预见的是当投资者低估尾部小概率事件时，Beta和收益的负向关联应该仍然存在(或者负向关联更强).而当投资者足够重视尾部风险时，可能会纠正这种风险和收益的扭曲关联(即Beta风险和收益呈CAPM预测的正向关联).

除了用传统Beta来研究风险定价外，大量学者还构建了其他风险指标讨论尾部风险定价.Ang等[14]指出相比于资产价格上涨，投资者更关心资产的下行风险，他们使用下行Beta(downside Beta，记为DBeta)来衡量资产的左侧尾部风险，并发现DBeta和预期收益呈正向关系.王志强和胡玥[15]在中国市场检验的结果发现DBeta和预期收益无直接显著关系，但在同时控制市场Beta和DBeta后得到了与Ang等[14]类似的结果.凌爱凡和谢林利[16]将投资组合的尾部风险分解为特异性尾部风险、个股的系统性尾部风险和混合尾部风险来分别分析研究.Barberis 和 Huang[17]基于前景理论提出投资者喜欢具有彩票式回报的股票，即具备正偏度的股票，因而承担了更多的特质性风险.Mitton和Vorkink[18]和郑振龙等[19]分别在美国市场和中国市场通过实证检验证明了这一想法.本文从概率扭曲的新视角，考察投资者对于尾部风险的感知强弱程度对于尾部风险定价的影响.

文献中，扩展传统期望效用理论(expected utility theory, EUT)模型以包含概率扭曲行为特征的两个最著名的理论模型为：等级依赖效用理论(rank dependent utility, RDU)[20, 21]和累计前景理论(cumulative prospect theory,CPT)[22, 23].RDU理论由Quiggin[20, 24]、 Schmeidler[25]和Abdellaoui[26]等提出并发展至今，为分析概率扭曲影响提供了直接而明确的分析框架.在RDU模型中，投资者对未来事件由最坏的结果到最好的结果进行排序，不同的结果赋予不同的决策权重(decision weight).决策权重并非事件结果客观概率分布的线性函数，而是在左尾和右尾会发生扭曲.换句话说，投资者的决策权重并不是客观发生概率而是受概率扭曲影响后的主观概率.本文选取RDU框架而不是CPT框架来研究概率扭曲的影响，是因为RDU框架可以提供更为清晰直接的分析框架来剥离出概率扭曲的作用.RDU模型可以看为传统EUT模型仅仅添加了概率扭曲这一额外行为特征；而CPT框架除了概率扭曲之外还有许多其他行为特征(比如，损失厌恶， 参考点依赖等).这些额外行为特征的加入一方面使得模型复杂化，另一方面可能与概率扭曲复合形成叠加影响，难以清晰剥离出概率扭曲的单独作用.

相比于传统EUT模型中效用函数中蕴含的风险厌恶态度，概率扭曲为本文提供了多一层渠道，即投资者对于尾部风险的感知强弱程度，来重新审视A股市场的风险和收益关系.在RDU框架下，均衡定价核由边际效用函数与概率权重函数的一阶导数的乘积共同决定.也就是说，概率扭曲所描述的投资者对于(尾部)风险的感知变化会最终通过其一阶导数的形式落在对均衡定价核的影响上.因此，本研究的实证工作也分为两步：

首先，通过A股市场的期权数据估计出经验定价核(empirical pricing kernel)；第二步，通过定价核和概率扭曲函数的关系反推出概率扭曲指标，最后以此指标来观察投资者对于尾部风险的主观偏好的变化，进而考察概率扭曲对于定价的影响.通过理论推导和实证检验，首先发现A股市场经验定价核具备时变特征(time-varying)：当代表性投资者高估尾部事件时，经验定价核呈U形；而当投资者低估尾部事件时，经验定价核则呈现钟形.关于经验定价核的形状，国内外都有大量的文献对此研究讨论.早期Singleton[27]使用了宏观的总消费数据来估计定价核，但是宏观数据的测量有较大的误差，因此这样估计出来的定价核并不准确.Ait-Sahalia和Lo[28, 29]使用了美国标普500期权数据来估计定价核.吴鑫育[30]使用了恒生指数期权来估计了港股市场的定价核，并发现港股的经验定价核形状为驼峰(钟形).赵凯[31]使用了中国波动率指数(IVIX)数据作为上证50ETF 期权的代理指标，通过联合极大似然估计得到A股市场的经验定价核，指出经验定价核为单调递减.相较于国外研究，中国A股的期权发展时间并不长，关于A股定价核的文献较少，本文在这方面也提供了有益的发现.

本研究设计如下，首先，通过推导出RDU框架下的CAPM模型，从理论上分析概率扭曲对于系统性风险的定价影响.传统CAPM模型假定代表性投资者是风险厌恶的，因此承担高风险必然要求高回报，即风险和收益之间应为正向关联.相比于传统模型中的风险厌恶，概率扭曲为本文提供了多一层渠道，即投资者对于尾部风险的感知强弱程度，来额外影响风险和收益的关系.然后，使用上证50ETF期权的数据估计得到2015年～2018年期间(周频)经验定价核的形状，对A股市场的概率扭曲时变特征有个初步了解.紧接着，构造多个概率扭曲指标来将市场状态分为高估和低估的状态，并使用一元投资组合排序法(one-way sort)，Fama-MacBeth回归和面板回归检验了系统性风险Beta(DBeta)与股票的预期收益率之间关系.最后，检验概率扭曲对于代表特质性风险的特质波动率的定价影响.综合本研究发现：当市场处于低估尾部时期，不管是系统性风险还是特质风险，都与预期收益显著负相关；而在高估时期，系统性风险和特质风险都与预期收益显著正相关.

本文的研究是对文献中已有A股市场的风险定价研究的一个补充，并且为理解A股市场的风险定价提供了一个崭新的视角.

1 理论模型与样本数据

1.1 概率扭曲下的CAPM模型

本节主要从理论角度来讨论概率扭曲对于系统性风险的定价影响.从Cochrane[32]经典的定价公式出发，考虑具备CRRA(相对风险厌恶不变)效用函数的代表性投资者，具体定价公式为

E[Ri]-Rf=-RfCov(Ri,mCRRA)

(1)

任意资产的超额回报由该资产的回报和定价核mCRRA的协方差共同决定，而CRRA投资者的定价核mCRRA受效用函数的一阶导函数u′(RM)影响.考虑概率扭曲的影响，投资者效用函数替换为符合RDU偏好的效用函数，上式的定价核mCRRA则相应地替换为mRDU，定价公式为

E[Ri]-Rf=-RfCov(Ri,mRDU)

(2)

Xia和Zhou[33]指出，在RDU框架下的定价核,mRDU的形状由效用函数的一阶导函数和概率扭曲函数的一阶导函数共同决定，具体形式为

mRDU=λ-1w′(FRM(RM))u′(RM)

(3)

其中λ=(1+rf)E[w′(FRM(RM))u′(RM)]是一个常数，RM为市场组合的回报，FRM(RM)为市场组合的回报的累计概率分布函数(CDF)，w(p)为概率扭曲函数.比较式(1)和式(2)不难看出，传统的期望效用理论中，能够影响投资者权衡风险和收益关系的是效用函数中蕴含的风险厌恶程度(凹型的效用函数就代表了风险厌恶型投资者).而RDU框架下的概率扭曲函数为本文提供了多一层渠道，即投资者对于尾部风险的感知强弱程度，来分析投资者如何权衡风险和收益关系.换句话来说，在RDU框架下，不仅风险厌恶程度(边际效用函数)会影响投资者权衡风险和收益关系，投资者的风险感知强弱程度(概率扭曲强弱)也会产生叠加影响.后面的理论和实证分析都表明投资者对尾部风险的低估甚至会扭曲原本效用函数中蕴含的风险厌恶态度表现为风险喜好行为，从而扭曲市场的风险和收益的定价关系.

关于概率扭曲函数w(p)的函数形式，文献中有很多(比如Tversky 和 Kahneman[23]，Lopes[34]).为后面实证方便起见，选取Prelec[35]提出的单参数函数形式(1)本文为方便起见选用Prelec[35]提出的单参数函数形式代表概率扭曲函数，实际上如果选用其他文献中常用的概率扭曲函数，比如Tversky和Kahneman[23]提出的双参数函数，并不会影响本文的主体结论.为节约篇幅，只给出了Prelec概率扭曲函数下的结果.

w(p)=exp(-(-ln(p))α)

(4)

其中p为客观概率，α为概率扭曲参数，其控制了概率扭曲函数的形状.当α>1时，概率扭曲函数w(p)的形状为S型(S-shape)，意味着投资者低估尾部小概率事件；当α<1时，概率扭曲函数w(p)的形状为反S型(inverse S-shape)，即投资者高估尾部小概率事件.

当概率扭曲函数形状变化时，对应的定价核mRDU形状也会随之而变化，相依关系见式(3).在设定市场回报率符合A股市场情况和选用幂效用函数下，图1为定价核与市场收益的关系图.(2)绘制定价核需要先假设市场收益分布，吴鑫育等[36]指出上证50ETF收益率存在明显的偏度和尖峰厚尾特征，因此假定市场收益服从偏正态分布(Skew-normal distribution).本文对2005年1月～2018年12月的上证50ETF的日频数据进行估计，将市场组合分布参数具体设定为相应估计值：均值为0.096，波动率为0.20，偏度为0.03(年化后的数值)的偏正态分布，无风险利率设为0.04.效用函数为CRRA(常相对风险规避效用函数)，其中风险系数为γ = 2.当α=1时(即不考虑概率扭曲)，定价核退化为传统模型结果，只依赖于效用函数的一阶导函数，因此呈微向下倾斜直线(图中实线).当α<1时，投资者高估尾部小概率事件，对两个尾部都愿意支付更高的价格，从而产生一个U形的定价核(图1中长点虚线).当α>1时，投资者低估尾部小概率事件，定价核形状变为钟形曲线(Bell shape，图1中短点虚线).

图1 不同概率扭曲水平下的定价核

定义函数m(x)=λ-1w′(FRM(x))u′(x)，可以将RDU定价核看成是RM的函数,并在RM=1这一点进行一阶泰勒展开

mRDU=m(1)+m′(1)(RM-1)

=λ-1w′(FRM(1))u′(1)+λ-1×

[w′(FRM(1))u″(1)+w″(FRM(1))×

u′(1)FRM(1)](RM-1)

(5)

将式(5)代入Cochrane定价式(2)可得RDU-CAPM

E[Ri]=Rf+ACov(Ri,RM)

(6)

其中

A=-1E[w′(FRM(RM))u′(RM)]×

[w′(FRM(1))u″(1)+w″(FRM(1))×

u′(1)FRM(1)]

(7)

表达式(6)就是考虑了概率扭曲的RDU-CAPM定价公式, 系数A代表着市场风险的风险溢价水平.当不考虑概率扭曲，RDU-CAPM退化为经典CAPM模型，其中系数A退化为

A=-u″(1)E[u′(RM)]

(8)

经典CAPM模型下，CRRA型投资者风险厌恶(凹性效用函数)，因此风险溢价系数A取值为正.比较式(7)和式(8)不难发现，在RDU框架下，市场风险的风险溢价水平不仅会受到市场状况和代表性投资者风险厌恶程度的影响，还会受到概率扭曲水平的影响.正是添加的概率扭曲函数，在风险厌恶水平之外，为本文提供了多一种渠道来分析(主观)风险与收益之间的联系，即投资者对于尾部风险的感知强弱程度会影响投资者权衡风险和收益.

经典CAPM模型，市场风险溢价系数A取值为正，代表着“高风险高收益”：一个理性的风险厌恶型投资者承担风险，自然要求正的预期回报.然而经典CAPM模型在实证检验中常常遇到困难，高风险未必对应高回报(Beta异象).而在本文的模型中，考虑了概率扭曲的影响，风险溢价系数A的符号理论上可正可负，取决于投资者对于尾部风险的感知强弱程度.后面的仿真实验(图2)和A股市场的实证检验都表明：当投资者高估(低估)尾部风险时，系数A为正(负).如果不考虑概率扭曲的影响，直接去检验CAPM模型，那么市场高估时期的正向关联和低估时期的负向关联，正负相抵，往往得出的结论就如前人实证发现的A系数不显著(参见Fama和French[1]美股市场结果及潘莉和徐建国[7]A股市场结果).通过添加概率扭曲的影响，本文的模型为理解认知Beta异象提供了崭新视角.

图2 不同概率扭曲水平α参数下的风险溢价系数A

在利用实际数据检验A的符号之前，不妨先用仿真作图考察不同概率扭曲水平对于风险溢价水平的影响.在设定市场回报率符合A股市场和选用幂效用函数下(参数设定与图1一致)，图2所示为不同α参数下对应的A的变化.由图2可见，当α<1时，投资者高估尾部小概率事件(关于尾部风险的感知比较强)，此时风险溢价系数A为正，即投资者对于高风险的资产要求高回报.当α>1时，投资者低估尾部小概率事件(关于尾部风险的感知比较弱)，此时风险溢价系数A由正转负.这意味着低估尾部风险甚至会扭曲投资者原本的风险厌恶态度，呈现出风险喜好行为，从而扭曲风险和预期回报之间的关系.这是在等级依赖效用理论(RDU)框架下的新发现，背后的主要因素是概率扭曲水平α的变化会影响投资者对尾部风险的感知，从而影响尾部风险的定价.之后的实证研究将会围绕本节的理论结论进行相应的实证检验.

1.2 变量的定义与计算方式

使用Beta作为系统性风险的代理变量，使用DBeta作为左尾风险的代理变量，同时考虑了特质波动率作为特质性风险的代表.为了实证结果更具稳健性，在回归中加入了文献中常用的4个控制变量：市值因子、反转因子、动量因子和账面市值比因子.这些因子的具体计算方式如下.

1.2.1 系统性风险的计量

使用180天日频数据滚动回归来计算Beta，然后将每周最后一个交易日的Beta作为当周的Beta.具体的回归形式如下

ri,t=αi+βirm,t+εi,t,∀t∈T

(9)

其中ri,t为股票i在t日的收益率；rm,t为第t日的市场组合收益率，这里的市场组合收益率使用了等权的计算方式，αi和εi,t分别为回归的常数和残差.(3)实证中计算市场组合收益率常用等权和市值加权两种方式.两种计算方式并不影响本文的主体结论，出于篇幅考虑，本文只汇报了等权结果，读者如感兴趣市值加权下的结果可以联系作者索取.

也有学者如Ang等[14]提出使用下行Beta(DBeta)计量左尾风险.因为真实世界中的投资者一般更关注资产的下跌，使用DBeta可以更好地刻画投资者这种心理.同样使用180天日频数据滚动回归来计算DBeta，具体计算如下

ri,t=α-i+β-irm,t+ε-i,t,当rm,t≤rm-σrm

(10)

计算DBeta选取了市场收益率低于180天平均收益r-m减去一个方差σrm的那些样本，因此在对应的Beta回归参数上加上了上标负号以示区分，其余与估计Beta时相同.

1.2.2 特质波动率的计算

Liu等[13]的研究发现，特质波动率与Beta存在显著的正相关(美股数据二者的相关系数达0.33).而前面的理论分析已经表明概率扭曲对于Beta风险定价的影响，那么概率扭曲对于特质波动率的定价可能也存在影响.另一方面，具备高特质波动率的股票往往更容易发生尾部极端回报(而尾部正是概率扭曲起作用的地方)，因此从这个角度出发，概率扭曲也可能对于特质波动率的定价产生影响.然而，由于特质波动率代表了非系统性风险，不能像前面分析Beta风险那样，先从理论上推导RDU-CAPM，分离出概率扭曲对其影响，然后再用实证数据检验理论得到的结果是否成立.因此，拟在后文的Fama-MacBeth回归中直接加入特质波动率，从实证的角度分析概率扭曲对于特质波动率定价的可能影响.

通过对Fama-French三因子进行OLS日频数据滚动回归的方式来提取特质波动率，回归的窗口期同样为180天，具体的回归公式如下

ri,t=αi+βiMKTMKTt+βiSMBSMBt+

βiHMLHMLt+εi,t

(11)

其中ri,t为股票i在t日的超额收益率，MKTt为t日的市场收益率，SMBt为市值因子，HMLt为价值因子，βiMKT、βiSMB和βiHML分别代表了3个因子的回归系数.εi,t为股票i在t日的回归残差.在求得回归残差后按式(12)计算特质波动率(IV)

IV=∑nj=1ε2i,jn-4

(12)

1.2.3 变量标识与说明

表1总结了本文所使用的变量符号及计算说明.

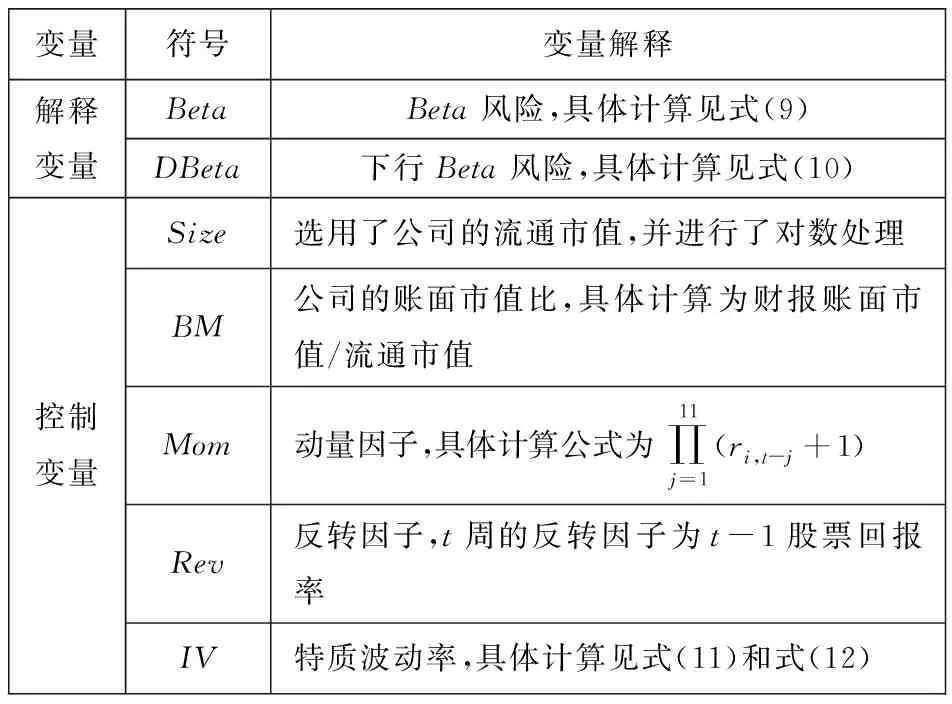
表1 变量定义

1.3 数据来源

本文所使用的股票、Fama-French三因子和上证50ETF期权的数据来源于国泰安数据库，所选择的数据时长为从2015年2月1日～2018年12月31日，实际交易周数为171周.股票数据选取了A股包含ST和创业板的所有股票数据，为了避免新股发行数据造成扰动，剔除了上市时间过短(6个月之内)的股票数据，筛选后共有3 039只股票数据.本文的波动率指数(IVIX)的数据来源于Wind数据库，时间跨度为2015年2月9日～2018年2月18日.由于IVIX数据跨度比其他数据要短，因此下面的实证分析分别针对两个时间段进行检验.用“全样本”标记时间跨度为2015年3月1日～2018年12月31日的长数据段(扣除缺失数据后一共169周).用“IVIX-样本”来标记时间跨度为2015年2月9日～2018年2月18日的短数据段(扣除缺失数据后一共有158周).

2 实证研究与结果分析

2.1 经验定价核和概率扭曲函数的估计

首先使用上证50ETF期权和上证50ETF的数据，参照Bliss 和Panigirtzoglou[37]和 Kostakis等[38]所提出的非参数方法，估计得到上证50ETF周收益率在风险中性世界的概率分布函数Q(x)和概率密度函数q(x).

参照Polkovnichenko和Zhao[39]以及吴鑫育[30]等的做法，对上证50ETF的日收盘数据建立如下的EGARCH(1,1)模型

{ln(StSt-1)=μ+htet

ln(ht)=ω+θ1et-1+θ2[|et-1|-E(|et-1|)]+

φ1ln(ht-1)

(13)

其中St是t时刻上证50ETF的收盘价，μ为上证50ETF收益率的条件均值，ht为上证50ETF收益率的条件方差，et为独立同分布标准正态随机变量，E(|et-1|)=2/π.在选用了过去500天日收盘价估计得到EGARCH模型的参数后，模拟20 000条上证50ETF收益率在一个星期内的样本路径，进而得到上证50ETF周收益率的经验概率分布，即客观世界的概率分布函数P(x)和概率密度函数p(x).(4)作者尝试过用过去300天、400天，以及增大模拟路径数，并不影响本文主体实证结果.

下面根据定价核的定义，可以求出每个时间点的定价核m(x).具体计算公式如下

m(x)=q(x)p(x)ρ

(14)

其中ρ为一个星期的无风险贴现因子.最后，利用Polkovnichenko和Zhao[39]所提出的非参数估计方法得到了概率扭曲函数w(P0).具体计算公式如下

w(P0)=c[Q(R0)u′(R0)+∫R00Q(R)u″(R0)u′(R0)2dR

(15)

其中常数c=(∫∞0(q(R)/u′(R))dR)-1,u′(R)和u″(R)为相对风险厌恶系数为2的CRRA的效用函数的一阶导数和二阶导数，R0为上证50ETF客观概率分布的P0分位点，即P(R0)=P0.

首先，选取两个代表性的例子来展示定价核和概率扭曲函数的估计结果.图3为2018年4月第一周的结果，定价核为U形，对应概率扭曲函数呈反S形(高估小概率).图4为2016年3月第一周的结果，定价核为钟形，对应概率扭曲函数呈S形(低估小概率).对2015年2月～2018年12月期间的周频定价核和周频概率扭曲函数进行了统计，发现在总计169周的估计结果中钟形定价核(S形概率扭曲函数)和U形定价核(反S形概率扭曲函数)的比例约为2 ∶1.这一结果表明A股市场大部分时间处于低估尾部状态，这与Polkovnichenko和Zhao[39]的美国市场的结果恰好相反.

图3 2018年4月第一周的定价核和概率扭曲函数w(p)

图4 2016年3月第一周的定价核和概率扭曲函数w(p)

A股市场低估状态占主导这一结果是符合大众对于A股市场印象的.众所周知，A股市场中存在着大量的个人投资者，这些投资者并没有受到很好的风险教育，对于风险感知很容易受到了概率扭曲的作用和影响，为了追求高回报常常处于低估风险(尤其是低估小概率极端损失事件)的状态.基于中国市场的低估状态占主导这一现象，本文尝试着检验概率扭曲对于风险因子的定价影响.

2.2 概率扭曲指标构建

在估计得到A股市场的经验定价核和概率扭曲函数之后，本文进一步构造了一些概率扭曲指标在时序上将概率扭曲强弱程度区分开.具体地，通过构建的概率扭曲指标将市场区分为高估尾部时期和低估尾部时期，然后可以进一步分析风险定价在这两个时期的差异性.如果，实证结果确实证明风险因子的定价在这两个时期存在显著差异性，那么也就证明了前面的理论发现是有数据支撑的：高估时期，风险和收益关系为传统CAPM模型所预测的正向关联；而低估时期，投资者因为低估尾部风险而扭曲风险和收益的关系为负向关联.

2.2.1 概率扭曲指标(PW)

假设概率扭曲函数符合Prelec单参数函数形式(见式(4))，基于上文从期权数据得到的非参数概率扭曲函数，可以以平方误差最小的方式反拟合得到Prelec概率扭曲函数的参数α.为了方便标记高估时期和低估时期，设定概率扭曲指标PW=1/α.这样构建PW指标的好处是，PW值越大，投资者越倾向于高估尾部.具体地，当PW>1时，投资者高估尾部风险，反之，则意味着投资者低估尾部风险.这样，每一周都可以计算一个概率扭曲指标PWt，并利用这个指标是否大于(小于)1可以标记下一个星期(t+1)为高估(低估)时期.(5)利用是否大于(小于)1来标记高估和低估，低估样本数为111，高估样本数为58.为了更好的平衡高估/低估样本数，文献中另一个合理的方式是用中位数标记下一个星期为高估/低估时期.本文也做了这样的尝试，发现并不会影响这里呈现的主要结论.

2.2.2 左尾指标和右尾指标(LS&RS)

上述PW指标度量的是市场整体的概率扭曲程度，同时包含了投资者对左尾和右尾的看法.为了区别投资者对于左、右尾的看法，本文参考Polkovnichenko等[40]所提出的方法使用上证50ETF数据构造两个概率扭曲尾部指标，以区别投资者对于左、右尾的看法.Left slope(后文简写为LS)为损失状态的客观累计概率与对应的风险中性累计概率之比.Right slope(后文简写为RS)为收益状态的客观累计概率与对应的风险中性累计概率之比.具体的计算公式如下

LS=∫P00m(P)dPP0=Q0P0

(16)

RS=∫1P0m(P)dP1-P0=1-Q01-P0

(17)

其中P0为低于损益状态分割点R0的客观累计概率，即P(R0)=P0，Q0为低于损益状态R0的风险中性累计概率，即Q(R0)=Q0.针对RS，选取R0=1.01，即1%的净回报率.针对LS，选取R0=0.99，即-1%的净回报率.这两个比率可以理解为投资者愿意为一些概率事件所支付的平均价格.左尾指标(LS)越大意味着投资者高估左尾小概率事件导致对于左尾风险的风险厌恶程度越大，那么愿意支付的价格也相应地越高；而右尾指标(RS)越大则意味着投资者高估右尾小概率事件导致对于潜在上行幅度的偏好程度越大，那么愿意支付的价格也相应地越高.对于投机气氛浓厚的A股市场，本文预期RS指标作用会比较明显.此外，使用这两个尾部指标的另外一个好处是并不需要对于概率函数形式进行任何假设.基于这两个尾部指标(LS，RS)是否在中位线之上同样可以标记下一个星期为高估/低估时期.

2.2.3 波动率指数(IVIX)

本文同时也使用波动率指数IVIX作为概率扭曲指标.波动率指数，常被称作“恐慌指数”.波动率指数越高，在一定程度上反映了市场中投资者对于未知极端事件恐慌程度越高，因此可以用来衡量投资者对左侧尾部风险的风险感知.A股市场的波动率指数(IVIX)是上海交易所采用方差互换原理基于上证50ETF的数据计算而得的数据.该指数正式发布于2015年6月26日，于2018年2月22日停止发布.本文使用了每周最后一天的IVIX指数收盘价标记下一个周为高估或者低估状态.预期高IVIX代表的恐慌情绪之下，投资者更容易高估小概率事件，即标记中位线之上为高估时期，反之为低估时期.

2.2.4 概率扭曲指标间的相关性分析

在构造上述4个指标之后，下面首先对于构造的指标进行相关性分析.由表2的相关系数可知，各个指标的相关性很强.(6)由于IVIX指标时间跨度较短，因此在计算变量与IVIX相关系数时，选用了2015年3月～2018年2月较短时间跨度的数据.其余指标计算时段选用了2015年3月～2018年12月的数据.其中，IVIX和PW的相关性最强，达0.71.图5为4个指标的时序图，可以看出4个指标的联动性也很强，在市场大幅波动的时候(如2015年6月和2018年1月)，各指标均达到峰值，反映了市场此时处于高估小概率时期.此外，图中的PW、LS和RS存在的缺失点是受当期的期权的数量限制，无法计算出对应的概率扭曲指标.(本文所选取的时间段包含203个自然交易周，一共缺失了34个点，缺失率约16%).

表2 4个概率扭曲指标相关系数矩阵

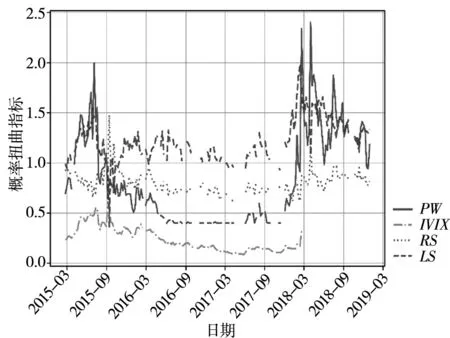
图5 4个概率扭曲指标时序图

2.2.5 概率扭曲指标的直观理解

概率扭曲指标刻画了投资者对于尾部风险的敏感程度，对于理解A股市场的尾部风险定价有非常重要的作用.这一节将本文构建的概率扭曲指标与金融市场中的一些常见指标进行相关性分析，以帮助读者更好地理解概率扭曲指标背后的经济含义.

为此选取了两个情绪指标：分析师情绪指标Analys和投资者情绪指标CICSI；两个市场状况指标：市场流动性指标Liquidity和市场波动率MarketV；以及两类尾部极值指标：时序极值MAX/MIN和截面分位数指标Q1和Q99.其中，流动性指标Liquidity和情绪指标CICSI来源于国泰安数据库.投资者情绪指标CICSI为月频数据，为了对齐本文的周频数据进行了插值处理.Analys为每周市场平均研报数作为市场分析师情绪的代表.时序极值指标MAX/MIN的计算方式为先计算个股回报每周的最大值和最小值，然后等权平均得到MAX/MIN市场指标.A股市场所有个股的周回报构成一个截面分布，Q1和Q99分别对应该截面分布的1%和99%分位点，用来刻画截面层面的市场极值事件.

上述指标与概率扭曲指标的相关系数矩阵见表3.由表3可知，与概率扭曲指标PW相关性最高的是流动性指标，达0.47；其次是代表市场波动和极值表现的指标，Q1，MIN和市场波动率MarketV.投资者情绪指标与概率扭曲指标弱负相关，这也是与直观相符的：投资者情绪倾向于衡量市场上涨的热度，而概率扭曲指标更倾向于刻画投资者对于左尾风险的敏感程度.图6进一步直观呈现了上述指标与概率扭曲指标的时序图.如图所示，流动性(Liquidity)、市场波动率MarketV和尾部极值指标(MIN)与PW指标在峰值时的变动基本一致，与分析师情绪指标的变动相关较低.

图6 概率扭曲指标与其他指标时序图

表3 概率扭曲指标与其他指标的相关系数矩阵

综上所述，概率扭曲指标设计之初是为了刻画投资者对于尾部风险的敏感程度，那么当市场处于高波动时期(往往对应尾部极值事件多发，流动性较差时期)，注意力驱动(attention driven)

的投资者往往对于风险更加敏感，能更加审慎地评估风险，承担风险要求正的风险补偿.反之，投资者对于尾部风险的忽略会导致风险与收益之前呈负向关联.这也是本文理论和实证的主体结论—高估(低估)尾部时期，风险正向(负向)定价—的心理学基础.

2.3 概率扭曲对于系统性风险定价的影响

前面定价核分析的结果显示A股市场大部分时间处于低估状态，那么这样的状态对于市场系统性风险定价的影响究竟如何？为了回答这一问题，本文首先用单变量投资组合排序法来直观地呈现风险与收益之间的关系，然后运用Fama-MacBeth回归和面板回归考察概率扭曲对风险定价的影响.

2.3.1 单变量分组排序结果

首先使用之前所构造概率扭曲指标PW、LS、RS和IVIX将市场状态分为高估和低估两个状态，然后分别在两个市场状态下做对应的单变量分组排序.以Beta风险为例，首先用Beta对A股市场全部股票排序，分为10组，然后分组计算组内平均预期回报率.P1代表Beta最小的那一组，P10代表Beta最大的那一组，P10-P1表示Beta最高的组合和Beta最低的组合的平均预期收益之差，T值检验了P10-P1的差值是否显著不为0.

表4为Beta单变量投资组合排序结果.表4结果表明，当投资者高估尾部风险时，Beta风险与收益显著正相关；当投资者低估尾部风险时，Beta风险与收益显著负相关.但是，如果不用概率扭曲指标分离出两种时期的风险态度转变，全样本时期的Beta风险与收益没有显著关系(这一结论与潘莉和徐建国[7]所检验的结果一致).右尾指标RS和波动率指数IVIX作为概率扭曲指标可以有统计上显著的区分结果，比如在IVIX指标之下的高估尾部风险时期，Beta值最高的组(P10)比Beta值最低的组(P1)有显著的1.397 7%的超额周频收益.图7对应为表4中RS指标的结果，图中实线为全样本状态下Beta风险与收益关系，虚线为低估状态，点虚线为高估状态.可以直观地看出：Beta风险和收益在低估时呈负向关联，而在高估时期呈显著的正向关系.PW虽然在趋势上显示出：高估(低估)尾部时期，随着Beta值增大，预期回报有增大(减小)趋势，但是并没有得到统计上显著的区分结果.这背后的原因可能来源于PW指标的构建方法.首先假定概率扭曲函数具备某种特殊函数形式，再通过反拟合得出单个参数代表概率扭曲的强弱程度，这一过程(虽然直观上更容易理解，但也容易造成模型误判的风险)可能损失过多信息.同样地使用期权信息，RS指标和IVIX指标因为都不需要指定概率函数的特殊形式，反而能得到比较稳健的结果.这也从侧面说明了本文从同一个信息源构建多个概率扭曲指标的必要性.LS指标的作用不太理想，这也与本文的预期一致，因此在后文回归中不再考虑LS指标的作用.

表4 Beta单变量排序结果

表5为DBeta单变量投资组合排序结果.与Beta结果一致，当投资者高估尾部风险时，DBeta风险与收益显著正相关；当投资者低估尾部风险时，DBeta风险与收益显著负相关.值得指出的是，相比于Beta，DBeta作为更直接刻画尾部下行风险的指标，概率扭曲对于其作用更明显，体现为表5中更多的显著正向/负向关系.在RS、PW和IVIX指标低估时，DBeta最高的组(P10)和DBeta最低的组(P1)的差值显著为负，t值分别为-1.90、-2.40、-2.88和-2.02；而在PW指标高估时期，P10组和P1组差值显著为正，t值为2.022 4.综上，单变量投资组合排序的结果表明当市场处于低估状态的时候，Beta(DBeta)风险与收益为负向关系，而当市场处于高估状态的时候，Beta(DBeta)风险与收益为正向关系，这与本文的理论结果相一致.

表5 DBeta单变量排序结果

2.3.2 Fama-MacBeth回归结果

通过单变量分组排序的方法，本文对于概率扭曲对Beta(DBeta)风险的定价作用有了一个初步直观的了解，但大量的文献结果表明影响收益率的并不只是Beta因子这一个变量，众所周知的市值、动量、反转等因子同样也会影响股票的收益率.加入这些常见因子作为控制变量之后，概率扭曲对于股票收益率与风险之间的关系是否还有显著的影响？本节使用Fama-MacBeth回归来回答这一问题.

同样地，分别在高估/低估状态下进行Fama-MacBeth回归，并且加入文献常用的影响收益率的动量和反转、市值因子和账面市值比作为控制变量.由于金融数据存在序列相关性，还对检验产生的t值进行了Newey-West[41]的调整，表格中的括号部分为调整后的t值.由于IVIX指数数据交易所只发布至2018年2月，而其他指标都可以计算至2018年12月，两者的时间跨度不同，因此在图7中的全样本分别包含了全样本和IVIX-样本两个数据时段作为对照分析.

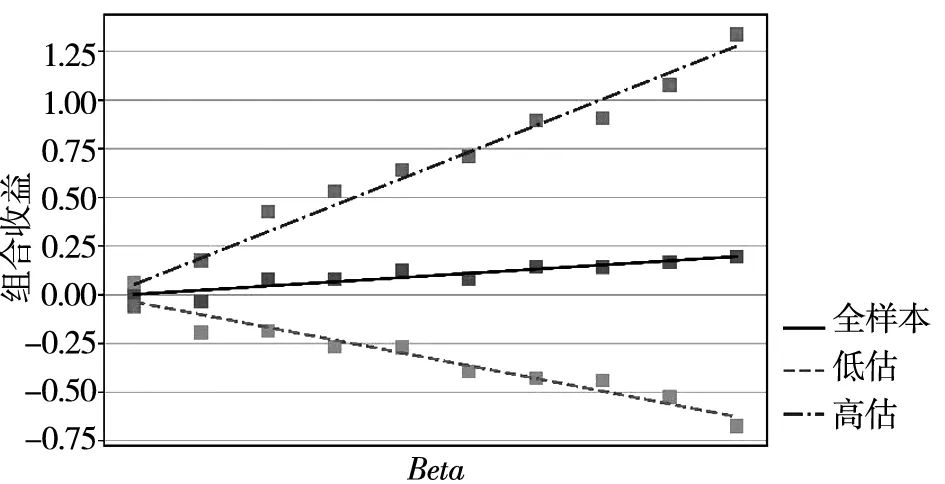
图7 RS指标下的Beta单变量排序结果

表6为Beta的 Fama-MacBeth 回归结果和前面单变量投资组合排序的结果相一致.在低估状态时(RS和IVIX标记)，股票的预期收益率和Beta显著负相关；在高估市场状态(RS标记)，股票的预期收益率和Beta显著正相关.在全样本的状况下，个股预期收益率与Beta的之间关系不显著.在加入控制变量后，高估尾部时期，股票的预期收益率和Beta之间的负向关联仍然显著.表7为DBeta的Fama-MacBeth回归结果.与Beta的结果类似，在高估状态时，股票的预期收益率和DBeta显著正相关；但在低估状态时，DBeta与预期收益率的关系变为负向.在全样本的状况下，个股收益率与DBeta的之间关系不显著.

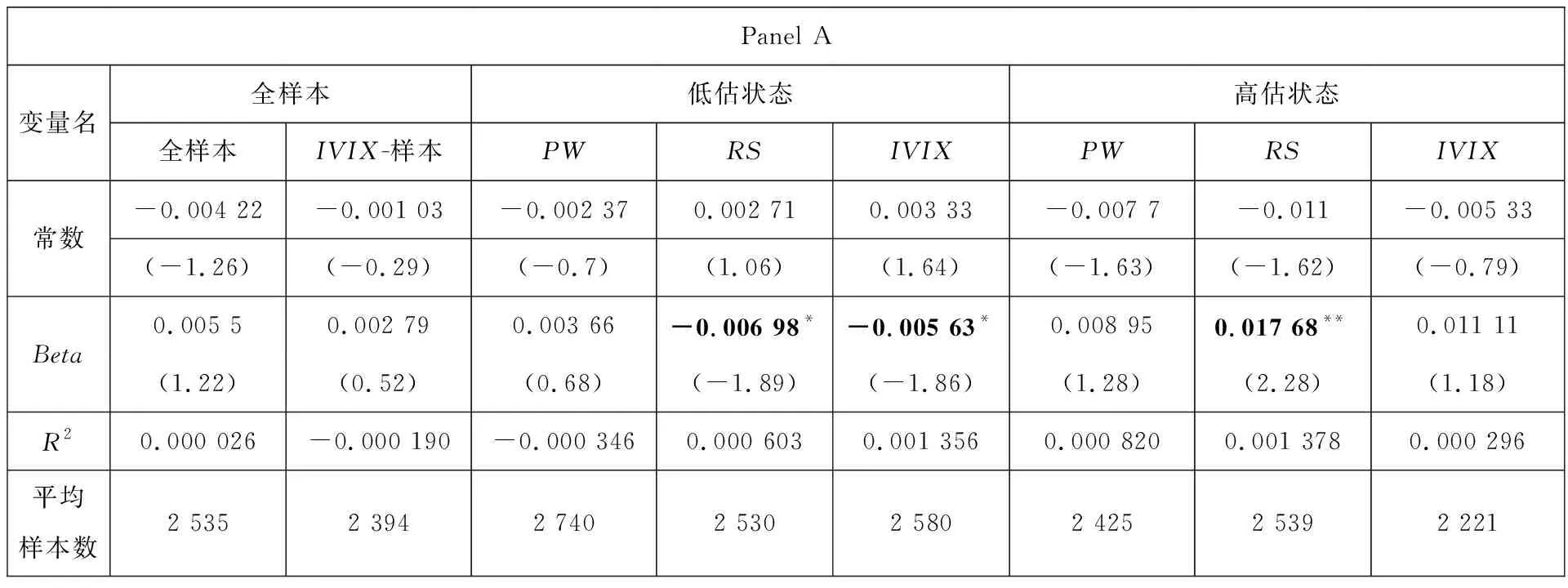
表6 预期收益率与Beta的Fama-MacBeth回归结果

表7 预期收益率与DBeta的Fama-MacBeth回归结果

综上，概率扭曲通过影响投资者对尾部风险的感知，对于系统性风险定价确实会产生影响.当投资者高估尾部风险，个股的Beta(DBeta)和预期收益率呈正向关联，这与传统的CAPM模型预测的结果一致.然而，当投资者低估尾部风险时，个股的Beta(DBeta)和预期收益率是负向相关的.如果不用概率扭曲强弱程度分离出两个时期的风险态度转变，正负相抵，就会得到全样本下的Beta(DBeta)与收益没有显著关系(Beta异象).这也从实证的角度再次证明，概率扭曲为理解A股市场的风险定价提供了可靠的渠道.

续表6

2.3.3 面板回归结果

在前面的Fama-MacBeth回归中，用概率扭曲指标划分样本为高估和低估时期，考察概率扭曲在不同样本时期的定价作用.出于稳健性的考虑，本节使用虚拟变量来进一步考察概率扭曲对于A股市场风险定价的影响.

具体地，采用适合金融数据的固定效应面板回归，并添加虚拟变量以标记高估/低估尾部时期.面板回归如下

Returni,t=a+b1Betai,t+b2Dummyt×

Betai,t+b3Contrli,t

(18)

其中Dummyt取值为1代表市场处于高估尾部状态，取值为0代表低估状态.这样引入虚拟变量可以清晰地刻画概率扭曲的影响，Beta前的系数b1代表了低估状态时风险溢价水平，Beta×Dummy乘积项前系数b2代表了概率扭曲处于高估状态时的增量影响.换句话说，b1+b2代表了高估状态时的风险溢价水平.如果面板回归结果与前面的Fama-MacBeth回归结果一致，那么b1应该显著为负，而b2应显著为正，且b2的数值水平应远大于b1以保证b1+b2符号为正.

表8的Panel A和Panel B为预期收益与Beta关系的面板回归结果.结果与本文的预期完全一致，b1显著为负，b2显著为正.单从统计结果来看，面板回归的结果甚至强于Fama-MacBeth 回归结果：表现为更多的显著性结果，更强的显著性水平.以RS指标为例，面板回归结果显示：市场低估状态下的Beta风险溢价水平为-0.007 37(99%水平显著)；市场高估状态下，Beta风险溢价水平为0.012 95(99%水平显著).Fama-MacBeth回归结果显示(表6)：市场低估状态下的Beta风险溢价水平为-0.006 98，在90%水平下显著；市场高估状态下，Beta风险溢价水平为0.017 68，在95%水平下显著.加入控制变量，面板回归结果不变.表8的Panel C和Panel D为预期收益与DBeta关系的面板回归结果，同样与Fama-MacBeth的结果一致.在低估状态时，DBeta与预期收益率呈负向关系；在高估状态时，DBeta与预期收益率则呈正向关系.

表8 预期收益率与Beta/DBeta 的面板回归结果

综上所述，不管是加入了虚拟变量后的面板回归，还是Fama-MacBeth的分样本回归结果都与前面的理论模型结果相一致.即当投资者高估尾部风险时，个股的Beta(DBeta)和预期收益率关系与传统CAPM模型一致，为正向相关；当投资者低估风险时，Beta(DBeta)和预期收益率呈负向相关.而如果不用概率扭曲区分高估/低估时期，正负相抵，可能得到预期收益率与风险关系不显著的实证结果.

2.4 概率扭曲对于特质风险定价影响

在完成概率扭曲对于系统性风险的定价影响分析之后，本文进一步来检验概率扭曲对特质风险定价的影响.特质波动率(idiosyncratic volatility，IV)是特质风险的一个代理变量.与系统性的市场风险不同，特质风险被认为是上市公司面对的特有风险、是可以被分散化的.既然是可以被分散化的风险，经典的定价理论认为特质风险不存在风险补偿，即特质波动率与收益之间应该没有显著关系.长久以来，大量的实证研究也试图搞清楚特质波动率和股票预期收益率之间是否存在某种关系.早期的理论倾向认为特质波动率和预期收益率之间存在正相关(比如Merton[42]).然而，Ang等[43]指出特质波动率和预期收益率之间负相关 —— 即当其他条件相同时，特质波动率低的股票未来可能获得更高的收益，这便形成了特质波动率之谜(idiosyncratic volatility puzzle).

Liu等[13]实证研究发现，高特质波动率的股票往往也是高Beta的股票.前面的理论和实证研究已经表明概率扭曲对于高Beta股票的价格高估有一定的解释作用.那么，可以预见概率扭曲对于特质波动率的定价也应该起作用.具备高特质波动率的股票往往更容易发生尾部极端回报，如果投资者又恰好处于忽视尾部极端损失风险的低估时期，那么这类高特质波动率股票的价格会进一步高估，因此本文预期收益和IV的负向关联在低估时期应该更加显著.反之，如果投资者能够重视尾部风险(高估时期)，这类高特质波动率股票的负向收益应该削弱(甚至特质波动率呈理性的正向定价).下面的回归结果证实了本文的猜想.

表9是同时考虑系统性风险和特质风险的Fama-MacBeth 回归结果.Panel A选用Beta作为系统性风险指标，Panel B选用DBeta作为系统性风险指标，都以特质波动率IV为特质风险指标.首先，在全样本下，Beta/DBeta和预期收益无显著关系，特质波动率IV和预期收益也无显著关系.在低估状态下，Beta/DBeta和预期收益负相关，IV与预期收益也呈负向关联，IV变量前系数分别为-0.000 09和-0.000 13，在5%的水平上显著.在高估状态下，Beta/DBeta和预期收益正相关，IV与预期收益也呈显著正向关联，IV变量前系数则变为0.000 19和0.000 21，同样在5%的水平上显著.

表9 同时考虑系统性风险和特质风险的Fama-Macbeth回归结果

续表9

表10为面板回归结果.与前文类似，通过引入虚拟变量Dummy来检验概率扭曲对于系统风险与特质风险的影响.IV前的系数代表了低估状态下的特质风险溢价水平，而Dummy×IV的乘积项系数代表了高估状态下的增量影响.面板回归的结果与Fama-MacBeth的结果一致.在低估状态影响下，IV和Beta/DBeta与预期收益率呈现负向的关系.而在高估状态下，IV则和预期收益率显著正向相关.

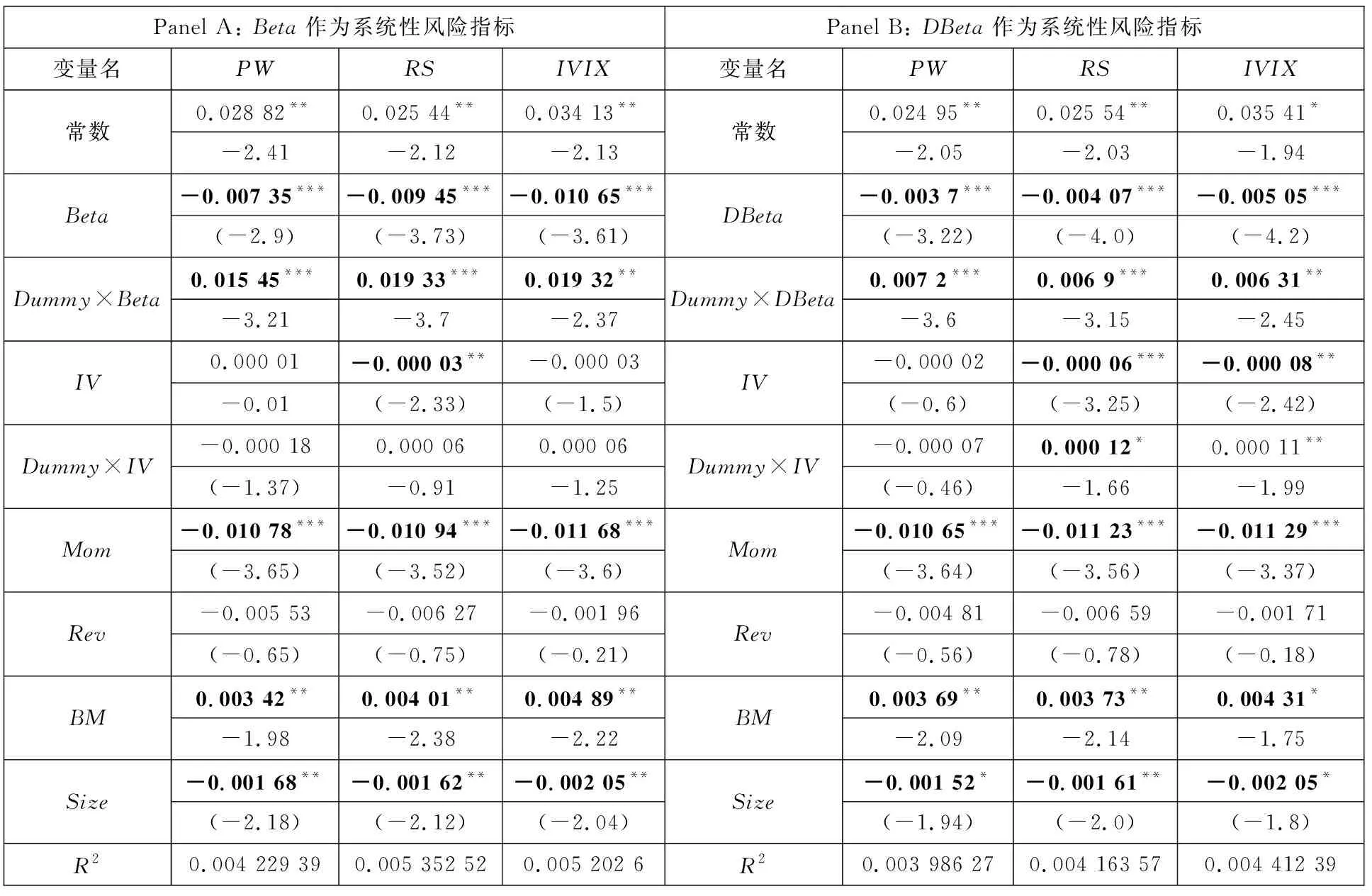
表10 同时考虑系统性风险和特质风险的面板回归结果

综上，概率扭曲通过影响投资者对于尾部风险的感知会同时影响系统性风险和特质风险的定价.当投资者高估尾部风险时，不管是系统性风险还是特质性风险都与预期收益率呈理性的正向相关，这与传统CAPM模型预测一致.然而，当投资者低估尾部风险时，不管是系统性风险还是特质性风险都与预期收益率呈负向关联.而如果不用概率扭曲区分尾部的高估和低估时期，正负相抵，则得到经验检验中A股市场风险与收益关系不显著的实证结果(这正是经典CAPM模型在实证检验中的困难之处，也称为Beta异象).本文的实证结果一再表明，概率扭曲为解释Beta异象提供了一个新的视角，为理解A股市场的风险定价提供了一条可靠的渠道.

3 结束语

本文从理论和实证上讨论了概率扭曲对于A股市场系统性风险和特质风险定价的影响.首先，通过理论推导RDU-CAPM，发现概率扭曲通过影响投资者对于尾部风险的感知强弱程度从而扭曲定价核，进而影响风险与收益的定价关系.具体地，发现低估尾部风险，有时甚至会扭曲投资者原本的风险厌恶态度而呈现出风险喜好行为，进而扭曲风险和收益之间的理论正向定价关系为负向关联.换句话来说，本文认为投资者低估尾部风险是Beta异象中风险被负向定价的一个可能来源.实证上，通过50ETF期权数据，首先发现A股市场投资者低估尾部风险状态(即钟型定价核)占主导，这一结果和美国市场不同.此外，本文还构建了一系列概率扭曲指标来定量衡量市场整体的概率扭曲强弱程度，并通过这些指标将市场分为高估和低估尾部状态，最后使用Fama-MacBeth回归和面板回归检验了概率扭曲对于A股市场的系统性风险和特质风险定价的影响.本文的主要实证结论为：当投资者高估尾部风险时，不管是系统性风险和特质风险都被理性正向定价(这与传统CAPM模型理论一致)；当投资者低估尾部风险时，不管是系统性风险和特质风险都被负向定价；而如果不运用概率扭曲区分高估和低估时期，全样本状态下，正负相抵，不管是系统性风险和特质风险都与收益关系不显著.因此，本文运用概率扭曲强弱程度分开讨论高估/低估尾部风险时期，一方面可以厘清概率扭曲(投资者尾部风险感知强弱程度)对于风险和收益定价关系的影响；另一方面，也为传统CAPM模型在实证检验中的困难提供了一条可能解决之道.

本文的主要贡献在于提供了一个新的视角(概率扭曲)来理解A股市场的风险定价.研究发现，概率扭曲通过影响投资者对于尾部风险的感知会同时影响系统性风险和特质风险的定价.政策意义上，监管部门需要关注市场的概率扭曲程度，做出相应措施，防范系统性风险发生.