基于动态SEIR模型的传染性疾病预测和政策评估①

方匡南， 任 蕊， 朱建平 ， 马双鸽， 王晓峰

(1. 厦门大学经济学院， 厦门 361005； 2. 厦门大学管理学院， 厦门 361005；3. 厦门大学健康医疗大数据国家研究院， 厦门 361005； 4. 耶鲁大学公共卫生学院, 纽黑文 06501， 美国； 5. 美国克利夫兰医院量化健康科学系， 克利夫兰 44195， 美国)

0 引 言

突发传染病指严重影响社会稳定、对人类健康构成重大威胁，需要对其采取紧急处理措施的新发生的急性传染病和不明原因疾病等.近些年来，非典型性肺炎(Severe Acute Respiratory Syndrome，SARS)、中东呼吸症(Middle East Respiratory Syndrome，MERS)等突发传染病对社会稳定以及经济发展造成严重影响、给人类生命健康带来巨大威胁.对突发传染病的发展趋势进行及时监控和预测，向民众提供传染病预警，帮助公共卫生部门及时采取相应措施、阻断传染病进一步扩散，对于维护社会稳定发展、保障民众生命安全具有重要的现实意义.

传染病的预测有着悠久的历史，其中最经典的预测模型是Kermack等利用动力学方法建立的SIR(Susceptible Infectious Removed)模型[1]，该模型最早用于研究伦敦的黑死病，将传染病系统内的个体状态划分为易感态、感染态和移除态.随后，一些学者在SIR模型的基础上提出了许多衍生模型，比如SEIR(Susceptible Exposed Infectious Removed)模型[1， 2]，相比SIR模型，SEIR模型假设个体存在潜伏期状态，认为个体在潜伏期已感染病毒但仍未发病，具有传染性但未被发现和隔离[2-4].SEIR模型被广泛应用在SARS和MERS等疫情研究中[5， 6]，并且有比较好的预测效果，在此类传染病疫情的研判和控制中发挥了重要的作用.

一些学者利用SIR或SEIR模型对COVID-19传染病爆发初期的传播情况进行了分析和预测[5, 7-10].比如Wu等根据2019年12月31日到2020年1月28日的数据，利用SEIR模型估计出武汉市传染病爆发初期病毒的基本再生数和倍增时间[5]；Read等根据2020年1月22日前的数据，在不考虑防控干预措施的情况下，利用SEIR模型预测出武汉市在2020年1月29日的传染病患病个数将高达10.5万人，将远超出实际的确诊人数[8].此外，一些学者对经典的传染病动力学模型进行改进并对此次传染病传播的后续发展进行预测[6, 11-16].比如黄森忠等利用修正的SEIR模型估计了感染人数、拐点时间、病毒基本再生数等，但该模型假设模型中传染率和移除率等参数固定不变[6]；曹盛力等结合追踪隔离的干预措施，提出潜伏态和感染态患者均具备传播能力的SEIR模型[11]；Shao等通过建立考虑人口跨区域流动的SEIRD模型，基于模拟实验对三种控制传染病传播的措施(隔离感染者、减少人口流动、改善治疗条件)效果做出了评估[12]；Yang等认为人口迁移对病毒传播有很大影响，提出带人口迁移的修正SEIR模型，对中国湖北、广东等省份的传染病疫情发展进行了预测分析[13]；Wang等、张原等通过新型随机动力学模型对此次突发传染病在海外的发展趋势进行了估计和预测[15， 16].

首次流行的突发重大传染病初期的诊断和治疗力量不足，容易在短时间内造成公共医疗资源的需求骤增和严重短缺，进而导致传染病传播初期的高病死率.除此以外，传统SEIR模型没有考虑防控干预措施和人口流动对传染病传播的影响，基于以上因素，本文提出动态SEIR模型，基于实际数据动态地估计传染病系统的重要参数，更准确地预测传染病的传播趋势，体现出突发重大传染病的新发性和相应防控措施的有效性和充分性.

1 SEIR模型

SEIR模型假设传染病系统内的每个个体都处于以下4种状态之一[23]：

1)易感态S (susceptible)，指个体处于传染病流行范围内但未被感染，属于高危人群；

2)潜伏态E (exposed)，指个体已被感染但仍未发病，处于潜伏期；

3)感染态I(infected)，指个体已经发病且具有传染性，病毒可以传播给S类成员，将其变为E类或I类成员；

4)移除态R(removed)，指个体死亡或因病愈而具有免疫力，不会面临再次感染的危险.

SEIR模型可用方程组(1)表示，演化过程如图(1)所示.其中S(t)，E(t)，I(t)，R(t)分别表示t时刻易感态、潜伏态、感染态和移除态的个体数，传染率β表示一个感染态个体与易感态个体接触，导致易感态个体被感染进入潜伏期的概率；发病率κ是一个潜伏态个体在单位时间内转变为感染态的概率，1/κ表示潜伏期时长；移除率γ是一个感染态个体在单位时间内转变为移除态的概率.

图1 SEIR传染病模型

SEIR模型假设传染率β，发病率κ和移除率γ均为固定不变的常数，且系统内人口总数N保持不变，即N(t)=S(t)+E(t)+I(t)+R(t)

{dS(t)dt=-βS(t)I(t)N

dE(t)dt=βS(t)I(t)N-κE(t)

dI(t)dt=κE(t)-γI(t)

dR(t)dt=γI(t)

(1)

2 动态SEIR模型

2.1 模型设定

假设每个个体都处于易感态、潜伏态、感染态和移除态4种状态之一，见图2.与SEIR模型不同，动态SEIR模型假设：

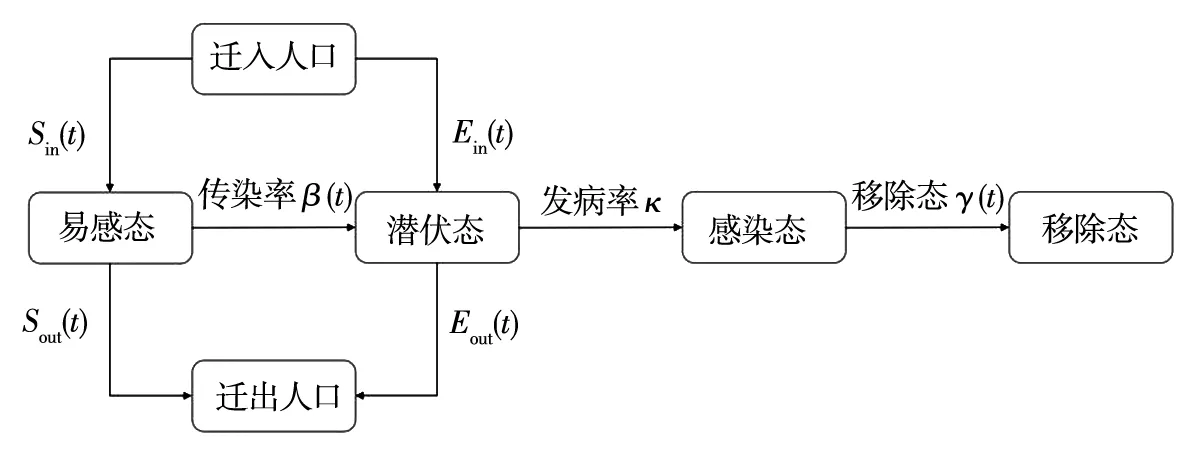
图2 人口规模可变的SEIR传染病模型

1)传染率β(t)和移除率γ(t)是随时间变化的函数；

2)人口迁移会导致系统内人口总数发生变化.用Sin(t)和Sout(t)表示t时刻迁入及迁出该地区的易感态个体数，Ein(t)和Eout(t)表示t时刻迁入及迁出该地区潜伏态个体数，因此人口总数N(t)满足关系

N(t+1)=N(t)+Sin(t)-Sout(t)+

Ein(t)-Eout(t)

动态SEIR模型可描述为方程组(2)

{dS(t)dt=-β(t)S(t)I(t)N(t)+Sin(t)-Sout(t)

dE(t)dt=β(t)S(t)I(t)N(t)-κE(t)+Ein(t)-Eout(t)

dI(t)dt=κE(t)-γ(t)I(t)

dR(t)dt=γ(t)I(t)

(2)

用s=S(t)/N(t),e=E(t)/N(t),i=I(t)/N(t),r=R(t)/N(t)表示各状态个体数占当前总人口数的比例；sin=Sin(t)/N(t)，sout=Sout(t)/N(t)，ein=Ein(t)/N(t)，eout=Eout(t)/N(t)表示各状态下迁入、迁出该地区的人口数占当前总人口数的比例，则模型(2)可转化为模型(3)，详细证明过程见附录，其中s(t)+e(t)+i(t)+r(t)=1，Δ=sin(t)-sout(t)+ein(t)-eout(t).

{s(t+1)=s(t)-β(t)s(t)i(t)+sin(t)-sout(t)1+Δ

e(t+1)=e(t)+β(t)s(t)i(t)-κe(t)+ein(t)-eout(t)1+Δ

i(t+1)=i(t)+κe(t)-γ(t)i(t)1+Δ

r(t+1)=r(t)+γ(t)i(t)1+Δ

(3)

借鉴Wang等[24]eSIR模型的建立方法，定义θSt、θEt、θIt、θRt分别是个体t时刻处于易感态、潜伏态、感染态、移除态的概率(下文统称θ*t为各状态下的流行率).假设δin(t)为t时刻单位人口的迁入率，等于易感态个体迁入概率和潜伏态个体迁入概率的总和，δin(t)=δSin(t)+δEin(t).δout(t)表示t时刻单位人口的迁出率，等于易感态个体迁出概率和潜伏态个体迁出概率的总和，即δout(t)=δSout(t)+δEout(t).利用图3所示的动态SEIR状态空间模型，对二维时间序列(YIt,YRt)进行预测，其中YIt表示t时刻该地区现存感染病例占总人口数的比例，YRt为累计移除病例占总人口的比例.假设观测的数据(YIt,YRt)由四维隐马尔可夫过程θt=(θSt,θEt,θIt,θRt)T推导所得，本文联立θt=(θSt,θEt,θIt,θRt)T和(YIt,YRt)之间的方程，借助马尔可夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法[25]得到其潜在关系.

图3 动态SEIR状态空间传染病模型

假设序列(YIt,YRt)在t时刻遵循如下状态空间模型

{YIt|θt,τ～Beta(λIθIt,λI(1-θIt))

YRt|θt,τ～Beta(λRθRt,λR(1-θRt))

θt|θt-1,τ～Dirichlet(kf(θt-1,β,γ,κ))

(4)

在此假设下，预期的现存感染比例YIt和累计移除比例YRt等于相应状态t时刻的流行率，即E(YIt|θt)=θIt，E(YRt|θt)=θRt.其中λI，λR，k是控制对应分布方差的参数，f(θt-1,β,γ,κ)用来确定狄利克雷分布的均值，由t-1时刻的流行率θt-1=(θSt-1,θEt-1,θIt-1,θRt-1)T控制，θt状态间的转移可用式(5)表示，该方程组没有解析解，所以在实际计算中用四阶龙格-库塔(Runge-Kutta)方法计算其近似值

{θSt+1=θSt-β(t)θStθIt+δSin(t)-δSout(t)1+Δδ

θEt+1=θEt+β(t)θStθIt-κθEt+δEin(t)-δEout(t)1+Δδ

θIt+1=θIt+κθEt-γ(t)θIt1+Δδ

θRt+1=θRt+γ(t)θIt1+Δδ

(5)

其中Δδ=δSin(t)-δSout(t)+δEin(t)-δEout(t)，且对任意时间t，θSt+θEt+θIt+θRt=1.

随着防控干预措施的加强以及公共防护意识的提高，传染率应逐渐降低.借鉴Wang等[24]的想法，引入修正因子π1(t)∈[0,1]来修正易感者与感染者相遇的机会，从而构造出随时间变化的传染率β(t)=β0π1(t).如果该地区没有实施任何干预措施，修正因子π1(t)≡1，见图4(a).若采取了有效的干预政策，π1(t)可以根据具体的干预政策进行调整，比如用阶梯函数、指数函数(π1(t)=e-bt)等随时间推移而传染率逐渐减小的函数形式来修正β(t)，见图4(b)和图4(c).

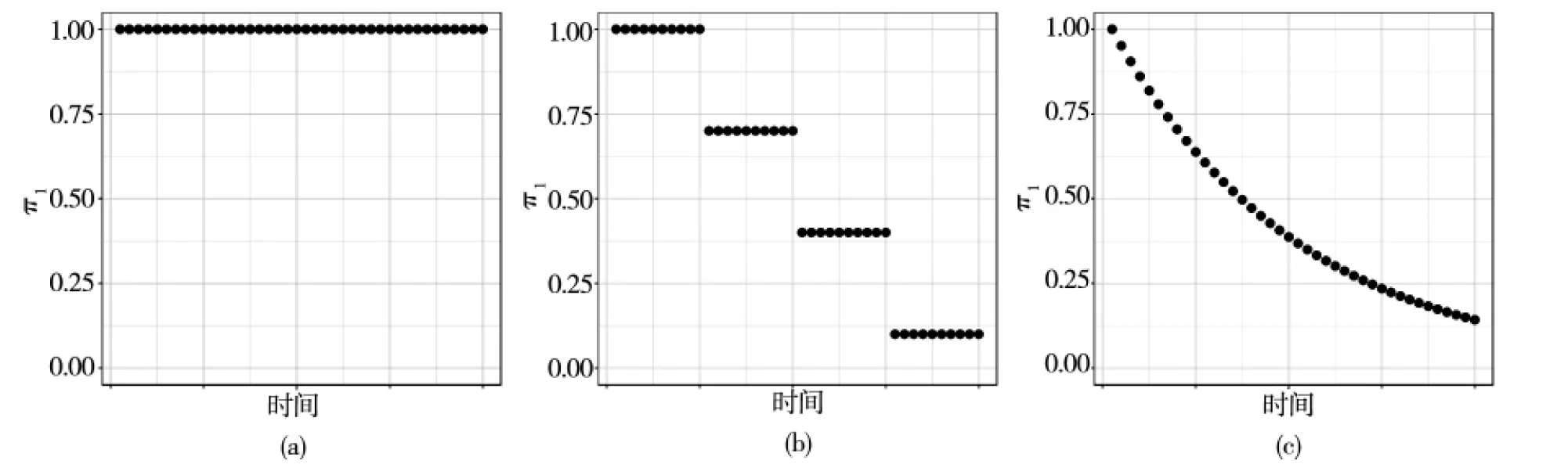
图4 修正因子π1(t)

传染病爆发初期，对疾病了解有限且医疗资源紧张，随着对疾病的深入了解、临时医院的建立，医疗资源逐渐充足，移除率也应随医疗条件好转而逐渐增高.同样地，引入π2(t)∈[0,1]来修正感染者治愈成为移除者的机会，即构造时变移除率γ(t)=γ0π2(t).如果不考虑移除率的变化，修正因子π2(t)≡1, 见图5(a).如果将医疗条件的变化纳入考虑，根据该地区的医护资源容量和医疗水平变化对π2(t)进行修正，可以用阶梯函数，指数函数(π2(t)=ebt)等随时间推移而移除率逐渐增加的函数形式来修正γ(t)，见图5(b)和图5(c).

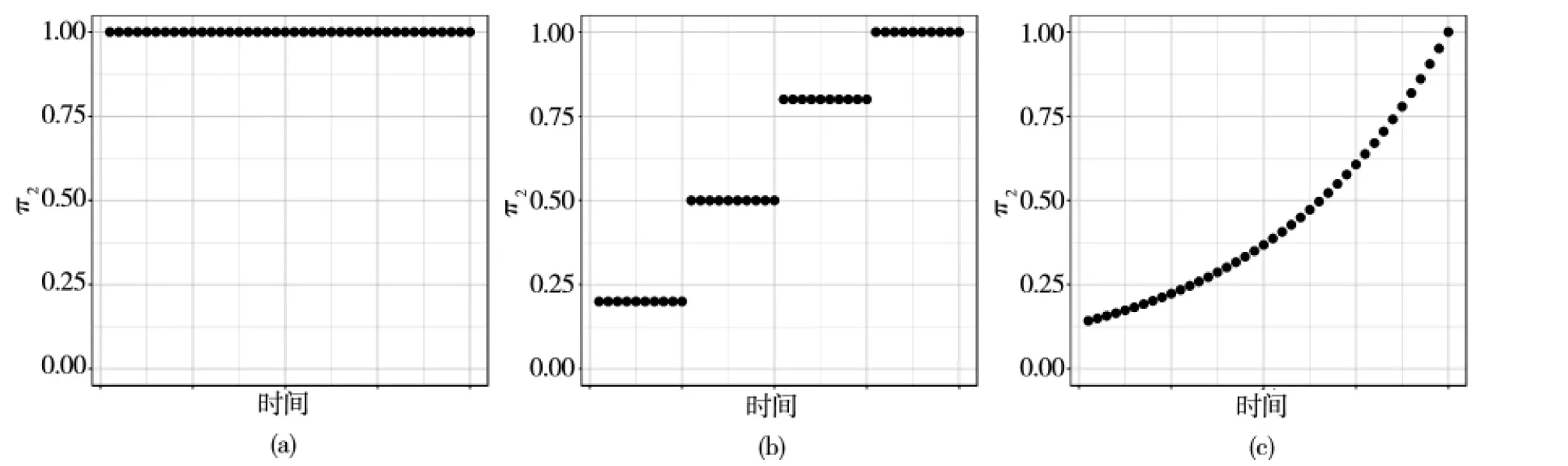
图5 修正因子π2(t)

2.2 模型求解

为求解模型参数τ=(β0,γ0,κ,θ0,λI,λR,k)，在已知数据(YI1:T0,YR1:T0)的情况下，用马尔可夫链蒙特卡洛方法得到参数τ的值及其后验分布.首先，根据Zhao等[10]对基本再生数(2.24～3.58)的研究结果，以及Yang等[13]关于潜伏天数、传染率、移除率的设定，借鉴Wang等[24]eSIR模型的设置，对τ的先验分布做如下设定:

θI0～Beta(1,(YI1)-1),λI～Gamma(2,0.000 1);

θE0～Beta(1,(YI1:7)-1),λR～Gamma(2,0.000 1);

θR0～Beta(1,(YR1)-1),k～Gamma(2,0.000 1);

R0～LnN(1.046,0.105),E(κ)=1/7,SD(κ)=0.1;

γ0～LnN(-2.833,1.775),E(γ0)=1/7,SD(γ0)=0.1;

κ～LnN(-2.833,1.775),E(R0)=1/7,SD(R0)=0.1;

θS0=1-θI0-θR0-θE0,β0=R0γ.

基于上述先验信息，用马尔可夫链蒙特卡洛方法随机采样M=2e6次的结果中位数来估计参数τ，用每次结果的后验分布[θt|θ(m)t-1,τ(m)]对之后p天的流行率进行预测，m=1,…,M

θ(m)t～[θt|θ(m)t-1,τ(m)]

(6)

假设t∈[T0+1,T0+p]的现存感染比例YIt及累计移除比例YRt等于相应状态流行率的预测值，即

{YIt^≈E(YIt|θt)=θIt

YRt^≈E(YRt|θt)=θRt

随后，用M次预测结果的中位数作为流行率的最终预测值.

3 传染病传播趋势的分析与预测

3.1 数据来源

选取2020年在湖北省爆发的突发传染病和相应防控措施作为研究对象，研究传染病传播的规律及模型重要参数等.

病例数据均取自百度网站[17]公布的官方统计数据，包括现存感染病例及累计移除病例数，根据国家统计局公布的2018年的人口统计数据计算出研究地区现存感染比例YIt及累计移除比例YRt.此外，结合百度迁徙提供的迁徙规模指数[18]及往年春运的人口流动情况，对每日迁入地区及迁出地区的人口数进行估计，而迁入、迁出人口数与当前总人口的比值分别是t时刻单位人口迁入率、迁出率的近似值.

3.2 传染病传播趋势的分析与预测

假定2020年1月10日湖北省总人口数为常住人口5 917万，根据2020年1月10日～2020年3月31日的病例数据并结合湖北省各地于2020年1月23日后陆续封闭出入通道(“封城”)的措施，假设2020年1月23日前人口流动情况为δout(t)=δSout(t)+δEout(t)，δSin(t)=δin(t).2020年1月23日后不再存在人口流动.借鉴Yang等[13]对迁入、迁出人口流向的处理方法，定义

δEout(t)δSout(t)=PE(t)1-PE(t)

(7)

PE(t)=e×t时刻新增感染人数t时刻地区总人口数

(8)

其中PE(t)表示单位流出人口处于潜伏态的概率，e表示该地区新感染人数与现存感染人数的关联系数.此外，假设传染率β(t)是分段常值函数，实施关键的干预措施时，传染率会有跳跃性地降低.根据湖北省防控政策的几个重要时间节点指定传染率β(t)如下

β(t)={β0π11, 1月23日前(武汉“封城”)

β0π12, 1月24日～2月05日

(火神山医院、雷神山医院开放)

β0π13, 2月06日～2月12日

(方舱医院投入使用)

β0π14, 2月13日后

同样的，根据湖北省医疗条件变化的几个重要时间节点指定移除率γ(t)如下

γ(t)={γ0π21, 2月05日前

(火神山医院、雷神山医院开放)

γ0π22, 2月06日～2月12日

(方舱医院投入使用)

γ0π23, 2月13日～2月22日

(多家医院“床等人”，医护资源充足)

γ0π24, 2月23日后

按上述时间节点设置修正因子，并将其作为未知参数加入模型进行估计，假设其先验分布均为[0,1]上的均匀分布.

π1(t)=(π11,π12,π13,π14)

π2(t)=(π21,π22,π23,π24)

根据2020年1月10日～2020年3月31日的数据，结合动态SEIR模型对湖北省2020年3月31日前的传染病发病情况进行分析，并对之后的传播趋势进行预测，结果见图6，其中实心点表示用来训练模型的实际数据，实线表示模型的预测值，阴影部分表示预测值的95%置信区间.在继续实施严格的防控干预措施、医护资源充足且不考虑境外输入的情况下，预测此次突发传染病有望在2020年4月中下旬得到控制，与Yang等[13]得到的预测结果相似.

图6 湖北省传染病感染人数预测结果

为评估模型的预测效果，用2020年1月10日至2020年3月3日的数据对模型进行训练，并对2020年3月4日～2020年3月31日的现存感染人数进行为期28天的预测，预测情况见图7(a)，其中空心点表示未参与模型训练的实际数据.将本文提出的动态SEIR模型(dSEIR)与SIR状态空间传染病模型[24](eSIR)，未修正的SEIR模型(SEIR，参数借鉴Geng等的设置[26])和考虑人口跨区域流动的修正SEIR模型[13](mSEIR)进行预测效果的比较，见图7(b).可以看出：动态SEIR模型的预测结果与真实值最接近，说明该模型对湖北省此次传染病传播趋势有比较可信的预测效果.此外，2020年3月4日后现存感染病例的人数下降很快，说明在政府防控下此次传染病传播已进入可控范围内.

图7 动态SEIR模型的预测效果以及和其他模型预测结果的对比

4 防控措施评估

4.1 传染病模型关键参数的估计和评估

对传染病传播规律进行回溯研究并评估相应的防控措施非常重要，首先基于动态SEIR模型对传染病模型的关键参数进行估计和分析，关键参数包括基本再生数R0，有效再生数Rt，发病率κ,传染率β(t)=β0π1(t)和移除率γ(t)=γ0π2(t).基本再生数R0指一个感染态个体在移除感染系统前平均能感染的人数，在真实的病毒传播过程中，由于实施政府干预政策、增强人为防护措施等外在因素影响，感染系统将不再满足基本再生数的定义条件，所以大多情况下采用有效再生数Rt衡量病毒传播情况，即传播过程中一个感染态个体在t时刻可感染的平均人数，Rt<1时认为传染病流行趋势已被控制，即将走向消亡.本文根据已知数据训练模型参数(β0,γ0,κ)，用R0=β0/γ0估计基本再生数R0，Rt=β(t)/γ(t)估计有效再生数Rt.

2020年1月23日武汉“封城”后，传染病传播进入了有防控干预的传播状态，2020年2月2日后，湖北省多地呼吁公众居家隔离，不外出不聚集，并切实限制社区居民外出，加强对确诊病例的隔离，因此认为病毒在2020年2月2日后进入有防控政策的强干预传播状态.假设湖北省2020年1月23日及以前出现症状的感染者是无防控干预下传染病自由传播期间感染的，2020年1月23日后出现症状的感染者是在防控干预下的传播期间感染的，用不同时间段的数据对模型进行训练，估计的基本再生数、有效再生数、传染率、移除率和发病率见表1.

表1 基于动态SEIR模型估计出的关键参数

病毒自由传播期间，推算的基本再生数和有效再生数是R0=Rt≈2.914 3，表示一个感染态个体平均能感染3个人，与Zhao等[10]估计的数值范围2.24～3.58基本一致，而在实施防控干预措施后，2020年3月31日有效再生数Rt≈0.313 1，说明病毒传播的速度和范围在很大程度上得到了遏制，传染病的传播趋势已得到控制.1/κ指病毒的潜伏期天数，模型计算的平均潜伏期在6天～8天左右，与Yang等[13]估计的范围基本一致.此外，模型估计的传染率β(t)和移除率γ(t)见图8，其中实点表示模型的估计值，阴影部分表示估计值的95%置信区间.

图8 随时间变化的传染率和移除率

4.2 隔离政策的评估

防控干预措施的本质是控制人员流动，避免病毒在人与人之间过度扩散，减少易感者与感染者之间的接触机会，即减少人口流动δin(t)和δout(t)，降低传染率β(t).根据实际数据，利用动态SEIR模型训练出相关参数(β0,γ0,κ,θ0)，采用马尔可夫链蒙特卡洛模拟的方法对改变“封城”时间的传染病传播情况进行数值仿真.

分别对“封城”政策在2020年1月23日实施，2020年1月18日(提前5天)实施及2020年1月28日(延迟5天)实施进行仿真试验.假设“封城”后湖北省不再存在人口流动，δin(t)=δout(t)=0，如果政策延迟5天，用2019年同期的迁徙规模指数对迁入率、迁出率进行估计[18]，并假设之后的迁入率、迁出率为零.模拟实验(20万次)的结果均值见表2.

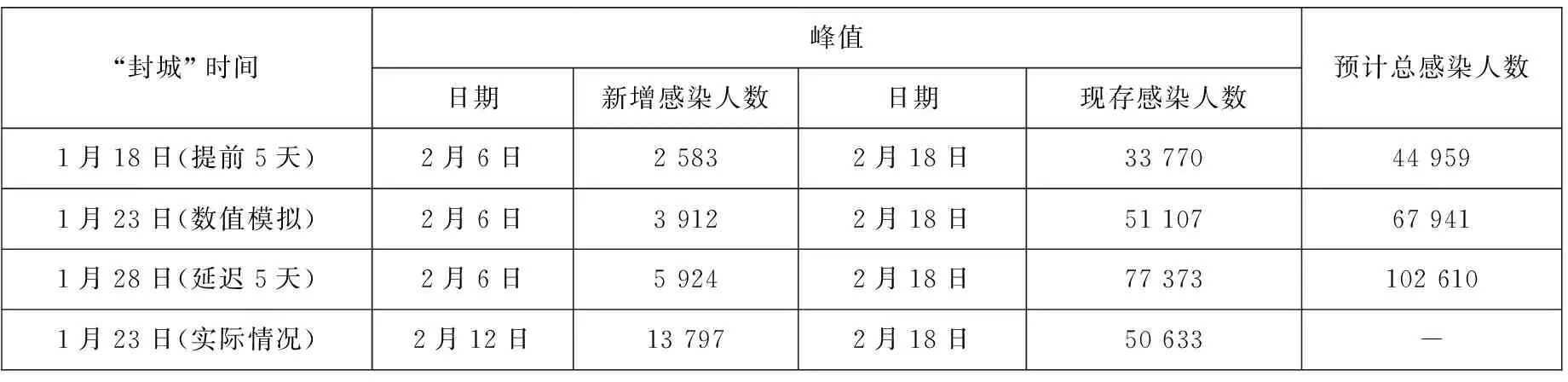
表2 “封城”政策对传染病传播影响的评估

根据上文对此次突发传染病的分析，预测传染病传播趋势将在4月中下旬得到控制，且累计感染人数约达67 941例.值得注意的是，2020年2月12日起湖北省将临床诊断病例计入新增病例中，这种统计口径的变化导致当天新增感染病例共计13 797例，这是数值模拟中当日新增感染人数峰值结果与实际情况产生分歧的主要原因.模拟研究发现：如果在2020年1月23日进行“封城”，预计在2020年2月18日达到现存感染人数的高峰，约51 107例，总感染人数达到67 941例；如果提前5天采取政府倡导的防控隔离措施，预计2020年2月18日达到33 770例的高峰，总病例数约44 959例；但如果延迟5天实施，现存感染人数将在2020年2月18日达到77 373例的高峰，比实际感染人数峰值高出26 266例，且预计总病例数将达到102 610人，远高于实际感染病例总数，这说明“封城”措施能很好地遏制传染病大幅扩散.

4.3 集中收治政策的评估

2020年2月，武汉市分别开建火神山医院、雷神山医院及多家方舱医院，并逐步投入使用，集中收治患病病例，随后，湖北省实行“四类人员”分类集中防控，对所有确诊患者集中救治，疑似患者集中收治，发热患者集中留观治疗，密切接触者隔离观察.集中收治措施在本质上为感染者提供更好的治疗条件，提高感染者治愈成为移除者的可能，同时对其实施严格的隔离措施，阻断了住院的感染者与易感者直接接触的机会.

基于动态SEIR模型，采用马尔可夫链蒙特卡洛模拟的方法对改变医院开放时间的疫情情况进行数值仿真，分别对集中收治措施提前3天实施及推迟3天实施的情况进行20万次模拟，结果见表3.可以看出，如果湖北省提前3天采取集中收治措施，能够及时遏制感染人数增长的趋势，预计总感染人数为37 770.如果延迟3天采取集中收治措施，由于自我隔离措施的不到位以及医疗条件的紧缺，新增感染人数和现存感染人数都会更快、更早地到达峰值，且预计感染人数峰值将达到92 134人，总感染人数高达122 297人，远高于实际总感染人数.因此，集中收治措施使患者更快、更好地得到治疗，同时阻断了传染病进一步地传播、扩散，充分做到了时间上的及时性和方向上的正确性.

表3 集中收治政策对传染病传播影响的评估

5 结束语

本文提出的动态SEIR模型可以根据传染病的传播特点和防控干预措施对模型参数进行动态估计，并提供了相应的R软件包dSEIR供研究者使用(https://github.com/ruiqwy).相对于传统SEIR模型假设封闭环境，动态SEIR模型将人口流动对疾病传播的影响纳入考虑，更符合突发重大传染病的传播特点，使模型具有更好的预测效果.

基于动态SEIR模型，对湖北省2020年重大突发传染病的流行趋势和相关防控措施进行研究评估，为后续的突发传染病防控贡献了有效的“湖北经验”：1)“封城”的隔离措施非常重要，政府的果断决策对传染病传播扩散产生了很好的遏制效果.2)“四类人员”分类集中防控的措施，火神山医院、雷神山医院及方舱医院的陆续建立，对于及时救治传染病病例、尽早控制发病趋势起到了非常重要的作用.

以此次突发传染病的分析、预测和评估为例，提出如下建议：1)针对重大突发传染病，其他国家和地区可以借鉴此次湖北省防控的成功经验，坚决、迅速的封闭隔离阻断措施能有效控制传染病传播，采取集中收治措施对救治感染患者、控制传染病传播也起到了非常重要的作用；2)传染病防控的重点在于需要依据传染病发展趋势的变化不断调整防控政策，建立动态传播动力学模型及时预警、实时监控、动态科学预测传染病的发展趋势十分重要；3)借助大数据等新兴技术对来自传染病风险区域的人员提前进行预排查，及时对相关人员进行检测和隔离，将传染病传播限制在可控范围内；4)病毒传播不分国界，突发重大传染病会对各国的医疗卫生状况和经济环境造成冲击，传染病防控不应各自为战，需要加强地区合作、联防联控同心携手抵御突发传染病的挑战.

Prediction and policy assessment of infectious diseases transmission using dynamic SEIR model

FANGKuang-nan1,RENRui1,ZHUJian-ping2, 3,MAShuang-ge4,WANGXiao-feng5

1. School of Economics, Xiamen University, Xiamen 361005, China;2. School of Management, Xiamen University, Xiamen 361005, China;3. National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen 361005, China;4. School of Public Health, Yale University, New Haven 06501, USA;5. Department of Quantitative Health Science, Cleveland Clinic, Cleveland 44195, USA

Abstract: The prevention of sudden infectious diseases is a focus issue that has attracted extensive attention in recent years. The sudden infectious diseases not only pose a huge threat to people’s lives and health, but also bring a serious impact on economic development and social stability. It is of great practical significance to achieve timely early warning, real-time monitoring and reasonable prediction of sudden infectious diseases for the prevention and control of infectious diseases. In this study, a dynamic SEIR model based on the Susceptible Exposed Infectious Removed (SEIR) model is proposed to study the spread trend of infectious diseases. The model can not only consider the impact of population movement on diseases transmission, but also dynamically estimate model parameters based on control interventions, which is more consistent with the epidemic characteristics of infectious diseases and has better predictive performance. Finally, the corresponding R software package dSEIR is provided for researchers to use.

Keywords: sudden infectious diseases; dynamic SEIR; prediction of the trend of infectious diseases; policy assessment

附录：

根据本文2.1节对动态SEIR模型的描述，其转移过程可以用如下微分方程组描述

{dS(t)dt=-β(t)S(t)I(t)N(t)+Sin(t)-Sout(t)

dE(t)dt=β(t)S(t)I(t)N(t)-κE(t)+Ein(t)-Eout(t)

dI(t)dt=κE(t)-γ(t)I(t)

dR(t)dt=γ(t)I(t)

假设系统内人口总数随人口流动而发生变动，满足

N(t+1)=N(t)+Sin(t)-Sout(t)+Ein(t)-Eout(t)

人口流动导致N(t)发生变化，使得SEIR模型的动力学行为变得更为复杂.首先对相关符号进行定义，见附表1.

附表1 符号说明

以易感态个体的转移情况为例，根据微分方程组(3)可得

S(t+1)-S(t)=-β(t)S(t)I(t)N(t)+Sin(t)-Sout(t)

(A1)

在公式(A1)左右两侧同时除以t时刻该地区总人口数N(t)，得到公式为

S(t+1)N(t)-S(t)N(t)=-β(t)S(t)I(t)N(t)N(t)+Sin(t)N(t)-Sout(t)N(t)

(A2)

为得到易感态比例的状态转移公式，在公式(A2)第一项的分子分母上同时引入t+1 时刻该地区的总人口数N(t+1)

S(t+1)N(t+1)·N(t+1)N(t)-S(t)N(t)=-β(t)S(t)I(t)N(t)N(t)+Sin(t)N(t)-Sout(t)N(t)

(A3)

根据附表1的符号定义将公式(A3)简化为

s(t+1)N(t+1)N(t)-s(t)=-β(t)s(t)i(t)+sin(t)-sout(t)

(A4)

从而得到易感态比例s(t)的状态转移公式为

s(t+1)=[s(t)-β(t)s(t)i(t)+sin(t)-sout(t)]N(t)N(t+1)

(A5)

定义Δ=sin(t)-sout(t)+ein(t)-eout(t),则N(t)/N(t+1)可改写为

N(t+1)N(t)=N(t)N(t)+Sin(t)-Sout(t)+Ein(t)-Eout(t)=11+sin(t)-sout(t)+ein(t)-eout(t)=11+Δ

(A6)

结合公式(A5)和公式(A6)，推导出如下易感态比例转移公式

s(t+1)=s(t)-β(t)s(t)i(t)+sin(t)-sout(t)1+Δ

(A7)

同理可推得潜伏态比例，感染态比例，移除态比例的转移公式，因此动态SEIR模型的微分方程组可写成如下的形式

{s(t+1)=s(t)-β(t)s(t)i(t)+sin(t)-sout(t)1+Δ
e(t+1)=e(t)+β(t)s(t)i(t)-κe(t)+ein(t)-eout(t)1+Δ
i(t+1)=i(t)+κe(t)-γ(t)i(t)1+Δ
r(t+1)=r(t)+γ(t)i(t)1+Δ

(A8)

各状态下的比例满足s(t)+e(t)+i(t)+r(t)=1.