倒向重随机系统的非零和微分对策问题

许 洁，蔺瑞强

微分对策问题的研究始于20世纪40年代，最初起源于军事需求，美国数学家Issacs 博士及其团队把现代控制理论中的一些概念、原理与方法引入对策论中，Issacs 整理出版的《微分对策》一书，是世界上第一部微分对策专著，标志着微分对策理论的诞生.随着人们对微分对策问题研究的深入，其应用不再局限于军事问题，更被广泛应用在航空、工业控制、经济管理等方面.众所周知，生活中几乎到处都充满了不确定因素，因此选择刻画系统的状态方程时选择随机方程更符合客观实际.随机微分方程的发展更进一步推动了随机微分对策问题的研究.杨依芸等［1］讨论了在部分信息下带跳线性二次平均场类型的二人零和微分对策问题，得到其相应最优控制的反馈表示.张保凯［2］研究了一类带泊松跳的零和线性二次随机微分对策问题，且其扩散项系数不为零，得到了在这种动态的博弈中取得一个均衡点，即最优反馈控制策略对.史敬涛［3］研究了带Poisson 跳跃的零和正倒向随机微分对策的最大值原理与动态规划之间的关系；在一定的可微性假设下，建立了对偶过程、广义Hamilton 函数和值函数之间的联系.王光臣［4］结合正倒向随机微分方程理论和滤波技术，讨论了一类部分可观测信息下线性二次非零和随机微分对策问题.吴霜［5］研究倒向随机时滞系统的微分对策问题，并得到了纳什均衡点满足的必要条件和充分条件，并将其应用到一类最优消费选择问题中.肖华［6］通过研究完全信息和部分信息下的正倒向随机微分方程的随机滤波、最优控制和微分对策，得到了非零和对策均衡点与零和对策鞍点的最大值原理和验证定理.吴臻等［7］对一类以布朗运动和泊松过程为噪声源的正倒向随机微分方程，在单调性假设下，给出了解的存在性和唯一性的结果，并将所得结果应用于带随机跳跃的线性二次非零和微分对策问题之中，得到了开环Nash 均衡点的显式形式.唐矛宁等［8］研究了由Brown 运动和Poisson 随机鞅测度共同驱动的完全耦合的正倒向随机系统的开环双人非零和随机微分对策问题，证明了开环Nash 均衡点存在的一个必要条件及一个充分条件.左姗姗［9］研究了平均场正倒向随机系统的微分对策问题，讨论了零和以及非零和微分对策的最大值原理.

目前，对非零和差分对策的研究越来越广泛，在此类问题研究的基础上，该文探索倒向重随机系统驱动的非零和微分对策问题，利用凸变分技术和对偶方法给出纳什均衡点存在的必要条件.

1 预备知识

1.1 符号说明

首先给出本文中的一些符号.Rn表示n维欧氏空间，Rn×d表示n×d矩阵空间，<·>表示内积，|·|表示Eudidean 范数，AT表示转置矩阵.文中所给符号和不等式都是在dt× dP意义下在[0,T] × Ω 中几乎必然成立.

设(Ω,ℱ,P)是一个概率空间，[0,T]是任意大的时间区间，{B(t):0≤t≤T}是两个取值在Rd、Rl的独立标准布朗运动.设表示ℱ 中所有的P-零集，对于任意的t∈[0,T],则有ℱt=ℱtω∨ℱBt,T.其中：ℱtω=∨σ{W(r)-W(0):0≤r≤t}，ℱBt,T=∨σ{B(r)-B(t)：t≤r≤T}.对任意的t∈[0,T]，显然集合{ℱt} 既不递增也不递减，故不构成信息流.

假设M2(0,T;Rn)={φ(t)|φ(t)为n维ℱt-可测量随机过程且

设ϕ(t) ∈M2(0,T;Rn)定义正向伊藤积分和倒向伊藤积分，这两类积分都是Itô-Skorohod积分.L2(Ω,ℱT,P; Rn)={ξ:ξ是n维ℱt-可测的随机变量并满足E|ξ|2<∞}.

1.2 问题描述

首先考虑受控的倒向重随机系统，其状态方程为：

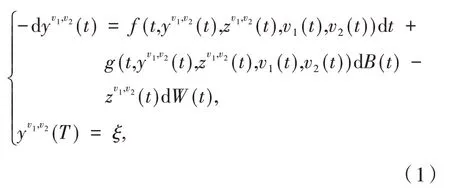
其中：v1(·)和v2(·)分别表示博弈双方的控制过程，设为控制者1 和控制者2.设Ui为Rk的一个非空凸子集.Ui(i=1,2)为满足以下条件的控制过程集合：

①Ui是ℱt-适应的并且vi(t) ∈Ui，t∈[0,T].

Ui中任意元素都被称为控制者的开环容许控制，并被称为他们的容许控制集.除了在结束时间T获得期望的结果ξ外，控制者还同时关心自己的利益.可以使用以下价值泛函来表示，即

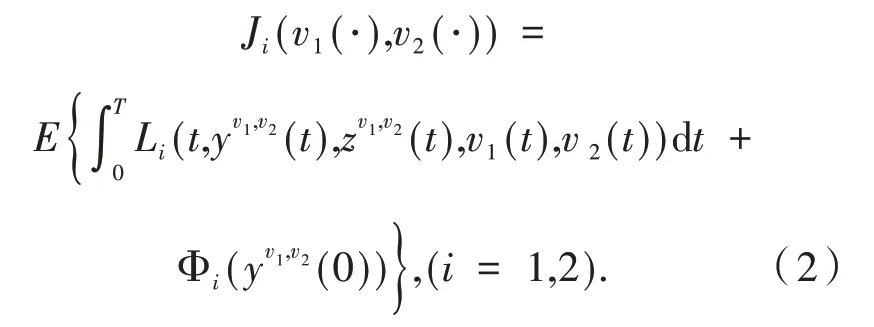
给出下列假设：

（A1）存在常数c> 0 和0 <σ< 1 对于任意的 (ω,t)∈Ω×[0,T]，(y1,z1,u1)，(y2,z2,u2)∈Rn×Rn×d× Rk，则有

（A2）f和g关于(y,z,v1,v2)是连续可微的，且f和g关于(y,z,v1,v2)的偏导数是一致有界的.

（A3）Li对于(y,z,v1,v2)是连续可微的，Φi对于y是连续可微的，且存在正常数C使得偏导数Liy，Liz，Liv1，Liv2有界.

1.3 主要引理

引理1［10］假设（A1）～（A2）成立，对于给定u(·) ∈U(0,T)，存在唯一解满足等式（1），其中(y(·),z(·))=(y(·,u(·)),z(·,u(·)))∈S2(0,T,Rn) ×M2(0,T,Rn×d).

引理2 假设α∈S2(0,T;Rn)，β∈M2(0,T;Rn)，γ∈M2(0,T; Rn× Rm)，δ∈M2(0,T; Rn× Rd)，则有

一般来说ψ∈C2(Rn)，那么

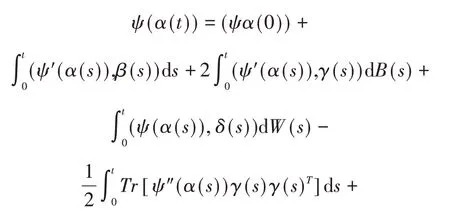
引理3［11］假设（A1）～（A2）成立，设，则有：

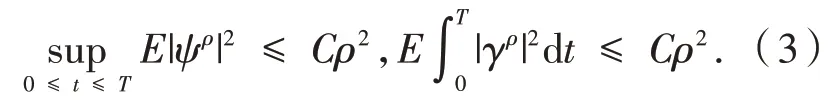
引理4［11］假设（A2）成立，设

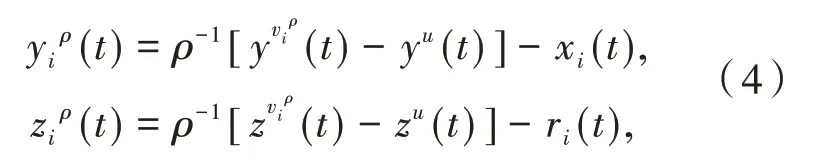
则有：

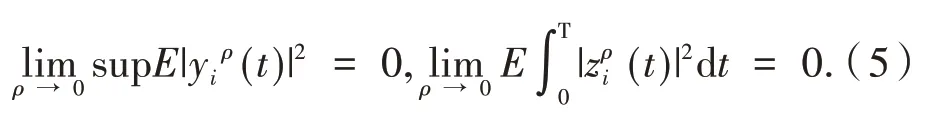
2 主要结果

假设控制双方都想选择最优的容许控制vi(·)(i=1,2)来优化自己的价值泛函，即寻找容许控制(v1(·),v2(·)) ∈U1×U2使其满足：

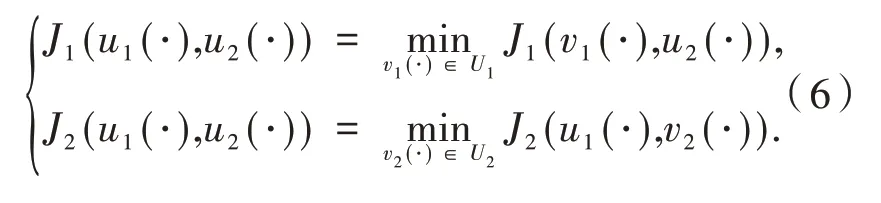
如果可以得到满足式（6）的容许控制(u1(·),u2(·))，则它被称为一个纳什均衡点.

此时系统相应的变分方程可以写成：

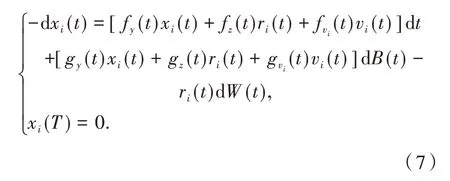
定理1 假设（A2）和（A3）成立，则有：

其中：Liβ(t)=Liβ(t,yu1,u2(t),zu1,u2(t),u1(t),u2(t))，β=y,z,v1,v2,(i=1,2).

证明 对于任意的v1(·) ∈U1,v2(·) ∈U2，由式（2）和式（6）可得

即

继而可得：

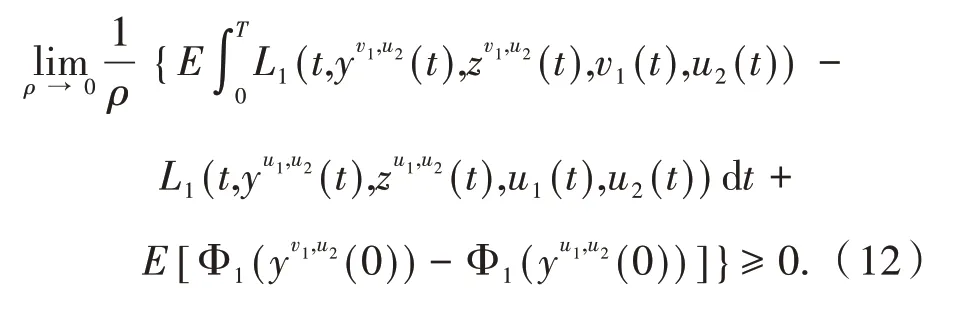
由不等式（11）的第一项推导可得：

根据引理4，可推得：

类似地，由不等式（11）的第二项可推得：

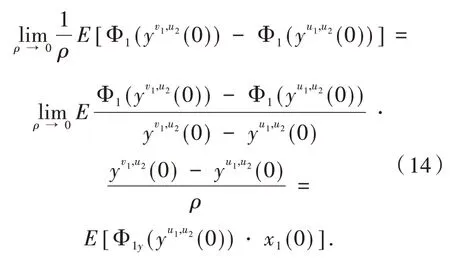
同理，可从不等式（9）中推出i=2 的情况，结合i=1 和i=2，定理证毕.

定义哈密顿函数如下：

对应系统，定义它的伴随方程，系统的伴随方程形式如下：

其中：Liβ(t)=Liβ(t,yu1,u2(t),zu1,u2(t),u1(t),u2(t)),β=y,z.

哈密顿形式的伴随方程如下：

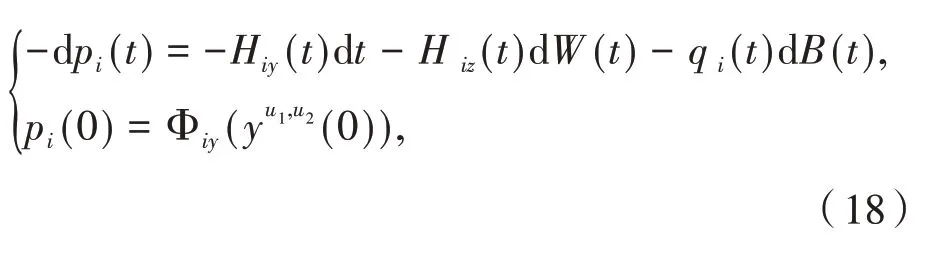
其中：Hi(t)=H(t,yu1,u2(t),zu1,u2(t),u1(t),u2(t)，pi(t)，qi(t))，Hiy(t)、Hiz(t)表示对y和z的偏导数.

定理2 假设（A2）和（A3）成立，对于任意的(v1,v2) ∈U1×U2，假设(u1(·),u2(·))是一个纳什均衡点，且(yu1,u2(·),zu1,u2(·))是对应的最优轨迹，则有：

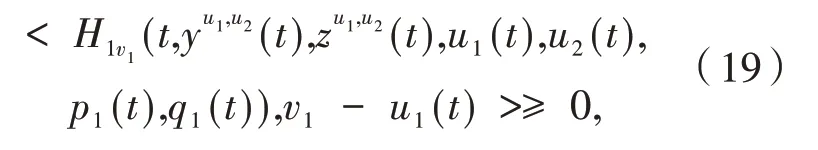
及

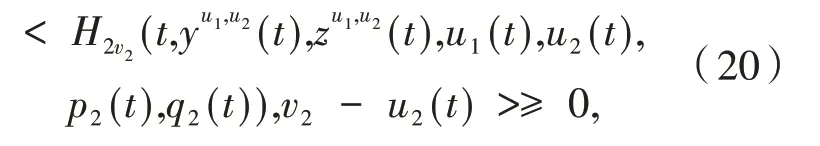
其中：(pi(·),qi(·))是伴随方程（18）的唯一解.

证明 对xi(t),pi(t)应用伊藤公式，可得：

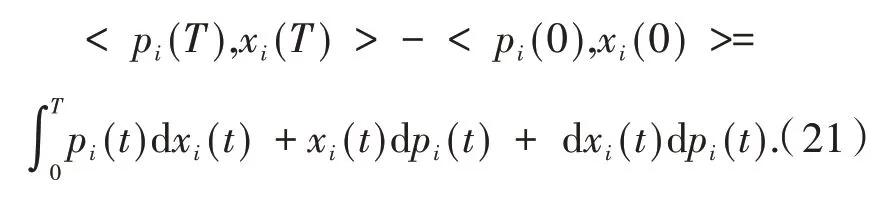
取期望并计算，可得：

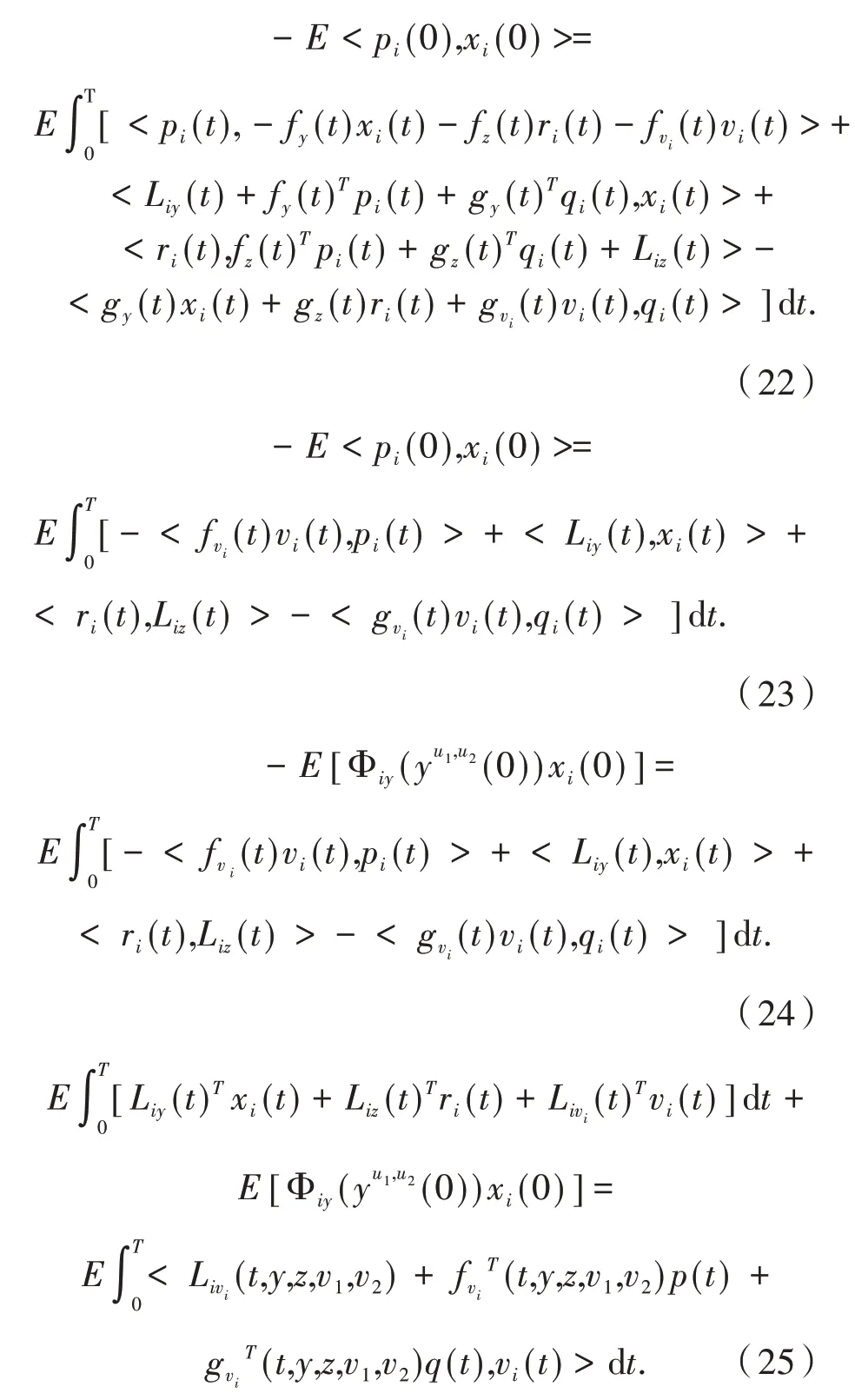
由定理1，可以得到：

对于任意满足v1(·) +u1(·) ∈U1的v1(·)不等式（26）成立.如果假设v1(s) +u1(s)=ϑ(s)，s∈[t,t+ε]，且v1(s) +u1(s)=u1(s),s∉[t,t+ε]，那么可从不等式（26）推出：

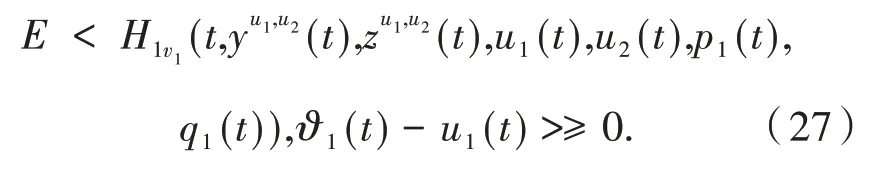
假设ω(t)=v1IA+u1(t)IcA，∀v1∈U1，A∈ℱt，其中IA是集合上A的示性函数且ω(·)是一个容许控制，通过将ω(·)代入不等式（27），可以推得：

对任意的A∈ℱt，不等式（28）都成立，则有：

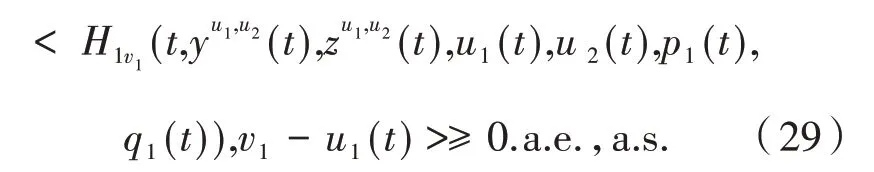
类似地，可推得：

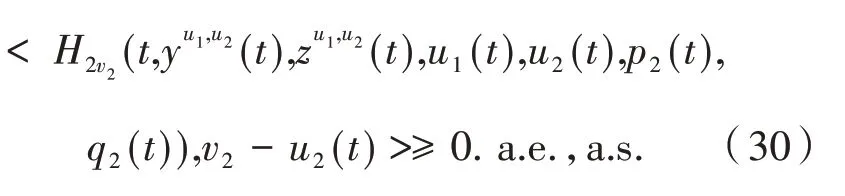
3 结语

自1994年Pardoux 和彭实戈教授给出倒向重随机微分方程以来，讨论由倒向重随机微分方程驱动的控制问题成为人们研究的热点.本文探讨了由倒向重随机微分方程刻画的非零和微分对策问题，在此类问题的研究中，系统的伴随方程是研究的关键，该文利用伴随方程的解刻画了纳什均衡点存在的必要条件，此结果类似于随机最优控制问题的最大值原理.然而由于伴随方程结构的复杂性，关于其解的形式成为研究的难点，将在后续的工作中对此类问题做进一步探讨.