基于多机器学习算法耦合的空气质量数值预报订正方法研究及应用

肖 宇

上海市环境监测中心，上海 200030

大气环境污染已经对公众的健康造成了严重影响[1]，因此发展各类统计学模型对污染物浓度进行预测至关重要.空气质量模型能够综合考虑污染物排放、气象条件和物理化学反应等，是目前最为主流的预测空气质量的手段[2-4].但是，空气质量模式对初始条件和外在强迫的依赖造成了模型的不确定性，大气运动的非线性特征决定了无论来自初始场还是来自模式本身极小的误差在模式积分过程中都将被放大[5].自从混沌理论和大气的非线性本质提出后，Epstein和Lorenz提出了集合预报的思想和方法[6-7]，成为大气科学领域的重要研究方向[8].

近年来，多数研究着重利用机器学习相关方法构建新的预报模型，根据输入气象数据和排放清单对NO2、PM2.5和O3浓度进行预报[9-10]，较少将机器学习方法作为模式结果订正的手段.目前用于预报结果订正的机器学习方法中，研究较多的主要包括神经网络、支持向量机、岭回归、随机森林、长短期记忆网络等.研究发现，BP神经网络对污染物浓度预测具有较好的订正效果[11]；支持向量机算法较多元线性回归法对O3预报准确度更高[12]；门晓磊等[13]利用岭回归、随机森林和深度学习3种机器学习算法对多模式气温进行集合预报，发现在短期预报时深度学习算法的订正效果更好，在中后期预报时岭回归的订正效果略好.极端随机树和梯度提升回归树算法对CMAQ的预报也有较好的订正效果，且其对NO2和O3的优化效果最为明显[14].此外，岭回归比最优化集合预测算法在预测精度和稳定性上均有所提升[15].随机森林对PM2.5优化效果显著，支持向量机对O3的优化效果最理想[16].

基于机器学习的空气质量预测方法主要在欧洲和美国使用，虽在中国起步较晚但近年来发展迅速.结合多个预测器的集成学习算法主要用于污染评估，神经网络和支持向量机等机器学习算法则主要用于空气质量预测[17-18].因此，为了提高机器学习算法对污染物的预报效果，需要考虑对常规污染物均有较好订正效果的单机器学习算法，同时结合各机器学习算法自身的优点，在空间和时间上进行耦合.因此，该研究基于随机森林、极端随机树、梯度提升回归树和BP神经网络4种算法各自的特点进行时空耦合，从而建立一种新的多模式集合预报订正算法(简称“ET-BPNN算法”)，提高了对污染物浓度及变化趋势的预报准确率，以期为重大活动提供技术保障，为管理决策提供重要的理论依据.

1 材料与方法

1.1 数据来源及研究区域

该研究单模式数据源自长三角区域空气质量预报多模式集合预报系统，模式区域的中心经纬度为105°E、36°N，第一区域取东亚地区，水平分辨率为27 km，水平网格点数为240×200；第二区域为中国东南沿海地区，水平分辨率为9 km，水平网格点数为238×223；第三区域取长江下游地区，水平分辨率为3 km，水平网格点数为223×202. 4个空气质量模型分别为CMAQ、CAMx、NAQPMS和WRFChem，模式中采用的参数化方案分别为CBMZ、RADMS、CB05和CB05，排放模型SMOKE为集合系统提供同样区域设置的3层网格化排放源.气象模式为WRF，初始和边界条件取自NOAA(National Oceanic and Atmospheric Administration)的全球预报气象场GFS(Global Forecasting System)数据集.观测资料来自上海市10个国控点的实时观测数据.

该研究中使用的模式资料为长三角区域空气质量预报系统中CAMx、CMAQ、NAQPMS以及WRFChem每日20:00起报的上海市未来7 d逐小时数据，优化的污染物为NO2、O3、PM2.5和PM10，优化的预报时效为24、48、72和96 h.为了排除新冠肺炎疫情的影响，同时考虑季节变化，该研究选取2018年3月1日−2019年2月28日一个完整年作为研究时段.

1.2 算法简介

随机森林算法.随机森林算法是由Leo Breiman和Adele Cutler发展推论出的，该算法从原始数据集中随机地抽取m个子样本，并且在训练每个基学习器时随机地选取k个特征，从中选择最优特征来切分节点，从而进一步降低模型的方差，且不容易出现过拟合现象[19].模型中弱学习器的最大迭代次数n_estimators的选取较为重要，n_estimators越大模拟效果越好，但需要的计算量和内存也越大，训练时间也会延长，为综合平衡预报效果和训练时长，同时结合样本量，该研究中该参数取值100.

极端随机树算法.极端随机树算法是随机森林算法的一个变种，基本原理与随机森林算法类似，仅在采样方式和特征值划分方式上有区别.在采样方式上，随机森林算法采用的是bootstrap，极端随机树算法采用的是原始训练集；在特征值划分方式上，随机森林算法会选择最优特征值作为划分点，极端随机树算法会随机选择一个特征值来划分决策树.

梯度提升回归树算法.梯度提升回归树算法是集成学习的一个重要算法，在被Friedman提出之初与支持向量机算法一起被认为是泛化能力较强的算法，其核心在于每棵树是从先前所有树的残差中来学习.梯度提升回归树算法利用当前模型中损失函数的负梯度值作为残差的近似值，进而拟合一棵回归树.梯度提升回归树算法具有三点优势，分别为可以自然地处理混合类型的数据、预测能力较强以及对异常值的鲁棒性强[20].

BP神经网络算法.BP神经网络算法在1986年由Rumelhart和McClelland首次提出[21]，其输出结果采用前向传播，误差采用反向(back propagation)传播方式进行，是目前应用最广泛的神经网络.BP神经网络包含一个输入层、一个或多个隐含层以及一个输出层，每一层可以有多个神经元.张恒德等[22]对BPNN(反向神经网络)算法中不同隐含层节点数和不同训练函数进行了对比分析，发现隐含层节点数和训练函数分别取10和trainbr (贝叶斯归一化法)时预报效果最好.该研究中激活函数选为softmax，该函数可得到每个模式对污染物浓度预报值与观测值最为接近的概率，最终通过加权平均的方法得到结果.

1.3 研究思路

随机森林、极端随机树和梯度提升回归树均是以决策树为基模型的集成学习算法，具有较大的解释度，同时这类算法适用于类别丰富且存在缺失的数据集.相比而言，神经网络算法对数据集整洁程度要求较高，需要更为严苛的前期准备工作，同时神经网络算法在调参上也更为灵活多变.因此，该研究结合两类机器学习算法的特点，主要优化思路如图1所示.首先，利用以随机森林、极端随机树、梯度提升回归树为代表的集成决策树算法，融入大量、多类源数据进行第一次优化，得到优化后的污染物小时预报值；训练结果进入基于均方根误差的择优选择器，选取3种决策树算法中优化效果最好的算法，再利用BP神经网络算法对数据集进行二次优化，此时输入数据规范且整洁，更有利于BP神经网络算法的调参优化；最终得到单个输入向量的权重，通过加权平均获得订正结果，称为多模式集合预报订正算法(Ensemble Tree-Back Propagation Neural Network，简称“ET-BPNN算法”).

图1 ET-BPNN算法运行流程Fig.1 Running process of ET-BPNN algorithm

利用随机森林、极端随机树和梯度提升回归树算法对4个单模式预测的4项常规污染物浓度进行第一次优化过程中，综合考虑单模式多尺度的污染物浓度预报数据、影响污染物浓度的WRF气象因子预报数据(包括2 m温度、2 m相对湿度、10 m风速、10 m风向、气压和小时累计降水量)以及污染物浓度观测数据.滚动订正预报的运作流程如图2所示，在训练阶段，设当日时间为t，考虑到气象场和污染场的时间连续性，训练时长选取15 d，即用前15 d〔即(t−14)d至t时段〕的逐小时数据作为训练样本，其为8(8类变量)×360(小时数)的矩阵，对应的逐小时观测污染物浓度数据作为测试样本，其为1×24(小时数)的矩阵，训练样本和测试样本为图2中橙色方框所示的数据集，分别利用随机森林、极端随机树和梯度提升回归树进行建模；在预报阶段，利用训练时段的建模，输入(t+1)d的逐小时预报数据，即可得到优化后的单模式污染物浓度预报数据(图2中蓝色方框所示的数据集).

图2 ET-BPNN算法所用数据集(以PM 2.5为例)Fig.2 Diagram of data set used in ET-BPNN algorithm (taking PM 2.5 as an example)

在利用BP神经网络进行二次优化过程中，通过计算均方根误差的最小值得出随机森林、极端随机树和梯度提升回归树中预报效果最优的结果集，该数据集中包含4个不同模式和3个不同模拟区域，共12个输入向量，输入BP神经网络进行集合优化.经过softmax算法，得到每个模式与观测最为接近的概率(∅i).因此，最终的预报值为各单模式优化结果的加权平均(C)，计算公式：

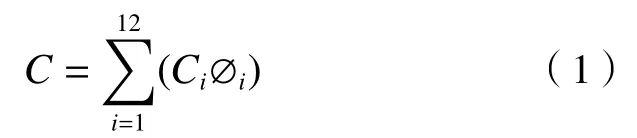
式中：Ci为第i个输入向量的模拟浓度，μg/m3，其中i=1,2,...,12；∅i为经过BP神经网络算法得到的该输入向量对应的概率.

2 结果与讨论

2.1 ET-BPNN算法整体优化效果评估

4个空气质量数值预报模式(CMAQ、CAMx、NAQPMS和WRFChem)以及经模式集合平均算法及ET-BPNN算法优化后的各项污染物小时浓度预报值与观测值的统计学指标如表1所示.由表1可见，ET-BPNN算法对单模式的预报效果有明显改进，以预报效果较好的NAQPMS模式为例，经ET-BPNN算法优化后NO2、O3、PM2.5和PM10浓度预报值与观测值之间的相关系数分别提高了60.6%、41.6%、43.0%和91.4%，均方根误差分别减小了51.9%、60.1%、63.0%和60.0%，均一化标准差分别降低了99.5%、105.3%、97.8%和106.7%，平均相对误差分别降低了39.9%、62.8%、44.8%和50.0%.

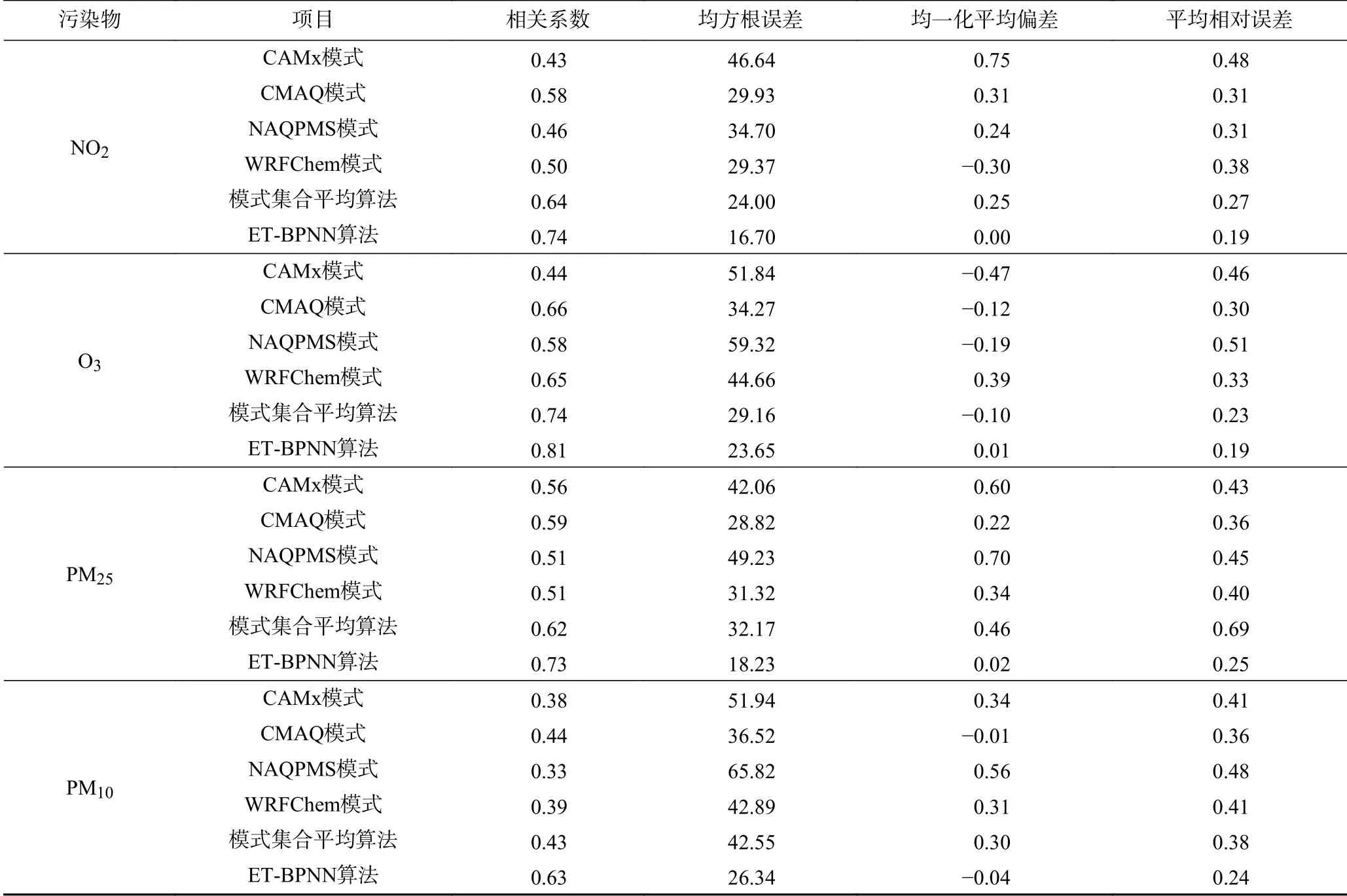
表1 单模式、模式集合平均算法、ET-BPNN算法预报效果对比Table1 Comparisonsof forecasting results of single models,ensemble mean and ET-BPNN

经模式集合平均算法优化后的预报效果较单模式有所提升，与NAQPMS单模式预报结果相比，经模式集合平均算法优化后NO2、O3、PM2.5和PM10浓度预报值与观测值之间的均方根误差分别减小了30.8%、50.8%、34.7%和35.4%.与模式集合平均算法相比较，ET-BPNN算法的优化效果更好，经ET-BPNN算法优化后，NO2、O3、PM2.5和PM10浓度预报值与观测值之间的相关系数分别提高了15.6%、9.5%、17.7%和46.5%，均方根误差分别减小了30.4%、18.9%、43.3%和38.1%，均一化标准差分别降低了100.0%、110.0%、95.7%和113.3%，平均相对误差分别降低了29.6%、17.4%、63.8%和36.8%.

总体而言，ET-BPNN算法能够使模式预报数据在变化趋势和绝对值上与实况更为接近.在数值偏差上，ET-BPNN算法对PM2.5和O3的优化效果最为明显.目前，PM2.5和O3已成为全球最为关注的两种污染物，ET-BPNN算法对二者预报效果的明显改进为污染预报预警和精准管控提供了有力的技术支撑.

由图3可见，经ET-BPNN算法优化后的预报效果较单模式和模式集合平均算法均有明显提升.在4种污染物中，经ET-BPNN算法优化后O3浓度预报值与观测值的相关系数最高，达0.82，标准化偏差仅为0.85；对于PM2.5浓度而言，其在CMAQ单模式中预报效果最为突出，经ET-BPNN算法优化后，预报值与观测值在变化特征和绝对值上与观测值更为接近，相关系数由0.59提至0.73.与模式集合平均算法相比，ET-BPNN算法对固态污染物的优化效果略优于气态污染物，ET-BPNN算法使NO2、O3、PM2.5和PM10四种污染物预报结果的标准化偏差较优化前分别降低了24.0%、4.4%、38.3和41.0%.

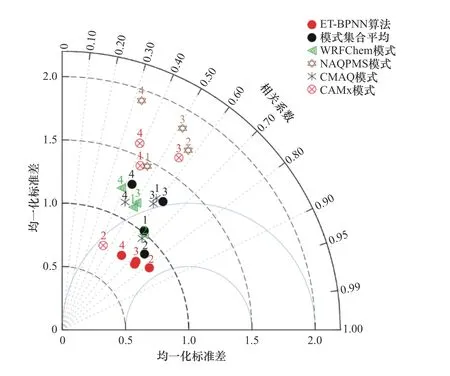
图3 单模式、模式集合平均算法和ET-BPNN算法预报效果评估的泰勒图Fig.3 Forecasting assessment Taylor diagram of the single model,ensemblemean and the ET-BPNN

2.2 ET-BPNN算法在不同预报时效和不同季节的优化效果评估

自2013年起，中国相继发生了数次大范围和长时间的空气污染事件，自此社会对于PM2.5污染的关注程度日益升高[23].ET-BPNN算法在不同季节和不同预报时效上的优化效果如图4、5所示，样本点为上海市10个国控站点.对不同季节而言，ET-BPNN算法在较易发生污染的秋冬季对PM2.5的预报具有明显的优化效果；此外，该算法明显缩小了不同站点之间的预报偏差，具有较好的鲁棒性(即机器学习算法在数据变化时的稳定性).对不同预报时效而言，随着预报时效的增加，单模式的预报偏差逐渐增大，通过ET-BPNN算法优化后不同预报时效之间的偏差明显减小，较大地提高了预报的时效稳定性；同样地，ET-BPNN算法提高了不同站点的预报稳定性，表明该算法具有较强的泛化能力(即机器学习算法对新样本的适应能力).

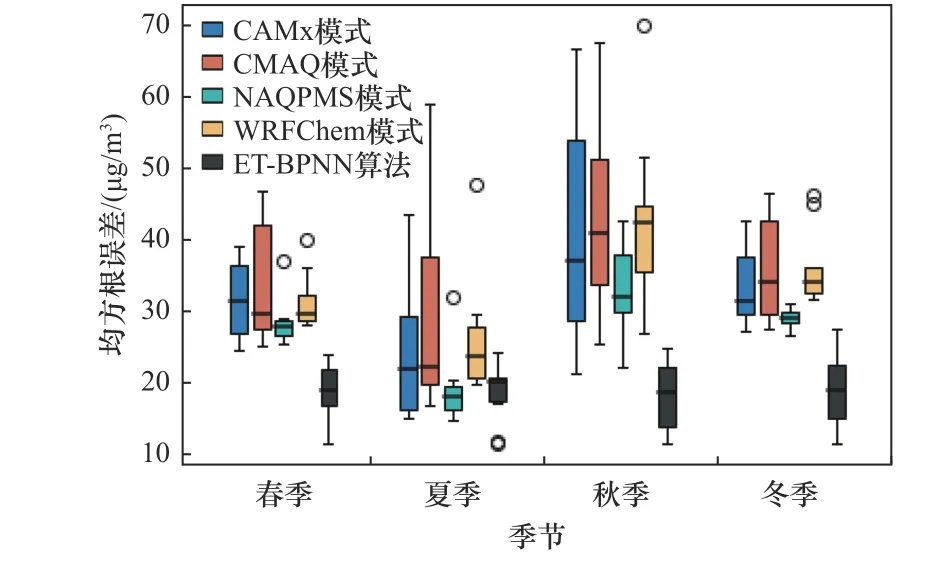
图4 单模式和ET-BPNN算法在不同季节模拟的均方根误差盒须图Fig.4 RMSE distribution of four models and the ET-BPNN in four seasons

2.3 ET-BPNN算法对污染过程的预报订正效果评估

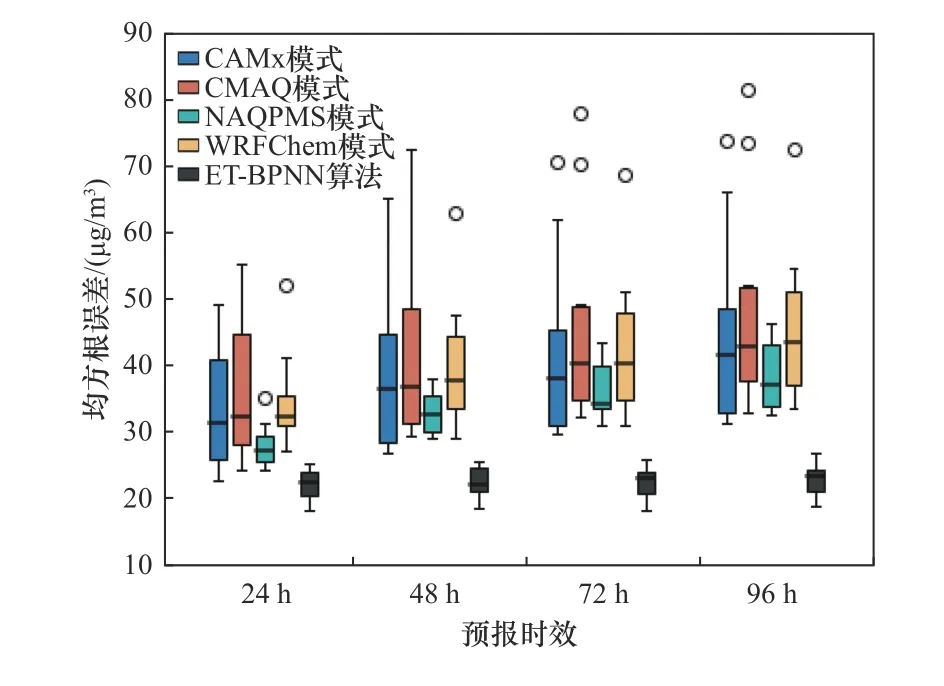
图5 单模式和ET-BPNN算法在不同预报时效模拟的均方根误差盒须图Fig.5 RMSE distribution of four models and the ET-BPNN in different forecasting time

在该研究时段上海市出现了多次O3污染过程，集中在2018年4−10月，其中，轻度污染24 d，中度污染3 d.选取包含轻度和中度污染过程的2018年7月27−28日(其中，27日为中度污染，28日为轻度污染)进行分析，在此次污染过程中实测O3小时浓度最高值为294μg/m3，ET-BPNN算法和模式集合平均算法预报的当日O3小时浓度最高值分别为209和124μg/m3，可见ET-BPNN算法较模式集合平均算法对O3峰值浓度有更好的预报效果.与模式集合平均算法相比，ET-BPNN算法对此次污染过程预报结果进行订正后，均方根误降低了30.3%.对PM2.5而言，在研究时段共出现25个轻度污染日，2个中度污染日，集中在2018年11月−2019年2月. 选取包含PM2.5轻度和中度污染过程的2019年2月23−25日进行分析(其中，23日为中度污染，24−25日为轻度污染)，实测PM2.5小时浓度最高值为159μg/m3，ET-BPNN算法和模式集合平均算法预报的当日PM2.5小时浓度最高值分别为100和78μg/m3.与模式集合平均算法相比，ET-BPNN算法对此次污染过程预报结果进行订正后，均方根误降低了20.6%.

分析ET-BPNN算法对污染时段O3-8 h浓度和PM2.5浓度日均值的模拟优化情况.由图6可见，对O3而言，单模式预报结果出现一定程度的高估，经ET-BPNN算法优化后的预报值能够更好地把握污染过程，对污染物峰值浓度的预报也较模式集合平均算法更准确，二者的预报平均误差分别为32.5和48.9 μg/m3，平均误差率分别为27.1%和40.8%.由图7可见，对PM2.5而言，单模式在污染日的预报效果较非污染日差，经ET-BPNN算法优化后的预报值在变化趋势和绝对值上都与观测值最为接近，与模式集合平均算法相比，ET-BPNN算法在污染日的预报效果更优，而模式集合平均算法易出现高估或低估的情况，二者的预报平均误差分别为16.0和22.2μg/m3，平均误差率分别为37.5%和52.1%.

图6 2018年4—10月O3-8 h浓度的观测值、ET-BPNN算法预报值、模式集合平均算法预报值以及单模式预报值范围的时间序列Fig.6 Timeseries of observed daily O3-8 h concentration and forecasting daily O3-8 h concentration optimized by ET-BPNN algorithm and ensembleaverage algorithm from April to October,2018

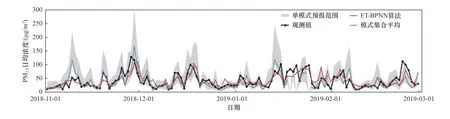
图7 2018年11月—2019年2月PM 2.5浓度的观测值、ET-BPNN算法预报值、模式集合平均算法预报值以及单模式预报值范围的时间序列Fig.7 Time seriesof observed daily PM 2.5 concentration and forecasting daily PM 2.5 concentration optimized by ET-BPNN algorithm and ensembleaverage algorithm from November 2018 to February 2019

4个单模式、模式集合平均算法以及ET-BPNN算法的污染物(NO2、O3、PM2.5和PM10)小时浓度预报值与实测值的均方根误差月分布热力图如图8所示.由图8可见，单模式以及ET-BPNN算法和模式集合平均算法均对NO2的预报效果较优，PM2.5次之，对O3和PM10的预报效果相对较差.由于PM10污染主要是由北方沙尘传输引起，而未包含沙尘预报模块的空气质量模型仅能通过数据同化对初始场和边界场进行更新，因此对沙尘的预报能力较弱.对于出现O3污染的4−10月，单模式模拟效果预报效果均较差，经ET-BPNN算法优化后预报效果较模式集合平均算法更好，在9、10月EP-BPNN算法使O3浓度预报值与实测值的均方根误差分别较模式集合平均算法降低了27.2%和33.9%.在出现PM2.5污染的2018年11月−2019年2月，对4个单模式而言，CMAQ和WRFChem的预报效果较CAMx和NAQPMS好，ET-BPNN算法优化效果明显，2018年11月、12月和2019年1月、2月EP-BPNN算法使PM2.5浓度预报值与实测值的均方根误差较模式集合平均算法分别降低了57.7%、31.3%、30.8%和0.3%.对全年各月份而言，ET-BPNN算法较模式集合平均算法对固态污染物预报的优化效果比气态污染物更好，使PM2.5、PM10、NO2和O3小时浓度预报值与实测值的均方根误差分别减少了40.7%、38.7%、28.8%和17.2%.

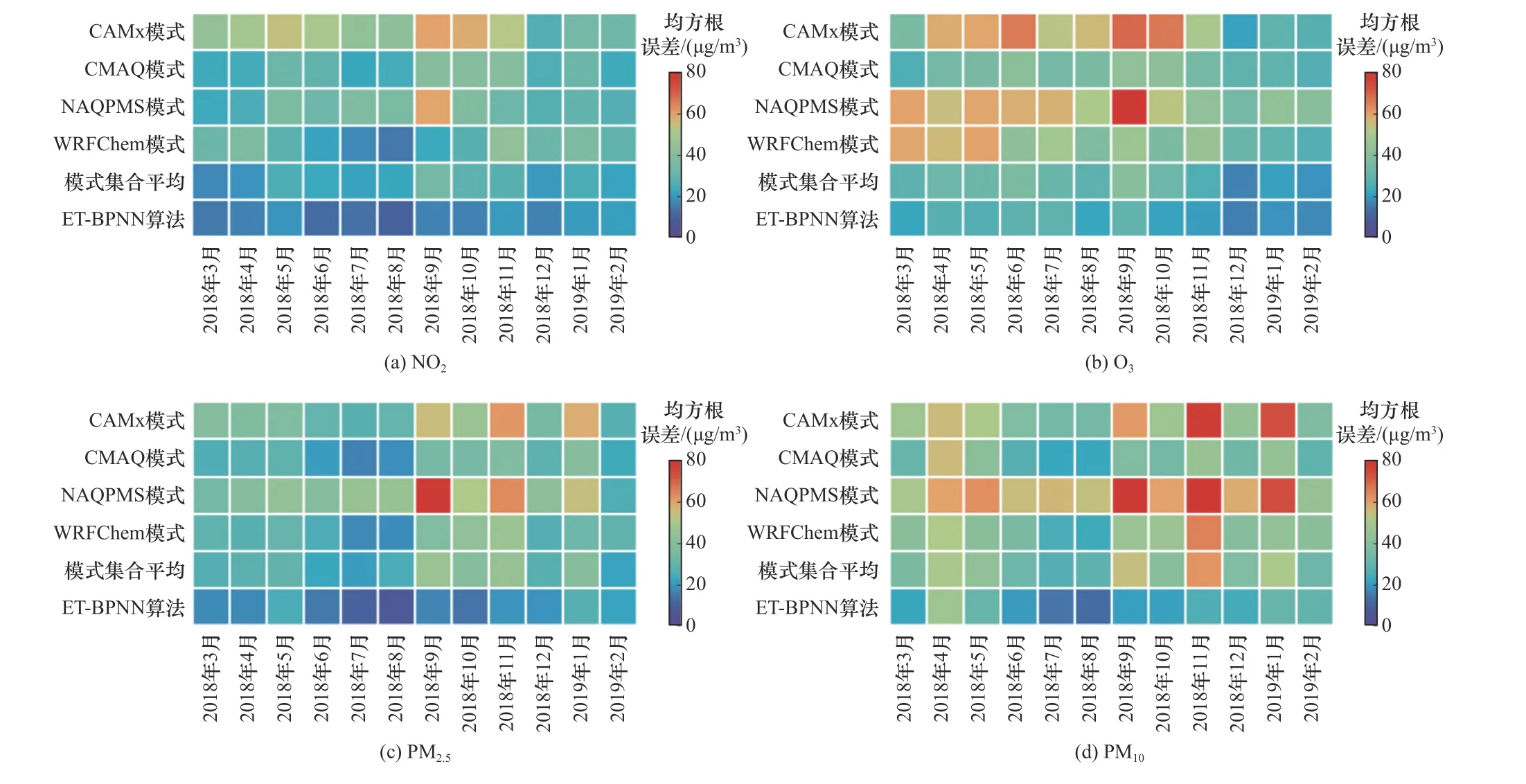
图8 单模式和两种集合算法的4种污染物小时浓度预报值与实测值的均方根误差月分布热力图Fig.8 Monthly RMSE of four models and two ensemble algorithms between the hourly forecasting valuesand hourly observation values of four pollutants

2.4 适应性分析

ET-BPNN算法的适用范围较广，该研究中建立的ET-BPNN算法是对4种污染物的预报小时浓度数据进行优化订正，但该算法也可用于对不同站点、不同预报时效和不同污染物的预报订正.此外，该算法也可用于气象领域，对不同气象因子的预报效果进行订正.在利用该算法进行优化时，可引入对优化目标有影响的特征因子，特征因子的合理选取和前期清洗对订正效果有较大影响，许博等[24]利用随机森林算法探究了排放源、大气氧化能力、气象条件等多种驱动因素对PM2.5浓度的影响.Jiang等[25]基于粗糙集理论进行数据清洗后再利用BPNN算法对空气质量预测，取得了较好的效果.

由于大部分集合预报的缺陷在于统计方法常常对平均状态的预报改进显著，但会漏掉极端值的预报[26]，对于日变化较大的污染物(如O3)集合算法在这方面的缺陷则显现出来[27].Chaiyakhan等[28]先利用K-mean方法对O3浓度先进行聚类，然后利用支持向量机对小时地面O3浓度进行预报，达到较好的预报效果.类似地，结合基于遗传优化的BPNN算法和支持向量机算法对北京市O3浓度进行预报也得到了较好的效果[29].Mallet等[30]研究发现，连续聚类的机器学习集合预报算法对O3浓度的业务预报具有较大的改进作用.因此，在对有规律日变化的污染物进行预报订正时，采用聚类方法对数据进行前处理，或许可以有效地改善预报效果.

3 结论

a)ET-BPNN算法对单模式的预报效果有明显改进，以预报效果较好的NAQPMS模式为例，经过ET-BPNN算法优化后NO2、O3、PM2.5和PM10浓度预报值与观测值之间的均方根误差分别减小了51.9%、60.1%、63.0%和60.0%；与模式集合平均算法相比较，经ET-BPNN算法优化后NO2、O3、PM2.5和PM10浓度预报值与观测值之间的均方根误差分别减小了30.4%、18.9%、43.3%和38.1%.ET-BPNN算法能够使模式预报数据在变化趋势和绝对值上均与实况更为接近，综合考虑所有单模式的预报效果，该优化算法对NO2的优化效果最为明显.

b) 对不同季节PM2.5预报效果改进方面，ET-BPNN算法在较易发生污染的秋冬季对PM2.5的预报具有明显的优化效果；此外，该算法明显缩小了不同站点的预报偏差，具有较好的鲁棒性.对不同预报时效的PM2.5预报效果改进方面，经ET-BPNN算法优化后不同预报时效之间的偏差明显减小，较大地提高了预报的时效稳定性.

c)在污染过程模拟方面，对O3-8 h浓度而言，单模式预报结果有一定程度的高估，经ET-BPNN算法优化后的预报值能够更好地把握污染过程，对污染物峰值浓度的预报也较模式集合平均算法更准确，二者的预报平均误差分别为32.5和48.9μg/m3.对PM2.5浓度而言，与模式集合平均算法相比较，ET-BPNN算法在污染日的预报效果更优，而模式集合平均算法容易出现高估或低估，二者的预报平均误差分别为16.0和22.2μg/m3.ET-BPNN算法较模式集合平均算法对固态污染物的优化效果比气态污染物更明显，PM2.5、PM10、NO2和O3小时浓度预报值与实测值的均方根误差分别减少了40.7%、38.7%、28.8%和17.2%.